No CrossRef data available.
Article contents
A note on some compound poisson distributions
Published online by Cambridge University Press: 29 August 2014
Extract
At the Lundberg Symposium, Stockholm 1968 Jung and Lundberg presented a report on similar problems as those treated in this note, and to the Astin colloquium, Berlin 1968 the present author presented a report with the same title as this note, where some of the results in the first-mentioned report were commented upon. Jung and Lundberg kindly discussed the topic here concerned with the present author some time after the colloquium. On account of this discussion, the present author withdrew his report from the publication in its original form. The following context is a revision and a completion of the author's report to the colloquium.
Let τ be a parameter measured on its original, absolute scale, and let 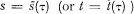 be the same parameter measured on an operational scale with respect to the probability distribution
be the same parameter measured on an operational scale with respect to the probability distribution 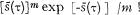 (or the corresponding for t). The parameter will often be referred to as “time”, which does not imply a restriction of the theory to proper time parameters.
(or the corresponding for t). The parameter will often be referred to as “time”, which does not imply a restriction of the theory to proper time parameters.
A random function X(s) is said to be distributed in a cPd i.w.s. (compound Poisson distribution in the wide sense), if the distribution function of X(s) for every fixed parameter point (s, τ) in a finite or infinite domaine of the parametric space as a function of τ can be written in the following general form
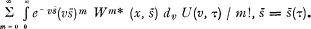
where the asterisk power m*, here and throughout this note, is taken to mean, for m ˃ O, the m times iterated convolution of the distribution function with itself, and, for m = o, unity. W(x, s)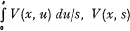 being the conditional distribution function of the size of one change in X(s) relative to the hypothesis that the change has occurred at s, here abbreviated to the change distribution. U(ν, τ) is a distribution function, called the structure function. In the general case V(x, s) and U(ν, τ) may depend on s and τ respectively. If, particularly, these functions are supposed to be independent of the parameter, they will be denoted V(x), U(ν) respectively. In the particular case, where V(x) = ε(ν—c1), c1 being an arbitrary but fixed constant and ε(ξ), here, and in the following context, the unity distribution equal to zero for negative values, and to unity for non-negative values of ξ, the cPd is said to be elementary and, in the opposite case, non-elementary. In the elementary case the distribution of X(s) is defined by the integral appearing in (Ia) with x = c1, so that W(x, s) = W(x) = I.
being the conditional distribution function of the size of one change in X(s) relative to the hypothesis that the change has occurred at s, here abbreviated to the change distribution. U(ν, τ) is a distribution function, called the structure function. In the general case V(x, s) and U(ν, τ) may depend on s and τ respectively. If, particularly, these functions are supposed to be independent of the parameter, they will be denoted V(x), U(ν) respectively. In the particular case, where V(x) = ε(ν—c1), c1 being an arbitrary but fixed constant and ε(ξ), here, and in the following context, the unity distribution equal to zero for negative values, and to unity for non-negative values of ξ, the cPd is said to be elementary and, in the opposite case, non-elementary. In the elementary case the distribution of X(s) is defined by the integral appearing in (Ia) with x = c1, so that W(x, s) = W(x) = I.
- Type
- Research Article
- Information
- Copyright
- Copyright © International Actuarial Association 1971




