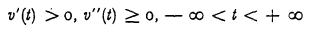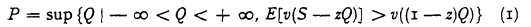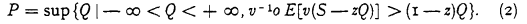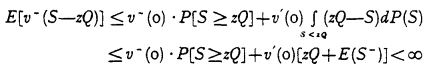Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bernhardt, Rainer
and
Endres, Jürgen
1979.
Erfahrungstarifierung (experience rating) und getrennte AbrechnungsverbÄnde in der Lebensversicherung.
Blätter der DGVFM,
Vol. 14,
Issue. 2,
p.
200.
Goovaerts, M. J.
and
Vylder, F. De
1979.
A Note on Iterative Premium Calculation Principles.
ASTIN Bulletin,
Vol. 10,
Issue. 3,
p.
325.
De Vylder, F.
and
Goovaerts, M.
1980.
Convexity Inequalities for the Swiss premium.
Blätter der DGVFM,
Vol. 14,
Issue. 3,
p.
427.
Taylor, G. C.
1980.
Probability of ruin with variable premium rate.
Scandinavian Actuarial Journal,
Vol. 1980,
Issue. 2,
p.
57.
Goovaerts, M. J.
1981.
On Ordering and Danger of Claim Frequency Distributions.
ASTIN Bulletin,
Vol. 12,
Issue. 1,
p.
72.
Goovaerts, M. J.
1981.
Some further results on ordering of risks.
Blätter der DGVFM,
Vol. 15,
Issue. 1,
p.
1.
Heilmann, Wolf-Rüdiger
1981.
Improved methods for calculating and estimating maximal stop-loss premiums.
Blätter der DGVFM,
Vol. 15,
Issue. 1,
p.
29.
Haezendonck, J.
and
Goovaerts, M.
1982.
A new premium calculation principle based on Orlicz norms.
Insurance: Mathematics and Economics,
Vol. 1,
Issue. 1,
p.
41.
Taylor, G.C.
1982.
Estimation of outstanding reinsurance recoveries on the basis of incomplete information.
Insurance: Mathematics and Economics,
Vol. 1,
Issue. 1,
p.
3.
Goovaerts, M.J.
De Vylder, F.
and
Haezendonck, J.
1982.
Ordering of risks: a review.
Insurance: Mathematics and Economics,
Vol. 1,
Issue. 2,
p.
131.
Reich, Axel
1984.
Homogeneous Premium Calculation Principles.
ASTIN Bulletin,
Vol. 14,
Issue. 2,
p.
123.
Goovaerts, M. J.
and
Leuven, K. U.
1984.
Premium Calculation in Insurance.
p.
195.
Reich, Axel
1984.
Premium principles and translation invariance.
Insurance: Mathematics and Economics,
Vol. 3,
Issue. 1,
p.
57.
Gerber, Hans U.
1984.
Error bounds for the compound poisson approximation.
Insurance: Mathematics and Economics,
Vol. 3,
Issue. 3,
p.
191.
Mack, Thomas
1984.
Premium Calculation for Deductible Policies with an Aggregate Limit.
ASTIN Bulletin,
Vol. 14,
Issue. 2,
p.
105.
Kremer, Erhard
1984.
Premium Calculation in Insurance.
p.
285.
Taylor, G. C.
1985.
A Heuristic Review of some Ruin Theory Results.
ASTIN Bulletin,
Vol. 15,
Issue. 2,
p.
73.
Reich, Axel
1985.
Eine Charakterisierung des Standardabweichungsprinzips.
Blätter der DGVFM,
Vol. 17,
Issue. 2,
p.
93.
Kaas, R.
and
Goovaerts, M. J.
1986.
Bounds on Stop-Loss Premiums for Compound Distributions.
ASTIN Bulletin,
Vol. 16,
Issue. 1,
p.
13.
Taylor, G.C.
1986.
Discussion of ‘Best bounds for positive distributions with fixed moments’ by R. Kaas and M.J. Goovaerts.
Insurance: Mathematics and Economics,
Vol. 5,
Issue. 1,
p.
93.