No CrossRef data available.
Article contents
COUNTING UNIONS OF SCHREIER SETS
Published online by Cambridge University Press: 27 December 2023
Abstract
A subset of positive integers F is a Schreier set if it is nonempty and 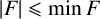 $|F|\leqslant \min F$ (here
$|F|\leqslant \min F$ (here 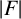 $|F|$ is the cardinality of F). For each positive integer k, we define
$|F|$ is the cardinality of F). For each positive integer k, we define 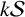 $k\mathcal {S}$ as the collection of all the unions of at most k Schreier sets. Also, for each positive integer n, let
$k\mathcal {S}$ as the collection of all the unions of at most k Schreier sets. Also, for each positive integer n, let 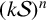 $(k\mathcal {S})^n$ be the collection of all sets in
$(k\mathcal {S})^n$ be the collection of all sets in 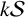 $k\mathcal {S}$ with maximum element equal to n. It is well known that the sequence
$k\mathcal {S}$ with maximum element equal to n. It is well known that the sequence 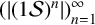 $(|(1\mathcal {S})^n|)_{n=1}^\infty $ is the Fibonacci sequence. In particular, the sequence satisfies a linear recurrence. We show that the sequence
$(|(1\mathcal {S})^n|)_{n=1}^\infty $ is the Fibonacci sequence. In particular, the sequence satisfies a linear recurrence. We show that the sequence 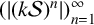 $(|(k\mathcal {S})^n|)_{n=1}^\infty $ satisfies a linear recurrence for every positive k.
$(|(k\mathcal {S})^n|)_{n=1}^\infty $ satisfies a linear recurrence for every positive k.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
J. Hodor is partially supported by a Polish National Science Center grant (BEETHOVEN; UMO-2018/31/G/ST1/03718).





