Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-07T10:06:04.406Z Has data issue: false hasContentIssue false
  • English
  • Français

FIRST EIGENVALUE CHARACTERISATION OF CLIFFORD HYPERSURFACES AND VERONESE SURFACES

Part of: Global differential geometry

Published online by Cambridge University Press:  25 April 2024

PEIYI WU Open the ORCID record for PEIYI WU [Opens in a new window]
PEIYI WU*
Affiliation:
School of Mathematics, Fudan University, Shanghai 200433, PR China
*
e-mail: pwu17@fudan.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a sharp estimate for the first eigenvalue of the Schrödinger operator $L:=-\Delta -\sigma $ which is defined on the closed minimal submanifold 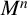$M^{n}$ in the unit sphere 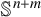$\mathbb {S}^{n+m}$, where 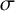$\sigma $ is the square norm of the second fundamental form.

Keywords

minimal submanifoldthe first eigenvalueSchrödinger operator

MSC classification

Primary: 53C24: Rigidity results
Secondary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chen, Q. and Xu, S., ‘Rigidity of compact minimal submanifolds in a unit sphere’, Geom. Dedicata 45(1) (1993), 83–88.CrossRefGoogle Scholar
Chern, S.-S., do Carmo, M. and Kobayashi, S., ‘Minimal submanifolds of a sphere with second fundamental form of constant length’, in: Functional Analysis and Related Fields (ed. Browder, F. E.) (Springer, Berlin–Heidelberg, 1970), 59–75.Google Scholar
Lawson, H. B., ‘Local rigidity theorems for minimal hypersurfaces’, Ann. of Math. (2) 89 (1969), 187–197.CrossRefGoogle Scholar
Li, A.-M. and Li, J., ‘An intrinsic rigidity theorem for minimal submanifolds in a sphere’, Arch. Math. (Basel) 58(6) (1992), 582–594.Google Scholar
Lu, Z., ‘Normal scalar curvature conjecture and its applications’, J. Funct. Anal. 261(5) (2011), 1284–1308.CrossRefGoogle Scholar
Luo, Y., Sun, L. and Yin, J., ‘An optimal pinching theorem of minimal Legendrian submanifolds in the unit sphere’, Calc. Var. Partial Differential Equations 61(5) (2022), 1–18.CrossRefGoogle Scholar
Perdomo, O., ‘First stability eigenvalue characterization of Clifford hypersurfaces’, Proc. Amer. Math. Soc. 130(11) (2002), 3379–3384.CrossRefGoogle Scholar
Shen, Y. B., ‘Curvature and stability for minimal submanifolds’, Sci. Sinica Ser. A 31(7) (1988), 787–797.Google Scholar
Simons, J., ‘Minimal varieties in Riemannian manifolds’, Ann. of Math. (2) 88 (1968), 62–105.CrossRefGoogle Scholar
Wu, C., ‘New characterizations of the Clifford tori and the Veronese surface’, Arch. Math. (Basel) 61 (1993), 277–284.CrossRefGoogle Scholar
Yin, J. and Qi, X., ‘Sharp estimates for the first eigenvalue of Schrödinger operator in the unit sphere’, Proc. Amer. Math. Soc. 150(7) (2022), 3087–3101.CrossRefGoogle Scholar