No CrossRef data available.
Article contents
ON THE DIVISIBILITY OF SUMS OF q-SUPER CATALAN NUMBERS
Published online by Cambridge University Press: 15 May 2023
Abstract
The integrality of the numbers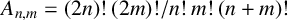 
$A_{n,m}={(2n)!(2m)!}/{n!m!(n+m)!}$ was observed by Catalan as early as 1874 and Gessel named 
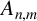$A_{n,m}$ the super Catalan numbers. The positivity of the q-super Catalan numbers (q-analogue of the super Catalan numbers) was investigated by Warnaar and Zudilin [‘A q-rious positivity’, Aequationes Math. 81 (2011), 177–183]. We prove the divisibility of sums of q-super Catalan numbers, which establishes a q-analogue of Apagodu’s congruence involving super Catalan numbers.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The first author was supported by the National Natural Science Foundation of China (grant 12171370).
References
Allen, E. and Gheorghiciuc, I., ‘A weighted interpretation for the super Catalan numbers’, J. Integer Seq. 17 (2014), Article no. 14.10.7.Google Scholar
Apagodu, M., ‘Elementary proof of congruences involving sum of binomial coefficients’, Int. J. Number Theory 14 (2018), 1547–1557.CrossRefGoogle Scholar
Chen, X. and Wang, J., ‘The super Catalan numbers
$S\left(m,m+s\right)$
for
$s\le 4$
’, Preprint, 2012, arXiv:1208.4196.Google Scholar
$S\left(m,m+s\right)$
for
$s\le 4$
’, Preprint, 2012, arXiv:1208.4196.Google ScholarGasper, G. and Rahman, M., Basic Hypergeometric Series, 2nd edn, Encyclopedia of Mathematics and Its Applications, 96 (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Guo, V. J. W., Jouhet, F. and Zeng, J., ‘Factors of alternating sums of products of binomial and
$q$
-binomial coefficients’, Acta Arith. 127 (2007), 17–31.CrossRefGoogle Scholar
$q$
-binomial coefficients’, Acta Arith. 127 (2007), 17–31.CrossRefGoogle ScholarLiu, J.-C., ‘Congruences on sums of super Catalan numbers’, Results Math. 73 (2018), Article no. 140.CrossRefGoogle Scholar
Liu, J.-C., ‘On a congruence involving
$q$
-Catalan numbers’, C. R. Math. Acad. Sci. Paris 358 (2020), 211–215.CrossRefGoogle Scholar
$q$
-Catalan numbers’, C. R. Math. Acad. Sci. Paris 358 (2020), 211–215.CrossRefGoogle ScholarPetkovšek, M., Wilf, H. S. and Zeilberger, D.,
$A=B$
(A.K. Peters, Wellesley, MA, 1996).Google Scholar
$A=B$
(A.K. Peters, Wellesley, MA, 1996).Google ScholarPippenger, N. and Schleich, K., ‘Topological characteristics of random triangulated surfaces’, Random Structures Algorithms 28 (2006), 247–288.CrossRefGoogle Scholar
Stanley, R. P., Enumerative Combinatorics, Vol. 2 (Cambridge University Press, Cambridge, 1999).CrossRefGoogle Scholar
Sun, Z.-W. and Tauraso, R., ‘On some new congruences for binomial coefficients’, Int. J. Number Theory 7 (2011), 645–662.CrossRefGoogle Scholar
Tauraso, R., ‘
$q$
-Analogs of some congruences involving Catalan numbers’, Adv. Appl. Math. 48 (2012), 603–614.CrossRefGoogle Scholar
$q$
-Analogs of some congruences involving Catalan numbers’, Adv. Appl. Math. 48 (2012), 603–614.CrossRefGoogle ScholarVon Szily, K., ‘Üeber die Quadratsummen der Binomialcoefficienten’, Ungar. Ber. 12 (1894), 84–91.Google Scholar
Warnaar, S. O. and Zudilin, W., ‘A
$q$
-rious positivity’, Aequationes Math. 81 (2011), 177–183.CrossRefGoogle Scholar
$q$
-rious positivity’, Aequationes Math. 81 (2011), 177–183.CrossRefGoogle Scholar