Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-12T09:57:26.189Z Has data issue: false hasContentIssue false
  • English
  • Français

RECOVERY OF THE TEMPERATURE DISTRIBUTION IN A MULTILAYER FRACTIONAL DIFFUSION EQUATION

Part of: General theory of linear operators Harmonic analysis in one variable

Published online by Cambridge University Press:  20 February 2019

KHIEU T. TRAN Open the ORCID record for KHIEU T. TRAN [Opens in a new window] ,
LUAN N. TRAN Open the ORCID record for LUAN N. TRAN [Opens in a new window] ,
HONG B. Q. NGUYEN Open the ORCID record for HONG B. Q. NGUYEN [Opens in a new window]  and
KHANH Q. TRA Open the ORCID record for KHANH Q. TRA [Opens in a new window]
KHIEU T. TRAN
Affiliation:
Faculty of Mathematics and Computer Science, University of Science, Vietnam National University Ho Chi Minh City (VNU-HCM), 227 Nguyen Van Cu street, District 5, Ho Chi Minh City, Vietnam Institute for Computational Science and Technology, Ho Chi Minh City, Vietnam email ttkhieu@gmail.com, Khieu.tt@icst.org.vn
LUAN N. TRAN
Affiliation:
Institute for Computational Science and Technology, Ho Chi Minh City, Vietnam email Luan.tn@icst.org.vn
HONG B. Q. NGUYEN
Affiliation:
UFR Mathématiques, Université de Rennes 1, Beaulieu, Bâtiments 22 et 23, 263 avenue du Général Leclerc, 35042 Rennes CEDEX, France email nguyenquanbahong@gmail.com
KHANH Q. TRA*
Affiliation:
Division of Computational Mathematics and Engineering, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Vietnam Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam email traquockhanh@tdtu.edu.vn
*
✉traquockhanh@tdtu.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the inverse boundary value problem for fractional diffusion in a multilayer composite medium. Given data in the right boundary of the second layer, the problem is to recover the temperature distribution in the first layer, which is inaccessible for measurement. The problem is ill-posed and we propose a Fourier spectral approach to achieve Hölder approximations. The convergence analysis is performed in both the 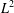$L^{2}$- and 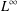$L^{\infty }$-settings.

Keywords

fractional diffusion equationcomposite materialFourier spectral methodill-posed problem

MSC classification

Primary: 47A52: Ill-posed problems, regularization
Secondary: 42A38: Fourier and Fourier-Stieltjes transforms and other transforms of Fourier type
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 344 - 352
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant no. 101.02-2018.312.

References

Fu, C.-L., Xiong, X.-T. and Qian, Z., ‘Fourier regularization for a backward heat equation’, J. Math. Anal. Appl. 331(1) (2007), 472–480.10.1016/j.jmaa.2006.08.040Google Scholar
Iyiola, O. S. and Zaman, F. D., ‘A fractional diffusion equation model for cancer tumor’, AIP Adv. 4(10) (2014), 107–121.Google Scholar
Korbel, J. and Luchko, Y., ‘Modeling of financial processes with a space–time fractional diffusion equation of varying order’, Fract. Calc. Appl. Anal. 19(6) (2016), 1414–1433.Google Scholar
Nguyen, D., Hai, D. and Trong, D. D., ‘The backward problem for a nonlinear Riesz–Feller diffusion equation’, Acta Math. Vietnam. 43(3) (2018), 449–470.Google Scholar
Roberto Evangelista, L. and Kaminski Lenzi, E., Fractional Diffusion Equations and Anomalous Diffusion (Cambridge University Press, Cambridge, 2018).Google Scholar
Tuan, N. H., Ngoc, T. B., Tatar, S. and Long, L. D., ‘Recovery of the solute concentration and dispersion flux in an inhomogeneous time fractional diffusion equation’, J. Comput. Appl. Math. 342 (2018), 96–118.Google Scholar
Xiong, X., Guo, H. and Liu, X., ‘An inverse problem for a fractional diffusion equation’, J. Comput. Appl. Math. 236(17) (2012), 4474–4484.Google Scholar
Xiong, X. T., Shi, W. X. and Hon, Y. C., ‘A one-dimensional inverse problem in composite materials: regularization and error estimates’, Appl. Math. Model. 39(18) (2015), 5480–5494.10.1016/j.apm.2015.01.004Google Scholar
Zheng, G. H. and Wei, T., ‘Spectral regularization method for solving a time-fractional inverse diffusion problem’, Appl. Math. Comput. 218(2) (2011), 396–405.Google Scholar