Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Frappier, C.
1998.
Representation formulas for entire functions of exponential type and generalized bernoulli polynomials.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 64,
Issue. 3,
p.
307.




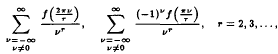
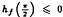 in the first case). These series are expressed in terms of the derivatives of
in the first case). These series are expressed in terms of the derivatives of 