Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-05-31T06:48:26.529Z Has data issue: false hasContentIssue false
  • English
  • Français

TRIPLE-PRODUCT-FREE SETS

Part of: Special aspects of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  06 October 2023

PRECIOUS U. AGIGOR-MIKE Open the ORCID record for PRECIOUS U. AGIGOR-MIKE [Opens in a new window] ,
SARAH B. HART Open the ORCID record for SARAH B. HART [Opens in a new window]  and
MARTIN C. OBI Open the ORCID record for MARTIN C. OBI [Opens in a new window]
PRECIOUS U. AGIGOR-MIKE
Affiliation:
Department of Mathematics, Federal University of Technology, Owerri, Imo state, Nigeria e-mail: precious.agigormike@futo.edu.ng
SARAH B. HART*
Affiliation:
Department of Economics, Mathematics and Statistics, Birkbeck College, University of London, Malet Street, London WC1E 7HX, UK
MARTIN C. OBI
Affiliation:
Department of Mathematics, Federal University of Technology, Owerri, Imo state, Nigeria e-mail: martins.obi@futo.edu.ng
*
e-mail: s.hart@bbk.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study triple-product-free sets, which are analogous to the widely studied concept of product-free sets. A nonempty subset S of a group G is triple-product-free if 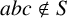$abc \notin S$ for all 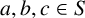$a, b, c \in S$. If S is triple-product-free and is not a proper subset of any other triple-product-free set, we say that S is locally maximal. We classify all groups containing a locally maximal triple-product-free set of size 1. We then derive necessary and sufficient conditions for a subset of a group to be locally maximal triple-product-free, and conclude with some observations and comparisons with the situation for standard product-free sets.

Keywords

sum-free setproduct-free setsolution-free settriple-product-free setfinite group

MSC classification

Primary: 20D60: Arithmetic and combinatorial problems
Secondary: 20F99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anabanti, C., ‘Groups containing locally maximal product-free sets of size 4’, Algebra Discrete Math. 31(2) (2021), 167–194.CrossRefGoogle Scholar
Anabanti, C. S. and Hart, S., ‘Groups containing small locally maximal product-free sets’, Internat. J. Comb. 2016 (2016), Article no. 8939182, 5 pages.Google Scholar
Giudici, M. and Hart, S., ‘Small maximal sum-free sets’, Electron. J. Combin. 16 (2009), 1–17.CrossRefGoogle Scholar
Khatirinejad, M. and Lisoněk, P., ‘Classification and constructions of complete caps in binary spaces’, Des. Codes Cryptogr. 39(1) (2006), 17–31.CrossRefGoogle Scholar
Schur, I., ‘Über die Kongruenz ${x}^m+{y}^m\cong {z}^m \text{ mod } p$ ’, Jahresber. Dtsch. Math.-Ver. 25 (1916), 114–117; reproduction, Gesammelte Abhandlungen, Vol. II (Springer-Verlag, Berlin–Heidelberg, 1973).Google Scholar