Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-17T22:33:21.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivalence of Besov spaces on p.c.f. self-similar sets

Part of: Classical measure theory Potential theory on metric spaces

Published online by Cambridge University Press:  26 May 2023

Shiping Cao Open the ORCID record for Shiping Cao [Opens in a new window]  and
Hua Qiu
Shiping Cao
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195, USA e-mail: spcao@uw.edu
Hua Qiu*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, China
*
e-mail: huaqiu@nju.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

On post-critically finite self-similar sets, whose walk dimensions of diffusions are in general larger than 2, we find a sharp region where two classes of Besov spaces, the heat Besov spaces 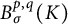$B^{p,q}_\sigma (K)$ and the Lipschitz–Besov spaces 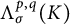$\Lambda ^{p,q}_\sigma (K)$, are identical. In particular, we provide concrete examples that 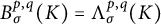$B^{p,q}_\sigma (K)=\Lambda ^{p,q}_\sigma (K)$ with 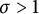$\sigma>1$. Our method is purely analytical, and does not involve heat kernel estimate.

Keywords

p.c.f. self-similar setsBesov spacesfractal analysisheat kernelsSobolev spaces

MSC classification

Primary: 28A80: Fractals
Secondary: 31E05: Potential theory on metric spaces
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 35
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of H.Q. was supported by the National Natural Science Foundation of China (Grant No. 12071213) and the Natural Science Foundation of Jiangsu Province in China (Grant No. BK20211142).

References

Alonso-Ruiz, P. and Baudoin, F., Gagliardo–Nirenberg, Trudinger–Moser and Morrey inequalities on Dirichlet spaces. J. Math. Anal. Appl. 497(2021), no. 2, 124899, 26 pp.CrossRefGoogle Scholar
Alonso-Ruiz, P., Baudoin, F., Chen, L., Rogers, L. G., Shanmugalingam, N., and Teplyaev, A., Besov class via heat semigroup on Dirichlet spaces I: Sobolev type inequalities . J. Funct. Anal. 278(2020), no. 11, 108459, 48 pp.CrossRefGoogle Scholar
Alonso-Ruiz, P., Baudoin, F., Chen, L., Rogers, L. G., Shanmugalingam, N., and Teplyaev, A., Besov class via heat semigroup on Dirichlet spaces II: BV functions and Gaussian heat kernel estimates . Calc. Var. Partial Differential Equations 59(2020), no. 3, Paper no. 103, 32 pp.CrossRefGoogle Scholar
Alonso-Ruiz, P., Baudoin, F., Chen, L., Rogers, L. G., Shanmugalingam, N., and Teplyaev, A., Besov class via heat semigroup on Dirichlet spaces II: BV functions and sub-Gaussian heat kernel estimates . Calc. Var. Partial Differential Equations 60(2021), no. 5, Paper no. 170, 38 pp.CrossRefGoogle Scholar
Barlow, M. T. and Bass, R. F., The construction of Brownian motion on the Sierpinski carpet . Ann. Inst. Henri Poincaré Probab. Stat. 25(1989), no. 3, 225–257.Google Scholar
Barlow, M. T., Bass, R. F., Kumagai, T., and Teplyaev, A., Uniqueness of Brownian motion on Sierpinski carpets . J. Eur. Math. Soc. (JEMS) 12(2010), no. 3, 655–701.Google Scholar
Barlow, M. T. and Perkins, E. A., Brownian motion on the Sierpiński gasket . Probab. Theory Related Fields 79(1988), no. 4, 543–623.CrossRefGoogle Scholar
Baudoin, F. and Chen, L., Sobolev spaces and Poincaré inequalities on the Vicsek fractal . Ann. Acad. Sci. Fenn. Math. 48(2023), no. 1, 3–26.CrossRefGoogle Scholar
Bergh, J. and Löfström, J., Interpolation spaces. An introduction, Grundlehren der Mathematischen Wissenschaften, 223, Springer, Berlin–New York, 1976.CrossRefGoogle Scholar
Cao, J. and Grigor’yan, A., Heat kernels and Besov spaces associated with second order divergence form elliptic operators . J. Fourier Anal. Appl. 26(2020), no. 1, Paper no. 3.CrossRefGoogle Scholar
Cao, J. and Grigor’yan, A., Heat kernels and Besov spaces on metric measure spaces . J. Anal. Math. 148(2022), no. 2, 637–680.CrossRefGoogle Scholar
Cao, S. and Qiu, H., Sobolev spaces on p.c.f. self-similar sets I: Critical orders and atomic decompositions . J. Funct. Anal. 282(2022), no. 4, Paper no. 109331.CrossRefGoogle Scholar
Cao, S. and Qiu, H., Sobolev spaces on p.c.f. self-similar sets II: Boundary behavior and interpolation theorems . Forum Math. 34(2022), no. 3, 749–779.CrossRefGoogle Scholar
Cao, S. and Qiu, H., Function spaces on p.c.f. self-similar sets III: Embedding and interpolation theorems, in preparation.Google Scholar
Gogatishvili, A., Koskela, P., and Shanmugalingam, N., Interpolation properties of Besov spaces defined on metric spaces . Math. Nachr. 283(2010), no. 2, 215–231.CrossRefGoogle Scholar
Goldstein, S., Random walks and diffusions on fractals . In: Percolation theory and ergodic theory of infinite particle systems (Minneapolis, MN, 1984–1985), The IMA Volumes in Mathematics and its Applications, 8, Springer, New York, 1987, pp. 121–129.Google Scholar
Grigor’yan, A., Heat kernels and function theory on metric measure spaces . In: Heat kernels and analysis on manifolds, graphs, and metric spaces (Paris, 2002), Contemporary Mathematics, 338, American Mathematical Society, Providence, RI, 2003, pp. 143–172.Google Scholar
Grigor'Yan, A., Hu, J., and Lau, K.-S., Heat kernels on metric measure spaces and an application to semilinear elliptic equations . Trans. Amer. Math. Soc. 355(2003), no. 5, 2065–2095.CrossRefGoogle Scholar
Grigor'yan, A. and Liu, L., Heat kernel and Lipschitz–Besov spaces . Forum Math. 27(2015), no. 6, 3567–3613.CrossRefGoogle Scholar
Haase, M., The functional calculus for sectorial operators, Operator Theory: Advances and Applications, 169, Birkäuser Verlag, Basel, 2006.CrossRefGoogle Scholar
Hambly, B. M. and Kumagai, T., Transition density estimates for diffusion processes on post critically finite self-similar fractals . Proc. Lond. Math. Soc. (3) 78(1999), no. 2, 431–458.CrossRefGoogle Scholar
Hinz, M., Koch, D., and Meinert, M., Sobolev spaces and calculus of variations on fractals. In: Analysis, probability and mathematical physics on fractals. Fractals Dyn. Math. Sci. Arts Theory Appl., World Scientific, Hackensack, NJ, 2020, pp. 419–450.CrossRefGoogle Scholar
Hu, J. and Zähle, M., Potential spaces on fractals . Stud. Math. 170(2005), no. 3, 259–281.CrossRefGoogle Scholar
Kigami, J., A harmonic calculus on the Sierpinski spaces . Jpn. J. Appl. Math. 6(1989), no. 2, 259–290.CrossRefGoogle Scholar
Kigami, J., A harmonic calculus on p.c.f. self-similar sets . Trans. Amer. Math. Soc. 335(1993), no. 2, 721–755.Google Scholar
Kigami, J., Analysis on fractals, Cambridge Tracts in Mathematics, 143, Cambridge University Press, Cambridge, 2001.CrossRefGoogle Scholar
Kigami, J., Geometry and analysis of metric spaces via weighted partitions, Lecture Notes in Mathematics, 2265, Springer, Cham, 2020, viii+162 pp.CrossRefGoogle Scholar
Kigami, J. and Lapidus, M. L., Weyl’s problem for the spectral distribution of Laplacians on p.c.f. self-similar fractals . Comm. Math. Phys. 158(1993), no. 1, 93–125.CrossRefGoogle Scholar
Kumagai, T. and Sturm, K. T., Construction of diffusion processes on fractals, d-sets, and general metric measure spaces . J. Math. Kyoto Univ. 45(2005), no. 2, 307–327.Google Scholar
Kusuoka, S. and Zhou, X. Y., Dirichlet forms on fractals: Poincaré constant and resistance . Probab. Theory Related Fields 93(1992), no. 2, 169–196.CrossRefGoogle Scholar
Lindstrøm, T., Brownian motion on nested fractals . Mem. Amer. Math. Soc. 83(1990), no. 420, iv+128 pp.Google Scholar
Pietruska-Pałuba, K., On function spaces related to fractional diffusions on d-sets . Stoch. Rep. 70(2000), 153–164.CrossRefGoogle Scholar
Rogers, L. G., Strichartz, R. S., and Teplyaev, A., Smooth bumps, a Borel theorem and partitions of smooth functions on p.c.f. fractals . Trans. Amer. Math. Soc. 361(2009), 1765–1790.CrossRefGoogle Scholar
Strichartz, R. S., Function spaces on fractals . J. Funct. Anal. 198(2003), no. 1, 43–83.CrossRefGoogle Scholar
Strichartz, R. S., Analysis on products of fractals . Trans. Amer. Math. Soc. 357(2005), no. 2, 571–615.CrossRefGoogle Scholar
Strichartz, R. S., Differential equations on fractals: A tutorial, Princeton University Press, Princeton, NJ, 2006.CrossRefGoogle Scholar
Teplyaev, A., Gradients on fractals . J. Funct. Anal. 174(2000), no. 1, 128–154.CrossRefGoogle Scholar
Triebel, H., Interpolation theory, function spaces, differential operators. Second ed., Johann Ambrosius Barth, Heidelberg, 1995.Google Scholar