No CrossRef data available.
Article contents
On webs in quantum type C
Published online by Cambridge University Press: 26 February 2021
Abstract
We study webs in quantum type C, focusing on the rank three case. We define a linear pivotal category 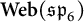 $\textbf {Web}(\mathfrak {sp}_{6})$
diagrammatically by generators and relations, and conjecture that it is equivalent to the category
$\textbf {Web}(\mathfrak {sp}_{6})$
diagrammatically by generators and relations, and conjecture that it is equivalent to the category
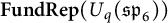 $\textbf {FundRep}(U_q(\mathfrak {sp}_{6}))$
of quantum
$\textbf {FundRep}(U_q(\mathfrak {sp}_{6}))$
of quantum
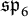 $\mathfrak {sp}_{6}$
representations generated by the fundamental representations, for generic values of the parameter q. We prove a number of results in support of this conjecture, most notably that there is a full, essentially surjective functor
$\mathfrak {sp}_{6}$
representations generated by the fundamental representations, for generic values of the parameter q. We prove a number of results in support of this conjecture, most notably that there is a full, essentially surjective functor
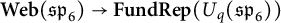 $\textbf {Web}(\mathfrak {sp}_{6}) \rightarrow \textbf {FundRep}(U_q(\mathfrak {sp}_{6}))$
, that all
$\textbf {Web}(\mathfrak {sp}_{6}) \rightarrow \textbf {FundRep}(U_q(\mathfrak {sp}_{6}))$
, that all
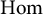 $\textrm {Hom}$
-spaces in
$\textrm {Hom}$
-spaces in
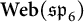 $\textbf {Web}(\mathfrak {sp}_{6})$
are finite-dimensional, and that the endomorphism algebra of the monoidal unit in
$\textbf {Web}(\mathfrak {sp}_{6})$
are finite-dimensional, and that the endomorphism algebra of the monoidal unit in
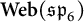 $\textbf {Web}(\mathfrak {sp}_{6})$
is one-dimensional. The latter corresponds to the statement that all closed webs can be evaluated to scalars using local relations; as such, we obtain a new approach to the quantum
$\textbf {Web}(\mathfrak {sp}_{6})$
is one-dimensional. The latter corresponds to the statement that all closed webs can be evaluated to scalars using local relations; as such, we obtain a new approach to the quantum
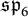 $\mathfrak {sp}_{6}$
link invariants, akin to the Kauffman bracket description of the Jones polynomial.
$\mathfrak {sp}_{6}$
link invariants, akin to the Kauffman bracket description of the Jones polynomial.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
This work was supported in part by Simons Collaboration Grant 523992: Research on knot invariants, representation theory, and categorification.





