Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-06-01T10:52:10.082Z Has data issue: false hasContentIssue false
  • English
  • Français

Prime Producing Quadratic Polynomials and Class-Numbers of Real Quadratic Fields

Published online by Cambridge University Press:  20 November 2018

Stéphane Louboutin
Stéphane Louboutin*
Affiliation:
University of Caen, Caen, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Frobenius-Rabinowitsch's theorem provides us with a necessary and sufficient condition for the class-number of a complex quadratic field with negative discriminant D to be one in terms of the primality of the values taken by the quadratic polynomial 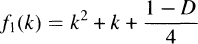with discriminant Don consecutive integers (See [1], [7]). M. D. Hendy extended Frobenius-Rabinowitsch's result to a necessary and sufficient condition for the class-number of a complex quadratic field with discriminant D to be two in terms of the primality of the values taken by the quadratic polynomials 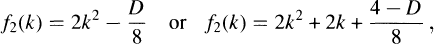and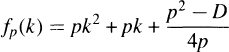 with discriminant D (see [2], [7]).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 2 , 01 April 1990 , pp. 315 - 341
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Chowla, S., On Euler's polynomial, J. of Nb. Th. 13 (1981), 443–445.Google Scholar
2. Hendy, M.D., Prime quadratics associated with complex quadratic fields of class-number two, P.A.M.S. 43 (1974), 253–266.Google Scholar
3. Kutsuna, M., On a criterion for the class number of a quadratic number field to be one, Nagoya Math. J. 79 (1980), 123-129.Google Scholar
4. Louboutin, S., Arithmétique des corps quadratiques réels et fractions continues, Thèse de Doctorat, Université Paris 7 (1987).Google Scholar
5. Louboutin, S., Continuedfractions and real quadratic fields, J. of Nb. Th. 30 (1988), 167–176.Google Scholar
6. Louboutin, S., Groupe des classes d'idéaux triviaux, To appear, Acta Arithmetica 54. Google Scholar
7. Louboutin, S., Prime producing quadratic polynomials and class-numbers of complex quadratic fields, To appear.Google Scholar
8. Mollin, R.A., Class number one criteria for real quadratic fields, Proc. Japan Acad. 63, Ser. A (1987).Google Scholar
9. Mollin, R.A. and Williams, H.C., On prime valued polynomials and class number of real quadratic fields, Nagoya Math. J. 12 (1988), 143–151.Google Scholar
10. Mollin, R.A. and Williams, H.C., Prime producing quadratic polynomials and real quadratic fields of class-number one, Théorie des nombres/ Number theory “Comptes Rendus de la Conférence Internationale de Théorie des Nombres tenue à l'Université Laval en 1987/ Proceedings of the International Number Theory Conference held at Université Laval in 1987 (W. de Gruyter, Berlin, New York, 1989).Google Scholar
11. Mollin, A. and Williams, H.C., Solution of the class-number one problem for real quadratic fields of Richaud-Degert type, Proc. of the first Conf. of the Canadian Number Theory Assoc, held at the Banff Center, Banff, Alberta, April 17-27 1988 (W. de Gruyter, Berlin, New York, 1989).Google Scholar
12. Mollin, A. and Williams, H.C., Class-number one for real quadratic fields, continued fractions and reduced ideals, Proc. of the NATO ASI on Nb. Th. and Applications, Banff 1988 (Kluwer Academic Publishers, Netherlands, 1989).Google Scholar
13. Sasaki, R., A characterisation of certain real quadratic fields, Proc. Japan Acad. 62, Ser. A (1986), 97–100.Google Scholar
14. Sasaki, R., Generalized Ono invariants and Rabinovitch's theorem for real quadratic fields, Nagoya Math. J. 709 (1988), 117-124.Google Scholar
15. Yokoi, H., Class-number one problem for certain kind of real quadratic fields, Proc. Int. Conf. on Class Numbers and Fundamental Units, Katata, Japan (1986).Google Scholar

An addendum has been issued for this article:

Addendum