No CrossRef data available.
Article contents
Exceptional Covers of Surfaces
Published online by Cambridge University Press: 20 November 2018
Abstract
Consider a finite morphism 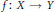 $f\,:\,X\,\to \,Y$ of smooth, projective varieties over a finite field
$f\,:\,X\,\to \,Y$ of smooth, projective varieties over a finite field 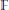 $\mathbb{F}$. Suppose
$\mathbb{F}$. Suppose 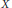 $X$ is the vanishing locus in
$X$ is the vanishing locus in 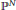 ${{\mathbb{P}}^{N}}$ of
${{\mathbb{P}}^{N}}$ of  $r$ forms of degree at most
$r$ forms of degree at most  $d$. We show that there is a constant
$d$. We show that there is a constant  $C$ depending only on
$C$ depending only on 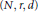 $(N,\,r,\,d)$ and
$(N,\,r,\,d)$ and 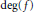 $\deg (f)$ such that if
$\deg (f)$ such that if 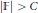 $\left| \mathbb{F} \right|\,>\,C$, then
$\left| \mathbb{F} \right|\,>\,C$, then 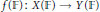 $f\,(\mathbb{F})\,:\,X(\mathbb{F})\,\to Y(\mathbb{F})$ is injective if and only if it is surjective.
$f\,(\mathbb{F})\,:\,X(\mathbb{F})\,\to Y(\mathbb{F})$ is injective if and only if it is surjective.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010




