Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-05-28T14:46:56.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear Beltrami equation: lower estimates of Schwarz lemma’s type

Part of: Geometric function theory Functions of several variables Classical measure theory General properties

Published online by Cambridge University Press:  29 November 2023

Igor Petkov Open the ORCID record for Igor Petkov [Opens in a new window] ,
Ruslan Salimov Open the ORCID record for Ruslan Salimov [Opens in a new window]  and
Mariia Stefanchuk Open the ORCID record for Mariia Stefanchuk [Opens in a new window]
Igor Petkov
Affiliation:
Admiral Makarov National University of Shipbuilding, 9 Heroes of Ukraine Avenue, Mykolaiv 54007, Ukraine e-mail: igorpetkov83@gmail.com
Ruslan Salimov*
Affiliation:
Institute of Mathematics of NAS of Ukraine, 3 Tereschenkivska Street, Kyiv-4 01024, Ukraine e-mail: stefanmv43@gmail.com
Mariia Stefanchuk
Affiliation:
Institute of Mathematics of NAS of Ukraine, 3 Tereschenkivska Street, Kyiv-4 01024, Ukraine e-mail: stefanmv43@gmail.com
*
e-mail: ruslan.salimov1@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a nonlinear Beltrami equation 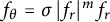$f_\theta =\sigma \,|f_r|^m f_r$ in polar coordinates 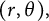$(r,\theta ),$ which becomes the classical Cauchy–Riemann system under 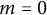$m=0$ and 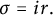$\sigma =ir.$ Using the isoperimetric technique, various lower estimates for 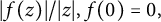$|f(z)|/|z|, f(0)=0,$ as 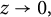$z\to 0,$ are derived under appropriate integral conditions on complex/directional dilatations. The sharpness of the above bounds is illustrated by several examples.

Keywords

Beltrami equationnonlinear Beltrami equationnonlinear Cauchy–Riemann systemasymptotic behaviorSchwarz lemma

MSC classification

Primary: 28A75: Length, area, volume, other geometric measure theory 30A10: Inequalities in the complex domain
Secondary: 26B15: Integration 30C80: Maximum principle; Schwarz's lemma, Lindelöf principle, analogues and generalizations; subordination
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamowicz, T., On $p$ -harmonic mappings in the plane . Nonlinear Anal. 71(2009), nos. 1–2, 502–511.CrossRefGoogle Scholar
Andreian Cazacu, C., Influence of the orientation of the characteristic ellipses on the properties of the quasiconformal mappings . In: Proceedings of the Romanian-Finnish seminar on Teichmüller spaces and quasiconformal mappings. Braşov 1969, Publishing House of the Academy of the Socialist Republic of Romania, Bucharest, 1971, pp. 65–85.Google Scholar
Aronsson, G., On certain $p$ -harmonic functions in the plane . Manuscripta Math. 61(1988), no. 1, 79–101.CrossRefGoogle Scholar
Astala, K., Clop, A., Faraco, D., Jääskeläinen, J., and Koski, A., Nonlinear Beltrami operators, Schauder estimates and bounds for the Jacobian . Ann. Inst. H. Poincaré Anal. Non Linéaire 34(2017), no. 6, 1543–1559.Google Scholar
Astala, K., Iwaniec, T., and Martin, G., Elliptic partial differential equations and quasiconformal mappings in the plane, Princeton Mathematical Series, 48, Princeton University Press, Princeton, NJ, 2009.Google Scholar
Bojarski, B., Gutlyanskiĭ, V., Martio, O., and Ryazanov, V., Infinitesimal geometry of quasiconformal and bi-Lipschitz mappings in the plane. EMS Tracts in Mathematics, 19, European Mathematical Society, Zürich, 2013.CrossRefGoogle Scholar
Bojarski, B. and Iwaniec, T., p-harmonic equation and quasiregular mappings . In: Partial differential equations (Warsaw, 1984), Banach Center Publications, 19, PWN, Warsaw, 1987, pp. 25–38.Google Scholar
Carozza, M., Giannetti, F., di Napoli, A. P., Sbordone, C., and Schiattarella, R., Bi-Sobolev mappings and ${K}_p$ -distortions in the plane . J. Math. Anal. Appl. 457(2018), no. 2, 1232–1246.CrossRefGoogle Scholar
Golberg, A., Directional dilatations in space . Complex Var. Elliptic Equ. 55(2010), nos. 1–3, 13–29.CrossRefGoogle Scholar
Golberg, A., Extremal bounds of Teichmüller–Wittich–Belinskiĭ type for planar quasiregular mappings . In: New trends in approximation theory, Fields Institute Communications, 81, Springer, New York, 2018, pp. 173–199.CrossRefGoogle Scholar
Golberg, A. and Salimov, R., Nonlinear Beltrami equation . Complex Var. Elliptic Equ. 65(2020), no. 1, 6–21.CrossRefGoogle Scholar
Golberg, A., Salimov, R., and Stefanchuk, M., Asymptotic dilation of regular homeomorphisms . Compl. Anal. Oper. Theory 13(2019), no. 6, 2813–2827.CrossRefGoogle Scholar
Guo, C.-Y. and Kar, M., Quantitative uniqueness estimates for $p$ -Laplace type equations in the plane . Nonlinear Anal. 143(2016), 19–44.CrossRefGoogle Scholar
Gutlyanskiĭ, V., Ryazanov, V., Srebro, U., and Yakubov, E., On recent advances in the Beltrami equations . Ukr. Mat. Visn. 7(2010), no. 4, 467–515; reprinted in J. Math. Sci. (N.Y.) 175(2011), no. 4, 413–449.Google Scholar
Gutlyanskiĭ, V., Ryazanov, V., Srebro, U., and Yakubov, E., The Beltrami equation. A geometric approach. Developments in Mathematics, 26, Springer, New York, 2012.CrossRefGoogle Scholar
Ikoma, K., On the distortion and correspondence under quasiconformal mappings in space . Nagoya Math. J. 25(1965), 175–203.CrossRefGoogle Scholar
Kruschkal, S. L. and Kühnau, R., Quasikonforme Abbildungen-neue Methoden und Anwendungen. German . In: Quasiconformal mappings – new methods and applications with English, French and Russian summaries, Teubner-Texte zur Mathematik (Teubner Texts in Mathematics), 54, BSB B. G. Teubner Verlagsgesellschaft, Leipzig, 1983.Google Scholar
Kühnau, R., Minimal surfaces and quasiconformal mappings in the mean . Zbir. Prats. Inst. Mat. NANU 7(2010), no. 2, 104–131.Google Scholar
Lavrent’ev, M. A., A general problem of the theory of quasi-conformal representation of plane regions . Mat. Sbornik N.S. 21(1947), no. 63, 285–320 (in Russian).Google Scholar
Lavrent’ev, M. A., The variational method in boundary-value problems for systems of equations of elliptic type . Izdat. Akad. Nauk SSSR, Sibirskoe otdelenie, Moskva (1962), 136 (Russian).Google Scholar
Lavrent’ev, M. A. and Šabat, B. V., Geometrical properties of solutions of non-linear systems of partial differential equations . Dokl. Akad. Nauk SSSR (N.S.) 112(1957), 810–811 (in Russian).Google Scholar
Lehto, O. and Virtanen, K. I., Quasiconformal mappings in the plane. 2nd ed., Die Grundlehren der mathematischen Wissenschaften, 126, Springer, New York–Heidelberg, 1973, translated from the German by K. W. Lucas.CrossRefGoogle Scholar
Martio, O., Ryazanov, V., Srebro, U., and Yakubov, E., Moduli in modern mapping theory. Springer Monographs in Mathematics, Springer, New York, 2009.Google Scholar
Martio, O. and Ziemer, W. P., Lusin’s condition (N) and mappings with nonnegative Jacobians . Michigan Math. J. 39(1992), no. 3, 495–508.CrossRefGoogle Scholar
Romanov, A. S., Capacity relations in a planar quadrilateral . Sibirsk. Mat. Zh. 49 (2008), no. 4, 886–897 (in Russian), translation in Sib. Math. J. 49(2008), no. 4, 709–717.Google Scholar
Ryazanov, V., Srebro, U., and Yakubov, E., On ring solutions of Beltrami equations . J. Anal. Math. 96(2005), 117–150.CrossRefGoogle Scholar
Šabat, B. V., Geometric interpretation of the concept of ellipticity . Uspehi Mat. Nauk. 12(1957), no. 6(78), 181–188 (in Russian).Google Scholar
Šabat, B. V., On the notion of derivative system according to M. A. Lavrent’ev . Dokl. Akad. Nauk SSSR 136(1961), 1298–1301 (in Russian), translated as Soviet Math. Dokl. 2(1961), 202–205.Google Scholar
Saks, S., Theory of the integral, Dover, New York, 1964.Google Scholar
Salimov, R. and Stefanchuk, M., Finite Lipschitzness of regular solutions to nonlinear Beltrami equation . Complex Var. Elliptic Equ., published online 12.01.2023. https://doi.org/10.1080/17476933.2023.2166498 CrossRefGoogle Scholar
Salimov, R. R. and Stefanchuk, M. V., On the local properties of solutions of the nonlinear Beltrami equation . J. Math. Sci. 248(2020), 203–216.CrossRefGoogle Scholar
Salimov, R. R. and Stefanchuk, M. V., Logarithmic asymptotics of the nonlinear Cauchy–Riemann–Beltrami equation . Ukr. Math. J. 73(2021), 463–478.CrossRefGoogle Scholar
Salimov, R. R. and Stefanchuk, M. V., Nonlinear Beltrami equation and asymptotics of its solution . J. Math. Sci. 264(2022), no. 4, 441–454.CrossRefGoogle Scholar
Sevost’yanov, E. A., On quasilinear Beltrami-type equations with degeneration . Mat. Zametki 90(2011), no. 3, 445–453 (in Russian); translation in Math. Notes 90(2011), no. 3–4, 431–438.Google Scholar
Srebro, U. and Yakubov, E., Beltrami equation . In: Handbook of complex analysis: geometric function theory. Vol. 2, Elsevier Science B. V., Amsterdam, 2005, pp. 555–597.CrossRefGoogle Scholar