Hostname: page-component-cb9f654ff-nr592 Total loading time: 0 Render date: 2025-08-28T06:14:44.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Spanning trees in graphs without large bipartite holes

Part of: Graph theory

Published online by Cambridge University Press:  14 November 2023

Jie Han ,
Jie Hu ,
Lidan Ping ,
Guanghui Wang ,
Yi Wang  and
Donglei Yang
Jie Han
Affiliation:
School of Mathematics and Statistics and Center for Applied Mathematics, Beijing Institute of Technology, Beijing, China
Jie Hu
Affiliation:
Center for Combinatorics and LPMC, Nankai University, Tianjin, China
Lidan Ping
Affiliation:
School of Mathematics, Shandong University, Jinan, China
Guanghui Wang
Affiliation:
School of Mathematics, Shandong University, Jinan, China
Yi Wang
Affiliation:
Data Science Institute, Shandong University, Jinan, China
Donglei Yang*
Affiliation:
School of Mathematics, Shandong University, Jinan, China
*
Corresponding author: Donglei Yang; Email: dlyang@sdu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

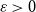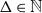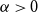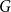We show that for any $\varepsilon \gt 0$ and $\Delta \in \mathbb{N}$, there exists $\alpha \gt 0$ such that for sufficiently large $n$, every $n$-vertex graph $G$ satisfying that $\delta (G)\geq \varepsilon n$ and 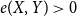$e(X, Y)\gt 0$ for every pair of disjoint vertex sets 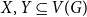$X, Y\subseteq V(G)$ of size 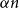$\alpha n$ contains all spanning trees with maximum degree at most $\Delta$. This strengthens a result of Böttcher, Han, Kohayakawa, Montgomery, Parczyk, and Person.

Keywords

Bipartite holesspanning treesabsorbing method

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C05: Trees

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 33 , Issue 3 , May 2024 , pp. 270 - 285
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Jie Hu: Supported by Natural Science Foundation of China (12131013, 12161141006). Guanghui Wang: Research supported by Natural Science Foundation of China (12231018) and Young Taishan Scholars probgram of Shandong Province (201909001). Donglei Yang: Supported by the China Post-doctoral Science Foundation (2021T140413), Natural Science Foundation of China (12101365) and Natural ScienceFoundation of Shandong Province (ZR2021QA029).

References

Balogh, J., Molla, T. and Sharifzadeh, M. (2016) Triangle factors of graphs without large independent sets and of weighted graphs. Random Struct. Algorithms 49(4) 669–693.10.1002/rsa.20670CrossRefGoogle Scholar
Bohman, T., Frieze, A. and Martin, R. (2003) How many random edges make a dense graph hamiltonian? Random Struct. Algorithms 22(1) 33–42.10.1002/rsa.10070CrossRefGoogle Scholar
Böttcher, J., Han, J., Kohayakawa, Y., Montgomery, R., Parczyk, O. and Person, Y. (2019) Universality for bounded degree spanning trees in randomly perturbed graphs. Random Struct. Algorithms 55(4) 854–864.10.1002/rsa.20850CrossRefGoogle Scholar
Böttcher, J., Schacht, M. and Taraz, A. (2009) Proof of the bandwidth conjecture of Bollobás and Komlós. Math. Ann. 343(1) 175–20531.10.1007/s00208-008-0268-6CrossRefGoogle Scholar
Chang, F., Han, J., Kim, J., Wang, G. and Yang, D. (2023) Embedding clique-factors in graphs with low $\ell$ -independence number. J. Comb. Theory Ser. B 161 301–330.10.1016/j.jctb.2023.02.008CrossRefGoogle Scholar
Corrádi, K. and Hajnal, A. (1963) On the maximal number of independent circuits in graph. Acta Math. Acad. Sci. Hung. 14(3-4) 423–439.10.1007/BF01895727CrossRefGoogle Scholar
Dirac, G. A. (1952) Some theorems on abstract graphs. Proc. Lond. Math. Soc. 3(1) 69–81.10.1112/plms/s3-2.1.69CrossRefGoogle Scholar
Draganić, N., Correia, D. M. and Sudakov, B. (2023) A generalization of bondy’s pancyclicity theorem. arXiv preprint arXiv: 2302.12752.10.5817/CZ.MUNI.EUROCOMB23-051CrossRefGoogle Scholar
Ergemlidze, B. and Molla, T. (2022) Transversal ${C}_k$ -factors in subgraphs of the balanced blow-up of ${C}_k$ . Comb. Probab. Comput. 31(6) 1031–1047.CrossRefGoogle Scholar
Fischer, E. (1999) Variants of the Hajnal–Szemerédi theorem. J. Graph Theory 31 275–282.10.1002/(SICI)1097-0118(199908)31:4<275::AID-JGT2>3.0.CO;2-F3.0.CO;2-F>CrossRefGoogle Scholar
Friedman, J. (2008) A proof of Alon’s second eigenvalue conjecture. Mem. Am. Math. Soc. 195(910) viii+100.Google Scholar
Friedman, J. and Pippenger, N. (1987) Expanding graphs contain all small trees. Combinatorica 7(1) 71–76.CrossRefGoogle Scholar
Han, J. (2017) Decision problem for perfect matchings in dense $k$ -uniform hypergraphs. Trans. Am. Math. Soc. 369(7) 5197–5218.10.1090/tran/6999CrossRefGoogle Scholar
Han, J., Hu, P., Wang, G. and Yang, D. (2023) Clique-factors in graphs with sublinear $\ell$ -independence number. Comb. Prob. Comput. 32(4) 665–681.Google Scholar
Han, J., Morris, P., Wang, G. and Yang, D. (2023) A Ramsey–Turán theory for tilings in graphs. Random Struct. Algorithms, 1–31. doi:10.1002/rsa.21182.Google Scholar
Haxell, P. E. (2001) Tree embeddings. J. Graph Theory 36(3) 121–130.10.1002/1097-0118(200103)36:3<121::AID-JGT1000>3.0.CO;2-U3.0.CO;2-U>CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization, New York 10.1002/9781118032718CrossRefGoogle Scholar
Johannsen, D., Krivelevich, M. and Samotij, W. (2013) Expanders are universal for the class of all spanning trees. Comb. Prob. Comput. 22(2) 253–281.10.1017/S0963548312000533CrossRefGoogle Scholar
Johansson, R. (2000) Triangle-factors in a balanced blown-up triangle. Discrete Math. 211(1-3) 249–254.10.1016/S0012-365X(99)00324-6CrossRefGoogle Scholar
Keevash, P. and Mycroft, R. (2015) A multipartite Hajnal–Szemerédi theorem. J. Comb. Theory Ser. B 114 187–236.10.1016/j.jctb.2015.04.003CrossRefGoogle Scholar
Kim, J., Kim, Y. and Liu, H. (2020) Tree decompositions of graphs without large bipartite holes. Random Struct. Algorithms 57(1) 150–168.10.1002/rsa.20913CrossRefGoogle Scholar
Knierim, C. and Su, P. (2021) ${K}_r$ -factors in graphs with low independence number. J. Comb. Theory Ser. B 148 60–83.CrossRefGoogle Scholar
Komlós, J. (1999) The blow-up lemma. Comb. Prob. Comput. 8(1-2) 161–176.CrossRefGoogle Scholar
Komlós, J., Sárközy, G. N. and Szemerédi, E. (1995) Proof of a packing conjecture of Bollobás. Comb. Prob. Comput. 4(3) 241–255.CrossRefGoogle Scholar
Komlós, J., Sárközy, G. N. and Szemerédi, E. (2001) Spanning trees in dense graphs. Comb. Prob. Comput. 10(5) 397–416.CrossRefGoogle Scholar
Komlós, J. and Simonovits, M. (1996) Szemerédi’s regularity lemma and its applications in graph theory. Combinatorica 2 295–352.Google Scholar
Krivelevich, M. (2010) Embedding spanning trees in random graphs. SIAM J. Discrete Math. 24(4) 1495–1500.CrossRefGoogle Scholar
Krivelevich, M., Kwan, M. and Sudakov, B. (2017) Bounded-degree spanning trees in randomly perturbed graphs. SIAM J. Discrete Math. 31(1) 155–171.10.1137/15M1032910CrossRefGoogle Scholar
Lo, A. and Markström, K. (2013) A multipartite version of the Hajnal–Szemerédi theorem for graphs and hypergraphs. Comb. Prob. Comput. 22(1) 97–111.CrossRefGoogle Scholar
Lovász, L. and Plummer, M. D. (2009) Matching Theory. American Mathematical Society Press.Google Scholar
Magyar, C. and Martin, R. (2002) Tripartite version of the Corrádi–Hajnal theorem. Discrete Math. 254(1-3) 289–308.10.1016/S0012-365X(01)00373-9CrossRefGoogle Scholar
Martin, R. and Szemerédi, E. (2008) Quadripartite version of the Hajnal–Szemerédi theorem. Discrete Math. 308(19) 4337–4360.CrossRefGoogle Scholar
Mcdiarmid, C. and Yolov, N. (2017) Hamilton cycles, minimum degree and bipartite holes. J. Graph Theory 86(3) 277–285.CrossRefGoogle Scholar
Montgomery, R. (2019) Spanning trees in random graphs. Adv. Math. 356 106793.10.1016/j.aim.2019.106793CrossRefGoogle Scholar
Nenadov, R. and Pehova, Y. (2020) On a Ramsey–Turán variant of the Hajnal–Szemerédi theorem. SIAM J. Discrete Math. 34(2) 1001–1010.CrossRefGoogle Scholar