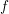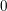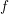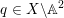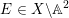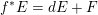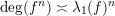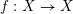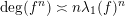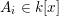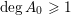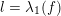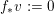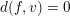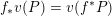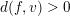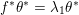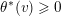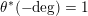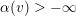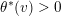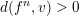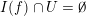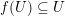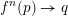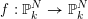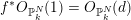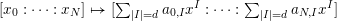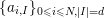1 Introduction
Denote by
![]() $k$
an algebraically closed field of characteristic
$k$
an algebraically closed field of characteristic
![]() $0$
.
$0$
.
The aim of this paper is to prove the following result.
Theorem 1.1. Let
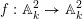 $f:\mathbb{A}_{k}^{2}\rightarrow \mathbb{A}_{k}^{2}$
be a dominant polynomial endomorphism. If there are no nonconstant rational functions
$f:\mathbb{A}_{k}^{2}\rightarrow \mathbb{A}_{k}^{2}$
be a dominant polynomial endomorphism. If there are no nonconstant rational functions
![]() $g$
satisfying
$g$
satisfying
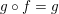 $g\circ f=g$
, then there exists a point
$g\circ f=g$
, then there exists a point
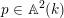 $p\in \mathbb{A}^{2}(k)$
such that the orbit
$p\in \mathbb{A}^{2}(k)$
such that the orbit
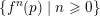 $\{f^{n}(p)\mid n\geqslant 0\}$
of
$\{f^{n}(p)\mid n\geqslant 0\}$
of
![]() $p$
is Zariski dense in
$p$
is Zariski dense in
![]() $\mathbb{A}_{k}^{2}$
.
$\mathbb{A}_{k}^{2}$
.
We cannot ask
![]() $g$
in Theorem 1.1 to be a polynomial. Indeed, let
$g$
in Theorem 1.1 to be a polynomial. Indeed, let
![]() $P(x,y)$
be a polynomial which is neither zero nor a root of unity. Let
$P(x,y)$
be a polynomial which is neither zero nor a root of unity. Let
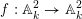 $f:\mathbb{A}_{k}^{2}\rightarrow \mathbb{A}_{k}^{2}$
be the endomorphism defined by
$f:\mathbb{A}_{k}^{2}\rightarrow \mathbb{A}_{k}^{2}$
be the endomorphism defined by
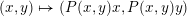 $(x,y)\mapsto (P(x,y)x,P(x,y)y)$
. It is easy to see that
$(x,y)\mapsto (P(x,y)x,P(x,y)y)$
. It is easy to see that
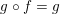 $g\circ f=g$
if
$g\circ f=g$
if
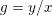 $g=y/x$
, but there does not exist any polynomial
$g=y/x$
, but there does not exist any polynomial
![]() $h$
satisfying
$h$
satisfying
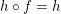 $h\circ f=h$
.
$h\circ f=h$
.
The following conjecture was proposed by Medvedev and Scanlon [Reference Medvedev and ScanlonMS09, Conjecture 5.10] and also by Amerik et al. [Reference Amerik, Bogomolov and RovinskyAB11].
Conjecture 1.2. Let
![]() $X$
be a quasiprojective variety over
$X$
be a quasiprojective variety over
![]() $k$
and
$k$
and
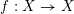 $f:X\rightarrow X$
be a dominant endomorphism for which there exists no nonconstant rational function
$f:X\rightarrow X$
be a dominant endomorphism for which there exists no nonconstant rational function
![]() $g$
satisfying
$g$
satisfying
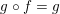 $g\circ f=g$
. Then there exists a point
$g\circ f=g$
. Then there exists a point
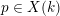 $p\in X(k)$
whose orbit is Zariski dense in
$p\in X(k)$
whose orbit is Zariski dense in
![]() $X$
.
$X$
.
Conjecture 1.2 strengthens the following conjecture of Zhang [Reference ZhangZha06].
Conjecture 1.3. Let
![]() $X$
be a projective variety and
$X$
be a projective variety and
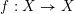 $f:X\rightarrow X$
be an endomorphism defined over
$f:X\rightarrow X$
be an endomorphism defined over
![]() $k$
. If there exists an ample line bundle
$k$
. If there exists an ample line bundle
![]() $L$
on
$L$
on
![]() $X$
satisfying
$X$
satisfying
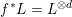 $f^{\ast }L=L^{\otimes d}$
for some integer
$f^{\ast }L=L^{\otimes d}$
for some integer
![]() $d>1$
, then there exists a point
$d>1$
, then there exists a point
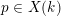 $p\in X(k)$
whose orbit
$p\in X(k)$
whose orbit
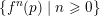 $\{f^{n}(p)\mid n\geqslant 0\}$
is Zariski dense in
$\{f^{n}(p)\mid n\geqslant 0\}$
is Zariski dense in
![]() $X(k)$
.
$X(k)$
.
Theorem 1.1 settles Conjecture 1.2 for polynomial endomorphisms of
![]() $\mathbb{A}_{k}^{2}$
.
$\mathbb{A}_{k}^{2}$
.
When
![]() $k$
is uncountable, Conjecture 1.2 was proved by Amerik and Campana [Reference Amerik and CampanaAC08]. In [Reference FakhruddinFak14], Fakhruddin proved Conjecture 1.2 for
$k$
is uncountable, Conjecture 1.2 was proved by Amerik and Campana [Reference Amerik and CampanaAC08]. In [Reference FakhruddinFak14], Fakhruddin proved Conjecture 1.2 for
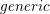 $generic$
Footnote
1
endomorphisms on projective spaces over arbitrary algebraically closed fields
$generic$
Footnote
1
endomorphisms on projective spaces over arbitrary algebraically closed fields
![]() $k$
of characteristic
$k$
of characteristic
![]() $0$
. In [Reference XieXie15b], the author proved Conjecture 1.2 for birational surface endomorphisms with dynamical degree greater than
$0$
. In [Reference XieXie15b], the author proved Conjecture 1.2 for birational surface endomorphisms with dynamical degree greater than
![]() $1$
. Recently, in [Reference Medvedev and ScanlonMS14], Medvedev and Scanlon proved Conjecture 1.2 when
$1$
. Recently, in [Reference Medvedev and ScanlonMS14], Medvedev and Scanlon proved Conjecture 1.2 when
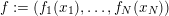 $f:=(f_{1}(x_{1}),\ldots ,f_{N}(x_{N}))$
is an endomorphism of
$f:=(f_{1}(x_{1}),\ldots ,f_{N}(x_{N}))$
is an endomorphism of
![]() $\mathbb{A}_{k}^{N}$
, where the
$\mathbb{A}_{k}^{N}$
, where the
![]() $f_{i}$
are one-variable polynomials defined over
$f_{i}$
are one-variable polynomials defined over
![]() $k$
.
$k$
.
We mention that in [Reference AmerikAme11], Amerik proved that there exists a nonpreperiodic algebraic point when
![]() $f$
is of infinite order. In [Reference Bell, Ghioca and TuckerBGT15], Bell et al. proved that if
$f$
is of infinite order. In [Reference Bell, Ghioca and TuckerBGT15], Bell et al. proved that if
![]() $f$
is an automorphism, then there exists a subvariety of codimension
$f$
is an automorphism, then there exists a subvariety of codimension
![]() $2$
whose orbit under
$2$
whose orbit under
![]() $f$
is Zariski dense.
$f$
is Zariski dense.
We note that Conjecture 1.2 is not true in the case when
![]() $k$
is the algebraic closure of a finite field, since in this case all orbits of
$k$
is the algebraic closure of a finite field, since in this case all orbits of
![]() $k$
-points are finite.
$k$
-points are finite.
Our proof of Theorem 1.1 is based on the valuative techniques developed in [Reference Favre and JonssonFJ04, Reference Favre and JonssonFJ07, Reference Favre and JonssonFJ11, Reference XieXie15a]. Here is an outline of the proof.
For simplicity, suppose that
![]() $f$
is a dominant polynomial map
$f$
is a dominant polynomial map
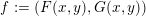 $f:=(F(x,y),G(x,y))$
defined over
$f:=(F(x,y),G(x,y))$
defined over
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
When
![]() $f$
is birational, our Theorem 1.1 is essentially proved in [Reference XieXie15b]. So, we may suppose that
$f$
is birational, our Theorem 1.1 is essentially proved in [Reference XieXie15b]. So, we may suppose that
![]() $f$
is not birational.
$f$
is not birational.
By [Reference Favre and JonssonFJ11], there exists a projective compactification
![]() $X$
of
$X$
of
![]() $\mathbb{A}^{2}$
for which the induced map by
$\mathbb{A}^{2}$
for which the induced map by
![]() $f$
at infinity is algebraically stable, i.e. it does not contract any curve to a point of indeterminacy. Moreover, we can construct an ‘attracting locus’ at infinity, in the sense that:
$f$
at infinity is algebraically stable, i.e. it does not contract any curve to a point of indeterminacy. Moreover, we can construct an ‘attracting locus’ at infinity, in the sense that:
-
(i) either there exists a superattracting fixed point
 $q\in X\setminus \mathbb{A}^{2}$
such that there is no branch of the curve at
$q\in X\setminus \mathbb{A}^{2}$
such that there is no branch of the curve at
 $q$
which is periodic under
$q$
which is periodic under
 $f$
;
$f$
; -
(ii) or there exists an irreducible component
 $E\in X\setminus \mathbb{A}^{2}$
such that
$E\in X\setminus \mathbb{A}^{2}$
such that
 $f^{\ast }E=dE+F$
, where
$f^{\ast }E=dE+F$
, where
 $d\geqslant 2$
and
$d\geqslant 2$
and
 $F$
is an effective divisor supported by
$F$
is an effective divisor supported by
 $X\setminus \mathbb{A}^{2}$
.
$X\setminus \mathbb{A}^{2}$
.
In Case (i), we can find a point
 $p\in \mathbb{A}^{2}(\bar{\mathbb{Q}})$
near
$p\in \mathbb{A}^{2}(\bar{\mathbb{Q}})$
near
![]() $q$
with respect to the Euclidean topology. Then we have
$q$
with respect to the Euclidean topology. Then we have
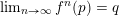 $\lim _{n\rightarrow \infty }f^{n}(p)=q$
. It is easy to show that the orbit of
$\lim _{n\rightarrow \infty }f^{n}(p)=q$
. It is easy to show that the orbit of
![]() $p$
is Zariski dense in
$p$
is Zariski dense in
![]() $\mathbb{A}^{2}$
.
$\mathbb{A}^{2}$
.
In Case (ii),
![]() $E$
is defined over
$E$
is defined over
![]() $\mathbb{Q}$
. There exists a prime number
$\mathbb{Q}$
. There exists a prime number
![]() $\mathfrak{p}\geqslant 3$
such that
$\mathfrak{p}\geqslant 3$
such that
![]() $f_{\mathfrak{p}}|_{E_{\mathfrak{p}}}$
is dominant, where
$f_{\mathfrak{p}}|_{E_{\mathfrak{p}}}$
is dominant, where
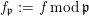 $f_{\mathfrak{p}}:=f\,\text{mod}\,\mathfrak{p}$
and
$f_{\mathfrak{p}}:=f\,\text{mod}\,\mathfrak{p}$
and
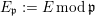 $E_{\mathfrak{p}}:=E\,\text{mod}\,\mathfrak{p}$
.
$E_{\mathfrak{p}}:=E\,\text{mod}\,\mathfrak{p}$
.
We first treat the case
 $f^{n}|_{E}\neq \operatorname{id}$
for all
$f^{n}|_{E}\neq \operatorname{id}$
for all
![]() $n\geqslant 1$
. After replacing
$n\geqslant 1$
. After replacing
![]() $f$
by a suitable iterate, we may find a fixed point
$f$
by a suitable iterate, we may find a fixed point
![]() $x\in E_{\mathfrak{p}}$
such that
$x\in E_{\mathfrak{p}}$
such that
 $df_{\mathfrak{p}}(x)=1$
in
$df_{\mathfrak{p}}(x)=1$
in
![]() $\bar{\mathbb{F}}_{\mathfrak{p}}$
. Denote by
$\bar{\mathbb{F}}_{\mathfrak{p}}$
. Denote by
![]() $U$
the
$U$
the
![]() $\mathfrak{p}$
-adic open set of
$\mathfrak{p}$
-adic open set of
![]() $X(\mathbb{Q}_{\mathfrak{p}})$
consisting of the points
$X(\mathbb{Q}_{\mathfrak{p}})$
consisting of the points
![]() $y$
such that
$y$
such that
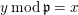 $y\,\text{mod}\,\mathfrak{p}=x$
. Then
$y\,\text{mod}\,\mathfrak{p}=x$
. Then
![]() $U$
is fixed by
$U$
is fixed by
![]() $f$
. By [Reference PoonenPoo14, Theorem 1], all the preperiodic points in
$f$
. By [Reference PoonenPoo14, Theorem 1], all the preperiodic points in
![]() $U\cap E$
are fixed. Moreover,
$U\cap E$
are fixed. Moreover,
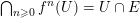 $\bigcap _{n\geqslant 0}f^{n}(U)=U\cap E$
. Denote by
$\bigcap _{n\geqslant 0}f^{n}(U)=U\cap E$
. Denote by
![]() $S$
the set of fixed points in
$S$
the set of fixed points in
![]() $U\cap E$
. Then
$U\cap E$
. Then
![]() $S$
is finite. If
$S$
is finite. If
![]() $S$
is empty, pick a point
$S$
is empty, pick a point
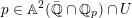 $p\in \mathbb{A}^{2}(\bar{\mathbb{Q}}\cap \mathbb{Q}_{p})\cap U$
; it is easy to see that the orbit of
$p\in \mathbb{A}^{2}(\bar{\mathbb{Q}}\cap \mathbb{Q}_{p})\cap U$
; it is easy to see that the orbit of
![]() $p$
is Zariski dense in
$p$
is Zariski dense in
![]() $\mathbb{A}^{2}$
. If
$\mathbb{A}^{2}$
. If
![]() $S$
is not empty, by [Reference AbateAba01, Theorem 3.1.4], at each point
$S$
is not empty, by [Reference AbateAba01, Theorem 3.1.4], at each point
![]() $q_{i}\in S$
there exists at most one algebraic curve
$q_{i}\in S$
there exists at most one algebraic curve
![]() $C_{i}$
passing through
$C_{i}$
passing through
![]() $q_{i}$
which is preperiodic. Set
$q_{i}$
which is preperiodic. Set
![]() $C_{i}=\emptyset$
if no such curve does exist. We have that
$C_{i}=\emptyset$
if no such curve does exist. We have that
![]() $C_{i}$
is fixed. Pick a point
$C_{i}$
is fixed. Pick a point
 $p\in \mathbb{A}^{2}(\bar{\mathbb{Q}}\cap \mathbb{Q}_{p})\setminus C_{1}$
very close to
$p\in \mathbb{A}^{2}(\bar{\mathbb{Q}}\cap \mathbb{Q}_{p})\setminus C_{1}$
very close to
![]() $q_{1}$
. We can show that the orbit of
$q_{1}$
. We can show that the orbit of
![]() $p$
is Zariski dense in
$p$
is Zariski dense in
![]() $\mathbb{A}^{2}$
.
$\mathbb{A}^{2}$
.
Next, we treat the case
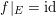 $f|_{E}=\operatorname{id}$
. By [Reference AbateAba01, Theorem 3.1.4], at each point
$f|_{E}=\operatorname{id}$
. By [Reference AbateAba01, Theorem 3.1.4], at each point
![]() $q\in E$
there exists at most one algebraic curve
$q\in E$
there exists at most one algebraic curve
![]() $C_{q}$
passing through
$C_{q}$
passing through
![]() $q$
which is preperiodic. Set
$q$
which is preperiodic. Set
![]() $C_{q}=\emptyset$
if such curve does not exist. We have that
$C_{q}=\emptyset$
if such curve does not exist. We have that
![]() $C_{q}$
is fixed and transverse to
$C_{q}$
is fixed and transverse to
![]() $E$
. If
$E$
. If
![]() $C_{q}=\emptyset$
for all but finitely many
$C_{q}=\emptyset$
for all but finitely many
![]() $q\in E$
, then there exist
$q\in E$
, then there exist
![]() $q\in E$
and a
$q\in E$
and a
![]() $\mathfrak{p}$
-adic neighborhood
$\mathfrak{p}$
-adic neighborhood
![]() $U$
of
$U$
of
![]() $q$
such that for any point
$q$
such that for any point
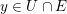 $y\in U\cap E$
,
$y\in U\cap E$
,
![]() $C_{y}=\emptyset$
,
$C_{y}=\emptyset$
,
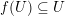 $f(U)\subseteq U$
and
$f(U)\subseteq U$
and
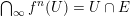 $\bigcap _{\infty }f^{n}(U)=U\cap E$
. Then, for any point
$\bigcap _{\infty }f^{n}(U)=U\cap E$
. Then, for any point
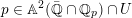 $p\in \mathbb{A}^{2}(\bar{\mathbb{Q}}\cap \mathbb{Q}_{p})\cap U$
, the orbit of
$p\in \mathbb{A}^{2}(\bar{\mathbb{Q}}\cap \mathbb{Q}_{p})\cap U$
, the orbit of
![]() $p$
is Zariski dense in
$p$
is Zariski dense in
![]() $\mathbb{A}^{2}$
. Otherwise there exists a sequence of points
$\mathbb{A}^{2}$
. Otherwise there exists a sequence of points
![]() $q_{i}\in E$
such that
$q_{i}\in E$
such that
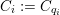 $C_{i}:=C_{q_{i}}$
is an irreducible curve. Since
$C_{i}:=C_{q_{i}}$
is an irreducible curve. Since
![]() $f|_{C_{i}}$
is an endomorphism of
$f|_{C_{i}}$
is an endomorphism of
![]() $C_{i}\cap \mathbb{A}^{2}$
of degree at least
$C_{i}\cap \mathbb{A}^{2}$
of degree at least
![]() $2$
,
$2$
,
![]() $C_{i}$
has at most two branches at infinity. Since
$C_{i}$
has at most two branches at infinity. Since
![]() $C_{i}$
is transverse to
$C_{i}$
is transverse to
![]() $E$
at
$E$
at
![]() $q_{i}$
, we can bound the intersection number
$q_{i}$
, we can bound the intersection number
![]() $(E\cdot C_{i})$
. By the technique developed in [Reference XieXie15a], we can also bound the intersection of
$(E\cdot C_{i})$
. By the technique developed in [Reference XieXie15a], we can also bound the intersection of
![]() $C_{i}$
with the other irreducible components of
$C_{i}$
with the other irreducible components of
![]() $X\setminus \mathbb{A}^{2}$
. Then we bound the degree of
$X\setminus \mathbb{A}^{2}$
. Then we bound the degree of
![]() $C_{i}$
, which allows us to construct a nonconstant invariant rational function.
$C_{i}$
, which allows us to construct a nonconstant invariant rational function.
The article is organized in two parts.
In Part I, we gather some results on the geometry and dynamics at infinity and metrics on projective varieties defined over a valued field. We first introduce the valuative tree at infinity in § 2, and then we recall the main properties of the action of a polynomial map on the valuation space in § 3. Next, we introduce the Green function on the valuative tree for a polynomial endomorphism in § 4. Finally, we give background information on metrics on projective varieties defined over a valued field in § 5.
In Part II, we prove Theorem 1.1. We first prove it in some special cases in § 6. In most of these cases, we find a Zariski dense orbit in some attracting locus. Then we study totally invariant curves in § 7 and prove Theorem 1.1 when there are infinitely many such curves. Finally, we finish the proof of Theorem 1.1 in § 8.
Part I. Preliminaries
In this part, we denote by
![]() $k$
an algebraically closed field of characteristic
$k$
an algebraically closed field of characteristic
![]() $0$
. We also fix affine coordinates on
$0$
. We also fix affine coordinates on
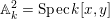 $\mathbb{A}_{k}^{2}=\operatorname{Spec}k[x,y]$
.
$\mathbb{A}_{k}^{2}=\operatorname{Spec}k[x,y]$
.
2 The valuative tree at infinity
We refer to [Reference Jonsson, Nicaise, Ducros and FavreJon15] for details; see also [Reference Favre and JonssonFJ04, Reference Favre and JonssonFJ07, Reference Favre and JonssonFJ11].
2.1 The valuative tree at infinity
In this article by a valuation on a unitary
![]() $k$
-algebra
$k$
-algebra
![]() $R$
we shall understand a function
$R$
we shall understand a function
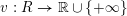 $v:R\rightarrow \mathbb{R}\cup \{+\infty \}$
such that the restriction of
$v:R\rightarrow \mathbb{R}\cup \{+\infty \}$
such that the restriction of
![]() $v$
to
$v$
to
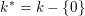 $k^{\ast }=k-\{0\}$
is constant equal to
$k^{\ast }=k-\{0\}$
is constant equal to
![]() $0$
, and
$0$
, and
![]() $v$
satisfies
$v$
satisfies
 $v(fg)=v(f)+v(g)$
and
$v(fg)=v(f)+v(g)$
and
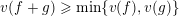 $v(f+g)\geqslant \min \{v(f),v(g)\}$
. It is usually referred to as a semivaluation in the literature; see [Reference Favre and JonssonFJ04]. We will however make a slight abuse of notation and call it a valuation.
$v(f+g)\geqslant \min \{v(f),v(g)\}$
. It is usually referred to as a semivaluation in the literature; see [Reference Favre and JonssonFJ04]. We will however make a slight abuse of notation and call it a valuation.
Denote by
![]() $V_{\infty }$
the space of all normalized valuations centered at infinity, i.e. the set of valuations
$V_{\infty }$
the space of all normalized valuations centered at infinity, i.e. the set of valuations
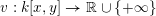 $v:k[x,y]\rightarrow \mathbb{R}\cup \{+\infty \}$
satisfying
$v:k[x,y]\rightarrow \mathbb{R}\cup \{+\infty \}$
satisfying
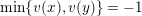 $\min \{v(x),v(y)\}=-1$
. The topology on
$\min \{v(x),v(y)\}=-1$
. The topology on
![]() $V_{\infty }$
is defined to be the weakest topology making the map
$V_{\infty }$
is defined to be the weakest topology making the map
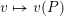 $v\mapsto v(P)$
continuous for every
$v\mapsto v(P)$
continuous for every
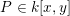 $P\in k[x,y]$
.
$P\in k[x,y]$
.
The set
![]() $V_{\infty }$
is equipped with a partial ordering defined by
$V_{\infty }$
is equipped with a partial ordering defined by
![]() $v\leqslant w$
if and only if
$v\leqslant w$
if and only if
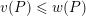 $v(P)\leqslant w(P)$
for all
$v(P)\leqslant w(P)$
for all
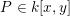 $P\in k[x,y]$
. Then
$P\in k[x,y]$
. Then
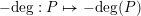 $-\text{deg}:P\mapsto -\text{deg}(P)$
is the unique minimal element.
$-\text{deg}:P\mapsto -\text{deg}(P)$
is the unique minimal element.
Given any valuation
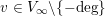 $v\in V_{\infty }\setminus \{-\text{deg}\}$
, the set
$v\in V_{\infty }\setminus \{-\text{deg}\}$
, the set
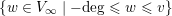 $\{w\in V_{\infty }\mid -\text{deg}\leqslant w\leqslant v\}$
is isomorphic as a poset to the real segment
$\{w\in V_{\infty }\mid -\text{deg}\leqslant w\leqslant v\}$
is isomorphic as a poset to the real segment
![]() $[0,1]$
endowed with the standard ordering. In other words,
$[0,1]$
endowed with the standard ordering. In other words,
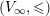 $(V_{\infty },\leqslant )$
is a rooted tree in the sense of [Reference Favre and JonssonFJ04, Reference Jonsson, Nicaise, Ducros and FavreJon15].
$(V_{\infty },\leqslant )$
is a rooted tree in the sense of [Reference Favre and JonssonFJ04, Reference Jonsson, Nicaise, Ducros and FavreJon15].
Given any two valuations
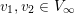 $v_{1},v_{2}\in V_{\infty }$
, there is a unique valuation in
$v_{1},v_{2}\in V_{\infty }$
, there is a unique valuation in
![]() $V_{\infty }$
which is maximal in the set
$V_{\infty }$
which is maximal in the set
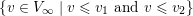 $\{v\in V_{\infty }\mid v\leqslant v_{1}\text{ and }v\leqslant v_{2}\}$
. We denote it by
$\{v\in V_{\infty }\mid v\leqslant v_{1}\text{ and }v\leqslant v_{2}\}$
. We denote it by
![]() $v_{1}\wedge v_{2}$
.
$v_{1}\wedge v_{2}$
.
The segment
![]() $[v_{1},v_{2}]$
is by definition the union of
$[v_{1},v_{2}]$
is by definition the union of
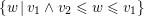 $\{w\,|\,v_{1}\wedge v_{2}\leqslant w\leqslant v_{1}\}$
and
$\{w\,|\,v_{1}\wedge v_{2}\leqslant w\leqslant v_{1}\}$
and
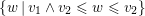 $\{w\,|\,v_{1}\wedge v_{2}\leqslant w\leqslant v_{2}\}$
.
$\{w\,|\,v_{1}\wedge v_{2}\leqslant w\leqslant v_{2}\}$
.
Pick any valuation
![]() $v\in V_{\infty }$
. We say that two points
$v\in V_{\infty }$
. We say that two points
![]() $v_{1},v_{2}$
lie in the same direction at
$v_{1},v_{2}$
lie in the same direction at
![]() $v$
if the segment
$v$
if the segment
![]() $[v_{1},v_{2}]$
does not contain
$[v_{1},v_{2}]$
does not contain
![]() $v$
. A direction (or a tangent vector) at
$v$
. A direction (or a tangent vector) at
![]() $v$
is an equivalence class for this relation. We write
$v$
is an equivalence class for this relation. We write
![]() $\operatorname{Tan}_{v}$
for the set of directions at
$\operatorname{Tan}_{v}$
for the set of directions at
![]() $v$
.
$v$
.
When
![]() $\operatorname{Tan}_{v}$
is a singleton, then
$\operatorname{Tan}_{v}$
is a singleton, then
![]() $v$
is called an end point. In
$v$
is called an end point. In
![]() $V_{\infty }$
, the set of end points is exactly the set of all maximal valuations. When
$V_{\infty }$
, the set of end points is exactly the set of all maximal valuations. When
![]() $\operatorname{Tan}_{v}$
contains exactly two directions, then
$\operatorname{Tan}_{v}$
contains exactly two directions, then
![]() $v$
is said to be regular. When
$v$
is said to be regular. When
![]() $\operatorname{Tan}_{v}$
has more than three directions, then
$\operatorname{Tan}_{v}$
has more than three directions, then
![]() $v$
is a branch point.
$v$
is a branch point.
Pick any
![]() $v\in V_{\infty }$
. For any tangent vector
$v\in V_{\infty }$
. For any tangent vector
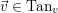 $\vec{v}\in \operatorname{Tan}_{v}$
, denote by
$\vec{v}\in \operatorname{Tan}_{v}$
, denote by
![]() $U(\vec{v})$
the subset of those elements in
$U(\vec{v})$
the subset of those elements in
![]() $V_{\infty }$
that determine
$V_{\infty }$
that determine
![]() $\vec{v}$
. This is an open set whose boundary is reduced to the singleton
$\vec{v}$
. This is an open set whose boundary is reduced to the singleton
![]() $\{v\}$
. If
$\{v\}$
. If
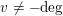 $v\neq -\text{deg}$
, the complement of
$v\neq -\text{deg}$
, the complement of
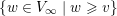 $\{w\in V_{\infty }\mid w\geqslant v\}$
is equal to
$\{w\in V_{\infty }\mid w\geqslant v\}$
is equal to
![]() $U(\vec{v}_{0})$
, where
$U(\vec{v}_{0})$
, where
![]() $\vec{v}_{0}$
is the tangent vector determined by
$\vec{v}_{0}$
is the tangent vector determined by
![]() $-\text{deg}$
.
$-\text{deg}$
.
It is a fact that finite intersections of open sets of the form
![]() $U(\vec{v})$
form a basis for the topology of
$U(\vec{v})$
form a basis for the topology of
![]() $V_{\infty }$
.
$V_{\infty }$
.
2.2 Compactifications of
 $\mathbb{A}_{k}^{2}$
$\mathbb{A}_{k}^{2}$
A compactification of
![]() $\mathbb{A}_{k}^{2}$
is the data of a projective surface
$\mathbb{A}_{k}^{2}$
is the data of a projective surface
![]() $X$
together with an open immersion
$X$
together with an open immersion
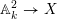 $\mathbb{A}_{k}^{2}\rightarrow X$
with dense image.
$\mathbb{A}_{k}^{2}\rightarrow X$
with dense image.
A compactification
![]() $X$
dominates another one
$X$
dominates another one
![]() $X^{\prime }$
if the canonical birational map
$X^{\prime }$
if the canonical birational map
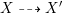 $X{\dashrightarrow}X^{\prime }$
induced by the inclusion of
$X{\dashrightarrow}X^{\prime }$
induced by the inclusion of
![]() $\mathbb{A}_{k}^{2}$
in both surfaces is in fact a regular map.
$\mathbb{A}_{k}^{2}$
in both surfaces is in fact a regular map.
The category
![]() ${\mathcal{C}}$
of all compactifications of
${\mathcal{C}}$
of all compactifications of
![]() $\mathbb{A}_{k}^{2}$
forms an inductive system for the relation of domination.
$\mathbb{A}_{k}^{2}$
forms an inductive system for the relation of domination.
Recall that we have fixed affine coordinates on
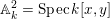 $\mathbb{A}_{k}^{2}=\operatorname{Spec}k[x,y]$
. We let
$\mathbb{A}_{k}^{2}=\operatorname{Spec}k[x,y]$
. We let
![]() $\mathbb{P}_{k}^{2}$
be the standard compactification of
$\mathbb{P}_{k}^{2}$
be the standard compactification of
![]() $\mathbb{A}_{k}^{2}$
and denote by
$\mathbb{A}_{k}^{2}$
and denote by
 $l_{\infty }:=\mathbb{P}_{k}^{2}\setminus \mathbb{A}_{k}^{2}$
the line at infinity in the projective plane.
$l_{\infty }:=\mathbb{P}_{k}^{2}\setminus \mathbb{A}_{k}^{2}$
the line at infinity in the projective plane.
An admissible compactification of
![]() $\mathbb{A}_{k}^{2}$
is by definition a smooth projective surface
$\mathbb{A}_{k}^{2}$
is by definition a smooth projective surface
![]() $X$
endowed with a birational morphism
$X$
endowed with a birational morphism
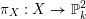 $\unicode[STIX]{x1D70B}_{X}:X\rightarrow \mathbb{P}_{k}^{2}$
such that
$\unicode[STIX]{x1D70B}_{X}:X\rightarrow \mathbb{P}_{k}^{2}$
such that
![]() $\unicode[STIX]{x1D70B}_{X}$
is an isomorphism over
$\unicode[STIX]{x1D70B}_{X}$
is an isomorphism over
![]() $\mathbb{A}_{k}^{2}$
with the embedding
$\mathbb{A}_{k}^{2}$
with the embedding
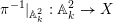 $\unicode[STIX]{x1D70B}^{-1}|_{\mathbb{A}_{k}^{2}}:\mathbb{A}_{k}^{2}\rightarrow X$
. Recall that
$\unicode[STIX]{x1D70B}^{-1}|_{\mathbb{A}_{k}^{2}}:\mathbb{A}_{k}^{2}\rightarrow X$
. Recall that
![]() $\unicode[STIX]{x1D70B}_{X}$
can then be decomposed as a finite sequence of point blow-ups.
$\unicode[STIX]{x1D70B}_{X}$
can then be decomposed as a finite sequence of point blow-ups.
We shall denote by
![]() ${\mathcal{C}}_{0}$
the category of all admissible compactifications. It is also an inductive system for the relation of domination. Moreover,
${\mathcal{C}}_{0}$
the category of all admissible compactifications. It is also an inductive system for the relation of domination. Moreover,
![]() ${\mathcal{C}}_{0}$
is a subcategory of
${\mathcal{C}}_{0}$
is a subcategory of
![]() ${\mathcal{C}}$
and, for any compactification
${\mathcal{C}}$
and, for any compactification
![]() $X\in {\mathcal{C}}$
, there exists
$X\in {\mathcal{C}}$
, there exists
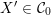 $X^{\prime }\in {\mathcal{C}}_{0}$
that dominates
$X^{\prime }\in {\mathcal{C}}_{0}$
that dominates
![]() $X$
.
$X$
.
2.3 Divisorial valuations
Let
![]() $X\in {\mathcal{C}}$
be a compactification of
$X\in {\mathcal{C}}$
be a compactification of
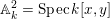 $\mathbb{A}_{k}^{2}=\operatorname{Spec}k[x,y]$
and
$\mathbb{A}_{k}^{2}=\operatorname{Spec}k[x,y]$
and
![]() $E$
be an irreducible component of
$E$
be an irreducible component of
![]() $X\setminus \mathbb{A}^{2}$
. Set
$X\setminus \mathbb{A}^{2}$
. Set
 $b_{E}:=-\text{min}\{\operatorname{ord}_{E}(x),\operatorname{ord}_{E}(y)\}$
and
$b_{E}:=-\text{min}\{\operatorname{ord}_{E}(x),\operatorname{ord}_{E}(y)\}$
and
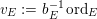 $v_{E}:=b_{E}^{-1}\operatorname{ord}_{E}$
. Then we have
$v_{E}:=b_{E}^{-1}\operatorname{ord}_{E}$
. Then we have
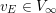 $v_{E}\in V_{\infty }$
.
$v_{E}\in V_{\infty }$
.
By Poincaré duality, there exists a unique dual divisor
![]() ${\check{E}}$
of
${\check{E}}$
of
![]() $E$
defined as the unique divisor supported on
$E$
defined as the unique divisor supported on
![]() $X\setminus \mathbb{A}^{2}$
such that
$X\setminus \mathbb{A}^{2}$
such that
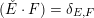 $({\check{E}}\cdot F)=\unicode[STIX]{x1D6FF}_{E,F}$
for all irreducible components
$({\check{E}}\cdot F)=\unicode[STIX]{x1D6FF}_{E,F}$
for all irreducible components
![]() $F$
of
$F$
of
![]() $X\setminus \mathbb{A}^{2}$
.
$X\setminus \mathbb{A}^{2}$
.
Remark 2.1. Recall that
![]() $l_{\infty }$
is the line at infinity of
$l_{\infty }$
is the line at infinity of
![]() $\mathbb{P}^{2}$
. Let
$\mathbb{P}^{2}$
. Let
![]() $s$
be a formal curve centered at some point
$s$
be a formal curve centered at some point
![]() $q\in l_{\infty }$
. Suppose that the strict transform of
$q\in l_{\infty }$
. Suppose that the strict transform of
![]() $s$
in
$s$
in
![]() $X$
intersects
$X$
intersects
![]() $E$
transversally at a point in
$E$
transversally at a point in
![]() $E$
which is smooth in
$E$
which is smooth in
![]() $X\setminus \mathbb{A}^{2}$
. Then we have
$X\setminus \mathbb{A}^{2}$
. Then we have
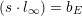 $(s\cdot l_{\infty })=b_{E}$
.
$(s\cdot l_{\infty })=b_{E}$
.
2.4 Classification of valuations
There are four kinds of valuations in
![]() $V_{\infty }$
. The first one corresponds to the divisorial valuations which we have defined above. We now describe the three remaining types of valuations.
$V_{\infty }$
. The first one corresponds to the divisorial valuations which we have defined above. We now describe the three remaining types of valuations.
Irrational valuations
Consider any two irreducible components
![]() $E$
and
$E$
and
![]() $E^{\prime }$
of
$E^{\prime }$
of
![]() $X\setminus \mathbb{A}_{k}^{2}$
for some compactification
$X\setminus \mathbb{A}_{k}^{2}$
for some compactification
![]() $X\in {\mathcal{C}}$
of
$X\in {\mathcal{C}}$
of
![]() $\mathbb{A}_{k}^{2}$
intersecting at a point
$\mathbb{A}_{k}^{2}$
intersecting at a point
![]() $p$
. There exists local coordinates
$p$
. There exists local coordinates
![]() $(z,w)$
at
$(z,w)$
at
![]() $p$
such that
$p$
such that
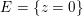 $E=\{z=0\}$
and
$E=\{z=0\}$
and
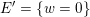 $E^{\prime }=\{w=0\}$
. To any pair
$E^{\prime }=\{w=0\}$
. To any pair
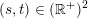 $(s,t)\in (\mathbb{R}^{+})^{2}$
satisfying
$(s,t)\in (\mathbb{R}^{+})^{2}$
satisfying
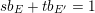 $sb_{E}+tb_{E^{\prime }}=1$
, we attach the valuation
$sb_{E}+tb_{E^{\prime }}=1$
, we attach the valuation
![]() $v$
defined on the ring
$v$
defined on the ring
![]() $O_{p}$
of germs at
$O_{p}$
of germs at
![]() $p$
by
$p$
by
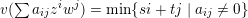 $v(\sum a_{ij}z^{i}w^{j})=\min \{si+tj\mid a_{ij}\neq 0\}$
. Observe that it does not depend on the choice of coordinates. By first extending
$v(\sum a_{ij}z^{i}w^{j})=\min \{si+tj\mid a_{ij}\neq 0\}$
. Observe that it does not depend on the choice of coordinates. By first extending
![]() $v$
to the common fraction field
$v$
to the common fraction field
![]() $k(x,y)$
of
$k(x,y)$
of
![]() $O_{p}$
and
$O_{p}$
and
![]() $k[x,y]$
and then restricting it to
$k[x,y]$
and then restricting it to
![]() $k[x,y]$
, we obtain a valuation in
$k[x,y]$
, we obtain a valuation in
![]() $V_{\infty }$
, called quasimonomial. It is divisorial if and only if either
$V_{\infty }$
, called quasimonomial. It is divisorial if and only if either
![]() $t=0$
or the ratio
$t=0$
or the ratio
![]() $s/t$
is a rational number. Any divisorial valuation is quasimonomial. An irrational valuation is by definition a nondivisorial quasimonomial valuation.
$s/t$
is a rational number. Any divisorial valuation is quasimonomial. An irrational valuation is by definition a nondivisorial quasimonomial valuation.
Curve valuations
Recall that
![]() $l_{\infty }$
is the line at infinity of
$l_{\infty }$
is the line at infinity of
![]() $\mathbb{P}_{k}^{2}$
. For any formal curve
$\mathbb{P}_{k}^{2}$
. For any formal curve
![]() $s$
centered at some point
$s$
centered at some point
![]() $q\in l_{\infty }$
, denote by
$q\in l_{\infty }$
, denote by
![]() $v_{s}$
the valuation defined by
$v_{s}$
the valuation defined by
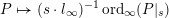 $P\mapsto (s\cdot l_{\infty })^{-1}\operatorname{ord}_{\infty }(P|_{s})$
. Then we have
$P\mapsto (s\cdot l_{\infty })^{-1}\operatorname{ord}_{\infty }(P|_{s})$
. Then we have
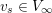 $v_{s}\in V_{\infty }$
and we call it a curve valuation.
$v_{s}\in V_{\infty }$
and we call it a curve valuation.
Let
![]() $C$
be an irreducible curve in
$C$
be an irreducible curve in
![]() $\mathbb{P}_{k}^{2}$
. For any point
$\mathbb{P}_{k}^{2}$
. For any point
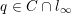 $q\in C\cap l_{\infty }$
, denote by
$q\in C\cap l_{\infty }$
, denote by
![]() $O_{q}$
the local ring at
$O_{q}$
the local ring at
![]() $q$
,
$q$
,
![]() $m_{q}$
the maximal ideal of
$m_{q}$
the maximal ideal of
![]() $O_{q}$
and
$O_{q}$
and
![]() $I_{C}$
the ideal of height 1 in
$I_{C}$
the ideal of height 1 in
![]() $O_{q}$
defined by
$O_{q}$
defined by
![]() $C$
. Denote by
$C$
. Denote by
![]() $\widehat{O}_{q}$
the completion of
$\widehat{O}_{q}$
the completion of
![]() $O_{q}$
with respect to
$O_{q}$
with respect to
![]() $m_{q}$
,
$m_{q}$
,
![]() $\widehat{m}_{q}$
the completion of
$\widehat{m}_{q}$
the completion of
![]() $m_{q}$
and
$m_{q}$
and
![]() $\widehat{I}_{C}$
the completion of
$\widehat{I}_{C}$
the completion of
![]() $I_{C}$
. For any prime ideal
$I_{C}$
. For any prime ideal
![]() $\widehat{p}$
of height 1 containing
$\widehat{p}$
of height 1 containing
![]() $\widehat{I}_{C}$
, the morphism
$\widehat{I}_{C}$
, the morphism
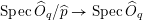 $\operatorname{Spec}\widehat{O}_{q}/\widehat{p}\rightarrow \operatorname{Spec}\widehat{O}_{q}$
defines a formal curve centered at
$\operatorname{Spec}\widehat{O}_{q}/\widehat{p}\rightarrow \operatorname{Spec}\widehat{O}_{q}$
defines a formal curve centered at
![]() $q$
. Such a formal curve is called a branch of
$q$
. Such a formal curve is called a branch of
![]() $C$
at infinity.
$C$
at infinity.
Infinitely singular valuations
Let
![]() $h$
be a formal series of the form
$h$
be a formal series of the form
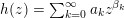 $h(z)=\sum _{k=0}^{\infty }a_{k}z^{\unicode[STIX]{x1D6FD}_{k}}$
with
$h(z)=\sum _{k=0}^{\infty }a_{k}z^{\unicode[STIX]{x1D6FD}_{k}}$
with
![]() $a_{k}\in k^{\ast }$
and
$a_{k}\in k^{\ast }$
and
![]() $\{\unicode[STIX]{x1D6FD}\}_{k}$
an increasing sequence of rational numbers with unbounded denominators. Then
$\{\unicode[STIX]{x1D6FD}\}_{k}$
an increasing sequence of rational numbers with unbounded denominators. Then
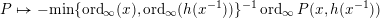 $P\mapsto -\text{min}\{\operatorname{ord}_{\infty }(x),\operatorname{ord}_{\infty }(h(x^{-1}))\}^{-1}\operatorname{ord}_{\infty }P(x,h(x^{-1}))$
defines a valuation in
$P\mapsto -\text{min}\{\operatorname{ord}_{\infty }(x),\operatorname{ord}_{\infty }(h(x^{-1}))\}^{-1}\operatorname{ord}_{\infty }P(x,h(x^{-1}))$
defines a valuation in
![]() $V_{\infty }$
called an infinitely singular valuation.
$V_{\infty }$
called an infinitely singular valuation.
A valuation
![]() $v\in V_{\infty }$
is a branch point in
$v\in V_{\infty }$
is a branch point in
![]() $V_{\infty }$
if and only if it is divisorial, it is a regular point in
$V_{\infty }$
if and only if it is divisorial, it is a regular point in
![]() $V_{\infty }$
if and only if it is an irrational valuation and it is an end point in
$V_{\infty }$
if and only if it is an irrational valuation and it is an end point in
![]() $V_{\infty }$
if and only if it is a curve valuation or an infinitely singular valuation. Moreover, given any smooth projective compactification
$V_{\infty }$
if and only if it is a curve valuation or an infinitely singular valuation. Moreover, given any smooth projective compactification
![]() $X$
in which
$X$
in which
![]() $v=v_{E}$
, one proves that the map sending an element
$v=v_{E}$
, one proves that the map sending an element
![]() $V_{\infty }$
to its center in
$V_{\infty }$
to its center in
![]() $X$
induces a map
$X$
induces a map
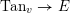 $\operatorname{Tan}_{v}\rightarrow E$
that is a bijection.
$\operatorname{Tan}_{v}\rightarrow E$
that is a bijection.
2.5 Parameterizations
The skewness function
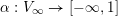 $\unicode[STIX]{x1D6FC}:V_{\infty }\rightarrow [-\infty ,1]$
is the unique function on
$\unicode[STIX]{x1D6FC}:V_{\infty }\rightarrow [-\infty ,1]$
is the unique function on
![]() $V_{\infty }$
that is continuous on segments and satisfies
$V_{\infty }$
that is continuous on segments and satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}(v_{E})=\frac{1}{b_{E}^{2}}({\check{E}}\cdot {\check{E}}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}(v_{E})=\frac{1}{b_{E}^{2}}({\check{E}}\cdot {\check{E}}),\end{eqnarray}$$
where
![]() $E$
is any irreducible component of
$E$
is any irreducible component of
![]() $X\setminus \mathbb{A}_{k}^{2}$
of any compactification
$X\setminus \mathbb{A}_{k}^{2}$
of any compactification
![]() $X$
of
$X$
of
![]() $\mathbb{A}_{k}^{2}$
and
$\mathbb{A}_{k}^{2}$
and
![]() ${\check{E}}$
is the dual divisor of
${\check{E}}$
is the dual divisor of
![]() $E$
as defined above.
$E$
as defined above.
The skewness function is strictly decreasing and upper semicontinuous. In an analogous way, one defines the thinness function
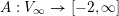 $A:V_{\infty }\rightarrow [-2,\infty ]$
as the unique, increasing, lower semicontinuous function on
$A:V_{\infty }\rightarrow [-2,\infty ]$
as the unique, increasing, lower semicontinuous function on
![]() $V_{\infty }$
such that for any irreducible exceptional divisor
$V_{\infty }$
such that for any irreducible exceptional divisor
![]() $E$
in some compactification
$E$
in some compactification
![]() $X\in {\mathcal{C}}$
, we have
$X\in {\mathcal{C}}$
, we have
 $$\begin{eqnarray}A(v_{E})=\frac{1}{b_{E}}\,(1+\operatorname{ord}_{E}(dx\wedge dy)).\end{eqnarray}$$
$$\begin{eqnarray}A(v_{E})=\frac{1}{b_{E}}\,(1+\operatorname{ord}_{E}(dx\wedge dy)).\end{eqnarray}$$
Here we extend the differential form
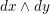 $dx\wedge dy$
to a rational differential form on
$dx\wedge dy$
to a rational differential form on
![]() $X$
.
$X$
.
2.6 Computation of local intersection numbers of curves at infinity
Let
![]() $s_{1}$
,
$s_{1}$
,
![]() $s_{2}$
be two different formal curves at infinity. We denote by
$s_{2}$
be two different formal curves at infinity. We denote by
![]() $(s_{1}\cdot s_{2})$
the intersection number of these two formal curves in
$(s_{1}\cdot s_{2})$
the intersection number of these two formal curves in
![]() $\mathbb{P}^{2}$
. This intersection number is always nonnegative, and it is positive if and only if
$\mathbb{P}^{2}$
. This intersection number is always nonnegative, and it is positive if and only if
![]() $s_{1}$
and
$s_{1}$
and
![]() $s_{2}$
are centered at the same point.
$s_{2}$
are centered at the same point.
Denote by
![]() $l_{\infty }$
the line at infinity in
$l_{\infty }$
the line at infinity in
![]() $\mathbb{P}_{k}^{2}$
. Denote by
$\mathbb{P}_{k}^{2}$
. Denote by
![]() $v_{s_{1}},v_{s_{2}}$
the curve valuations associated to
$v_{s_{1}},v_{s_{2}}$
the curve valuations associated to
![]() $s_{1}$
and
$s_{1}$
and
![]() $s_{2}$
.
$s_{2}$
.
By [Reference XieXie15a, Proposition 2.2], we have
 $$\begin{eqnarray}(s_{1}\cdot s_{2})=(s_{1}\cdot l_{\infty })(s_{2}\cdot l_{\infty })(1-\unicode[STIX]{x1D6FC}(v_{s_{1}}\wedge v_{s_{2}})).\end{eqnarray}$$
$$\begin{eqnarray}(s_{1}\cdot s_{2})=(s_{1}\cdot l_{\infty })(s_{2}\cdot l_{\infty })(1-\unicode[STIX]{x1D6FC}(v_{s_{1}}\wedge v_{s_{2}})).\end{eqnarray}$$
3 Background on dynamics of polynomial maps
Recall that the affine coordinates have been fixed,
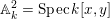 $\mathbb{A}_{k}^{2}=\operatorname{Spec}k[x,y]$
.
$\mathbb{A}_{k}^{2}=\operatorname{Spec}k[x,y]$
.
3.1 Dynamical invariants of polynomial mappings
The (algebraic) degree of a dominant polynomial endomorphism
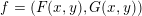 $f=(F(x,y),G(x,y))$
defined on
$f=(F(x,y),G(x,y))$
defined on
![]() $\mathbb{A}_{k}^{2}$
is defined by
$\mathbb{A}_{k}^{2}$
is defined by
 $$\begin{eqnarray}\operatorname{deg}(f):=\max \{\operatorname{deg}(F),\operatorname{deg}(G)\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{deg}(f):=\max \{\operatorname{deg}(F),\operatorname{deg}(G)\}.\end{eqnarray}$$
It is not difficult to show that the sequence
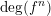 $\operatorname{deg}(f^{n})$
is submultiplicative, so that the limit
$\operatorname{deg}(f^{n})$
is submultiplicative, so that the limit
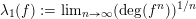 $\unicode[STIX]{x1D706}_{1}(f):=\lim _{n\rightarrow \infty }(\operatorname{deg}(f^{n}))^{1/n}$
exists. It is referred to as the dynamical degree of
$\unicode[STIX]{x1D706}_{1}(f):=\lim _{n\rightarrow \infty }(\operatorname{deg}(f^{n}))^{1/n}$
exists. It is referred to as the dynamical degree of
![]() $f$
, and it is a theorem of Favre and Jonsson that
$f$
, and it is a theorem of Favre and Jonsson that
![]() $\unicode[STIX]{x1D706}_{1}(f)$
is always a quadratic integer; see [Reference Favre and JonssonFJ11].
$\unicode[STIX]{x1D706}_{1}(f)$
is always a quadratic integer; see [Reference Favre and JonssonFJ11].
The (topological) degree
![]() $\unicode[STIX]{x1D706}_{2}(f)$
of
$\unicode[STIX]{x1D706}_{2}(f)$
of
![]() $f$
is defined to be the number of preimages of a general closed point in
$f$
is defined to be the number of preimages of a general closed point in
![]() $\mathbb{A}^{2}(k)$
; one has
$\mathbb{A}^{2}(k)$
; one has
 $\unicode[STIX]{x1D706}_{2}(fg)=\unicode[STIX]{x1D706}_{2}(f)\unicode[STIX]{x1D706}_{2}(g)$
.
$\unicode[STIX]{x1D706}_{2}(fg)=\unicode[STIX]{x1D706}_{2}(f)\unicode[STIX]{x1D706}_{2}(g)$
.
It follows from Bézout’s theorem that
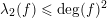 $\unicode[STIX]{x1D706}_{2}(f)\leqslant \operatorname{deg}(f)^{2}$
and hence
$\unicode[STIX]{x1D706}_{2}(f)\leqslant \operatorname{deg}(f)^{2}$
and hence
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}(f)^{2}\geqslant \unicode[STIX]{x1D706}_{2}(f).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{1}(f)^{2}\geqslant \unicode[STIX]{x1D706}_{2}(f).\end{eqnarray}$$
The resonant case
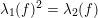 $\unicode[STIX]{x1D706}_{1}(f)^{2}=\unicode[STIX]{x1D706}_{2}(f)$
is quite special and the following structure theorem for these maps is proven in [Reference Favre and JonssonFJ11].
$\unicode[STIX]{x1D706}_{1}(f)^{2}=\unicode[STIX]{x1D706}_{2}(f)$
is quite special and the following structure theorem for these maps is proven in [Reference Favre and JonssonFJ11].
Theorem 3.1. Any polynomial endomorphism
![]() $f$
of
$f$
of
![]() $\mathbb{A}_{k}^{2}$
such that
$\mathbb{A}_{k}^{2}$
such that
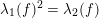 $\unicode[STIX]{x1D706}_{1}(f)^{2}=\unicode[STIX]{x1D706}_{2}(f)$
is proper,Footnote
2
and we are in exactly one of the following two exclusive cases.
$\unicode[STIX]{x1D706}_{1}(f)^{2}=\unicode[STIX]{x1D706}_{2}(f)$
is proper,Footnote
2
and we are in exactly one of the following two exclusive cases.
-
(1)
 $\operatorname{deg}(f^{n})\asymp \unicode[STIX]{x1D706}_{1}(f)^{n}$
; there exists a compactification
$\operatorname{deg}(f^{n})\asymp \unicode[STIX]{x1D706}_{1}(f)^{n}$
; there exists a compactification
 $X$
of
$X$
of
 $\mathbb{A}_{k}^{2}$
to which
$\mathbb{A}_{k}^{2}$
to which
 $f$
extends as a regular map
$f$
extends as a regular map
 $f:X\rightarrow X$
.
$f:X\rightarrow X$
. -
(2)
 $\operatorname{deg}(f^{n})\asymp n\unicode[STIX]{x1D706}_{1}(f)^{n}$
; there exist affine coordinates
$\operatorname{deg}(f^{n})\asymp n\unicode[STIX]{x1D706}_{1}(f)^{n}$
; there exist affine coordinates
 $x,y$
in which
$x,y$
in which
 $f$
takes the form where
$f$
takes the form where $$\begin{eqnarray}f(x,y)=(x^{l}+a_{1}x^{l-1}+\cdots +a_{l},A_{0}(x)y^{l}+\cdots +A_{l}(x)),\end{eqnarray}$$
$$\begin{eqnarray}f(x,y)=(x^{l}+a_{1}x^{l-1}+\cdots +a_{l},A_{0}(x)y^{l}+\cdots +A_{l}(x)),\end{eqnarray}$$
 $a_{i}\in k$
and
$a_{i}\in k$
and
 $A_{i}\in k[x]$
with
$A_{i}\in k[x]$
with
 $\operatorname{deg}A_{0}\geqslant 1$
, and
$\operatorname{deg}A_{0}\geqslant 1$
, and
 $l=\unicode[STIX]{x1D706}_{1}(f)$
.
$l=\unicode[STIX]{x1D706}_{1}(f)$
.
Remark 3.2. Regular endomorphisms as in (1) have been classified in [Reference Favre and JonssonFJ11].
3.2 Valuative dynamics
Any dominant polynomial endomorphism
![]() $f$
as in the previous section induces a natural map on the space of valuations at infinity in the following way.
$f$
as in the previous section induces a natural map on the space of valuations at infinity in the following way.
For any
![]() $v\in V_{\infty }$
, we set
$v\in V_{\infty }$
, we set
 $$\begin{eqnarray}d(f,v):=-\text{min}\{v(F),v(G),0\}\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}d(f,v):=-\text{min}\{v(F),v(G),0\}\geqslant 0.\end{eqnarray}$$
In this way, we get a nonnegative continuous decreasing function on
![]() $V_{\infty }$
. Observe that
$V_{\infty }$
. Observe that
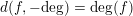 $d(f,-\text{deg})=\operatorname{deg}(f)$
. It is a fact that
$d(f,-\text{deg})=\operatorname{deg}(f)$
. It is a fact that
![]() $f$
is proper if and only if
$f$
is proper if and only if
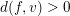 $d(f,v)>0$
for all
$d(f,v)>0$
for all
![]() $v\in V_{\infty }$
.
$v\in V_{\infty }$
.
We now set:
-
∙
 $f_{\ast }v:=0$
if
$f_{\ast }v:=0$
if
 $d(f,v)=0$
;
$d(f,v)=0$
; -
∙
 $f_{\ast }v(P)=v(f^{\ast }P)$
if
$f_{\ast }v(P)=v(f^{\ast }P)$
if
 $d(f,v)>0$
.
$d(f,v)>0$
.
In this way one obtains a valuation on
![]() $k[x,y]$
(that may be trivial); we then get a continuous map
$k[x,y]$
(that may be trivial); we then get a continuous map
 $$\begin{eqnarray}f_{\bullet }:\{v\in V_{\infty }\mid d(f,v)>0\}\rightarrow V_{\infty }\end{eqnarray}$$
$$\begin{eqnarray}f_{\bullet }:\{v\in V_{\infty }\mid d(f,v)>0\}\rightarrow V_{\infty }\end{eqnarray}$$
defined by
 $$\begin{eqnarray}f_{\bullet }(v):=d(f,v)^{-1}f_{\ast }v.\end{eqnarray}$$
$$\begin{eqnarray}f_{\bullet }(v):=d(f,v)^{-1}f_{\ast }v.\end{eqnarray}$$
This map extends to a continuous map
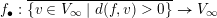 $f_{\bullet }:\overline{\{v\in V_{\infty }\mid d(f,v)>0\}}\rightarrow V_{\infty }$
. The image of any
$f_{\bullet }:\overline{\{v\in V_{\infty }\mid d(f,v)>0\}}\rightarrow V_{\infty }$
. The image of any
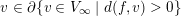 $v\in \unicode[STIX]{x2202}\{v\in V_{\infty }\mid d(f,v)>0\}$
is a curve valuation defined by a rational curve with one place at infinity.
$v\in \unicode[STIX]{x2202}\{v\in V_{\infty }\mid d(f,v)>0\}$
is a curve valuation defined by a rational curve with one place at infinity.
We now recall the following key result [Reference Favre and JonssonFJ11, Proposition 2.3, Theorem 2.4 and Proposition 5.3].
Theorem 3.3. There exists a valuation
![]() $v_{\ast }$
such that
$v_{\ast }$
such that
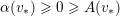 $\unicode[STIX]{x1D6FC}(v_{\ast })\geqslant 0\geqslant A(v_{\ast })$
and
$\unicode[STIX]{x1D6FC}(v_{\ast })\geqslant 0\geqslant A(v_{\ast })$
and
 $f_{\ast }v_{\ast }=\unicode[STIX]{x1D706}_{1}v_{\ast }$
.
$f_{\ast }v_{\ast }=\unicode[STIX]{x1D706}_{1}v_{\ast }$
.
If
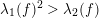 $\unicode[STIX]{x1D706}_{1}(f)^{2}>\unicode[STIX]{x1D706}_{2}(f)$
, this valuation is unique.
$\unicode[STIX]{x1D706}_{1}(f)^{2}>\unicode[STIX]{x1D706}_{2}(f)$
, this valuation is unique.
If
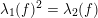 $\unicode[STIX]{x1D706}_{1}(f)^{2}=\unicode[STIX]{x1D706}_{2}(f)$
, the set of such valuations is a closed segment in
$\unicode[STIX]{x1D706}_{1}(f)^{2}=\unicode[STIX]{x1D706}_{2}(f)$
, the set of such valuations is a closed segment in
![]() $V_{\infty }$
.
$V_{\infty }$
.
This valuation
![]() $v_{\ast }$
is called the eigenvaluation of
$v_{\ast }$
is called the eigenvaluation of
![]() $f$
when
$f$
when
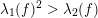 $\unicode[STIX]{x1D706}_{1}(f)^{2}>\unicode[STIX]{x1D706}_{2}(f)$
.
$\unicode[STIX]{x1D706}_{1}(f)^{2}>\unicode[STIX]{x1D706}_{2}(f)$
.
4 The Green function of
 $f$
$f$
4.1 Subharmonic functions on
 $V_{\infty }$
$V_{\infty }$
We refer to [Reference XieXie14, § 3] for details.
To any
![]() $v\in V_{\infty }$
, we attach its Green function
$v\in V_{\infty }$
, we attach its Green function
 $$\begin{eqnarray}Z_{v}(w):=\unicode[STIX]{x1D6FC}(v\wedge w).\end{eqnarray}$$
$$\begin{eqnarray}Z_{v}(w):=\unicode[STIX]{x1D6FC}(v\wedge w).\end{eqnarray}$$
This is a decreasing continuous function taking values in
![]() $[-\infty ,1]$
, satisfying
$[-\infty ,1]$
, satisfying
 $g_{v}(-\text{deg})=1$
.
$g_{v}(-\text{deg})=1$
.
Given any positive Radon measure
![]() $\unicode[STIX]{x1D70C}$
on
$\unicode[STIX]{x1D70C}$
on
![]() $V_{\infty }$
, we define
$V_{\infty }$
, we define
 $$\begin{eqnarray}Z_{\unicode[STIX]{x1D70C}}(w):=\int _{V_{\infty }}Z_{v}(w)\,d\unicode[STIX]{x1D70C}(v).\end{eqnarray}$$
$$\begin{eqnarray}Z_{\unicode[STIX]{x1D70C}}(w):=\int _{V_{\infty }}Z_{v}(w)\,d\unicode[STIX]{x1D70C}(v).\end{eqnarray}$$
Observe that
![]() $g_{v}(w)$
is always well defined as an element in
$g_{v}(w)$
is always well defined as an element in
![]() $[-\infty ,1]$
since
$[-\infty ,1]$
since
![]() $g_{v}\leqslant 1$
for all
$g_{v}\leqslant 1$
for all
![]() $v$
.
$v$
.
Then we recall the following result.
Theorem 4.1 [Reference XieXie14].
The map
![]() $\unicode[STIX]{x1D70C}\mapsto Z_{\unicode[STIX]{x1D70C}}$
is injective.
$\unicode[STIX]{x1D70C}\mapsto Z_{\unicode[STIX]{x1D70C}}$
is injective.
One can thus make the following definition.
Definition 4.2. A function
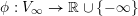 $\unicode[STIX]{x1D719}:V_{\infty }\rightarrow \mathbb{R}\cup \{-\infty \}$
is said to be subharmonic if there exists a positive Radon measure
$\unicode[STIX]{x1D719}:V_{\infty }\rightarrow \mathbb{R}\cup \{-\infty \}$
is said to be subharmonic if there exists a positive Radon measure
![]() $\unicode[STIX]{x1D70C}$
such that
$\unicode[STIX]{x1D70C}$
such that
![]() $\unicode[STIX]{x1D719}=Z_{\unicode[STIX]{x1D70C}}$
. In this case, we write
$\unicode[STIX]{x1D719}=Z_{\unicode[STIX]{x1D70C}}$
. In this case, we write
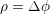 $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D719}$
and call it the Laplacian of
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D719}$
and call it the Laplacian of
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
4.2 Basic properties of the Green function of
 $f$
$f$
We refer to [Reference XieXie15a, § 12] for details.
Let
![]() $f$
be a dominant polynomial endomorphism on
$f$
be a dominant polynomial endomorphism on
![]() $\mathbb{A}_{k}^{2}$
with
$\mathbb{A}_{k}^{2}$
with
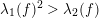 $\unicode[STIX]{x1D706}_{1}(f)^{2}>\unicode[STIX]{x1D706}_{2}(f)$
.
$\unicode[STIX]{x1D706}_{1}(f)^{2}>\unicode[STIX]{x1D706}_{2}(f)$
.
By [Reference XieXie15a, § 12], there exists a unique subharmonic function
![]() $\unicode[STIX]{x1D703}^{\ast }$
on
$\unicode[STIX]{x1D703}^{\ast }$
on
![]() $V_{\infty }$
such that:
$V_{\infty }$
such that:
-
(i)
 $f^{\ast }\unicode[STIX]{x1D703}^{\ast }=\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D703}^{\ast }$
;
$f^{\ast }\unicode[STIX]{x1D703}^{\ast }=\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D703}^{\ast }$
; -
(ii)
 $\unicode[STIX]{x1D703}^{\ast }(v)\geqslant 0$
for all
$\unicode[STIX]{x1D703}^{\ast }(v)\geqslant 0$
for all
 $v\in V_{\infty }$
;
$v\in V_{\infty }$
; -
(iii)
 $\unicode[STIX]{x1D703}^{\ast }(-\text{deg})=1$
;
$\unicode[STIX]{x1D703}^{\ast }(-\text{deg})=1$
; -
(iv) for all
 $v\in V_{\infty }$
satisfying
$v\in V_{\infty }$
satisfying
 $\unicode[STIX]{x1D6FC}(v)>-\infty$
, we have
$\unicode[STIX]{x1D6FC}(v)>-\infty$
, we have
 $\unicode[STIX]{x1D703}^{\ast }(v)>0$
if and only if
$\unicode[STIX]{x1D703}^{\ast }(v)>0$
if and only if
 $d(f^{n},v)>0$
for all
$d(f^{n},v)>0$
for all
 $n\geqslant 0$
and
$n\geqslant 0$
and  $$\begin{eqnarray}\lim _{n\rightarrow \infty }f_{\bullet }^{n}(v)=v_{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{n\rightarrow \infty }f_{\bullet }^{n}(v)=v_{\ast }.\end{eqnarray}$$
5 Metrics on projective varieties defined over a valued field
A field with an absolute value is called a valued field.
Definition 5.1. Let
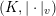 $(K,|\cdot |_{v})$
be a valued field. For any integer
$(K,|\cdot |_{v})$
be a valued field. For any integer
![]() $n\geqslant 1$
, we define a metric
$n\geqslant 1$
, we define a metric
![]() $d_{v}$
on the projective space
$d_{v}$
on the projective space
![]() $\mathbb{P}^{n}(K)$
by
$\mathbb{P}^{n}(K)$
by
 $$\begin{eqnarray}d_{v}([x_{0}:\cdots :x_{n}],[y_{0}:\cdots :y_{n}])=\frac{\max _{0\leqslant i,j\leqslant n}|x_{i}y_{j}-x_{j}y_{i}|_{v}}{\max _{0\leqslant i\leqslant n}|x_{i}|_{v}\max _{0\leqslant j\leqslant n}|y_{j}|_{v}}\end{eqnarray}$$
$$\begin{eqnarray}d_{v}([x_{0}:\cdots :x_{n}],[y_{0}:\cdots :y_{n}])=\frac{\max _{0\leqslant i,j\leqslant n}|x_{i}y_{j}-x_{j}y_{i}|_{v}}{\max _{0\leqslant i\leqslant n}|x_{i}|_{v}\max _{0\leqslant j\leqslant n}|y_{j}|_{v}}\end{eqnarray}$$
for any two points
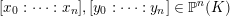 $[x_{0}:\cdots :x_{n}],[y_{0}:\cdots :y_{n}]\in \mathbb{P}^{n}(K)$
.
$[x_{0}:\cdots :x_{n}],[y_{0}:\cdots :y_{n}]\in \mathbb{P}^{n}(K)$
.
Observe that when
![]() $|\cdot |_{v}$
is Archimedean, then the metric
$|\cdot |_{v}$
is Archimedean, then the metric
![]() $d_{v}$
is not induced by a smooth Riemannian metric. However, it is equivalent to the restriction of the Fubini–Study metric on
$d_{v}$
is not induced by a smooth Riemannian metric. However, it is equivalent to the restriction of the Fubini–Study metric on
![]() $\mathbb{P}^{n}(\mathbb{C})$
or
$\mathbb{P}^{n}(\mathbb{C})$
or
![]() $\mathbb{P}^{n}(\mathbb{R})$
to
$\mathbb{P}^{n}(\mathbb{R})$
to
![]() $\mathbb{P}^{n}(K)$
induced by any embedding
$\mathbb{P}^{n}(K)$
induced by any embedding
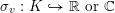 $\unicode[STIX]{x1D70E}_{v}:K{\hookrightarrow}\mathbb{R}\text{ or }\mathbb{C}$
.
$\unicode[STIX]{x1D70E}_{v}:K{\hookrightarrow}\mathbb{R}\text{ or }\mathbb{C}$
.
More generally, for a projective variety
![]() $X$
defined over
$X$
defined over
![]() $K$
, if we fix an embedding
$K$
, if we fix an embedding
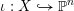 $\unicode[STIX]{x1D704}:X{\hookrightarrow}\mathbb{P}^{n}$
, we may restrict the metric
$\unicode[STIX]{x1D704}:X{\hookrightarrow}\mathbb{P}^{n}$
, we may restrict the metric
![]() $d_{v}$
on
$d_{v}$
on
![]() $\mathbb{P}^{n}(K)$
to a metric
$\mathbb{P}^{n}(K)$
to a metric
![]() $d_{v,\unicode[STIX]{x1D704}}$
on
$d_{v,\unicode[STIX]{x1D704}}$
on
![]() $X(K)$
. This metric depends on the choice of embedding
$X(K)$
. This metric depends on the choice of embedding
![]() $\unicode[STIX]{x1D704}$
in general, but, for different embeddings
$\unicode[STIX]{x1D704}$
in general, but, for different embeddings
![]() $\unicode[STIX]{x1D704}_{1}$
and
$\unicode[STIX]{x1D704}_{1}$
and
![]() $\unicode[STIX]{x1D704}_{2}$
, the metrics
$\unicode[STIX]{x1D704}_{2}$
, the metrics
![]() $d_{v,\unicode[STIX]{x1D704}_{1}}$
and
$d_{v,\unicode[STIX]{x1D704}_{1}}$
and
![]() $d_{v,\unicode[STIX]{x1D704}_{2}}$
are equivalent. Since we are mostly interested in the topology induced by these metrics, we shall usually write
$d_{v,\unicode[STIX]{x1D704}_{2}}$
are equivalent. Since we are mostly interested in the topology induced by these metrics, we shall usually write
![]() $d_{v}$
instead of
$d_{v}$
instead of
![]() $d_{v,\unicode[STIX]{x1D704}}$
for simplicity.
$d_{v,\unicode[STIX]{x1D704}}$
for simplicity.
Part II. The existence of Zariski dense orbits
The aim of this part is to prove Theorem 1.1.
6 The attracting case
In this section, we prove Theorem 1.1 in some special cases. In most of these cases, we find a Zariski dense orbit in some attracting locus. We also prove Theorem 1.1 when
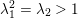 $\unicode[STIX]{x1D706}_{1}^{2}=\unicode[STIX]{x1D706}_{2}>1$
.
$\unicode[STIX]{x1D706}_{1}^{2}=\unicode[STIX]{x1D706}_{2}>1$
.
Denote by
![]() $k$
an algebraically closed field of characteristic
$k$
an algebraically closed field of characteristic
![]() $0$
. Let
$0$
. Let
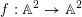 $f:\mathbb{A}^{2}\rightarrow \mathbb{A}^{2}$
be a dominant polynomial endomorphism defined over
$f:\mathbb{A}^{2}\rightarrow \mathbb{A}^{2}$
be a dominant polynomial endomorphism defined over
![]() $k$
. We have the following result.
$k$
. We have the following result.
Lemma 6.1. If
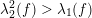 $\unicode[STIX]{x1D706}_{2}^{2}(f)>\unicode[STIX]{x1D706}_{1}(f)$
and the eigenvaluation
$\unicode[STIX]{x1D706}_{2}^{2}(f)>\unicode[STIX]{x1D706}_{1}(f)$
and the eigenvaluation
![]() $v_{\ast }$
is not divisorial, then there exists a point
$v_{\ast }$
is not divisorial, then there exists a point
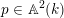 $p\in \mathbb{A}^{2}(k)$
whose orbit is Zariski dense in
$p\in \mathbb{A}^{2}(k)$
whose orbit is Zariski dense in
![]() $\mathbb{A}^{2}$
.
$\mathbb{A}^{2}$
.
Proof of Lemma 6.1.
After replacing
![]() $k$
by an algebraically closed subfield of
$k$
by an algebraically closed subfield of
![]() $k$
containing all the coefficients of
$k$
containing all the coefficients of
![]() $f$
, we may suppose that the transcendence degree of
$f$
, we may suppose that the transcendence degree of
![]() $k$
over
$k$
over
![]() $\bar{\mathbb{Q}}$
is finite.
$\bar{\mathbb{Q}}$
is finite.
By [Reference Favre and JonssonFJ11, Theorem 3.1], there exist a compactification
![]() $X$
of
$X$
of
![]() $\mathbb{A}^{2}$
defined over
$\mathbb{A}^{2}$
defined over
![]() $k$
and a superattracting point
$k$
and a superattracting point
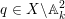 $q\in X\setminus \mathbb{A}_{k}^{2}$
such that for any valuation
$q\in X\setminus \mathbb{A}_{k}^{2}$
such that for any valuation
![]() $v\in V_{\infty }$
whose center in
$v\in V_{\infty }$
whose center in
![]() $X$
is
$X$
is
![]() $q$
, we have
$q$
, we have
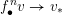 $f_{\bullet }^{n}v\rightarrow v_{\ast }$
as
$f_{\bullet }^{n}v\rightarrow v_{\ast }$
as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
By embedding
![]() $k$
in
$k$
in
![]() $\mathbb{C}$
, we endow
$\mathbb{C}$
, we endow
![]() $X$
with the usual Euclidean topology. There exists a neighborhood
$X$
with the usual Euclidean topology. There exists a neighborhood
![]() $U$
of
$U$
of
![]() $q$
in
$q$
in
![]() $X$
such that:
$X$
such that:
-
(i)
 $I(f)\cap U=\emptyset$
;
$I(f)\cap U=\emptyset$
; -
(ii)
 $f(U)\subseteq U$
;
$f(U)\subseteq U$
; -
(iii) for any point
 $p\in U$
,
$p\in U$
,
 $f^{n}(p)\rightarrow q$
as
$f^{n}(p)\rightarrow q$
as
 $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
Since
![]() $\mathbb{A}^{2}(k)$
is dense in
$\mathbb{A}^{2}(k)$
is dense in
![]() $\mathbb{A}^{2}(\mathbb{C})$
, there exists a point
$\mathbb{A}^{2}(\mathbb{C})$
, there exists a point
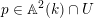 $p\in \mathbb{A}^{2}(k)\cap U$
. If the orbit of
$p\in \mathbb{A}^{2}(k)\cap U$
. If the orbit of
![]() $p$
is not Zariski dense, then its Zariski closure
$p$
is not Zariski dense, then its Zariski closure
![]() $Z$
is a union of finitely many curves. Since
$Z$
is a union of finitely many curves. Since
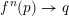 $f^{n}(p)\rightarrow q$
,
$f^{n}(p)\rightarrow q$
,
![]() $p$
is not preperiodic. It follows that all the one-dimensional irreducible components of
$p$
is not preperiodic. It follows that all the one-dimensional irreducible components of
![]() $Z$
are periodic under
$Z$
are periodic under
![]() $f$
. Let
$f$
. Let
![]() $C$
be a one-dimensional irreducible component of
$C$
be a one-dimensional irreducible component of
![]() $Z$
. Since there exists an infinite sequence
$Z$
. Since there exists an infinite sequence
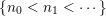 $\{n_{0}<n_{1}<\cdots \,\}$
such that
$\{n_{0}<n_{1}<\cdots \,\}$
such that
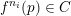 $f^{n_{i}}(p)\in C$
for
$f^{n_{i}}(p)\in C$
for
![]() $i\geqslant 0$
, we have that
$i\geqslant 0$
, we have that
![]() $C$
contains
$C$
contains
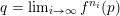 $q=\lim _{i\rightarrow \infty }f^{n_{i}}(p)$
. Then there exists a branch
$q=\lim _{i\rightarrow \infty }f^{n_{i}}(p)$
. Then there exists a branch
![]() $C_{1}$
of
$C_{1}$
of
![]() $C$
at infinity satisfying
$C$
at infinity satisfying
![]() $q\in C_{1}$
. Thus,
$q\in C_{1}$
. Thus,
![]() $v_{C_{1}}$
is periodic, which is a contradiction. It follows that
$v_{C_{1}}$
is periodic, which is a contradiction. It follows that
![]() $O(p)$
is Zariski dense.◻
$O(p)$
is Zariski dense.◻
In many cases, for example
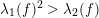 $\unicode[STIX]{x1D706}_{1}(f)^{2}>\unicode[STIX]{x1D706}_{2}(f)$
and
$\unicode[STIX]{x1D706}_{1}(f)^{2}>\unicode[STIX]{x1D706}_{2}(f)$
and
![]() $v_{\ast }$
is divisorial, there exist a projective compactification
$v_{\ast }$
is divisorial, there exist a projective compactification
![]() $X$
of
$X$
of
![]() $\mathbb{A}^{2}$
and an irreducible component
$\mathbb{A}^{2}$
and an irreducible component
![]() $E$
of
$E$
of
![]() $X\setminus \mathbb{A}^{2}$
satisfying
$X\setminus \mathbb{A}^{2}$
satisfying
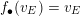 $f_{\bullet }(v_{E})=v_{E}$
. The following result proves Theorem 1.1 when
$f_{\bullet }(v_{E})=v_{E}$
. The following result proves Theorem 1.1 when
![]() $f|_{E}$
is of infinite order.
$f|_{E}$
is of infinite order.
Lemma 6.2. Let
![]() $X$
be a projective compactification of
$X$
be a projective compactification of
![]() $\mathbb{A}^{2}$
defined over
$\mathbb{A}^{2}$
defined over
![]() $k$
. Then
$k$
. Then
![]() $f$
extends to a rational selfmap on
$f$
extends to a rational selfmap on
![]() $X$
. Let
$X$
. Let
![]() $E$
be an irreducible component of
$E$
be an irreducible component of
![]() $X\setminus \mathbb{A}^{2}$
satisfying
$X\setminus \mathbb{A}^{2}$
satisfying
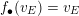 $f_{\bullet }(v_{E})=v_{E}$
,
$f_{\bullet }(v_{E})=v_{E}$
,
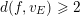 $d(f,v_{E})\geqslant 2$
and
$d(f,v_{E})\geqslant 2$
and
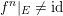 $f^{n}|_{E}\neq \operatorname{id}$
for all
$f^{n}|_{E}\neq \operatorname{id}$
for all
![]() $n\geqslant 1$
. Then there exists a point
$n\geqslant 1$
. Then there exists a point
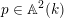 $p\in \mathbb{A}^{2}(k)$
whose orbit is Zariski dense in
$p\in \mathbb{A}^{2}(k)$
whose orbit is Zariski dense in
![]() $\mathbb{A}^{2}$
.
$\mathbb{A}^{2}$
.
Proof of Lemma 6.2.
There exists a finitely generated
![]() $\mathbb{Z}$
-subalgebra
$\mathbb{Z}$
-subalgebra
![]() $R$
of
$R$
of
![]() $k$
such that
$k$
such that
![]() $X$
,
$X$
,
![]() $E$
and
$E$
and
![]() $f$
are defined over the fraction field
$f$
are defined over the fraction field
![]() $K$
of
$K$
of
![]() $R$
.
$R$
.
By [Reference BellBel06, Lemma 3.1], there exist a prime
![]() $\mathfrak{p}\geqslant 3$
, an embedding of
$\mathfrak{p}\geqslant 3$
, an embedding of
![]() $K$
into
$K$
into
![]() $\mathbb{Q}_{\mathfrak{p}}$
and a
$\mathbb{Q}_{\mathfrak{p}}$
and a
![]() $\mathbb{Z}_{\mathfrak{p}}$
-scheme
$\mathbb{Z}_{\mathfrak{p}}$
-scheme
![]() ${\mathcal{X}}_{Z_{\mathfrak{p}}}$
such that the generic fiber is
${\mathcal{X}}_{Z_{\mathfrak{p}}}$
such that the generic fiber is
![]() $X$
, the specialization
$X$
, the specialization
![]() $E_{\mathfrak{p}}$
of
$E_{\mathfrak{p}}$
of
![]() $E$
is isomorphic to
$E$
is isomorphic to
![]() $\mathbb{P}_{\mathbb{F}_{\mathfrak{p}}}^{1}$
, the specialization
$\mathbb{P}_{\mathbb{F}_{\mathfrak{p}}}^{1}$
, the specialization
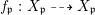 $f_{\mathfrak{p}}:X_{\mathfrak{p}}{\dashrightarrow}X_{\mathfrak{p}}$
of
$f_{\mathfrak{p}}:X_{\mathfrak{p}}{\dashrightarrow}X_{\mathfrak{p}}$
of
![]() $f$
at the prime ideal
$f$
at the prime ideal
![]() $\mathfrak{p}$
of
$\mathfrak{p}$
of
![]() $Z_{\mathfrak{p}}$
is dominant and
$Z_{\mathfrak{p}}$
is dominant and
 $\operatorname{deg}f_{\mathfrak{p}}|_{E_{\mathfrak{p}}}=\operatorname{deg}f_{E}$
.
$\operatorname{deg}f_{\mathfrak{p}}|_{E_{\mathfrak{p}}}=\operatorname{deg}f_{E}$
.
Since there are only finitely many points in the orbits of
![]() $I(f_{\mathfrak{p}})$
and the orbits of ramified points of
$I(f_{\mathfrak{p}})$
and the orbits of ramified points of
![]() $f_{\mathfrak{p}}$
, by [Reference FakhruddinFak03, Proposition 5.5], there exists a closed point
$f_{\mathfrak{p}}$
, by [Reference FakhruddinFak03, Proposition 5.5], there exists a closed point
![]() $x\in E_{\mathfrak{p}}$
such that
$x\in E_{\mathfrak{p}}$
such that
![]() $x$
is periodic,
$x$
is periodic,
![]() $E_{\mathfrak{p}}$
is the unique irreducible component of
$E_{\mathfrak{p}}$
is the unique irreducible component of
![]() $X_{\mathfrak{p}}\setminus \mathbb{A}_{\mathfrak{p}}^{2}$
containing
$X_{\mathfrak{p}}\setminus \mathbb{A}_{\mathfrak{p}}^{2}$
containing
![]() $x$
,
$x$
,
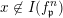 $x\not \in I(f_{\mathfrak{p}}^{n})$
for all
$x\not \in I(f_{\mathfrak{p}}^{n})$
for all
![]() $n\geqslant 0$
and
$n\geqslant 0$
and
![]() $f_{\mathfrak{p}}|_{E_{\mathfrak{p}}}$
is not ramified at any point on the orbit of
$f_{\mathfrak{p}}|_{E_{\mathfrak{p}}}$
is not ramified at any point on the orbit of
![]() $x$
. After replacing
$x$
. After replacing
![]() $\mathbb{Q}_{\mathfrak{p}}$
by a finite extension
$\mathbb{Q}_{\mathfrak{p}}$
by a finite extension
![]() $K_{\mathfrak{p}}$
, we may suppose that
$K_{\mathfrak{p}}$
, we may suppose that
![]() $x$
is defined over
$x$
is defined over
![]() $O_{K_{\mathfrak{p}}}/\mathfrak{p}$
. After replacing
$O_{K_{\mathfrak{p}}}/\mathfrak{p}$
. After replacing
![]() $f$
by a positive iterate, we may suppose that
$f$
by a positive iterate, we may suppose that
![]() $x$
is fixed by
$x$
is fixed by
![]() $f_{\mathfrak{p}}$
.
$f_{\mathfrak{p}}$
.
The fixed point
![]() $x$
of
$x$
of
![]() $f_{\mathfrak{p}}$
defines an open and closed polydisc
$f_{\mathfrak{p}}$
defines an open and closed polydisc
![]() $U$
in
$U$
in
![]() $X(K_{\mathfrak{p}})$
with respect to the
$X(K_{\mathfrak{p}})$
with respect to the
![]() $\mathfrak{p}$
-adic norm
$\mathfrak{p}$
-adic norm
![]() $|\cdot |_{\mathfrak{p}}$
. We have
$|\cdot |_{\mathfrak{p}}$
. We have
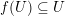 $f(U)\subseteq U$
. Observe that
$f(U)\subseteq U$
. Observe that
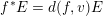 $f^{\ast }E=d(f,v)E$
in
$f^{\ast }E=d(f,v)E$
in
![]() $U$
and
$U$
and
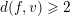 $d(f,v)\geqslant 2$
. So, for all points
$d(f,v)\geqslant 2$
. So, for all points
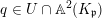 $q\in U\cap \mathbb{A}^{2}(K_{\mathfrak{p}})$
, we have
$q\in U\cap \mathbb{A}^{2}(K_{\mathfrak{p}})$
, we have
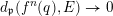 $d_{\mathfrak{p}}(f^{n}(q),E)\rightarrow 0$
as
$d_{\mathfrak{p}}(f^{n}(q),E)\rightarrow 0$
as
![]() $n\rightarrow \infty$
.
$n\rightarrow \infty$
.
Since
![]() $f_{\mathfrak{p}}|_{E_{\mathfrak{p}}}$
is not ramified at
$f_{\mathfrak{p}}|_{E_{\mathfrak{p}}}$
is not ramified at
![]() $x$
, after replacing
$x$
, after replacing
![]() $f$
by some positive iterate, we may suppose that
$f$
by some positive iterate, we may suppose that
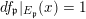 $df_{\mathfrak{p}}|_{E_{\mathfrak{p}}}(x)=1$
. By [Reference PoonenPoo14, Theorem 1], we have that for any point
$df_{\mathfrak{p}}|_{E_{\mathfrak{p}}}(x)=1$
. By [Reference PoonenPoo14, Theorem 1], we have that for any point
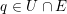 $q\in U\cap E$
, there exists a
$q\in U\cap E$
, there exists a
![]() $\mathfrak{p}$
-adic analytic map
$\mathfrak{p}$
-adic analytic map
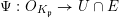 $\unicode[STIX]{x1D6F9}:O_{K_{\mathfrak{p}}}\rightarrow U\cap E$
such that for any
$\unicode[STIX]{x1D6F9}:O_{K_{\mathfrak{p}}}\rightarrow U\cap E$
such that for any
![]() $n\geqslant 0$
, we have
$n\geqslant 0$
, we have
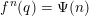 $f^{n}(q)=\unicode[STIX]{x1D6F9}(n)$
.
$f^{n}(q)=\unicode[STIX]{x1D6F9}(n)$
.
If there exists a preperiodic point
![]() $q$
in
$q$
in
![]() $U\cap E$
, then there exists
$U\cap E$
, then there exists
![]() $m\geqslant 0$
such that
$m\geqslant 0$
such that
![]() $f^{m}(q)$
is periodic. Then there are infinitely many
$f^{m}(q)$
is periodic. Then there are infinitely many
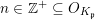 $n\in \mathbb{Z}^{+}\subseteq O_{K_{\mathfrak{p}}}$
such that
$n\in \mathbb{Z}^{+}\subseteq O_{K_{\mathfrak{p}}}$
such that
 $\unicode[STIX]{x1D6F9}(n)=f^{m}(q)$
. The fact that
$\unicode[STIX]{x1D6F9}(n)=f^{m}(q)$
. The fact that
![]() $O_{K_{\mathfrak{p}}}$
is compact shows that
$O_{K_{\mathfrak{p}}}$
is compact shows that
![]() $\unicode[STIX]{x1D6F9}$
is constant. It follows that
$\unicode[STIX]{x1D6F9}$
is constant. It follows that
![]() $q$
is fixed. Thus, all preperiodic points in
$q$
is fixed. Thus, all preperiodic points in
![]() $U\cap E$
are fixed by
$U\cap E$
are fixed by
![]() $f|_{E}$
.
$f|_{E}$
.
Let
![]() $S$
be the set of all fixed points in
$S$
be the set of all fixed points in
![]() $U\cap E$
. Since
$U\cap E$
. Since
 $f^{n}|_{E}\neq \operatorname{id}$
for all
$f^{n}|_{E}\neq \operatorname{id}$
for all
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
![]() $S$
is finite.
$S$
is finite.
We first treat the case
![]() $S=\emptyset$
. Pick a point
$S=\emptyset$
. Pick a point
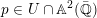 $p\in U\cap \mathbb{A}^{2}(\bar{\mathbb{Q}})$
. Then
$p\in U\cap \mathbb{A}^{2}(\bar{\mathbb{Q}})$
. Then
![]() $p$
is not preperiodic. If
$p$
is not preperiodic. If
![]() $O(p)$
is not Zariski dense, we denote by
$O(p)$
is not Zariski dense, we denote by
![]() $Z$
its Zariski closure. Pick a one-dimensional irreducible component
$Z$
its Zariski closure. Pick a one-dimensional irreducible component
![]() $C$
of
$C$
of
![]() $Z$
. We have
$Z$
. We have
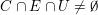 $C\cap E\cap U\neq \emptyset$
and, for all points
$C\cap E\cap U\neq \emptyset$
and, for all points
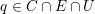 $q\in C\cap E\cap U$
,
$q\in C\cap E\cap U$
,
![]() $q$
is preperiodic under
$q$
is preperiodic under
![]() $f|_{E}$
. This contradicts our assumption, so
$f|_{E}$
. This contradicts our assumption, so
![]() $O(p)$
is Zariski dense.
$O(p)$
is Zariski dense.
Next, we treat the case
![]() $S\neq \emptyset$
. Since
$S\neq \emptyset$
. Since
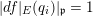 $|df|_{E}(q_{i})|_{\mathfrak{p}}=1$
for all
$|df|_{E}(q_{i})|_{\mathfrak{p}}=1$
for all
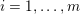 $i=1,\ldots ,m$
, we have
$i=1,\ldots ,m$
, we have
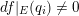 $df|_{E}(q_{i})\neq 0$
. By embedding
$df|_{E}(q_{i})\neq 0$
. By embedding
![]() $K$
in
$K$
in
![]() $\mathbb{C}$
, we endow
$\mathbb{C}$
, we endow
![]() $X$
with the usual Euclidean topology. By [Reference AbateAba01, Theorem 3.1.4], for any
$X$
with the usual Euclidean topology. By [Reference AbateAba01, Theorem 3.1.4], for any
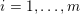 $i=1,\ldots ,m$
, there exists a unique complex analytic manifold
$i=1,\ldots ,m$
, there exists a unique complex analytic manifold
![]() $W$
not contained in
$W$
not contained in
![]() $E$
such that
$E$
such that
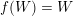 $f(W)=W$
. It follows that there are at most one irreducible algebraic curve
$f(W)=W$
. It follows that there are at most one irreducible algebraic curve
![]() $C_{i}\neq E$
in
$C_{i}\neq E$
in
![]() $X$
such that
$X$
such that
![]() $q_{i}\in C_{i}$
and
$q_{i}\in C_{i}$
and
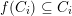 $f(C_{i})\subseteq C_{i}$
. For convenience, if such an algebraic curve does not exist, we define
$f(C_{i})\subseteq C_{i}$
. For convenience, if such an algebraic curve does not exist, we define
![]() $C_{i}$
to be
$C_{i}$
to be
![]() $\emptyset$
.
$\emptyset$
.
For any
![]() $n\geqslant 1$
, by applying [Reference AbateAba01, Theorem 3.1.4] for
$n\geqslant 1$
, by applying [Reference AbateAba01, Theorem 3.1.4] for
![]() $f^{n}$
, if
$f^{n}$
, if
![]() $C$
is a curve satisfying
$C$
is a curve satisfying
![]() $q_{i}\in C$
and
$q_{i}\in C$
and
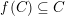 $f(C)\subseteq C$
, then
$f(C)\subseteq C$
, then
![]() $C=C_{i}$
. Moreover if
$C=C_{i}$
. Moreover if
![]() $C^{\prime }$
is an irreducible component of
$C^{\prime }$
is an irreducible component of
 $f^{-1}(C_{i})$
such that
$f^{-1}(C_{i})$
such that
![]() $q\in C^{\prime }$
, then, for any point
$q\in C^{\prime }$
, then, for any point
![]() $y\in C^{\prime }$
near
$y\in C^{\prime }$
near
![]() $q$
with respect to the Euclidean topology, we have
$q$
with respect to the Euclidean topology, we have
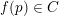 $f(p)\in C$
. Then, by [Reference AbateAba01, (iv) of Theorem 3.1.4], we have
$f(p)\in C$
. Then, by [Reference AbateAba01, (iv) of Theorem 3.1.4], we have
![]() $p\in C$
. It follows that
$p\in C$
. It follows that
![]() $C^{\prime }=C$
. Thus, there exists a small open and closed neighborhood
$C^{\prime }=C$
. Thus, there exists a small open and closed neighborhood
![]() $U_{i}$
of
$U_{i}$
of
![]() $q_{i}$
with respect to the norm
$q_{i}$
with respect to the norm
![]() $|\cdot |_{\mathfrak{p}}$
such that for all
$|\cdot |_{\mathfrak{p}}$
such that for all
![]() $j\neq i$
,
$j\neq i$
,
![]() $q_{j}\not \in U_{i}$
,
$q_{j}\not \in U_{i}$
,
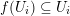 $f(U_{i})\subseteq U_{i}$
and
$f(U_{i})\subseteq U_{i}$
and
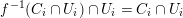 $f^{-1}(C_{i}\cap U_{i})\cap U_{i}=C_{i}\cap U_{i}$
.
$f^{-1}(C_{i}\cap U_{i})\cap U_{i}=C_{i}\cap U_{i}$
.
Observe that
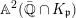 $\mathbb{A}^{2}(\bar{\mathbb{Q}}\cap K_{\mathfrak{p}})$
is dense in
$\mathbb{A}^{2}(\bar{\mathbb{Q}}\cap K_{\mathfrak{p}})$
is dense in
![]() $\mathbb{A}^{2}(K_{\mathfrak{p}})$
with respect to
$\mathbb{A}^{2}(K_{\mathfrak{p}})$
with respect to
![]() $|\cdot |_{\mathfrak{p}}$
.
$|\cdot |_{\mathfrak{p}}$
.
There exists a
![]() $\bar{\mathbb{Q}}$
-point
$\bar{\mathbb{Q}}$
-point
![]() $p$
in
$p$
in
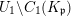 $U_{1}\setminus C_{1}(K_{\mathfrak{p}})$
. If the orbit
$U_{1}\setminus C_{1}(K_{\mathfrak{p}})$
. If the orbit
![]() $O(p)$
of
$O(p)$
of
![]() $p$
is not Zariski dense, denote by
$p$
is not Zariski dense, denote by
![]() $Z$
its Zariski closure. Since
$Z$
its Zariski closure. Since
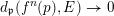 $d_{\mathfrak{p}}(f^{n}(p),E)\rightarrow 0$
as
$d_{\mathfrak{p}}(f^{n}(p),E)\rightarrow 0$
as
![]() $n\rightarrow \infty$
,
$n\rightarrow \infty$
,
![]() $p$
is not preperiodic. It follows that there exists a one-dimensional irreducible component
$p$
is not preperiodic. It follows that there exists a one-dimensional irreducible component
![]() $C$
of
$C$
of
![]() $Z$
which is periodic. There exist
$Z$
which is periodic. There exist
![]() $a,b>0$
such that
$a,b>0$
such that
 $f^{an+b}(p)\in C$
for all
$f^{an+b}(p)\in C$
for all
![]() $n\geqslant 0$
. Since
$n\geqslant 0$
. Since
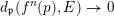 $d_{\mathfrak{p}}(f^{n}(p),E)\rightarrow 0$
as
$d_{\mathfrak{p}}(f^{n}(p),E)\rightarrow 0$
as
![]() $n\rightarrow \infty$
and
$n\rightarrow \infty$
and
![]() $U_{1}$
is closed, there exists a point
$U_{1}$
is closed, there exists a point
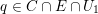 $q\in C\cap E\cap U_{1}$
. It follows that
$q\in C\cap E\cap U_{1}$
. It follows that
![]() $q$
is periodic under
$q$
is periodic under
![]() $f|_{E}$
. Then
$f|_{E}$
. Then
![]() $q$
is fixed and
$q$
is fixed and
![]() $q=q_{1}$
. This implies that
$q=q_{1}$
. This implies that
![]() $C=C_{1}$
. Since
$C=C_{1}$
. Since
 $f^{b}(p)\in C_{1}\cap V$
and
$f^{b}(p)\in C_{1}\cap V$
and
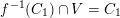 $f^{-1}(C_{1})\cap V=C_{1}$
, we have
$f^{-1}(C_{1})\cap V=C_{1}$
, we have
![]() $p\in C_{1}$
, which is a contradiction. It follows that
$p\in C_{1}$
, which is a contradiction. It follows that
![]() $O(p)$
is Zariski dense.◻
$O(p)$
is Zariski dense.◻
Proposition 6.3. If
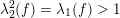 $\unicode[STIX]{x1D706}_{2}^{2}(f)=\unicode[STIX]{x1D706}_{1}(f)>1$
, then Theorem 1.1 holds.
$\unicode[STIX]{x1D706}_{2}^{2}(f)=\unicode[STIX]{x1D706}_{1}(f)>1$
, then Theorem 1.1 holds.
Proof of Proposition 6.3.
By [Reference Favre and JonssonFJ11, Proposition 5.1] and [Reference Favre and JonssonFJ11, Proposition 5.3], there exists a divisorial valuation
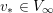 $v_{\ast }\in V_{\infty }$
satisfying
$v_{\ast }\in V_{\infty }$
satisfying
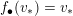 $f_{\bullet }(v_{\ast })=v_{\ast }$
and
$f_{\bullet }(v_{\ast })=v_{\ast }$
and
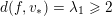 $d(f,v_{\ast })=\unicode[STIX]{x1D706}_{1}\geqslant 2$
. Moreover, there exist a compactification
$d(f,v_{\ast })=\unicode[STIX]{x1D706}_{1}\geqslant 2$
. Moreover, there exist a compactification
![]() $X$
of
$X$
of
![]() $\mathbb{A}^{2}$
and an irreducible component
$\mathbb{A}^{2}$
and an irreducible component
![]() $E$
in
$E$
in
![]() $X\setminus \mathbb{A}^{2}$
satisfying
$X\setminus \mathbb{A}^{2}$
satisfying
 $v_{\ast }=v_{E}$
and
$v_{\ast }=v_{E}$
and
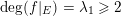 $\operatorname{deg}(f|_{E})=\unicode[STIX]{x1D706}_{1}\geqslant 2$
. We conclude our theorem by invoking Lemma 6.2.◻
$\operatorname{deg}(f|_{E})=\unicode[STIX]{x1D706}_{1}\geqslant 2$
. We conclude our theorem by invoking Lemma 6.2.◻
7 Totally invariant curves
Let
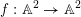 $f:\mathbb{A}^{2}\rightarrow \mathbb{A}^{2}$
be a dominant polynomial endomorphism defined over an algebraically closed field
$f:\mathbb{A}^{2}\rightarrow \mathbb{A}^{2}$
be a dominant polynomial endomorphism defined over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $0$
. Let
$0$
. Let
![]() $X$
be a compactification of
$X$
be a compactification of
![]() $\mathbb{A}_{k}^{2}$
. Then
$\mathbb{A}_{k}^{2}$
. Then
![]() $f$
extends to a rational selfmap on
$f$
extends to a rational selfmap on
![]() $X$
.
$X$
.
As in [Reference CantatCan10], a curve
![]() $C$
in
$C$
in
![]() $X$
is said to be
$X$
is said to be
![]() $totally$
$totally$
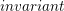 $invariant$
if the strict transform
$invariant$
if the strict transform
![]() $f^{\#}C$
equals
$f^{\#}C$
equals
![]() $C$
.
$C$
.
If there are infinitely many irreducible totally invariant curves in
![]() $\mathbb{A}_{k}^{2}$
, then [Reference CantatCan10, Theorem B] shows that
$\mathbb{A}_{k}^{2}$
, then [Reference CantatCan10, Theorem B] shows that
![]() $f$
preserves a nontrivial fibration.
$f$
preserves a nontrivial fibration.
Proposition 7.1. If there are infinitely many irreducible curves in
![]() $\mathbb{A}_{k}^{2}$
that are totally invariant under
$\mathbb{A}_{k}^{2}$
that are totally invariant under
![]() $f$
, then there is a nonconstant rational function
$f$
, then there is a nonconstant rational function
![]() $g$
satisfying
$g$
satisfying
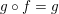 $g\circ f=g$
.
$g\circ f=g$
.
In this section, we give a direct proof of this result.
Proof of Proposition 7.1.
Let
![]() $\{C_{i}\}_{i\geqslant 1}$
be an infinite sequence of distinct irreducible totally invariant curves in
$\{C_{i}\}_{i\geqslant 1}$
be an infinite sequence of distinct irreducible totally invariant curves in
![]() $\mathbb{A}_{k}^{2}$
. Since the ramification locus of
$\mathbb{A}_{k}^{2}$
. Since the ramification locus of
![]() $f$
is of dimension at most
$f$
is of dimension at most
![]() $1$
, after replacing
$1$
, after replacing
![]() $\{C_{i}\}_{i\geqslant 1}$
by an infinite subsequence, we may suppose that
$\{C_{i}\}_{i\geqslant 1}$
by an infinite subsequence, we may suppose that
![]() $C_{i}$
is not contained in the ramification locus of
$C_{i}$
is not contained in the ramification locus of
![]() $f$
for any
$f$
for any
![]() $i\geqslant 0$
. Then we have
$i\geqslant 0$
. Then we have
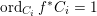 $\operatorname{ord}_{C_{i}}f^{\ast }C_{i}=1$
for all
$\operatorname{ord}_{C_{i}}f^{\ast }C_{i}=1$
for all
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
Let
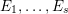 $E_{1},\ldots ,E_{s}$
be the set of irreducible curves in
$E_{1},\ldots ,E_{s}$
be the set of irreducible curves in
![]() $\mathbb{A}^{2}$
contracted by
$\mathbb{A}^{2}$
contracted by
![]() $f$
. Let
$f$
. Let
![]() $V$
be the
$V$
be the
![]() $\mathbb{Q}$
-subspace in
$\mathbb{Q}$
-subspace in
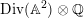 $\operatorname{Div}(\mathbb{A}^{2})\otimes \mathbb{Q}$
spanned by
$\operatorname{Div}(\mathbb{A}^{2})\otimes \mathbb{Q}$
spanned by
![]() $E_{i}$
,
$E_{i}$
,
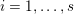 $i=1,\ldots ,s$
. Then we have
$i=1,\ldots ,s$
. Then we have
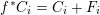 $f^{\ast }C_{i}=C_{i}+F_{i}$
, where
$f^{\ast }C_{i}=C_{i}+F_{i}$
, where
![]() $F_{i}\in V$
for all
$F_{i}\in V$
for all
![]() $i\geqslant 1$
. Set
$i\geqslant 1$
. Set
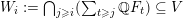 $W_{i}:=\bigcap _{j\geqslant i}(\sum _{t\geqslant j}\mathbb{Q}F_{t})\subseteq V$
. We have
$W_{i}:=\bigcap _{j\geqslant i}(\sum _{t\geqslant j}\mathbb{Q}F_{t})\subseteq V$
. We have
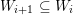 $W_{i+1}\subseteq W_{i}$
for
$W_{i+1}\subseteq W_{i}$
for
![]() $i\geqslant 1$
. Since
$i\geqslant 1$
. Since
![]() $V$
is of finite dimension, there exists
$V$
is of finite dimension, there exists
![]() $n_{0}\geqslant 1$
such that
$n_{0}\geqslant 1$
such that
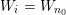 $W_{i}=W_{n_{0}}$
for all
$W_{i}=W_{n_{0}}$
for all
![]() $i\geqslant n_{0}$
. We may suppose that
$i\geqslant n_{0}$
. We may suppose that
![]() $n_{0}=1$
and set
$n_{0}=1$
and set
 $W:=W_{n_{0}}$
. Moreover, we may suppose that
$W:=W_{n_{0}}$
. Moreover, we may suppose that
![]() $W$
is generated by
$W$
is generated by
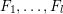 $F_{1},\ldots ,F_{l}$
, where
$F_{1},\ldots ,F_{l}$
, where
 $l=\dim W$
.
$l=\dim W$
.
For all
 $i\geqslant l+1$
, we have
$i\geqslant l+1$
, we have
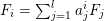 $F_{i}=\sum _{j=1}^{l}a_{j}^{i}F_{j}$
, where
$F_{i}=\sum _{j=1}^{l}a_{j}^{i}F_{j}$
, where
![]() $a_{j}^{i}\in \mathbb{Q}$
. Since
$a_{j}^{i}\in \mathbb{Q}$
. Since
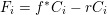 $F_{i}=f^{\ast }C_{i}-rC_{i}$
, we have
$F_{i}=f^{\ast }C_{i}-rC_{i}$
, we have
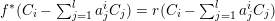 $f^{\ast }(C_{i}-\sum _{j=1}^{l}a_{j}^{i}C_{j})=r(C_{i}-\sum _{j=1}^{l}a_{j}^{i}C_{j})$
. There exists
$f^{\ast }(C_{i}-\sum _{j=1}^{l}a_{j}^{i}C_{j})=r(C_{i}-\sum _{j=1}^{l}a_{j}^{i}C_{j})$
. There exists
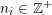 $n_{i}\in \mathbb{Z}^{+}$
such that
$n_{i}\in \mathbb{Z}^{+}$
such that
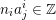 $n_{i}a_{j}^{i}\in \mathbb{Z}$
for all
$n_{i}a_{j}^{i}\in \mathbb{Z}$
for all
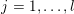 $j=1,\ldots ,l$
. Then we have
$j=1,\ldots ,l$
. Then we have
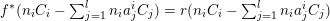 $f^{\ast }(n_{i}C_{i}-\sum _{j=1}^{l}n_{i}a_{j}^{i}C_{j})=r(n_{i}C_{i}-\sum _{j=1}^{l}n_{i}a_{j}^{i}C_{j})$
. Up to multiplication by a nonzero constant, there exists a unique
$f^{\ast }(n_{i}C_{i}-\sum _{j=1}^{l}n_{i}a_{j}^{i}C_{j})=r(n_{i}C_{i}-\sum _{j=1}^{l}n_{i}a_{j}^{i}C_{j})$
. Up to multiplication by a nonzero constant, there exists a unique
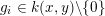 $g_{i}\in k(x,y)\setminus \{0\}$
such that
$g_{i}\in k(x,y)\setminus \{0\}$
such that
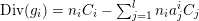 $\operatorname{Div}(g_{i})=n_{i}C_{i}-\sum _{j=1}^{l}n_{i}a_{j}^{i}C_{j}$
. It follows that
$\operatorname{Div}(g_{i})=n_{i}C_{i}-\sum _{j=1}^{l}n_{i}a_{j}^{i}C_{j}$
. It follows that
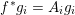 $f^{\ast }g_{i}=A_{i}g_{i}$
, where
$f^{\ast }g_{i}=A_{i}g_{i}$
, where
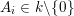 $A_{i}\in k\setminus \{0\}$
. Since
$A_{i}\in k\setminus \{0\}$
. Since
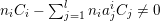 $n_{i}C_{i}-\sum _{j=1}^{l}n_{i}a_{j}^{i}C_{j}\neq 0$
for
$n_{i}C_{i}-\sum _{j=1}^{l}n_{i}a_{j}^{i}C_{j}\neq 0$
for
 $i\geqslant l+1$
,
$i\geqslant l+1$
,
![]() $g_{i}$
is nonconstant for
$g_{i}$
is nonconstant for
 $i\geqslant l+1$
. This concludes the proof.◻
$i\geqslant l+1$
. This concludes the proof.◻
Corollary 7.2. If
![]() $f$
is birational, then either there is a nonconstant rational function
$f$
is birational, then either there is a nonconstant rational function
![]() $g$
satisfying
$g$
satisfying
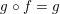 $g\circ f=g$
, or there exists a point
$g\circ f=g$
, or there exists a point
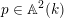 $p\in \mathbb{A}^{2}(k)$
with Zariski dense orbit.
$p\in \mathbb{A}^{2}(k)$
with Zariski dense orbit.
Proof of Corollary 7.2.
There exists a finite generated
![]() $\mathbb{Q}$
-subalgebra
$\mathbb{Q}$
-subalgebra
![]() $R$
of
$R$
of
![]() $k$
such that
$k$
such that
![]() $f$
is defined over
$f$
is defined over
![]() $R$
. Denote by
$R$
. Denote by
![]() $K$
the fraction field of
$K$
the fraction field of
![]() $R$
.
$R$
.
By [Reference BellBel06, Lemma 3.1], there exist a prime
![]() $\mathfrak{p}\geqslant 3$
and an embedding of
$\mathfrak{p}\geqslant 3$
and an embedding of
![]() $R$
into
$R$
into
![]() $\mathbb{Z}_{\mathfrak{p}}$
such that all coefficients of
$\mathbb{Z}_{\mathfrak{p}}$
such that all coefficients of
![]() $f$
are of
$f$
are of
![]() $\mathfrak{p}$
-adic norm
$\mathfrak{p}$
-adic norm
![]() $1$
. Denote by
$1$
. Denote by
![]() $\mathbb{F}$
the algebraic closure of
$\mathbb{F}$
the algebraic closure of
![]() $\mathbb{F}_{\mathfrak{p}}$
. Then the degree of the specialization
$\mathbb{F}_{\mathfrak{p}}$
. Then the degree of the specialization
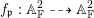 $f_{\mathfrak{p}}:\mathbb{A}_{\mathbb{F}}^{2}{\dashrightarrow}\mathbb{A}_{\mathbb{F}}^{2}$
of
$f_{\mathfrak{p}}:\mathbb{A}_{\mathbb{F}}^{2}{\dashrightarrow}\mathbb{A}_{\mathbb{F}}^{2}$
of
![]() $f$
equals
$f$
equals
![]() $\operatorname{deg}f$
.
$\operatorname{deg}f$
.
By [Reference XieXie15b, Proposition 6.2], there exists a noncritical periodic point
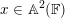 $x\in \mathbb{A}^{2}(\mathbb{F})$
. After replacing
$x\in \mathbb{A}^{2}(\mathbb{F})$
. After replacing
![]() $\mathbb{Q}_{p}$
by a finite extension
$\mathbb{Q}_{p}$
by a finite extension
![]() $K_{\mathfrak{p}}$
, we may suppose that
$K_{\mathfrak{p}}$
, we may suppose that
![]() $x$
is defined over
$x$
is defined over
![]() $O_{K_{\mathfrak{p}}}/\mathfrak{p}$
. Replacing
$O_{K_{\mathfrak{p}}}/\mathfrak{p}$
. Replacing
![]() $f$
by a suitable iterate, we may suppose that
$f$
by a suitable iterate, we may suppose that
![]() $x$
is fixed. Since
$x$
is fixed. Since
![]() $x$
is noncritical,
$x$
is noncritical,
![]() $df_{\mathfrak{p}}(x)$
is invertible. After replacing
$df_{\mathfrak{p}}(x)$
is invertible. After replacing
![]() $f$
by a suitable iterate, we may suppose that
$f$
by a suitable iterate, we may suppose that
 $df_{\mathfrak{p}}(x)=\operatorname{id}$
.
$df_{\mathfrak{p}}(x)=\operatorname{id}$
.
The fixed point
![]() $x$
defines an open and closed neighborhood
$x$
defines an open and closed neighborhood
![]() $U$
in
$U$
in
![]() $\mathbb{A}^{2}(K_{\mathfrak{p}})$
with respect to
$\mathbb{A}^{2}(K_{\mathfrak{p}})$
with respect to
![]() $d_{\mathfrak{p}}$
such that
$d_{\mathfrak{p}}$
such that
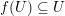 $f(U)\subseteq U$
. By applying [Reference PoonenPoo14, Theorem 1], we have that for any point
$f(U)\subseteq U$
. By applying [Reference PoonenPoo14, Theorem 1], we have that for any point
![]() $q\in U$
, there exists a
$q\in U$
, there exists a
![]() $\mathfrak{p}$
-adic analytic map
$\mathfrak{p}$
-adic analytic map
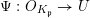 $\unicode[STIX]{x1D6F9}:O_{K_{\mathfrak{p}}}\rightarrow U$
such that for any
$\unicode[STIX]{x1D6F9}:O_{K_{\mathfrak{p}}}\rightarrow U$
such that for any
![]() $n\geqslant 0$
, we have
$n\geqslant 0$
, we have
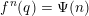 $f^{n}(q)=\unicode[STIX]{x1D6F9}(n)$
.
$f^{n}(q)=\unicode[STIX]{x1D6F9}(n)$
.
Arguing by contradiction, we suppose that the orbit
![]() $O(q)$
of
$O(q)$
of
![]() $q$
is not Zariski dense for any
$q$
is not Zariski dense for any
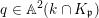 $q\in \mathbb{A}^{2}(k\cap K_{\mathfrak{p}})$
. As in the proof of Lemma 6.2, if
$q\in \mathbb{A}^{2}(k\cap K_{\mathfrak{p}})$
. As in the proof of Lemma 6.2, if
![]() $q$
is preperiodic, then
$q$
is preperiodic, then
![]() $q$
is fixed. Suppose that
$q$
is fixed. Suppose that
![]() $q$
is nonpreperiodic. There exists an irreducible curve
$q$
is nonpreperiodic. There exists an irreducible curve
![]() $C$
such that
$C$
such that
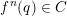 $f^{n}(q)\in C$
for infinitely many
$f^{n}(q)\in C$
for infinitely many
![]() $n\geqslant 0$
. Let
$n\geqslant 0$
. Let
![]() $P$
be a polynomial such that
$P$
be a polynomial such that
![]() $C$
is defined by
$C$
is defined by
![]() $P=0$
. Then
$P=0$
. Then
![]() $P\circ \unicode[STIX]{x1D6F9}$
is an analytic function on
$P\circ \unicode[STIX]{x1D6F9}$
is an analytic function on
![]() $O_{K_{\mathfrak{p}}}$
having infinitely many zeros. It follows that
$O_{K_{\mathfrak{p}}}$
having infinitely many zeros. It follows that
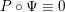 $P\circ \unicode[STIX]{x1D6F9}\equiv 0$
and then
$P\circ \unicode[STIX]{x1D6F9}\equiv 0$
and then
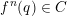 $f^{n}(q)\in C$
for all
$f^{n}(q)\in C$
for all
![]() $n\geqslant 0$
. Then we have
$n\geqslant 0$
. Then we have
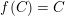 $f(C)=C$
. Since
$f(C)=C$
. Since
![]() $f$
is birational, a curve
$f$
is birational, a curve
![]() $C$
is totally invariant by
$C$
is totally invariant by
![]() $f$
if and only if
$f$
if and only if
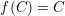 $f(C)=C$
. We may suppose that
$f(C)=C$
. We may suppose that
![]() $f\neq \operatorname{id}$
. Since
$f\neq \operatorname{id}$
. Since
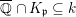 $\overline{\mathbb{Q}}\cap K_{\mathfrak{p}}\subseteq k$
and the
$\overline{\mathbb{Q}}\cap K_{\mathfrak{p}}\subseteq k$
and the
![]() $\overline{\mathbb{Q}}\cap K_{\mathfrak{p}}$
-points in
$\overline{\mathbb{Q}}\cap K_{\mathfrak{p}}$
-points in
![]() $U$
are Zariski dense in
$U$
are Zariski dense in
![]() $\mathbb{A}_{K_{\mathfrak{p}}}^{2}$
, there are infinitely many irreducible totally invariant curves in
$\mathbb{A}_{K_{\mathfrak{p}}}^{2}$
, there are infinitely many irreducible totally invariant curves in
![]() $\mathbb{A}^{2}$
. We conclude our corollary by invoking Proposition 7.1.◻
$\mathbb{A}^{2}$
. We conclude our corollary by invoking Proposition 7.1.◻
8 Proof of Theorem 1.1
Let
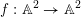 $f:\mathbb{A}^{2}\rightarrow \mathbb{A}^{2}$
be a dominant polynomial endomorphism defined over an algebraically closed field
$f:\mathbb{A}^{2}\rightarrow \mathbb{A}^{2}$
be a dominant polynomial endomorphism defined over an algebraically closed field
![]() $k$
of characteristic
$k$
of characteristic
![]() $0$
.
$0$
.
After replacing
![]() $k$
by an algebraically closed subfield which contains all the coefficients of
$k$
by an algebraically closed subfield which contains all the coefficients of
![]() $f$
, we may suppose that the transcendence degree of
$f$
, we may suppose that the transcendence degree of
![]() $k$
over
$k$
over
![]() $\bar{\mathbb{Q}}$
is finite.
$\bar{\mathbb{Q}}$
is finite.
By Lemma 6.1, Proposition 6.3 and Corollary 7.2, we may suppose that
 $\unicode[STIX]{x1D706}_{1}^{2}>\unicode[STIX]{x1D706}_{2}>1$
and
$\unicode[STIX]{x1D706}_{1}^{2}>\unicode[STIX]{x1D706}_{2}>1$
and
![]() $v_{\ast }$
is divisorial. Suppose that
$v_{\ast }$
is divisorial. Suppose that
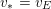 $v_{\ast }=v_{E}$
for some irreducible exceptional divisor
$v_{\ast }=v_{E}$
for some irreducible exceptional divisor
![]() $E$
in some compactification
$E$
in some compactification
![]() $X$
. If
$X$
. If
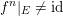 $f^{n}|_{E}\neq \operatorname{id}$
for all
$f^{n}|_{E}\neq \operatorname{id}$
for all
![]() $n\geqslant 1$
, Lemma 6.2 concludes the proof. So, after replacing
$n\geqslant 1$
, Lemma 6.2 concludes the proof. So, after replacing
![]() $f$
by a suitable iterate, we may suppose that
$f$
by a suitable iterate, we may suppose that
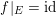 $f|_{E}=\operatorname{id}$
.
$f|_{E}=\operatorname{id}$
.
By choosing a suitable compactification
![]() $X\in {\mathcal{C}}_{0}$
, we may suppose that
$X\in {\mathcal{C}}_{0}$
, we may suppose that
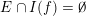 $E\cap I(f)=\emptyset$
. There exists a subfield
$E\cap I(f)=\emptyset$
. There exists a subfield
![]() $K$
of
$K$
of
![]() $k$
which is finitely generated over
$k$
which is finitely generated over
![]() $\mathbb{Q}$
such that
$\mathbb{Q}$
such that
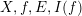 $X,f,E,I(f)$
are defined over
$X,f,E,I(f)$
are defined over
![]() $K$
. Moreover, we may suppose that
$K$
. Moreover, we may suppose that
![]() $E\simeq \mathbb{P}^{1}$
over
$E\simeq \mathbb{P}^{1}$
over
![]() $K$
.
$K$
.
By [Reference BellBel06, Lemma 3.1], there exists a prime
![]() $\mathfrak{p}\geqslant 3$
such that we can embed
$\mathfrak{p}\geqslant 3$
such that we can embed
![]() $K$
into
$K$
into
![]() $\mathbb{Q}_{\mathfrak{p}}$
. Further, there exists an open and closed set
$\mathbb{Q}_{\mathfrak{p}}$
. Further, there exists an open and closed set
![]() $U$
of
$U$
of
![]() $X(\mathbb{Q}_{\mathfrak{p}})$
with respect to the norm
$X(\mathbb{Q}_{\mathfrak{p}})$
with respect to the norm
![]() $|\cdot |_{\mathfrak{p}}$
containing
$|\cdot |_{\mathfrak{p}}$
containing
![]() $E$
and satisfying
$E$
and satisfying
 $U\cap I(f)=\emptyset$
,
$U\cap I(f)=\emptyset$
,
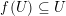 $f(U)\subseteq U$
and
$f(U)\subseteq U$
and
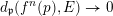 $d_{\mathfrak{p}}(f^{n}(p),E)\rightarrow 0$
as
$d_{\mathfrak{p}}(f^{n}(p),E)\rightarrow 0$
as
![]() $n\rightarrow \infty$
for any
$n\rightarrow \infty$
for any
![]() $p\in U$
.
$p\in U$
.
By [Reference AbateAba01, Theorem 3.1.4], for any point
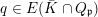 $q\in E(\bar{K}\cap Q_{\mathfrak{p}})$
, there is at most one irreducible algebraic curve
$q\in E(\bar{K}\cap Q_{\mathfrak{p}})$
, there is at most one irreducible algebraic curve
![]() $C_{q}\neq E$
in
$C_{q}\neq E$
in
![]() $X$
such that
$X$
such that
![]() $q\in C_{q}$
and
$q\in C_{q}$
and
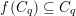 $f(C_{q})\subseteq C_{q}$
. For convenience, if such an algebraic curve does not exist, set
$f(C_{q})\subseteq C_{q}$
. For convenience, if such an algebraic curve does not exist, set
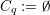 $C_{q}:=\emptyset$
. Further, if
$C_{q}:=\emptyset$
. Further, if
![]() $C_{q}\neq \emptyset$
,
$C_{q}\neq \emptyset$
,
![]() $C_{q}$
is smooth at
$C_{q}$
is smooth at
![]() $q$
and intersects
$q$
and intersects
![]() $E$
transitively.
$E$
transitively.
If there are only finitely many points
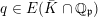 $q\in E(\bar{K}\cap \mathbb{Q}_{\mathfrak{p}})$
such that
$q\in E(\bar{K}\cap \mathbb{Q}_{\mathfrak{p}})$
such that
![]() $C_{q}$
is an algebraic curve, there exist a point
$C_{q}$
is an algebraic curve, there exist a point
![]() $q\in E$
and an open and closed set
$q\in E$
and an open and closed set
![]() $V$
with respect to the norm
$V$
with respect to the norm
![]() $|\cdot |_{\mathfrak{p}}$
containing
$|\cdot |_{\mathfrak{p}}$
containing
![]() $q$
such that
$q$
such that
 $f(V)\subseteq V$
and
$f(V)\subseteq V$
and
![]() $C_{x}=\emptyset$
for all
$C_{x}=\emptyset$
for all
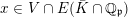 $x\in V\cap E(\bar{K}\cap \mathbb{Q}_{\mathfrak{p}})$
. Pick a point
$x\in V\cap E(\bar{K}\cap \mathbb{Q}_{\mathfrak{p}})$
. Pick a point
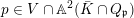 $p\in V\cap \mathbb{A}^{2}(\bar{K}\cap Q_{\mathfrak{p}})$
; then
$p\in V\cap \mathbb{A}^{2}(\bar{K}\cap Q_{\mathfrak{p}})$
; then
![]() $p$
is not preperiodic. If
$p$
is not preperiodic. If
![]() $O(p)$
is not Zariski dense, we denote by
$O(p)$
is not Zariski dense, we denote by
![]() $Z$
its Zariski closure. There exists a one-dimensional irreducible component
$Z$
its Zariski closure. There exists a one-dimensional irreducible component
![]() $C$
of
$C$
of
![]() $Z$
which is periodic under
$Z$
which is periodic under
![]() $f$
. Since
$f$
. Since
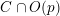 $C\cap O(p)$
is infinite,
$C\cap O(p)$
is infinite,
![]() $C$
is defined over
$C$
is defined over
![]() $\bar{K}\cap Q_{\mathfrak{p}}$
. Since
$\bar{K}\cap Q_{\mathfrak{p}}$
. Since
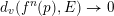 $d_{v}(f^{n}(p),E)\rightarrow 0$
as
$d_{v}(f^{n}(p),E)\rightarrow 0$
as
![]() $n\rightarrow \infty$
, we have
$n\rightarrow \infty$
, we have
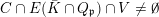 $C\cap E(\bar{K}\cap Q_{\mathfrak{p}})\cap V\neq \emptyset$
. Pick
$C\cap E(\bar{K}\cap Q_{\mathfrak{p}})\cap V\neq \emptyset$
. Pick
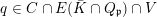 $q\in C\cap E(\bar{K}\cap Q_{\mathfrak{p}})\cap V$
; then we have that
$q\in C\cap E(\bar{K}\cap Q_{\mathfrak{p}})\cap V$
; then we have that
![]() $C_{q}=C$
is an algebraic curve, which contradicts our assumption. Thus,
$C_{q}=C$
is an algebraic curve, which contradicts our assumption. Thus,
![]() $O(p)$
is Zariski dense.
$O(p)$
is Zariski dense.
Otherwise there exists an infinite sequence of points
![]() $q_{i}$
,
$q_{i}$
,
![]() $i\geqslant 1$
, such that
$i\geqslant 1$
, such that
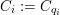 $C_{i}:=C_{q_{i}}$
is an algebraic curve. Since
$C_{i}:=C_{q_{i}}$
is an algebraic curve. Since
![]() $f|_{C_{i}}$
is an endomorphism of
$f|_{C_{i}}$
is an endomorphism of
![]() $C_{i}$
of degree
$C_{i}$
of degree
![]() $\unicode[STIX]{x1D706}_{1}>1$
, every
$\unicode[STIX]{x1D706}_{1}>1$
, every
![]() $C_{i}$
is rational and has at most two branches at infinity. We may suppose that
$C_{i}$
is rational and has at most two branches at infinity. We may suppose that
![]() $E$
is the unique irreducible component of
$E$
is the unique irreducible component of
![]() $X\setminus \mathbb{A}^{2}$
containing
$X\setminus \mathbb{A}^{2}$
containing
![]() $q_{i}$
for all
$q_{i}$
for all
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
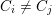 $C_{i}\neq C_{j}$
for
$C_{i}\neq C_{j}$
for
![]() $i\neq j$
. We need the following result, which is proved below.
$i\neq j$
. We need the following result, which is proved below.
Lemma 8.1. After replacing
![]() $\{C_{i}\}_{i\geqslant 1}$
by an infinite subsequence, we have that either
$\{C_{i}\}_{i\geqslant 1}$
by an infinite subsequence, we have that either
![]() $\operatorname{deg}(C_{i})$
is bounded or Theorem 1.1 holds.
$\operatorname{deg}(C_{i})$
is bounded or Theorem 1.1 holds.
Suppose that
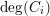 $\operatorname{deg}(C_{i})$
is bounded. Pick an ample line bundle
$\operatorname{deg}(C_{i})$
is bounded. Pick an ample line bundle
![]() $L$
on
$L$
on
![]() $X$
. Then there exists
$X$
. Then there exists
![]() $M>0$
such that
$M>0$
such that
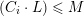 $(C_{i}\cdot L)\leqslant M$
for all
$(C_{i}\cdot L)\leqslant M$
for all
![]() $i\geqslant 1$
.
$i\geqslant 1$
.
There exist a smooth projective surface
![]() $\unicode[STIX]{x1D6E4}$
, a birational morphism
$\unicode[STIX]{x1D6E4}$
, a birational morphism
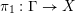 $\unicode[STIX]{x1D70B}_{1}:\unicode[STIX]{x1D6E4}\rightarrow X$
and a morphism
$\unicode[STIX]{x1D70B}_{1}:\unicode[STIX]{x1D6E4}\rightarrow X$
and a morphism
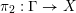 $\unicode[STIX]{x1D70B}_{2}:\unicode[STIX]{x1D6E4}\rightarrow X$
satisfying
$\unicode[STIX]{x1D70B}_{2}:\unicode[STIX]{x1D6E4}\rightarrow X$
satisfying
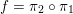 $f=\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1}$
. We denote by
$f=\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1}$
. We denote by
![]() $f_{\ast }$
the map
$f_{\ast }$
the map
 $\unicode[STIX]{x1D70B}_{2\ast }\circ \unicode[STIX]{x1D70B}_{1}^{\ast }:\operatorname{Div}X\rightarrow \operatorname{Div}X$
. Let
$\unicode[STIX]{x1D70B}_{2\ast }\circ \unicode[STIX]{x1D70B}_{1}^{\ast }:\operatorname{Div}X\rightarrow \operatorname{Div}X$
. Let
![]() $E_{\unicode[STIX]{x1D70B}_{1}}$
be the union of exceptional irreducible divisors of
$E_{\unicode[STIX]{x1D70B}_{1}}$
be the union of exceptional irreducible divisors of
![]() $\unicode[STIX]{x1D70B}_{1}$
and
$\unicode[STIX]{x1D70B}_{1}$
and
![]() $\mathfrak{E}$
be the set of effective divisors in
$\mathfrak{E}$
be the set of effective divisors in
![]() $X$
supported by
$X$
supported by
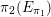 $\unicode[STIX]{x1D70B}_{2}(E_{\unicode[STIX]{x1D70B}_{1}})$
. It follows that for any curve
$\unicode[STIX]{x1D70B}_{2}(E_{\unicode[STIX]{x1D70B}_{1}})$
. It follows that for any curve
![]() $C$
in
$C$
in
![]() $X$
, there exists
$X$
, there exists
![]() $D\in \mathfrak{E}$
such that
$D\in \mathfrak{E}$
such that
 $f_{\ast }C=\operatorname{deg}(f|_{C})f(C)+D$
.
$f_{\ast }C=\operatorname{deg}(f|_{C})f(C)+D$
.
For any effective line bundle
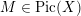 $M\in \operatorname{Pic}(X)$
, the projective space
$M\in \operatorname{Pic}(X)$
, the projective space
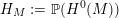 $H_{M}:=\mathbb{P}(H^{0}(M))$
parameterizes the curves
$H_{M}:=\mathbb{P}(H^{0}(M))$
parameterizes the curves
![]() $C$
in the linear system
$C$
in the linear system
![]() $|M|$
. Since
$|M|$
. Since
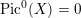 $\operatorname{Pic}^{0}(X)=0$
, for any
$\operatorname{Pic}^{0}(X)=0$
, for any
![]() $l\geqslant 0$
, there are only finitely many effective line bundles satisfying
$l\geqslant 0$
, there are only finitely many effective line bundles satisfying
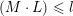 $(M\cdot L)\leqslant l$
.
$(M\cdot L)\leqslant l$
.
Then
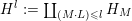 $H^{l}:=\coprod _{(M\cdot L)\leqslant l}H_{M}$
is a finite union of projective spaces and it parameterizes the curves
$H^{l}:=\coprod _{(M\cdot L)\leqslant l}H_{M}$
is a finite union of projective spaces and it parameterizes the curves
![]() $C$
in
$C$
in
![]() $X$
satisfying
$X$
satisfying
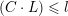 $(C\cdot L)\leqslant l$
.
$(C\cdot L)\leqslant l$
.
There exists
![]() $d\geqslant 1$
such that
$d\geqslant 1$
such that
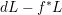 $dL-f^{\ast }L$
is nef. Then, for any curve
$dL-f^{\ast }L$
is nef. Then, for any curve
![]() $C$
in
$C$
in
![]() $X$
, we have
$X$
, we have
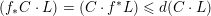 $(f_{\ast }C\cdot L)=(C\cdot f^{\ast }L)\leqslant d(C\cdot L)$
. It follows that
$(f_{\ast }C\cdot L)=(C\cdot f^{\ast }L)\leqslant d(C\cdot L)$
. It follows that
![]() $f_{\ast }$
induces a morphism
$f_{\ast }$
induces a morphism
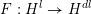 $F:H^{l}\rightarrow H^{dl}$
by
$F:H^{l}\rightarrow H^{dl}$
by
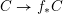 $C\rightarrow f_{\ast }C$
for all
$C\rightarrow f_{\ast }C$
for all
![]() $l\geqslant 1$
. For all
$l\geqslant 1$
. For all
![]() $l\geqslant 1$
,
$l\geqslant 1$
,
![]() $a\in \mathbb{Z}^{+}$
and
$a\in \mathbb{Z}^{+}$
and
![]() $D\in \mathfrak{E}$
, there exists an embedding
$D\in \mathfrak{E}$
, there exists an embedding
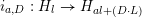 $i_{a,D}:H_{l}\rightarrow H_{al+(D\cdot L)}$
by
$i_{a,D}:H_{l}\rightarrow H_{al+(D\cdot L)}$
by
 $C\mapsto aC+D$
. Let
$C\mapsto aC+D$
. Let
 $Z_{1},\ldots ,Z_{m}$
be all irreducible components of the Zariski closure of
$Z_{1},\ldots ,Z_{m}$
be all irreducible components of the Zariski closure of
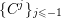 $\{C^{j}\}_{j\leqslant -1}$
in
$\{C^{j}\}_{j\leqslant -1}$
in
![]() $H^{M}$
of maximal dimension. For any
$H^{M}$
of maximal dimension. For any
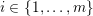 $i\in \{1,\ldots ,m\}$
, there exists
$i\in \{1,\ldots ,m\}$
, there exists
![]() $l\leqslant M$
such that
$l\leqslant M$
such that
 $(C\cdot L)=l$
for all
$(C\cdot L)=l$
for all
![]() $C\in Z_{i}$
. Let
$C\in Z_{i}$
. Let
![]() $S$
be the finite set of pairs
$S$
be the finite set of pairs
![]() $(a,D)$
, where
$(a,D)$
, where
![]() $a\in \mathbb{Z}^{+}$
,
$a\in \mathbb{Z}^{+}$
,
![]() $D\in \mathfrak{E}$
satisfying
$D\in \mathfrak{E}$
satisfying
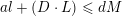 $al+(D\cdot L)\leqslant dM$
. Then we have
$al+(D\cdot L)\leqslant dM$
. Then we have
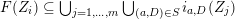 $F(Z_{i})\subseteq \bigcup _{j=1,\ldots ,m}\bigcup _{(a,D)\in S}i_{a,D}(Z_{j})$
. It follows that there exist a unique
$F(Z_{i})\subseteq \bigcup _{j=1,\ldots ,m}\bigcup _{(a,D)\in S}i_{a,D}(Z_{j})$
. It follows that there exist a unique
 $j_{i}\in \{1,\ldots ,m\}$
and a unique
$j_{i}\in \{1,\ldots ,m\}$
and a unique
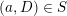 $(a,D)\in S$
such that
$(a,D)\in S$
such that
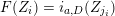 $F(Z_{i})=i_{a,D}(Z_{j_{i}})$
. Observe that the map
$F(Z_{i})=i_{a,D}(Z_{j_{i}})$
. Observe that the map
![]() $i\mapsto j_{i}$
is a one to one map of
$i\mapsto j_{i}$
is a one to one map of
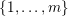 $\{1,\ldots ,m\}$
. After replacing
$\{1,\ldots ,m\}$
. After replacing
![]() $f$
by a positive iterate, we may suppose that
$f$
by a positive iterate, we may suppose that
![]() $j_{i}=i$
and
$j_{i}=i$
and
 $F(Z_{i})\subseteq i_{a_{Z_{i}},D_{Z_{i}}}Z_{i}$
for all
$F(Z_{i})\subseteq i_{a_{Z_{i}},D_{Z_{i}}}Z_{i}$
for all
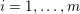 $i=1,\ldots ,m$
. Set
$i=1,\ldots ,m$
. Set
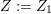 $Z:=Z_{1}$
,
$Z:=Z_{1}$
,
![]() $a=a_{Z_{1}}$
and
$a=a_{Z_{1}}$
and
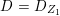 $D=D_{Z_{1}}$
. We may suppose that
$D=D_{Z_{1}}$
. We may suppose that
![]() $C_{i}\in Z$
for all
$C_{i}\in Z$
for all
![]() $i\geqslant 1$
. Since
$i\geqslant 1$
. Since
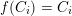 $f(C_{i})=C_{i}$
for all
$f(C_{i})=C_{i}$
for all
![]() $i\geqslant 1$
, we have
$i\geqslant 1$
, we have
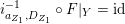 $i_{a_{Z_{1}},D_{Z_{1}}}^{-1}\circ F|_{Y}=\operatorname{id}$
.
$i_{a_{Z_{1}},D_{Z_{1}}}^{-1}\circ F|_{Y}=\operatorname{id}$
.
For any point
![]() $t\in Z$
, denote by
$t\in Z$
, denote by
![]() $C^{t}$
the curve parameterized by
$C^{t}$
the curve parameterized by
![]() $t$
. Then
$t$
. Then
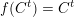 $f(C^{t})=C^{t}$
for all
$f(C^{t})=C^{t}$
for all
![]() $t\in Z$
. Since
$t\in Z$
. Since
![]() $C_{i}$
intersects
$C_{i}$
intersects
![]() $E$
transversely at at most two points, there exists
$E$
transversely at at most two points, there exists
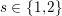 $s\in \{1,2\}$
such that
$s\in \{1,2\}$
such that
![]() $C^{t}$
intersects
$C^{t}$
intersects
![]() $E$
transversely at
$E$
transversely at
![]() $s$
points for a general
$s$
points for a general
![]() $t\in Z$
. It follows that, for a general point
$t\in Z$
. It follows that, for a general point
![]() $t\in Z$
, there are exactly
$t\in Z$
, there are exactly
![]() $s$
points
$s$
points
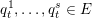 $q_{t}^{1},\ldots ,q_{t}^{s}\in E$
such that
$q_{t}^{1},\ldots ,q_{t}^{s}\in E$
such that
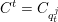 $C^{t}=C_{q_{t}^{j}}$
for
$C^{t}=C_{q_{t}^{j}}$
for
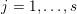 $j=1,\ldots ,s$
.
$j=1,\ldots ,s$
.
Set
 $Y:=\{(p,t)\in X\times Z\mid p\in C^{t}\}$
. Denote by
$Y:=\{(p,t)\in X\times Z\mid p\in C^{t}\}$
. Denote by
 $\unicode[STIX]{x1D70B}_{1}:Y\rightarrow X$
the projection to the first coordinate and by
$\unicode[STIX]{x1D70B}_{1}:Y\rightarrow X$
the projection to the first coordinate and by
 $\unicode[STIX]{x1D70B}_{2}:Y\rightarrow Z$
the projection to the second coordinate. Since
$\unicode[STIX]{x1D70B}_{2}:Y\rightarrow Z$
the projection to the second coordinate. Since
![]() $C^{t}\cap E$
is not empty for general
$C^{t}\cap E$
is not empty for general
![]() $t\in Z$
, the map
$t\in Z$
, the map
![]() $\unicode[STIX]{x1D70B}_{2}|_{\unicode[STIX]{x1D70B}_{1}^{\ast }E}$
is dominant. We see that
$\unicode[STIX]{x1D70B}_{2}|_{\unicode[STIX]{x1D70B}_{1}^{\ast }E}$
is dominant. We see that
![]() $f$
induces a map
$f$
induces a map
 $T:Y\rightarrow Y$
defined by
$T:Y\rightarrow Y$
defined by
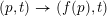 $(p,t)\rightarrow (f(p),t)$
. Since there are infinitely many points in
$(p,t)\rightarrow (f(p),t)$
. Since there are infinitely many points in
![]() $E$
contained in
$E$
contained in
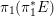 $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D70B}_{1}^{\ast }E)$
,
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D70B}_{1}^{\ast }E)$
,
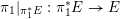 $\unicode[STIX]{x1D70B}_{1}|_{\unicode[STIX]{x1D70B}_{1}^{\ast }E}:\unicode[STIX]{x1D70B}_{1}^{\ast }E\rightarrow E$
is dominant. For a general point
$\unicode[STIX]{x1D70B}_{1}|_{\unicode[STIX]{x1D70B}_{1}^{\ast }E}:\unicode[STIX]{x1D70B}_{1}^{\ast }E\rightarrow E$
is dominant. For a general point
![]() $t\in Z$
, there are exactly
$t\in Z$
, there are exactly
![]() $s$
points in
$s$
points in
![]() $\unicode[STIX]{x1D70B}_{1}^{\ast }E$
. It follows that the map
$\unicode[STIX]{x1D70B}_{1}^{\ast }E$
. It follows that the map
![]() $\unicode[STIX]{x1D70B}_{2}|_{\unicode[STIX]{x1D70B}_{1}^{\ast }E}$
is generically finite of degree
$\unicode[STIX]{x1D70B}_{2}|_{\unicode[STIX]{x1D70B}_{1}^{\ast }E}$
is generically finite of degree
![]() $s$
. For a general point
$s$
. For a general point
![]() $q\in E$
, there exists only one point
$q\in E$
, there exists only one point
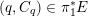 $(q,C_{q})\in \unicode[STIX]{x1D70B}_{1}^{\ast }E$
. Hence,
$(q,C_{q})\in \unicode[STIX]{x1D70B}_{1}^{\ast }E$
. Hence,
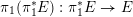 $\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D70B}_{1}^{\ast }E):\unicode[STIX]{x1D70B}_{1}^{\ast }E\rightarrow E$
is birational. It follows that
$\unicode[STIX]{x1D70B}_{1}(\unicode[STIX]{x1D70B}_{1}^{\ast }E):\unicode[STIX]{x1D70B}_{1}^{\ast }E\rightarrow E$
is birational. It follows that
![]() $Z$
is a rational curve and
$Z$
is a rational curve and
![]() $Y$
is a surface. Thus, the morphism
$Y$
is a surface. Thus, the morphism
 $\unicode[STIX]{x1D70B}_{1}:Y\rightarrow X$
is generically finite. Let
$\unicode[STIX]{x1D70B}_{1}:Y\rightarrow X$
is generically finite. Let
![]() $p$
be a general point in
$p$
be a general point in
![]() $\mathbb{A}^{2}$
. If
$\mathbb{A}^{2}$
. If
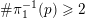 $\#\unicode[STIX]{x1D70B}_{1}^{-1}(p)\geqslant 2$
, then there are
$\#\unicode[STIX]{x1D70B}_{1}^{-1}(p)\geqslant 2$
, then there are
 $t_{1}\neq t_{2}\in Z$
such that
$t_{1}\neq t_{2}\in Z$
such that
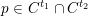 $p\in C^{t_{1}}\cap C^{t_{2}}$
. Since there exists
$p\in C^{t_{1}}\cap C^{t_{2}}$
. Since there exists
![]() $M^{\prime }>0$
such that
$M^{\prime }>0$
such that
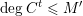 $\operatorname{deg}C^{t}\leqslant M^{\prime }$
for all
$\operatorname{deg}C^{t}\leqslant M^{\prime }$
for all
![]() $t\in Z$
, we have
$t\in Z$
, we have
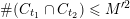 $\#(C_{t_{1}}\cap C_{t_{2}})\leqslant {M^{\prime }}^{2}$
. It follows that there exist
$\#(C_{t_{1}}\cap C_{t_{2}})\leqslant {M^{\prime }}^{2}$
. It follows that there exist
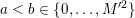 $a<b\in \{0,\ldots ,{M^{\prime }}^{2}\}$
such that
$a<b\in \{0,\ldots ,{M^{\prime }}^{2}\}$
such that
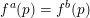 $f^{a}(p)=f^{b}(p)$
. This contradicts the assumption that
$f^{a}(p)=f^{b}(p)$
. This contradicts the assumption that
![]() $p$
is general. It follows that the morphism
$p$
is general. It follows that the morphism
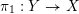 $\unicode[STIX]{x1D70B}_{1}:Y\rightarrow X$
is birational. Identify
$\unicode[STIX]{x1D70B}_{1}:Y\rightarrow X$
is birational. Identify
![]() $Z$
with
$Z$
with
![]() $\mathbb{P}^{1}$
. Set
$\mathbb{P}^{1}$
. Set
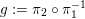 $g:=\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1}^{-1}$
. Then we have
$g:=\unicode[STIX]{x1D70B}_{2}\circ \unicode[STIX]{x1D70B}_{1}^{-1}$
. Then we have
 $g\circ f=g$
, which completes the proof.
$g\circ f=g$
, which completes the proof.
Proof of Lemma 8.1.
If
![]() $C_{i}$
has only one place at infinity for all
$C_{i}$
has only one place at infinity for all
![]() $i\geqslant 1$
, then
$i\geqslant 1$
, then
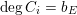 $\operatorname{deg}C_{i}=b_{E}$
. So, we may suppose that
$\operatorname{deg}C_{i}=b_{E}$
. So, we may suppose that
![]() $C_{i}$
has two places at infinity for all
$C_{i}$
has two places at infinity for all
![]() $i\geqslant 1$
.
$i\geqslant 1$
.
We first suppose that
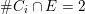 $\#C_{i}\cap E=2$
for all
$\#C_{i}\cap E=2$
for all
![]() $i\geqslant 1$
. We may suppose that
$i\geqslant 1$
. We may suppose that
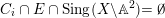 $C_{i}\cap E\cap \operatorname{Sing}(X\setminus \mathbb{A}^{2})=\emptyset$
for all
$C_{i}\cap E\cap \operatorname{Sing}(X\setminus \mathbb{A}^{2})=\emptyset$
for all
![]() $i\geqslant 1$
. Then, for all
$i\geqslant 1$
. Then, for all
![]() $i\geqslant 1$
, we have
$i\geqslant 1$
, we have
 $\operatorname{deg}C_{i}=2b_{E}$
.
$\operatorname{deg}C_{i}=2b_{E}$
.
Then we may suppose that
 $C_{i}\cap E=\{q_{i}\}$
for all
$C_{i}\cap E=\{q_{i}\}$
for all
![]() $i\geqslant 1$
. Let
$i\geqslant 1$
. Let
![]() $c_{i}$
be the unique branch of
$c_{i}$
be the unique branch of
![]() $C$
at infinity centered at
$C$
at infinity centered at
![]() $q_{i}$
and
$q_{i}$
and
![]() $w_{i}$
the unique branch of
$w_{i}$
the unique branch of
![]() $C$
at infinity not centred at
$C$
at infinity not centred at
![]() $q_{i}$
. Since
$q_{i}$
. Since
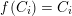 $f(C_{i})=C_{i}$
, we have
$f(C_{i})=C_{i}$
, we have
 $f_{\bullet }(c_{i})=c_{i}$
and
$f_{\bullet }(c_{i})=c_{i}$
and
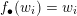 $f_{\bullet }(w_{i})=w_{i}$
.
$f_{\bullet }(w_{i})=w_{i}$
.
We first treat the case
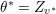 $\unicode[STIX]{x1D703}^{\ast }=Z_{v^{\ast }}$
, where
$\unicode[STIX]{x1D703}^{\ast }=Z_{v^{\ast }}$
, where
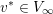 $v^{\ast }\in V_{\infty }$
is divisorial. It follows that
$v^{\ast }\in V_{\infty }$
is divisorial. It follows that
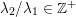 $\unicode[STIX]{x1D706}_{2}/\unicode[STIX]{x1D706}_{1}\in \mathbb{Z}^{+}$
. Observe that
$\unicode[STIX]{x1D706}_{2}/\unicode[STIX]{x1D706}_{1}\in \mathbb{Z}^{+}$
. Observe that
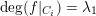 $\operatorname{deg}(f|_{C_{i}})=\unicode[STIX]{x1D706}_{1}$
for
$\operatorname{deg}(f|_{C_{i}})=\unicode[STIX]{x1D706}_{1}$
for
![]() $i$
large enough.
$i$
large enough.
If
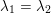 $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}$
, then the strict transform
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}_{2}$
, then the strict transform
![]() $f^{\#}(C_{i})$
equals
$f^{\#}(C_{i})$
equals
![]() $C_{i}$
for
$C_{i}$
for
![]() $i$
large enough, and the lemma follows from Proposition 7.1.
$i$
large enough, and the lemma follows from Proposition 7.1.
Otherwise we have
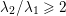 $\unicode[STIX]{x1D706}_{2}/\unicode[STIX]{x1D706}_{1}\geqslant 2$
. Set
$\unicode[STIX]{x1D706}_{2}/\unicode[STIX]{x1D706}_{1}\geqslant 2$
. Set
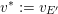 $v^{\ast }:=v_{E^{\prime }}$
. Then we have
$v^{\ast }:=v_{E^{\prime }}$
. Then we have
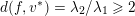 $d(f,v^{\ast })=\unicode[STIX]{x1D706}_{2}/\unicode[STIX]{x1D706}_{1}\geqslant 2$
and
$d(f,v^{\ast })=\unicode[STIX]{x1D706}_{2}/\unicode[STIX]{x1D706}_{1}\geqslant 2$
and
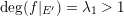 $\operatorname{deg}(f|_{E^{\prime }})=\unicode[STIX]{x1D706}_{1}>1$
. By Lemma 6.2, Theorem 1.1 holds.
$\operatorname{deg}(f|_{E^{\prime }})=\unicode[STIX]{x1D706}_{1}>1$
. By Lemma 6.2, Theorem 1.1 holds.
Next, we treat the case
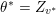 $\unicode[STIX]{x1D703}^{\ast }=Z_{v^{\ast }}$
, where
$\unicode[STIX]{x1D703}^{\ast }=Z_{v^{\ast }}$
, where
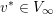 $v^{\ast }\in V_{\infty }$
is not divisorial. Since
$v^{\ast }\in V_{\infty }$
is not divisorial. Since
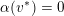 $\unicode[STIX]{x1D6FC}(v^{\ast })=0$
,
$\unicode[STIX]{x1D6FC}(v^{\ast })=0$
,
![]() $v^{\ast }$
cannot be irrational. Thus,
$v^{\ast }$
cannot be irrational. Thus,
![]() $v^{\ast }$
is infinitely singular and hence an end point in
$v^{\ast }$
is infinitely singular and hence an end point in
![]() $V_{\infty }$
. Then
$V_{\infty }$
. Then
![]() $f$
is proper.
$f$
is proper.
By [Reference XieXie15a, Proposition 15.2], there exists
![]() $v_{1}<v^{\ast }$
such that for any valuation
$v_{1}<v^{\ast }$
such that for any valuation
![]() $v\neq v^{\ast }$
in
$v\neq v^{\ast }$
in
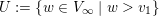 $U:=\{w\in V_{\infty }\mid w>v_{1}\}$
, there exists
$U:=\{w\in V_{\infty }\mid w>v_{1}\}$
, there exists
![]() $N\geqslant 1$
such that
$N\geqslant 1$
such that
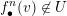 $f_{\bullet }^{n}(v)\not \in U$
for all
$f_{\bullet }^{n}(v)\not \in U$
for all
![]() $n\geqslant N$
. It follows that there is no curve valuation in
$n\geqslant N$
. It follows that there is no curve valuation in
![]() $U$
which is periodic under
$U$
which is periodic under
![]() $f_{\bullet }$
. Let
$f_{\bullet }$
. Let
![]() $U_{E}$
be the open set in
$U_{E}$
be the open set in
![]() $V_{\infty }$
consisting of all valuations whose center in
$V_{\infty }$
consisting of all valuations whose center in
![]() $X$
is contained
$X$
is contained
![]() $E$
. It follows that
$E$
. It follows that
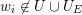 $w_{i}\not \in U\cup U_{E}$
for all
$w_{i}\not \in U\cup U_{E}$
for all
![]() $i\geqslant 1$
. Hence,
$i\geqslant 1$
. Hence,
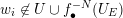 $w_{i}\not \in U\cup f_{\bullet }^{-N}(U_{E})$
for all
$w_{i}\not \in U\cup f_{\bullet }^{-N}(U_{E})$
for all
![]() $N\geqslant 0$
. Set
$N\geqslant 0$
. Set
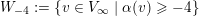 $W_{-4}:=\{v\in V_{\infty }\mid \unicode[STIX]{x1D6FC}(v)\geqslant -4\}$
. By [Reference XieXie15a, Proposition 11.6] and the fact that
$W_{-4}:=\{v\in V_{\infty }\mid \unicode[STIX]{x1D6FC}(v)\geqslant -4\}$
. By [Reference XieXie15a, Proposition 11.6] and the fact that
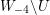 $W_{-4}\setminus U$
is compact, there exists
$W_{-4}\setminus U$
is compact, there exists
![]() $N\geqslant 0$
such that
$N\geqslant 0$
such that
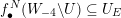 $f_{\bullet }^{N}(W_{-4}\setminus U)\subseteq U_{E}$
. Then we have
$f_{\bullet }^{N}(W_{-4}\setminus U)\subseteq U_{E}$
. Then we have
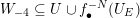 $W_{-4}\subseteq U\cup f_{\bullet }^{-N}(U_{E})$
.
$W_{-4}\subseteq U\cup f_{\bullet }^{-N}(U_{E})$
.
Since the boundary
 $\unicode[STIX]{x2202}(V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E})))$
of
$\unicode[STIX]{x2202}(V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E})))$
of
 $V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E}))$
is finite and
$V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E}))$
is finite and
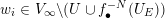 $w_{i}\in V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E}))$
for all
$w_{i}\in V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E}))$
for all
![]() $i\geqslant 1$
, we may suppose that there exists
$i\geqslant 1$
, we may suppose that there exists
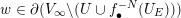 $w\in \unicode[STIX]{x2202}(V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E})))$
satisfying
$w\in \unicode[STIX]{x2202}(V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E})))$
satisfying
![]() $w_{i}>w$
for all
$w_{i}>w$
for all
![]() $i\geqslant 1$
.
$i\geqslant 1$
.
If, for all
![]() $i\geqslant 1$
, we have
$i\geqslant 1$
, we have
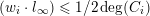 $(w_{i}\cdot l_{\infty })\leqslant 1/2\operatorname{deg}(C_{i})$
, then
$(w_{i}\cdot l_{\infty })\leqslant 1/2\operatorname{deg}(C_{i})$
, then
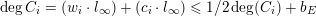 $\operatorname{deg}C_{i}=(w_{i}\cdot l_{\infty })+(c_{i}\cdot l_{\infty })\leqslant 1/2\operatorname{deg}(C_{i})+b_{E}$
. It follows that
$\operatorname{deg}C_{i}=(w_{i}\cdot l_{\infty })+(c_{i}\cdot l_{\infty })\leqslant 1/2\operatorname{deg}(C_{i})+b_{E}$
. It follows that
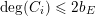 $\operatorname{deg}(C_{i})\leqslant 2b_{E}$
.
$\operatorname{deg}(C_{i})\leqslant 2b_{E}$
.
Thus, we may suppose that
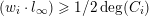 $(w_{i}\cdot l_{\infty })\geqslant 1/2\operatorname{deg}(C_{i})$
for all
$(w_{i}\cdot l_{\infty })\geqslant 1/2\operatorname{deg}(C_{i})$
for all
![]() $i\geqslant 1$
. For any
$i\geqslant 1$
. For any
![]() $i\neq j$
, the intersection number
$i\neq j$
, the intersection number
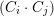 $(C_{i}\cdot C_{j})$
is the sum of the local intersection numbers at all points in
$(C_{i}\cdot C_{j})$
is the sum of the local intersection numbers at all points in
![]() $C_{i}\cap C_{j}$
. Since all the local intersection numbers are positive, we have
$C_{i}\cap C_{j}$
. Since all the local intersection numbers are positive, we have
 $$\begin{eqnarray}\operatorname{deg}(C_{i})\operatorname{deg}(C_{j})\geqslant (c_{i}\cdot c_{j})+(w_{i}\cdot w_{j}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{deg}(C_{i})\operatorname{deg}(C_{j})\geqslant (c_{i}\cdot c_{j})+(w_{i}\cdot w_{j}).\end{eqnarray}$$
By the calculation in § 2.6, we have
 $$\begin{eqnarray}\displaystyle (c_{i}\cdot c_{j})+(w_{i}\cdot w_{j}) & {\geqslant} & \displaystyle b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))+(w_{i}\cdot l_{\infty })(w_{j}\cdot l_{\infty })(1-\unicode[STIX]{x1D6FC}(w))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))+5/4\operatorname{deg}(C_{i})\operatorname{deg}(C_{j}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (c_{i}\cdot c_{j})+(w_{i}\cdot w_{j}) & {\geqslant} & \displaystyle b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))+(w_{i}\cdot l_{\infty })(w_{j}\cdot l_{\infty })(1-\unicode[STIX]{x1D6FC}(w))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))+5/4\operatorname{deg}(C_{i})\operatorname{deg}(C_{j}).\nonumber\end{eqnarray}$$
Thus,
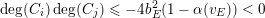 $\operatorname{deg}(C_{i})\operatorname{deg}(C_{j})\leqslant -4b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))<0$
, which is a contradiction.
$\operatorname{deg}(C_{i})\operatorname{deg}(C_{j})\leqslant -4b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))<0$
, which is a contradiction.
Finally, we treat the case when
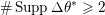 $\#\operatorname{Supp}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}^{\ast }\geqslant 2$
. By [Reference Favre and JonssonFJ11, Theorem 2.4], we have
$\#\operatorname{Supp}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D703}^{\ast }\geqslant 2$
. By [Reference Favre and JonssonFJ11, Theorem 2.4], we have
![]() $\unicode[STIX]{x1D703}^{\ast }>0$
on the set
$\unicode[STIX]{x1D703}^{\ast }>0$
on the set
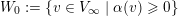 $W_{0}:=\{v\in V_{\infty }\mid \unicode[STIX]{x1D6FC}(v)\geqslant 0\}$
. Set
$W_{0}:=\{v\in V_{\infty }\mid \unicode[STIX]{x1D6FC}(v)\geqslant 0\}$
. Set
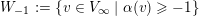 $W_{-1}:=\{v\in V_{\infty }\mid \unicode[STIX]{x1D6FC}(v)\geqslant -1\}$
and
$W_{-1}:=\{v\in V_{\infty }\mid \unicode[STIX]{x1D6FC}(v)\geqslant -1\}$
and
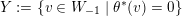 $Y:=\{v\in W_{-1}\mid \unicode[STIX]{x1D703}^{\ast }(v)=0\}$
. By [Reference XieXie15a, Proposition 11.2],
$Y:=\{v\in W_{-1}\mid \unicode[STIX]{x1D703}^{\ast }(v)=0\}$
. By [Reference XieXie15a, Proposition 11.2],
![]() $Y$
is compact. For any point
$Y$
is compact. For any point
![]() $y\in Y$
, there exists
$y\in Y$
, there exists
![]() $w_{y}<y$
satisfying
$w_{y}<y$
satisfying
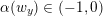 $\unicode[STIX]{x1D6FC}(w_{y})\in (-1,0)$
. Set
$\unicode[STIX]{x1D6FC}(w_{y})\in (-1,0)$
. Set
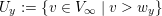 $U_{y}:=\{v\in V_{\infty }\mid v>w_{y}\}$
. There are finitely many points
$U_{y}:=\{v\in V_{\infty }\mid v>w_{y}\}$
. There are finitely many points
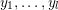 $y_{1},\ldots ,y_{l}$
such that
$y_{1},\ldots ,y_{l}$
such that
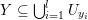 $Y\subseteq \bigcup _{i=1}^{l}U_{y_{i}}$
. Pick
$Y\subseteq \bigcup _{i=1}^{l}U_{y_{i}}$
. Pick
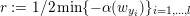 $r:=1/2\min \{-\unicode[STIX]{x1D6FC}(w_{y_{i}})\}_{i=1,\ldots ,l}$
. Then
$r:=1/2\min \{-\unicode[STIX]{x1D6FC}(w_{y_{i}})\}_{i=1,\ldots ,l}$
. Then
 $r\in (0,1)$
and
$r\in (0,1)$
and
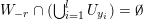 $W_{-r}\cap (\bigcup _{i=1}^{l}U_{y_{i}})=\emptyset$
. It follows that there exists
$W_{-r}\cap (\bigcup _{i=1}^{l}U_{y_{i}})=\emptyset$
. It follows that there exists
![]() $t>0$
such that
$t>0$
such that
![]() $\unicode[STIX]{x1D703}^{\ast }\geqslant t$
on
$\unicode[STIX]{x1D703}^{\ast }\geqslant t$
on
![]() $W_{-r}$
. By [Reference XieXie15a, Proposition 11.6], there exists
$W_{-r}$
. By [Reference XieXie15a, Proposition 11.6], there exists
![]() $N\geqslant 0$
such that
$N\geqslant 0$
such that
 $f_{\bullet }^{N}(W_{-r})\subseteq U_{E}$
. Then we have
$f_{\bullet }^{N}(W_{-r})\subseteq U_{E}$
. Then we have
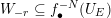 $W_{-r}\subseteq f_{\bullet }^{-N}(U_{E})$
.
$W_{-r}\subseteq f_{\bullet }^{-N}(U_{E})$
.
Since the boundary
 $\unicode[STIX]{x2202}(V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E})))$
of
$\unicode[STIX]{x2202}(V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E})))$
of
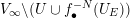 $V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E}))$
is finite and
$V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E}))$
is finite and
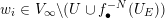 $w_{i}\in V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E}))$
for all
$w_{i}\in V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E}))$
for all
![]() $i\geqslant 1$
, we may suppose that there exists
$i\geqslant 1$
, we may suppose that there exists
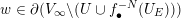 $w\in \unicode[STIX]{x2202}(V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E})))$
satisfying
$w\in \unicode[STIX]{x2202}(V_{\infty }\setminus (U\cup f_{\bullet }^{-N}(U_{E})))$
satisfying
![]() $w_{i}>w$
for all
$w_{i}>w$
for all
![]() $i\geqslant 1$
.
$i\geqslant 1$
.
Pick
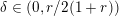 $\unicode[STIX]{x1D6FF}\in (0,r/2(1+r))$
. If, for all
$\unicode[STIX]{x1D6FF}\in (0,r/2(1+r))$
. If, for all
![]() $i\geqslant 1$
, we have
$i\geqslant 1$
, we have
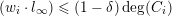 $(w_{i}\cdot l_{\infty })\leqslant (1-\unicode[STIX]{x1D6FF})\operatorname{deg}(C_{i})$
, then
$(w_{i}\cdot l_{\infty })\leqslant (1-\unicode[STIX]{x1D6FF})\operatorname{deg}(C_{i})$
, then
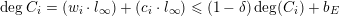 $\operatorname{deg}C_{i}=(w_{i}\cdot l_{\infty })+(c_{i}\cdot l_{\infty })\leqslant (1-\unicode[STIX]{x1D6FF})\operatorname{deg}(C_{i})+b_{E}$
. It follows that
$\operatorname{deg}C_{i}=(w_{i}\cdot l_{\infty })+(c_{i}\cdot l_{\infty })\leqslant (1-\unicode[STIX]{x1D6FF})\operatorname{deg}(C_{i})+b_{E}$
. It follows that
 $\operatorname{deg}(C_{i})\leqslant b_{E}/\unicode[STIX]{x1D6FF}$
.
$\operatorname{deg}(C_{i})\leqslant b_{E}/\unicode[STIX]{x1D6FF}$
.
Thus, we may suppose that
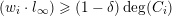 $(w_{i}\cdot l_{\infty })\geqslant (1-\unicode[STIX]{x1D6FF})\operatorname{deg}(C_{i})$
for all
$(w_{i}\cdot l_{\infty })\geqslant (1-\unicode[STIX]{x1D6FF})\operatorname{deg}(C_{i})$
for all
![]() $i\geqslant 1$
. For any
$i\geqslant 1$
. For any
![]() $i\neq j$
, we have
$i\neq j$
, we have
 $$\begin{eqnarray}\displaystyle \operatorname{deg}(C_{i})\operatorname{deg}(C_{j})\geqslant (c_{i}\cdot c_{j})+(w_{i}\cdot w_{j}) & {\geqslant} & \displaystyle b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))+(w_{i}\cdot l_{\infty })(w_{j}\cdot l_{\infty })(1-\unicode[STIX]{x1D6FC}(w))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))+(1-\unicode[STIX]{x1D6FF})^{2}(1+r)\operatorname{deg}(C_{i})\operatorname{deg}(C_{j}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{deg}(C_{i})\operatorname{deg}(C_{j})\geqslant (c_{i}\cdot c_{j})+(w_{i}\cdot w_{j}) & {\geqslant} & \displaystyle b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))+(w_{i}\cdot l_{\infty })(w_{j}\cdot l_{\infty })(1-\unicode[STIX]{x1D6FC}(w))\nonumber\\ \displaystyle & {\geqslant} & \displaystyle b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))+(1-\unicode[STIX]{x1D6FF})^{2}(1+r)\operatorname{deg}(C_{i})\operatorname{deg}(C_{j}).\nonumber\end{eqnarray}$$
Set
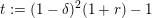 $t:=(1-\unicode[STIX]{x1D6FF})^{2}(1+r)-1$
; then we have
$t:=(1-\unicode[STIX]{x1D6FF})^{2}(1+r)-1$
; then we have
 $$\begin{eqnarray}t>(1-2\unicode[STIX]{x1D6FF})(1+r)-1>(1-r/(1+r))(1+r)-1=0\end{eqnarray}$$
$$\begin{eqnarray}t>(1-2\unicode[STIX]{x1D6FF})(1+r)-1>(1-r/(1+r))(1+r)-1=0\end{eqnarray}$$
and hence
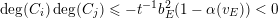 $\operatorname{deg}(C_{i})\operatorname{deg}(C_{j})\leqslant -t^{-1}b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))<0$
, which is a contradiction. This concludes the proof.◻
$\operatorname{deg}(C_{i})\operatorname{deg}(C_{j})\leqslant -t^{-1}b_{E}^{2}(1-\unicode[STIX]{x1D6FC}(v_{E}))<0$
, which is a contradiction. This concludes the proof.◻
Acknowledgements
Part of this work was done during the PhD study of the author with Charles Favre at École Polytechnique. I would like to thank Charles Favre for his constant support during this time. The referee carefully read a first version of this paper and his/her comments greatly improved it. I also thank Serge Cantat and Stéphane Lamy for useful discussions. I thank Vladimir Popov and Dragos Ghioca for their comments on the first version of the paper. I finally thank Matteo Ruggiero for answering my question about the theorem of Hadamard–Perron [Reference AbateAba01, Theorem 3.1.4].