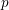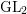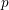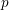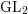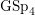1 Introduction
Drawing inspiration from earlier work of Hida and Lang, the paper [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] studied the image of the Galois representations associated with
![]() $p$
-adic families of modular forms, more precisely eigenforms of finite slope for the action of a Hecke algebra unramified outside of a fixed tame level. Such a family is defined by equipping a local piece of the eigencurve of the given tame level with an integral structure. A result of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] states that the Galois representation attached to a family has big image in the following sense: there is a ring
$p$
-adic families of modular forms, more precisely eigenforms of finite slope for the action of a Hecke algebra unramified outside of a fixed tame level. Such a family is defined by equipping a local piece of the eigencurve of the given tame level with an integral structure. A result of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] states that the Galois representation attached to a family has big image in the following sense: there is a ring
![]() $\mathbb{B}$
and a Lie subalgebra
$\mathbb{B}$
and a Lie subalgebra
![]() $\mathfrak{G}$
of
$\mathfrak{G}$
of
![]() $\mathfrak{g}\mathfrak{l}_{2}(\mathbb{B})$
attached to
$\mathfrak{g}\mathfrak{l}_{2}(\mathbb{B})$
attached to
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}$
, in a meaningful way, such that
$\operatorname{Im}\unicode[STIX]{x1D70C}$
, in a meaningful way, such that
![]() $\mathfrak{G}$
contains
$\mathfrak{G}$
contains
![]() $\mathfrak{l}\cdot \mathfrak{s}\mathfrak{l}_{2}(\mathbb{B})$
for a non-zero ideal
$\mathfrak{l}\cdot \mathfrak{s}\mathfrak{l}_{2}(\mathbb{B})$
for a non-zero ideal
![]() $\mathfrak{l}$
of
$\mathfrak{l}$
of
![]() $\mathbb{B}$
. This can be seen as an analogue, for a
$\mathbb{B}$
. This can be seen as an analogue, for a
![]() $p$
-adic family, of a classical result of Ribet and Momose on the image of the
$p$
-adic family, of a classical result of Ribet and Momose on the image of the
![]() $p$
-adic Galois representation attached to a classical eigenform [Reference RibetRib75, Reference MomoseMom81]. We call the Galois level of the family the largest ideal
$p$
-adic Galois representation attached to a classical eigenform [Reference RibetRib75, Reference MomoseMom81]. We call the Galois level of the family the largest ideal
![]() $\mathfrak{l}$
with the above property. The arguments in [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] rely heavily on the work of Hida and Lang for ordinary families [Reference HidaHid15, Reference LangLan16], in particular on the study by Lang of the conjugate self-twists of the Galois representations attached to families. A new ingredient in the positive slope case is relative Sen theory, that replaces ordinarity in some crucial steps. Another result of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] is an automorphic description of the Galois level of a family: the geometric points of its zero locus are the
$\mathfrak{l}$
with the above property. The arguments in [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] rely heavily on the work of Hida and Lang for ordinary families [Reference HidaHid15, Reference LangLan16], in particular on the study by Lang of the conjugate self-twists of the Galois representations attached to families. A new ingredient in the positive slope case is relative Sen theory, that replaces ordinarity in some crucial steps. Another result of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] is an automorphic description of the Galois level of a family: the geometric points of its zero locus are the
![]() $p$
-adic CM points of the family. This is also a generalization of a theorem of Hida in the ordinary case. The proof goes via the comparison of the Galois level with a fortuitous congruence ideal, that encodes the information on the CM specializations of the family. We call this ideal ‘fortuitous’ because, in contrast to what happens in the ordinary case, the CM specializations of a non-CM family do not correspond to congruences with CM families, that do not exist when the slope is positive.
$p$
-adic CM points of the family. This is also a generalization of a theorem of Hida in the ordinary case. The proof goes via the comparison of the Galois level with a fortuitous congruence ideal, that encodes the information on the CM specializations of the family. We call this ideal ‘fortuitous’ because, in contrast to what happens in the ordinary case, the CM specializations of a non-CM family do not correspond to congruences with CM families, that do not exist when the slope is positive.
In this paper we find analogous results for
![]() $p$
-adic families of Siegel modular forms of genus
$p$
-adic families of Siegel modular forms of genus
![]() $2$
and finite slope. We think that our work in this setting shows that the big image properties of Galois representations and their relations to congruences are part of a picture that can be extended to more general reductive groups. We remark that Hida and Tilouine already have some results for ordinary
$2$
and finite slope. We think that our work in this setting shows that the big image properties of Galois representations and their relations to congruences are part of a picture that can be extended to more general reductive groups. We remark that Hida and Tilouine already have some results for ordinary
![]() $p$
-adic families of
$p$
-adic families of
![]() $\operatorname{GSp}_{4}$
-eigenforms that are residually of ‘twisted Yoshida type’ [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15]. Their arguments rely on the Galois ordinarity of the families and on
$\operatorname{GSp}_{4}$
-eigenforms that are residually of ‘twisted Yoshida type’ [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15]. Their arguments rely on the Galois ordinarity of the families and on
![]() $R=T$
results, both of which are not available when the slope is positive. They obtain congruences between families that are lifts from
$R=T$
results, both of which are not available when the slope is positive. They obtain congruences between families that are lifts from
![]() $\operatorname{GL}_{2/F}$
, for a quadratic field
$\operatorname{GL}_{2/F}$
, for a quadratic field
![]() $F$
, and families that are not; their congruence ideals are then traditional and not fortuitous. In light of the results of the present paper, we think that fortuitous congruences should be regarded as general phenomena, that appear whenever we consider families of eigenforms for a reductive group that arise as
$F$
, and families that are not; their congruence ideals are then traditional and not fortuitous. In light of the results of the present paper, we think that fortuitous congruences should be regarded as general phenomena, that appear whenever we consider families of eigenforms for a reductive group that arise as
![]() $p$
-adic Langlands lifts from a group of smaller rank.
$p$
-adic Langlands lifts from a group of smaller rank.
The paper can be divided in two parts. In the first part (§§1–8), we define two-parameter families of
![]() $\operatorname{GSp}_{4}$
-eigenforms of finite slope and we attach Galois representations to them; we then prove that the image of these representations is big in a Lie theoretic sense, assuming that the residual representation is either of full image or a symmetric cube. In the second part (§§9–11), we prove that the size of the Galois representation attached to a two-parameter family is related to the congruences of the family with lifts of eigenforms for a smaller group, constructed via a
$\operatorname{GSp}_{4}$
-eigenforms of finite slope and we attach Galois representations to them; we then prove that the image of these representations is big in a Lie theoretic sense, assuming that the residual representation is either of full image or a symmetric cube. In the second part (§§9–11), we prove that the size of the Galois representation attached to a two-parameter family is related to the congruences of the family with lifts of eigenforms for a smaller group, constructed via a
![]() $p$
-adic Langlands transfer. In the first half, we need to solve many technical problems when passing from genus
$p$
-adic Langlands transfer. In the first half, we need to solve many technical problems when passing from genus
![]() $1$
to genus
$1$
to genus
![]() $2$
, whereas the second half is substantially different from its genus
$2$
, whereas the second half is substantially different from its genus
![]() $1$
counterpart. We present our results and arguments in more detail in the following.
$1$
counterpart. We present our results and arguments in more detail in the following.
Fix a prime
![]() $p$
and an integer
$p$
and an integer
![]() $M$
not divisible by
$M$
not divisible by
![]() $p$
. Let
$p$
. Let
![]() ${\mathcal{H}}_{2}^{M}$
be an abstract Hecke algebra unramified outside
${\mathcal{H}}_{2}^{M}$
be an abstract Hecke algebra unramified outside
![]() $Mp$
and of Iwahoric level at
$Mp$
and of Iwahoric level at
![]() $p$
. In their paper [Reference Andreatta, Iovita and PilloniAIP15], Andreatta, Iovita and Pilloni constructed a rigid analytic object
$p$
. In their paper [Reference Andreatta, Iovita and PilloniAIP15], Andreatta, Iovita and Pilloni constructed a rigid analytic object
![]() ${\mathcal{D}}_{2}$
, that we call the
${\mathcal{D}}_{2}$
, that we call the
![]() $\operatorname{GSp}_{4}$
-eigenvariety, and a map from
$\operatorname{GSp}_{4}$
-eigenvariety, and a map from
![]() ${\mathcal{H}}_{2}^{M}$
to the ring of analytic functions on
${\mathcal{H}}_{2}^{M}$
to the ring of analytic functions on
![]() ${\mathcal{D}}_{2}$
, interpolating the systems of Hecke eigenvalues associated with the
${\mathcal{D}}_{2}$
, interpolating the systems of Hecke eigenvalues associated with the
![]() $p$
-stabilized Siegel modular forms of genus
$p$
-stabilized Siegel modular forms of genus
![]() $2$
and tame level
$2$
and tame level
![]() $M$
. The eigenvariety
$M$
. The eigenvariety
![]() ${\mathcal{D}}_{2}$
is equipped with a map to the two-dimensional weight space
${\mathcal{D}}_{2}$
is equipped with a map to the two-dimensional weight space
![]() ${\mathcal{W}}_{2}$
, that is the rigid analytic space associated with the formal scheme
${\mathcal{W}}_{2}$
, that is the rigid analytic space associated with the formal scheme
![]() $\operatorname{Spf}\mathbb{Z}_{p}[[(\mathbb{Z}_{p}^{\times })^{2}]]$
by Berthelot’s construction [Reference de JongdeJ95, §7]. For our purposes, it is important that families be defined integrally, so we cannot work globally on irreducible components of the eigenvariety. We consider instead an admissible domain
$\operatorname{Spf}\mathbb{Z}_{p}[[(\mathbb{Z}_{p}^{\times })^{2}]]$
by Berthelot’s construction [Reference de JongdeJ95, §7]. For our purposes, it is important that families be defined integrally, so we cannot work globally on irreducible components of the eigenvariety. We consider instead an admissible domain
![]() $D_{h}$
on
$D_{h}$
on
![]() ${\mathcal{D}}_{2}$
consisting of the points of slope bounded by a rational number
${\mathcal{D}}_{2}$
consisting of the points of slope bounded by a rational number
![]() $h$
and of weight in a wide open disc in the weight space. If the radius of this disc is sufficiently small with respect to
$h$
and of weight in a wide open disc in the weight space. If the radius of this disc is sufficiently small with respect to
![]() $h$
, the restriction of the weight map to
$h$
, the restriction of the weight map to
![]() $D_{h}$
is a finite map thanks to a result of Bellaïche (Proposition 4.1). A suitably chosen integral structure on the weight disc induces an integral structure on
$D_{h}$
is a finite map thanks to a result of Bellaïche (Proposition 4.1). A suitably chosen integral structure on the weight disc induces an integral structure on
![]() $D_{h}$
. This means that we can define a local profinite ring
$D_{h}$
. This means that we can define a local profinite ring
![]() $\mathbb{I}^{\circ }$
and a map
$\mathbb{I}^{\circ }$
and a map
![]() ${\mathcal{H}}_{2}^{M}\rightarrow \mathbb{I}^{\circ }$
that interpolates the systems of Hecke eigenvalues of the classical eigenforms appearing in
${\mathcal{H}}_{2}^{M}\rightarrow \mathbb{I}^{\circ }$
that interpolates the systems of Hecke eigenvalues of the classical eigenforms appearing in
![]() $D_{h}$
. An argument by Chenevier gives a Galois pseudocharacter on
$D_{h}$
. An argument by Chenevier gives a Galois pseudocharacter on
![]() $D_{h}$
, that we lift to a representation
$D_{h}$
, that we lift to a representation
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}^{\circ })$
(Lemma 4.7). We define the ‘conjugate self-twists’ of
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}^{\circ })$
(Lemma 4.7). We define the ‘conjugate self-twists’ of
![]() $\unicode[STIX]{x1D70C}$
as automorphisms of
$\unicode[STIX]{x1D70C}$
as automorphisms of
![]() $\mathbb{I}^{\circ }$
that induce an isomorphism of
$\mathbb{I}^{\circ }$
that induce an isomorphism of
![]() $\unicode[STIX]{x1D70C}$
with one of its twists by a Dirichlet character (Definition 5.1). We write
$\unicode[STIX]{x1D70C}$
with one of its twists by a Dirichlet character (Definition 5.1). We write
![]() $\mathbb{I}_{0}^{\circ }$
for the subring of elements of
$\mathbb{I}_{0}^{\circ }$
for the subring of elements of
![]() $\mathbb{I}^{\circ }$
fixed by all the conjugate self-twists. We define a certain completion
$\mathbb{I}^{\circ }$
fixed by all the conjugate self-twists. We define a certain completion
![]() $\mathbb{B}$
of
$\mathbb{B}$
of
![]() $\mathbb{I}_{0}^{\circ }[1/p]$
and a Lie subalgebra
$\mathbb{I}_{0}^{\circ }[1/p]$
and a Lie subalgebra
![]() $\operatorname{Lie}(\operatorname{Im}\unicode[STIX]{x1D70C})$
of
$\operatorname{Lie}(\operatorname{Im}\unicode[STIX]{x1D70C})$
of
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B})$
attached to
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B})$
attached to
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}$
(see §7.1). We assume that
$\operatorname{Im}\unicode[STIX]{x1D70C}$
(see §7.1). We assume that
![]() $\unicode[STIX]{x1D70C}$
is
$\unicode[STIX]{x1D70C}$
is
![]() $\mathbb{Z}_{p}$
-regular (Definition 3.10) and that the residual representation
$\mathbb{Z}_{p}$
-regular (Definition 3.10) and that the residual representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
is either full or of symmetric cube type (Definition 3.11). Our first main result is the following.
$\overline{\unicode[STIX]{x1D70C}}$
is either full or of symmetric cube type (Definition 3.11). Our first main result is the following.
Theorem 1.1 (Theorem 8.1).
There exists a non-zero ideal
![]() $\mathfrak{l}$
of
$\mathfrak{l}$
of
![]() $\mathbb{B}$
such that
$\mathbb{B}$
such that
![]() $\mathfrak{l}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B})\subset \operatorname{Lie}(\operatorname{Im}\unicode[STIX]{x1D70C})$
.
$\mathfrak{l}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B})\subset \operatorname{Lie}(\operatorname{Im}\unicode[STIX]{x1D70C})$
.
We call the Galois level of the family the largest ideal
![]() $\mathfrak{l}$
satisfying the inclusion of Theorem 1.1. We give here a summary of the proof of Theorem 1.1. We first show that, under our assumptions on
$\mathfrak{l}$
satisfying the inclusion of Theorem 1.1. We give here a summary of the proof of Theorem 1.1. We first show that, under our assumptions on
![]() $\overline{\unicode[STIX]{x1D70C}}$
, there exists a classical weight such that
$\overline{\unicode[STIX]{x1D70C}}$
, there exists a classical weight such that
![]() $\unicode[STIX]{x1D70C}$
specializes to a representation with big image at all points of this weight appearing on the family (Theorem 3.12). Here we need the recent classicality result contained in [Reference Bijakowski, Pilloni and StrohBPS16, Theorem 5.3.1]. Another essential ingredient is a result of Pink (Theorem 3.13) that we use to show that the representation associated with a
$\unicode[STIX]{x1D70C}$
specializes to a representation with big image at all points of this weight appearing on the family (Theorem 3.12). Here we need the recent classicality result contained in [Reference Bijakowski, Pilloni and StrohBPS16, Theorem 5.3.1]. Another essential ingredient is a result of Pink (Theorem 3.13) that we use to show that the representation associated with a
![]() $\operatorname{GSp}_{4}$
-eigenform that is not a lift from a smaller group has big image with respect to the ring fixed by its conjugate self-twists. This is an analogue of the result of Ribet and Momose for
$\operatorname{GSp}_{4}$
-eigenform that is not a lift from a smaller group has big image with respect to the ring fixed by its conjugate self-twists. This is an analogue of the result of Ribet and Momose for
![]() $\operatorname{GL}_{2}$
-eigenforms. We prove some results that are needed in the second part of the paper (in the proof of Theorem 1.2) and that yield as a corollary the fact that a form which is not a lift satisfies the assumptions of Pink’s theorem (Corollary 3.9).
$\operatorname{GL}_{2}$
-eigenforms. We prove some results that are needed in the second part of the paper (in the proof of Theorem 1.2) and that yield as a corollary the fact that a form which is not a lift satisfies the assumptions of Pink’s theorem (Corollary 3.9).
Once a classical weight with the desired properties is chosen, we follow a strategy of Lang to obtain some information on the image of
![]() $\unicode[STIX]{x1D70C}$
. As a first step we need to show that a big image result holds for the product of the specializations of
$\unicode[STIX]{x1D70C}$
. As a first step we need to show that a big image result holds for the product of the specializations of
![]() $\unicode[STIX]{x1D70C}$
of a given weight, rather than just for a single one (Proposition 6.10). The argument here relies on Goursat’s lemma and on the classification of subnormal subgroups of symplectic groups by Tazhetdinov. Afterwards, we use the result of the first step to construct some non-trivial unipotent elements in the image of
$\unicode[STIX]{x1D70C}$
of a given weight, rather than just for a single one (Proposition 6.10). The argument here relies on Goursat’s lemma and on the classification of subnormal subgroups of symplectic groups by Tazhetdinov. Afterwards, we use the result of the first step to construct some non-trivial unipotent elements in the image of
![]() $\unicode[STIX]{x1D70C}$
. To do this, we need to prove an analogue of [Reference LangLan16, Theorem 3.1] that allows us to lift the conjugate self-twists of the specializations of
$\unicode[STIX]{x1D70C}$
. To do this, we need to prove an analogue of [Reference LangLan16, Theorem 3.1] that allows us to lift the conjugate self-twists of the specializations of
![]() $\unicode[STIX]{x1D70C}$
at our chosen weight to conjugate self-twists of
$\unicode[STIX]{x1D70C}$
at our chosen weight to conjugate self-twists of
![]() $\unicode[STIX]{x1D70C}$
itself. The arguments of Lang about the lifting of the conjugate self-twists to automorphisms of a suitable deformation ring can be translated into the genus
$\unicode[STIX]{x1D70C}$
itself. The arguments of Lang about the lifting of the conjugate self-twists to automorphisms of a suitable deformation ring can be translated into the genus
![]() $2$
case with little effort, but descending to a conjugate self-twist of the family requires some specific ingredients. Precisely, we prove that we can twist a family of
$2$
case with little effort, but descending to a conjugate self-twist of the family requires some specific ingredients. Precisely, we prove that we can twist a family of
![]() $\operatorname{GSp}_{4}$
-eigenforms by a Dirichlet character to obtain a new family (Lemma 5.8) and we rely on the étaleness of the eigenvariety above our chosen weight.
$\operatorname{GSp}_{4}$
-eigenforms by a Dirichlet character to obtain a new family (Lemma 5.8) and we rely on the étaleness of the eigenvariety above our chosen weight.
In §7, we show how the relative Sen theory of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, §5] can be extended to the group
![]() $\operatorname{GSp}_{4}$
, to associate a Sen operator with
$\operatorname{GSp}_{4}$
, to associate a Sen operator with
![]() $\unicode[STIX]{x1D70C}$
. The eigenvalues of this operator are given explicitly by the interpolation of the Hodge–Tate weights of the classical specializations of the family (Proposition 7.12). The exponential of the Sen operator induces by conjugation a structure of
$\unicode[STIX]{x1D70C}$
. The eigenvalues of this operator are given explicitly by the interpolation of the Hodge–Tate weights of the classical specializations of the family (Proposition 7.12). The exponential of the Sen operator induces by conjugation a structure of
![]() $\mathbb{Z}_{p}[[T_{1},T_{2}]]$
-Lie algebra on
$\mathbb{Z}_{p}[[T_{1},T_{2}]]$
-Lie algebra on
![]() $\operatorname{Lie}(\operatorname{Im}\unicode[STIX]{x1D70C})$
, so that the special elements we constructed generate a non-trivial congruence subalgebra. This proves Theorem 1.1.
$\operatorname{Lie}(\operatorname{Im}\unicode[STIX]{x1D70C})$
, so that the special elements we constructed generate a non-trivial congruence subalgebra. This proves Theorem 1.1.
When
![]() $\overline{\unicode[STIX]{x1D70C}}$
has full image, the Galois level of the family is trivial (Corollary 11.5), so the main focus of the rest of the paper is the case where
$\overline{\unicode[STIX]{x1D70C}}$
has full image, the Galois level of the family is trivial (Corollary 11.5), so the main focus of the rest of the paper is the case where
![]() $\overline{\unicode[STIX]{x1D70C}}$
is a symmetric cube. We can give two definitions of a symmetric cube locus on the eigenvariety: an automorphic definition, as the locus of points whose system of Hecke eigenvalues is obtained from that of an overconvergent
$\overline{\unicode[STIX]{x1D70C}}$
is a symmetric cube. We can give two definitions of a symmetric cube locus on the eigenvariety: an automorphic definition, as the locus of points whose system of Hecke eigenvalues is obtained from that of an overconvergent
![]() $\operatorname{GL}_{2}$
-eigenform via a symmetric cube morphism of Hecke algebras; and a Galois definition, as the locus of points whose Galois representation is the symmetric cube of that associated with an overconvergent
$\operatorname{GL}_{2}$
-eigenform via a symmetric cube morphism of Hecke algebras; and a Galois definition, as the locus of points whose Galois representation is the symmetric cube of that associated with an overconvergent
![]() $\operatorname{GL}_{2}$
-eigenform. An important result is the following.
$\operatorname{GL}_{2}$
-eigenform. An important result is the following.
Theorem 1.2 (Theorem 10.1).
The automorphic and Galois definitions of the symmetric cube locus are equivalent.
Theorem 1.2 plays an essential role in describing the Galois level of the family by automorphic means. Note that this result and its role in our work are completely new with respect to the genus
![]() $1$
case: there the only possible congruences are of CM type and it is trivial to see that a point of small Galois image, contained in the normalizer of a torus, is a
$1$
case: there the only possible congruences are of CM type and it is trivial to see that a point of small Galois image, contained in the normalizer of a torus, is a
![]() $p$
-adic CM point (see [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Remark 3.11]).
$p$
-adic CM point (see [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Remark 3.11]).
The proof of Theorem 1.2 goes via the theory of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules. It is known from the work of Kisin and Emerton that a two-dimensional
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules. It is known from the work of Kisin and Emerton that a two-dimensional
![]() $p$
-adic representation of
$p$
-adic representation of
![]() $G_{\mathbb{Q}}$
is associated with an overconvergent
$G_{\mathbb{Q}}$
is associated with an overconvergent
![]() $\operatorname{GL}_{2}$
-eigenform, up to a twist, if and only if it is trianguline. Thanks to the recent work of Kedlaya, Pottharst and Xiao on triangulations over eigenvarieties, we know that the ‘only if’ part also holds for overconvergent
$\operatorname{GL}_{2}$
-eigenform, up to a twist, if and only if it is trianguline. Thanks to the recent work of Kedlaya, Pottharst and Xiao on triangulations over eigenvarieties, we know that the ‘only if’ part also holds for overconvergent
![]() $\operatorname{GSp}_{4}$
-eigenforms (Theorem 3.2). We combine their results with some arguments of Di Matteo [Reference Di MatteoDiM13b] that relate the triangulinity of a representation to that of its symmetric cube, giving the desired result. As a corollary we deduce that if a
$\operatorname{GSp}_{4}$
-eigenforms (Theorem 3.2). We combine their results with some arguments of Di Matteo [Reference Di MatteoDiM13b] that relate the triangulinity of a representation to that of its symmetric cube, giving the desired result. As a corollary we deduce that if a
![]() $p$
-old point of symmetric cube type of
$p$
-old point of symmetric cube type of
![]() ${\mathcal{D}}_{2}^{M}$
is classical, then it is obtained from a classical point of an eigencurve for
${\mathcal{D}}_{2}^{M}$
is classical, then it is obtained from a classical point of an eigencurve for
![]() $\operatorname{GL}_{2}$
, via the classical Langlands lift attached to the symmetric cube representation by Kim and Shahidi [Reference Kim and ShahidiKS02].
$\operatorname{GL}_{2}$
, via the classical Langlands lift attached to the symmetric cube representation by Kim and Shahidi [Reference Kim and ShahidiKS02].
We study further the symmetric cube locus and show that it is Zariski-closed with zero- and one-dimensional irreducible components. The one-dimensional part of the locus can be constructed as the image of a morphism from an eigencurve for
![]() $\operatorname{GL}_{2}$
, of a suitable tame level, to
$\operatorname{GL}_{2}$
, of a suitable tame level, to
![]() ${\mathcal{D}}_{2}^{M}$
. This morphism is obtained by interpolating
${\mathcal{D}}_{2}^{M}$
. This morphism is obtained by interpolating
![]() $p$
-adically the classical symmetric cube Langlands lift, via an argument that goes back to Chenevier’s work on the
$p$
-adically the classical symmetric cube Langlands lift, via an argument that goes back to Chenevier’s work on the
![]() $p$
-adic Jacquet–Langlands correspondence [Reference ChenevierChe05] and is now quite standard. We assume the existence of this morphism (Proposition 9.11) and refer to [Reference ContiCon16, §§3.6–3.9] for a construction of the morphism that relies on the results of [Reference Bellaïche and ChenevierBC09, §7.2.3].
$p$
-adic Jacquet–Langlands correspondence [Reference ChenevierChe05] and is now quite standard. We assume the existence of this morphism (Proposition 9.11) and refer to [Reference ContiCon16, §§3.6–3.9] for a construction of the morphism that relies on the results of [Reference Bellaïche and ChenevierBC09, §7.2.3].
The zero-dimensional components of the symmetric cube locus are given by isolated
![]() $p$
-adic Langlands lifts, that cannot be interpolated owing to the fact that their slopes do not vary analytically. The appearance of such points is related to the existence of more than one crystalline period for the corresponding Galois representation (Proposition 3.4).
$p$
-adic Langlands lifts, that cannot be interpolated owing to the fact that their slopes do not vary analytically. The appearance of such points is related to the existence of more than one crystalline period for the corresponding Galois representation (Proposition 3.4).
Restricting once again our attention to a local piece of the eigencurve describing a family, we define a symmetric cube congruence ideal that measures the locus of symmetric cube specializations of the family (Definition 11.1). We call it a fortuitous congruence ideal: since there are no two-parameter families of symmetric cube type, the congruences detected by this ideal are symmetric cube specializations of a family that is not globally a symmetric cube. Thanks to Theorem 1.2, that serves as a bridge between the automorphic and Galois sides, we can relate the congruence ideal with the Galois level of the family.
Theorem 1.3 (Theorem 11.4).
The sets of prime divisors of the Galois level and of the symmetric cube congruence ideal coincide outside of a finite and explicit bad locus.
We think that the results of this paper can be generalized by allowing for different residual representations, hence different types of congruences, or by replacing
![]() $\operatorname{GSp}_{4}$
by other reductive groups for which an eigenvariety has been constructed. We hope to come back to this problem in a later work.
$\operatorname{GSp}_{4}$
by other reductive groups for which an eigenvariety has been constructed. We hope to come back to this problem in a later work.
Notation.
We fix some notation and conventions. In the text,
![]() $p$
will always denote a prime number strictly larger than three. Most arguments work for every odd
$p$
will always denote a prime number strictly larger than three. Most arguments work for every odd
![]() $p$
; we specify when this is not sufficient. We choose algebraic closures
$p$
; we specify when this is not sufficient. We choose algebraic closures
![]() $\overline{\mathbb{Q}}$
and
$\overline{\mathbb{Q}}$
and
![]() $\overline{\mathbb{Q}}_{p}$
of
$\overline{\mathbb{Q}}_{p}$
of
![]() $\mathbb{Q}$
and
$\mathbb{Q}$
and
![]() $\mathbb{Q}_{p}$
, respectively. If
$\mathbb{Q}_{p}$
, respectively. If
![]() $K$
is a finite extension of
$K$
is a finite extension of
![]() $\mathbb{Q}$
or
$\mathbb{Q}$
or
![]() $\mathbb{Q}_{p}$
, we denote by
$\mathbb{Q}_{p}$
, we denote by
![]() $G_{K}$
its absolute Galois group. We equip
$G_{K}$
its absolute Galois group. We equip
![]() $G_{K}$
with its profinite topology. We denote by
$G_{K}$
with its profinite topology. We denote by
![]() ${\mathcal{O}}_{K}$
the ring of integers of
${\mathcal{O}}_{K}$
the ring of integers of
![]() $K$
. If
$K$
. If
![]() $K$
is local, we denote by
$K$
is local, we denote by
![]() $\mathfrak{m}_{K}$
the maximal ideal of
$\mathfrak{m}_{K}$
the maximal ideal of
![]() ${\mathcal{O}}_{K}$
. For every prime
${\mathcal{O}}_{K}$
. For every prime
![]() $p$
, we fix an embedding
$p$
, we fix an embedding
![]() $\unicode[STIX]{x1D704}_{p}:\overline{\mathbb{Q}}{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
, identifying
$\unicode[STIX]{x1D704}_{p}:\overline{\mathbb{Q}}{\hookrightarrow}\overline{\mathbb{Q}}_{p}$
, identifying
![]() $G_{\mathbb{Q}_{p}}$
with a decomposition group of
$G_{\mathbb{Q}_{p}}$
with a decomposition group of
![]() $G_{\mathbb{Q}}$
. We fix a valuation
$G_{\mathbb{Q}}$
. We fix a valuation
![]() $v_{p}$
on
$v_{p}$
on
![]() $\overline{\mathbb{Q}}_{p}$
normalized so that
$\overline{\mathbb{Q}}_{p}$
normalized so that
![]() $v_{p}(p)=1$
. It defines a norm given by
$v_{p}(p)=1$
. It defines a norm given by
![]() $|\,\cdot \,|=p^{-v_{p}(\cdot )}$
. We denote by
$|\,\cdot \,|=p^{-v_{p}(\cdot )}$
. We denote by
![]() $\mathbb{C}_{p}$
the completion of
$\mathbb{C}_{p}$
the completion of
![]() $\overline{\mathbb{Q}}_{p}$
with respect to this norm.
$\overline{\mathbb{Q}}_{p}$
with respect to this norm.
All rigid analytic spaces will be considered in the sense of Tate (see [Reference Bosch, Güntzer and RemmertBGR84, Part C]). Let
![]() $K/\mathbb{Q}_{p}$
be a field extension and let
$K/\mathbb{Q}_{p}$
be a field extension and let
![]() $X$
be a rigid analytic space over
$X$
be a rigid analytic space over
![]() $K$
. We denote by
$K$
. We denote by
![]() ${\mathcal{O}}(X)$
the
${\mathcal{O}}(X)$
the
![]() $K$
-algebra of rigid analytic functions on
$K$
-algebra of rigid analytic functions on
![]() $X$
, and by
$X$
, and by
![]() ${\mathcal{O}}(X)^{\circ }$
the
${\mathcal{O}}(X)^{\circ }$
the
![]() ${\mathcal{O}}_{K}$
-subalgebra of functions of norm bounded by
${\mathcal{O}}_{K}$
-subalgebra of functions of norm bounded by
![]() $1$
(we often say ‘functions bounded by 1’ meaning that they are bounded in norm). When
$1$
(we often say ‘functions bounded by 1’ meaning that they are bounded in norm). When
![]() $f:X\rightarrow Y$
is a map of rigid analytic spaces, we denote by
$f:X\rightarrow Y$
is a map of rigid analytic spaces, we denote by
![]() $f^{\ast }:{\mathcal{O}}(Y)\rightarrow {\mathcal{O}}(X)$
the map induced by
$f^{\ast }:{\mathcal{O}}(Y)\rightarrow {\mathcal{O}}(X)$
the map induced by
![]() $f$
. There is a Grothendieck topology on
$f$
. There is a Grothendieck topology on
![]() $X$
, called the Tate topology; we refer to [Reference Bosch, Güntzer and RemmertBGR84, Proposition 9.1.4/2] for the definition of its admissible open sets and admissible coverings. There is a notion of irreducible components for
$X$
, called the Tate topology; we refer to [Reference Bosch, Güntzer and RemmertBGR84, Proposition 9.1.4/2] for the definition of its admissible open sets and admissible coverings. There is a notion of irreducible components for
![]() $X$
; see [Reference ConradCon99] for the details. We say that
$X$
; see [Reference ConradCon99] for the details. We say that
![]() $X$
is equidimensional of dimension
$X$
is equidimensional of dimension
![]() $d$
if all its irreducible components have dimension
$d$
if all its irreducible components have dimension
![]() $d$
.
$d$
.
We say that
![]() $X$
is wide open if there exists an admissible covering
$X$
is wide open if there exists an admissible covering
![]() $\{X_{i}\}\text{}_{i\in \mathbb{N}}$
of
$\{X_{i}\}\text{}_{i\in \mathbb{N}}$
of
![]() $X$
by affinoid domains
$X$
by affinoid domains
![]() $X_{i}$
such that, for every
$X_{i}$
such that, for every
![]() $i$
,
$i$
,
![]() $X_{i}\subset X_{i+1}$
and the map
$X_{i}\subset X_{i+1}$
and the map
![]() ${\mathcal{O}}(X_{i+1})\rightarrow {\mathcal{O}}(X_{i})$
induced by the previous inclusion is compact.
${\mathcal{O}}(X_{i+1})\rightarrow {\mathcal{O}}(X_{i})$
induced by the previous inclusion is compact.
Let
![]() $S$
be any subset of
$S$
be any subset of
![]() $X(\mathbb{C}_{p})$
. We say that
$X(\mathbb{C}_{p})$
. We say that
![]() $S$
is:
$S$
is:
(i) a discrete subset of
 $X(\mathbb{C}_{p})$
if
$X(\mathbb{C}_{p})$
if
 $S\cap A$
is a finite set for any open affinoid
$S\cap A$
is a finite set for any open affinoid
 $A\subset X(\mathbb{C}_{p})$
;
$A\subset X(\mathbb{C}_{p})$
;(ii) a Zariski-dense subset of
 $X(\mathbb{C}_{p})$
if, for every
$X(\mathbb{C}_{p})$
if, for every
 $f\in {\mathcal{O}}(X)$
vanishing at every point of
$f\in {\mathcal{O}}(X)$
vanishing at every point of
 $S$
,
$S$
,
 $f$
is identically zero;
$f$
is identically zero;(iii) an accumulation subset of
 $X(\mathbb{C}_{p})$
if for every
$X(\mathbb{C}_{p})$
if for every
 $x\in S$
there exists a basis
$x\in S$
there exists a basis
 ${\mathcal{B}}$
of affinoid neighborhoods of
${\mathcal{B}}$
of affinoid neighborhoods of
 $x$
in
$x$
in
 $X$
such that for every
$X$
such that for every
 $A\in {\mathcal{B}}$
the set
$A\in {\mathcal{B}}$
the set
 $S\cap A(\mathbb{C}_{p})$
is Zariski-dense in
$S\cap A(\mathbb{C}_{p})$
is Zariski-dense in
 $A$
(this term is borrowed from [Reference Bellaïche and ChenevierBC09, §3.3.1]).
$A$
(this term is borrowed from [Reference Bellaïche and ChenevierBC09, §3.3.1]).
We denote by
![]() $\mathbb{A}^{d}$
the
$\mathbb{A}^{d}$
the
![]() $d$
-dimensional rigid analytic affine space over
$d$
-dimensional rigid analytic affine space over
![]() $\mathbb{Q}_{p}$
. Given a point
$\mathbb{Q}_{p}$
. Given a point
![]() $x\in \mathbb{A}^{d}(\mathbb{C}_{p})$
and
$x\in \mathbb{A}^{d}(\mathbb{C}_{p})$
and
![]() $r\in p^{\mathbb{Q}}$
, we denote by
$r\in p^{\mathbb{Q}}$
, we denote by
![]() $B_{d}(x,r)$
the
$B_{d}(x,r)$
the
![]() $d$
-dimensional closed disc of centre
$d$
-dimensional closed disc of centre
![]() $x$
and radius
$x$
and radius
![]() $r$
. It is an affinoid domain defined over
$r$
. It is an affinoid domain defined over
![]() $\mathbb{C}_{p}$
. We denote by
$\mathbb{C}_{p}$
. We denote by
![]() $B_{d}(x,r^{-})$
the
$B_{d}(x,r^{-})$
the
![]() $d$
-dimensional wide open disc of centre
$d$
-dimensional wide open disc of centre
![]() $x$
and radius
$x$
and radius
![]() $r$
, defined as the rigid analytic space over
$r$
, defined as the rigid analytic space over
![]() $\mathbb{C}_{p}$
given by the increasing union of the
$\mathbb{C}_{p}$
given by the increasing union of the
![]() $d$
-dimensional affinoid discs of centre
$d$
-dimensional affinoid discs of centre
![]() $x$
and radii
$x$
and radii
![]() $\{r_{i}\}\text{}_{i\in \mathbb{N}}$
with
$\{r_{i}\}\text{}_{i\in \mathbb{N}}$
with
![]() $r_{i}<r$
and
$r_{i}<r$
and
![]() $\lim _{i\mapsto +\infty }r_{i}=r$
.
$\lim _{i\mapsto +\infty }r_{i}=r$
.
For every
![]() $n\geqslant 1$
we denote by
$n\geqslant 1$
we denote by
![]() $\unicode[STIX]{x1D7D9}_{n}$
the
$\unicode[STIX]{x1D7D9}_{n}$
the
![]() $n\times n$
unit matrix. Let
$n\times n$
unit matrix. Let
![]() $g\geqslant 1$
be an integer and let
$g\geqslant 1$
be an integer and let
![]() $s$
be the
$s$
be the
![]() $g\times g$
antidiagonal unit matrix
$g\times g$
antidiagonal unit matrix
![]() $(\unicode[STIX]{x1D6FF}_{i,n-i}(i,j))_{1\leqslant i,j\leqslant g}$
. Let
$(\unicode[STIX]{x1D6FF}_{i,n-i}(i,j))_{1\leqslant i,j\leqslant g}$
. Let
![]() $J_{g}$
be the
$J_{g}$
be the
![]() $2g\times 2g$
matrix
$2g\times 2g$
matrix
![]() $(\!\begin{smallmatrix}0 & s\\ -s & 0\end{smallmatrix}\!)$
. We denote by
$(\!\begin{smallmatrix}0 & s\\ -s & 0\end{smallmatrix}\!)$
. We denote by
![]() $\operatorname{GSp}_{2g}$
the algebraic group of symplectic similitudes for
$\operatorname{GSp}_{2g}$
the algebraic group of symplectic similitudes for
![]() $J_{g}$
, defined over
$J_{g}$
, defined over
![]() $\mathbb{Z}$
; for every ring
$\mathbb{Z}$
; for every ring
![]() $R$
the
$R$
the
![]() $R$
-points of this group are given by
$R$
-points of this group are given by
The map
![]() $A\rightarrow \unicode[STIX]{x1D708}(A)$
defines a character
$A\rightarrow \unicode[STIX]{x1D708}(A)$
defines a character
![]() $\unicode[STIX]{x1D708}:\operatorname{GSp}_{4}(R)\rightarrow R^{\times }$
. We refer to
$\unicode[STIX]{x1D708}:\operatorname{GSp}_{4}(R)\rightarrow R^{\times }$
. We refer to
![]() $\unicode[STIX]{x1D708}$
as the similitude factor and we set
$\unicode[STIX]{x1D708}$
as the similitude factor and we set
![]() $\operatorname{Sp}_{2g}(R)=\{A\in \operatorname{GSp}_{2g}(R)\,|\,\unicode[STIX]{x1D708}(A)=1\}$
.
$\operatorname{Sp}_{2g}(R)=\{A\in \operatorname{GSp}_{2g}(R)\,|\,\unicode[STIX]{x1D708}(A)=1\}$
.
We denote by
![]() $B_{g}$
the Borel subgroup of
$B_{g}$
the Borel subgroup of
![]() $\operatorname{GSp}_{2g}$
such that for every ring
$\operatorname{GSp}_{2g}$
such that for every ring
![]() $R$
the
$R$
the
![]() $R$
-points of
$R$
-points of
![]() $B_{g}$
are the upper triangular matrices in
$B_{g}$
are the upper triangular matrices in
![]() $\operatorname{GSp}_{2g}(R)$
. We let
$\operatorname{GSp}_{2g}(R)$
. We let
![]() $T_{g}$
be the maximal torus such that for every ring
$T_{g}$
be the maximal torus such that for every ring
![]() $R$
the
$R$
the
![]() $R$
-points of
$R$
-points of
![]() $T_{g}$
are the diagonal matrices in
$T_{g}$
are the diagonal matrices in
![]() $\operatorname{GSp}_{2g}(R)$
. We write
$\operatorname{GSp}_{2g}(R)$
. We write
![]() $U_{g}$
for the unipotent radical of
$U_{g}$
for the unipotent radical of
![]() $B_{g}$
. We have
$B_{g}$
. We have
![]() $B_{g}=T_{g}U_{g}$
. We will always speak of weights and roots for
$B_{g}=T_{g}U_{g}$
. We will always speak of weights and roots for
![]() $\operatorname{GSp}_{2g}$
with respect to the previous choice of Borel subgroup and torus. For every root
$\operatorname{GSp}_{2g}$
with respect to the previous choice of Borel subgroup and torus. For every root
![]() $\unicode[STIX]{x1D6FC}$
, we denote by
$\unicode[STIX]{x1D6FC}$
, we denote by
![]() $U^{\unicode[STIX]{x1D6FC}}$
the corresponding one-parameter unipotent subgroup of
$U^{\unicode[STIX]{x1D6FC}}$
the corresponding one-parameter unipotent subgroup of
![]() $\operatorname{GSp}_{2g}$
. For every prime
$\operatorname{GSp}_{2g}$
. For every prime
![]() $\ell$
, we write
$\ell$
, we write
![]() $I_{g,\ell }$
for the Iwahori subgroup of
$I_{g,\ell }$
for the Iwahori subgroup of
![]() $\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell })$
corresponding to our choice of Borel subgroup, and we define some compact open subgroups of
$\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell })$
corresponding to our choice of Borel subgroup, and we define some compact open subgroups of
![]() $\operatorname{GSp}_{2g}(\mathbb{A}_{\mathbb{Q}})$
by:
$\operatorname{GSp}_{2g}(\mathbb{A}_{\mathbb{Q}})$
by:
(i)
 $\unicode[STIX]{x1D6E4}^{(g)}(\ell ^{n})=\{h\in \operatorname{GSp}_{2g}(\widehat{\mathbb{Z}})\,|\,h_{\ell }\cong \unicode[STIX]{x1D7D9}_{2g}\hspace{0.6em}({\rm mod}\hspace{0.2em}\ell ^{n})\}$
;
$\unicode[STIX]{x1D6E4}^{(g)}(\ell ^{n})=\{h\in \operatorname{GSp}_{2g}(\widehat{\mathbb{Z}})\,|\,h_{\ell }\cong \unicode[STIX]{x1D7D9}_{2g}\hspace{0.6em}({\rm mod}\hspace{0.2em}\ell ^{n})\}$
;(ii)
 $\unicode[STIX]{x1D6E4}_{1}^{(g)}(\ell ^{n})=\{h\in \operatorname{GSp}_{2g}(\widehat{\mathbb{Z}})\,|\,h_{\ell }\hspace{0.6em}({\rm mod}\hspace{0.2em}\ell ^{n})\in U_{g}(\mathbb{Z}/\ell ^{n}\mathbb{Z})\}$
;
$\unicode[STIX]{x1D6E4}_{1}^{(g)}(\ell ^{n})=\{h\in \operatorname{GSp}_{2g}(\widehat{\mathbb{Z}})\,|\,h_{\ell }\hspace{0.6em}({\rm mod}\hspace{0.2em}\ell ^{n})\in U_{g}(\mathbb{Z}/\ell ^{n}\mathbb{Z})\}$
;(iii)
 $\unicode[STIX]{x1D6E4}_{0}^{(g)}(\ell ^{n})=\{h\in \operatorname{GSp}_{2g}(\widehat{\mathbb{Z}})\,|\,h_{\ell }\hspace{0.6em}({\rm mod}\hspace{0.2em}\ell ^{n})\in B_{g}(\mathbb{Z}/\ell ^{n}\mathbb{Z})\}$
.
$\unicode[STIX]{x1D6E4}_{0}^{(g)}(\ell ^{n})=\{h\in \operatorname{GSp}_{2g}(\widehat{\mathbb{Z}})\,|\,h_{\ell }\hspace{0.6em}({\rm mod}\hspace{0.2em}\ell ^{n})\in B_{g}(\mathbb{Z}/\ell ^{n}\mathbb{Z})\}$
.
Let
![]() $N$
be an arbitrary positive integer. Write
$N$
be an arbitrary positive integer. Write
![]() $N=\prod _{i}\ell _{i}^{n_{i}}$
for some distinct primes
$N=\prod _{i}\ell _{i}^{n_{i}}$
for some distinct primes
![]() $\ell _{i}$
and some
$\ell _{i}$
and some
![]() $n_{i}\in \mathbb{N}$
. For a positive integer
$n_{i}\in \mathbb{N}$
. For a positive integer
![]() $N$
factoring as
$N$
factoring as
![]() $\prod _{i}\ell _{i}^{n_{i}}$
, we set
$\prod _{i}\ell _{i}^{n_{i}}$
, we set
![]() $\unicode[STIX]{x1D6E4}_{?}^{(g)}(N)=\bigcap _{i}\unicode[STIX]{x1D6E4}_{?}^{(g)}(\ell _{i}^{n_{i}})$
for
$\unicode[STIX]{x1D6E4}_{?}^{(g)}(N)=\bigcap _{i}\unicode[STIX]{x1D6E4}_{?}^{(g)}(\ell _{i}^{n_{i}})$
for
![]() $?=\varnothing ,0,1$
. For
$?=\varnothing ,0,1$
. For
![]() $g=1$
, we will omit the upper index (1).
$g=1$
, we will omit the upper index (1).
List of notation
In addition to the notation described above, we give the references to the pages where the following notation is introduced.

2 Preliminaries on eigenvarieties
In this section, we define the basic objects we are going to work with: weight spaces, Hecke algebras and eigenvarieties. We recall some of their properties.
2.1 The weight spaces
We choose once and for all
![]() $u=1+p$
as a generator of
$u=1+p$
as a generator of
![]() $\mathbb{Z}_{p}^{\times }$
. This choice determines an isomorphism
$\mathbb{Z}_{p}^{\times }$
. This choice determines an isomorphism
![]() $\mathbb{Z}_{p}^{\times }\cong (\mathbb{Z}/(p-1)\mathbb{Z})\times \mathbb{Z}_{p}$
. Let
$\mathbb{Z}_{p}^{\times }\cong (\mathbb{Z}/(p-1)\mathbb{Z})\times \mathbb{Z}_{p}$
. Let
![]() $g$
be a positive integer. Consider the Iwasawa algebra
$g$
be a positive integer. Consider the Iwasawa algebra
![]() $\mathbb{Z}_{p}[[(\mathbb{Z}_{p}^{\times })^{g}]]$
. A construction by Berthelot [Reference de JongdeJ95, §7] attaches to the formal scheme
$\mathbb{Z}_{p}[[(\mathbb{Z}_{p}^{\times })^{g}]]$
. A construction by Berthelot [Reference de JongdeJ95, §7] attaches to the formal scheme
![]() $\operatorname{Spf}\mathbb{Z}_{p}[[(\mathbb{Z}_{p}^{\times })^{g}]]$
a rigid analytic space that we denote by
$\operatorname{Spf}\mathbb{Z}_{p}[[(\mathbb{Z}_{p}^{\times })^{g}]]$
a rigid analytic space that we denote by
![]() ${\mathcal{W}}_{g}$
. If
${\mathcal{W}}_{g}$
. If
![]() $A$
is a
$A$
is a
![]() $\mathbb{Q}_{p}$
-algebra, the
$\mathbb{Q}_{p}$
-algebra, the
![]() $A$
-points of
$A$
-points of
![]() ${\mathcal{W}}_{g}$
are the continuous characters
${\mathcal{W}}_{g}$
are the continuous characters
![]() $(\mathbb{Z}_{p}^{\times })^{g}\rightarrow A^{\times }$
. Denote by
$(\mathbb{Z}_{p}^{\times })^{g}\rightarrow A^{\times }$
. Denote by
![]() $(\mathbb{Z}/(p-1)\mathbb{Z})^{\wedge ,g}$
the group of characters of
$(\mathbb{Z}/(p-1)\mathbb{Z})^{\wedge ,g}$
the group of characters of
![]() $(\mathbb{Z}/(p-1)\mathbb{Z})^{g}$
. The following map gives an isomorphism from
$(\mathbb{Z}/(p-1)\mathbb{Z})^{g}$
. The following map gives an isomorphism from
![]() ${\mathcal{W}}_{g}$
to a disjoint union of
${\mathcal{W}}_{g}$
to a disjoint union of
![]() $g$
-dimensional open discs
$g$
-dimensional open discs
![]() $B_{g}(0,1^{-})$
indexed by
$B_{g}(0,1^{-})$
indexed by
![]() $(\mathbb{Z}/(p-1)\mathbb{Z})^{\wedge ,g}$
:
$(\mathbb{Z}/(p-1)\mathbb{Z})^{\wedge ,g}$
:
We denote by
![]() ${\mathcal{W}}_{g}^{\circ }$
the connected component of
${\mathcal{W}}_{g}^{\circ }$
the connected component of
![]() ${\mathcal{W}}_{g}$
that maps to
${\mathcal{W}}_{g}$
that maps to
![]() $0\in (\mathbb{Z}/(p-1)\mathbb{Z})^{g}$
. We write
$0\in (\mathbb{Z}/(p-1)\mathbb{Z})^{g}$
. We write
![]() $\unicode[STIX]{x1D6EC}_{g}$
for the algebra
$\unicode[STIX]{x1D6EC}_{g}$
for the algebra
![]() $\mathbb{Z}_{p}[[T_{1},T_{2},\ldots ,T_{g}]]$
of formal series in
$\mathbb{Z}_{p}[[T_{1},T_{2},\ldots ,T_{g}]]$
of formal series in
![]() $g$
variables over
$g$
variables over
![]() $\mathbb{Z}_{p}$
. It is the ring of rigid analytic functions bounded by
$\mathbb{Z}_{p}$
. It is the ring of rigid analytic functions bounded by
![]() $1$
on a connected component of the weight space. The weight space
$1$
on a connected component of the weight space. The weight space
![]() ${\mathcal{W}}_{g}$
carries a universal character
${\mathcal{W}}_{g}$
carries a universal character
![]() $\unicode[STIX]{x1D705}_{{\mathcal{W}}_{g}}:\mathbb{Z}_{p}^{\times }\rightarrow \mathbb{Z}_{p}[[(\mathbb{Z}_{p}^{\times })^{g}]]^{\times }$
.
$\unicode[STIX]{x1D705}_{{\mathcal{W}}_{g}}:\mathbb{Z}_{p}^{\times }\rightarrow \mathbb{Z}_{p}[[(\mathbb{Z}_{p}^{\times })^{g}]]^{\times }$
.
We call arithmetic primes the primes of
![]() $\unicode[STIX]{x1D6EC}_{g}$
of the form
$\unicode[STIX]{x1D6EC}_{g}$
of the form
![]() $P_{\text{}\underline{k}}=(1+T_{1}-u^{k_{1}},1+T_{2}-u^{k_{2}},\ldots ,1+T_{g}-u^{k_{g}})$
for a
$P_{\text{}\underline{k}}=(1+T_{1}-u^{k_{1}},1+T_{2}-u^{k_{2}},\ldots ,1+T_{g}-u^{k_{g}})$
for a
![]() $g$
-tuple of integers
$g$
-tuple of integers
![]() $\text{}\underline{k}=(k_{1},k_{2},\ldots ,k_{g})$
(in the usual definition an auxiliary character can appear, but we will never need it). We say that a
$\text{}\underline{k}=(k_{1},k_{2},\ldots ,k_{g})$
(in the usual definition an auxiliary character can appear, but we will never need it). We say that a
![]() $\mathbb{Q}_{p}$
-point
$\mathbb{Q}_{p}$
-point
![]() $\unicode[STIX]{x1D705}:\mathbb{Z}_{p}^{\times }\rightarrow \mathbb{Q}_{p}^{\times }$
of
$\unicode[STIX]{x1D705}:\mathbb{Z}_{p}^{\times }\rightarrow \mathbb{Q}_{p}^{\times }$
of
![]() ${\mathcal{W}}_{g}^{\circ }$
is classical if it is the specialization of the universal character of
${\mathcal{W}}_{g}^{\circ }$
is classical if it is the specialization of the universal character of
![]() ${\mathcal{W}}_{g}$
at
${\mathcal{W}}_{g}$
at
![]() $P_{\text{}\underline{k}}$
, for some
$P_{\text{}\underline{k}}$
, for some
![]() $\text{}\underline{k}\in \mathbb{Z}^{g}$
.
$\text{}\underline{k}\in \mathbb{Z}^{g}$
.
2.2 The abstract Hecke algebras
Let
![]() $\ell$
be a prime. Let
$\ell$
be a prime. Let
![]() $G$
be a
$G$
be a
![]() $\mathbb{Z}$
-subgroup scheme of
$\mathbb{Z}$
-subgroup scheme of
![]() $\operatorname{GSp}_{2g}$
and let
$\operatorname{GSp}_{2g}$
and let
![]() $K\subset G(\mathbb{Q}_{\ell })$
be a compact open subgroup. For
$K\subset G(\mathbb{Q}_{\ell })$
be a compact open subgroup. For
![]() $\unicode[STIX]{x1D6FE}\in G(\mathbb{Q}_{\ell })$
we denote by
$\unicode[STIX]{x1D6FE}\in G(\mathbb{Q}_{\ell })$
we denote by
![]() $\unicode[STIX]{x1D7D9}([K\unicode[STIX]{x1D6FE}K])$
the characteristic function of the double coset
$\unicode[STIX]{x1D7D9}([K\unicode[STIX]{x1D6FE}K])$
the characteristic function of the double coset
![]() $[K\unicode[STIX]{x1D6FE}K]$
. Let
$[K\unicode[STIX]{x1D6FE}K]$
. Let
![]() ${\mathcal{H}}(G(\mathbb{Q}_{\ell }),K)$
be the
${\mathcal{H}}(G(\mathbb{Q}_{\ell }),K)$
be the
![]() $\mathbb{Q}$
-algebra generated by the functions
$\mathbb{Q}$
-algebra generated by the functions
![]() $\unicode[STIX]{x1D7D9}([K\unicode[STIX]{x1D6FE}K])$
for
$\unicode[STIX]{x1D7D9}([K\unicode[STIX]{x1D6FE}K])$
for
![]() $\unicode[STIX]{x1D6FE}\in G(\mathbb{Q}_{\ell })$
, equipped with the convolution product. We call spherical (or unramified) Hecke algebra of
$\unicode[STIX]{x1D6FE}\in G(\mathbb{Q}_{\ell })$
, equipped with the convolution product. We call spherical (or unramified) Hecke algebra of
![]() $\operatorname{GSp}_{2g}$
at
$\operatorname{GSp}_{2g}$
at
![]() $\ell$
the
$\ell$
the
![]() $\mathbb{Q}$
-algebra
$\mathbb{Q}$
-algebra
![]() ${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell }))$
. It is generated by the elements
${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell }))$
. It is generated by the elements
![]() $T_{\ell ,i}^{(g)}=\unicode[STIX]{x1D7D9}([\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell })\operatorname{diag}(\unicode[STIX]{x1D7D9}_{i},\ell \unicode[STIX]{x1D7D9}_{2g-2i},\ell ^{2}\unicode[STIX]{x1D7D9}_{i})\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell })])$
, for
$T_{\ell ,i}^{(g)}=\unicode[STIX]{x1D7D9}([\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell })\operatorname{diag}(\unicode[STIX]{x1D7D9}_{i},\ell \unicode[STIX]{x1D7D9}_{2g-2i},\ell ^{2}\unicode[STIX]{x1D7D9}_{i})\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell })])$
, for
![]() $i=0,1,\ldots g$
, and
$i=0,1,\ldots g$
, and
![]() $(T_{\ell ,0}^{(g)})^{-1}$
.
$(T_{\ell ,0}^{(g)})^{-1}$
.
The Hecke algebra
![]() ${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))$
carries a natural action of the Weyl group
${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))$
carries a natural action of the Weyl group
![]() $W_{g}=\mathscr{S}_{g}\ltimes (\mathbb{Z}/2\mathbb{Z})^{g}$
of
$W_{g}=\mathscr{S}_{g}\ltimes (\mathbb{Z}/2\mathbb{Z})^{g}$
of
![]() $\operatorname{GSp}_{2g}$
, where
$\operatorname{GSp}_{2g}$
, where
![]() $\mathscr{S}_{g}$
is the group of permutations of
$\mathscr{S}_{g}$
is the group of permutations of
![]() $\{1,2,\ldots ,g\}$
: on an element
$\{1,2,\ldots ,g\}$
: on an element
![]() $\operatorname{diag}(\unicode[STIX]{x1D708}t_{1},\ldots ,\unicode[STIX]{x1D708}t_{g},t_{g}^{-1},\ldots ,t_{1}^{-1})$
of the torus,
$\operatorname{diag}(\unicode[STIX]{x1D708}t_{1},\ldots ,\unicode[STIX]{x1D708}t_{g},t_{g}^{-1},\ldots ,t_{1}^{-1})$
of the torus,
![]() $\mathscr{S}_{g}$
acts by permuting the
$\mathscr{S}_{g}$
acts by permuting the
![]() $t_{i}$
and the non-trivial element in each
$t_{i}$
and the non-trivial element in each
![]() $\mathbb{Z}/2\mathbb{Z}$
sends
$\mathbb{Z}/2\mathbb{Z}$
sends
![]() $t_{i}$
to
$t_{i}$
to
![]() $t_{i}^{-1}$
. We denote the action of
$t_{i}^{-1}$
. We denote the action of
![]() $w\in W_{g}$
on
$w\in W_{g}$
on
![]() $t\in T(\mathbb{Q}_{\ell })$
by
$t\in T(\mathbb{Q}_{\ell })$
by
![]() $t\mapsto w.t$
. Via the twisted Satake transform, the algebra
$t\mapsto w.t$
. Via the twisted Satake transform, the algebra
![]() ${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))$
obtains a structure of Galois extension of
${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))$
obtains a structure of Galois extension of
![]() ${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell }))$
. Its Galois group is
${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell }))$
. Its Galois group is
![]() $W_{g}$
.
$W_{g}$
.
For
![]() $i=0,1,\ldots ,g$
, let
$i=0,1,\ldots ,g$
, let
![]() $t_{\ell ,i}^{(g)}=\unicode[STIX]{x1D7D9}([\operatorname{diag}(\unicode[STIX]{x1D7D9}_{i},\ell \unicode[STIX]{x1D7D9}_{2g-2i},\ell ^{2}\unicode[STIX]{x1D7D9}_{i})\mathbb{T}_{g}(\mathbb{Z}_{\ell })])$
. Note that
$t_{\ell ,i}^{(g)}=\unicode[STIX]{x1D7D9}([\operatorname{diag}(\unicode[STIX]{x1D7D9}_{i},\ell \unicode[STIX]{x1D7D9}_{2g-2i},\ell ^{2}\unicode[STIX]{x1D7D9}_{i})\mathbb{T}_{g}(\mathbb{Z}_{\ell })])$
. Note that
![]() $t_{\ell ,0}^{(g)}=S_{\operatorname{GSp}_{2g}}^{T_{g}}(T_{\ell ,0}^{g})$
. The set
$t_{\ell ,0}^{(g)}=S_{\operatorname{GSp}_{2g}}^{T_{g}}(T_{\ell ,0}^{g})$
. The set
![]() $(t_{\ell ,i}^{(g)})_{i=1,\ldots ,g}$
generates the extension
$(t_{\ell ,i}^{(g)})_{i=1,\ldots ,g}$
generates the extension
![]() ${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))$
over
${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))$
over
![]() ${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell }))$
.
${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell }))$
.
We call an element
![]() $\unicode[STIX]{x1D6FE}\in T_{g}(\mathbb{Z}_{\ell })$
dilating if
$\unicode[STIX]{x1D6FE}\in T_{g}(\mathbb{Z}_{\ell })$
dilating if
![]() $v_{p}(\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE}))\leqslant 0$
for every positive root
$v_{p}(\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D6FE}))\leqslant 0$
for every positive root
![]() $\unicode[STIX]{x1D6FC}$
. Let
$\unicode[STIX]{x1D6FC}$
. Let
![]() $T_{g}(\mathbb{Z}_{\ell })^{-}$
be the subset of
$T_{g}(\mathbb{Z}_{\ell })^{-}$
be the subset of
![]() $T_{g}(\mathbb{Z}_{\ell })$
consisting of dilating elements and let
$T_{g}(\mathbb{Z}_{\ell })$
consisting of dilating elements and let
![]() ${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))^{-}$
be the
${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))^{-}$
be the
![]() $\mathbb{Q}$
-subalgebra of
$\mathbb{Q}$
-subalgebra of
![]() ${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))$
generated by the functions
${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))$
generated by the functions
![]() $\unicode[STIX]{x1D7D9}([\unicode[STIX]{x1D6FE}T_{g}(\mathbb{Z}_{\ell })])$
with
$\unicode[STIX]{x1D7D9}([\unicode[STIX]{x1D6FE}T_{g}(\mathbb{Z}_{\ell })])$
with
![]() $\unicode[STIX]{x1D6FE}\in T_{g}(\mathbb{Q}_{\ell })^{-}$
. The functions
$\unicode[STIX]{x1D6FE}\in T_{g}(\mathbb{Q}_{\ell })^{-}$
. The functions
![]() $\unicode[STIX]{x1D7D9}([\unicode[STIX]{x1D6FE}T_{g}(\mathbb{Z}_{\ell })])$
with
$\unicode[STIX]{x1D7D9}([\unicode[STIX]{x1D6FE}T_{g}(\mathbb{Z}_{\ell })])$
with
![]() $\unicode[STIX]{x1D6FE}\in T_{g}(\mathbb{Q}_{\ell })^{-}$
also form a basis of
$\unicode[STIX]{x1D6FE}\in T_{g}(\mathbb{Q}_{\ell })^{-}$
also form a basis of
![]() ${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))^{-}$
as a
${\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))^{-}$
as a
![]() $\mathbb{Q}$
-vector space.
$\mathbb{Q}$
-vector space.
Let
![]() ${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),I_{g,\ell })^{-}$
be the subalgebra of
${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),I_{g,\ell })^{-}$
be the subalgebra of
![]() ${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),I_{g,\ell })$
generated by the functions
${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),I_{g,\ell })$
generated by the functions
![]() $\unicode[STIX]{x1D7D9}([I_{g,\ell }\unicode[STIX]{x1D6FE}I_{g,\ell }])$
with
$\unicode[STIX]{x1D7D9}([I_{g,\ell }\unicode[STIX]{x1D6FE}I_{g,\ell }])$
with
![]() $\unicode[STIX]{x1D6FE}\in T(\mathbb{Z}_{\ell })^{-}$
. We call
$\unicode[STIX]{x1D6FE}\in T(\mathbb{Z}_{\ell })^{-}$
. We call
![]() ${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),I_{g,\ell })^{-}$
the dilating Iwahori–Hecke algebra at
${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),I_{g,\ell })^{-}$
the dilating Iwahori–Hecke algebra at
![]() $\ell$
. It is generated by the elements
$\ell$
. It is generated by the elements
![]() $U_{\ell ,i}^{(g)}=\unicode[STIX]{x1D7D9}([I_{g,\ell }\operatorname{diag}(\unicode[STIX]{x1D7D9}_{i},\ell \unicode[STIX]{x1D7D9}_{2g-2i},\ell ^{2}\unicode[STIX]{x1D7D9}_{i})I_{g,\ell }])$
, for
$U_{\ell ,i}^{(g)}=\unicode[STIX]{x1D7D9}([I_{g,\ell }\operatorname{diag}(\unicode[STIX]{x1D7D9}_{i},\ell \unicode[STIX]{x1D7D9}_{2g-2i},\ell ^{2}\unicode[STIX]{x1D7D9}_{i})I_{g,\ell }])$
, for
![]() $i=0,1,\ldots ,g$
, and
$i=0,1,\ldots ,g$
, and
![]() $(U_{\ell ,0}^{(g)})^{-1}$
.
$(U_{\ell ,0}^{(g)})^{-1}$
.
We define a morphism of
![]() $\mathbb{Q}$
-algebras
$\mathbb{Q}$
-algebras
![]() $\unicode[STIX]{x1D704}_{I_{g,\ell }}^{T_{g}}:{\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),I_{g,\ell })^{-}\rightarrow {\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))^{-}$
by sending
$\unicode[STIX]{x1D704}_{I_{g,\ell }}^{T_{g}}:{\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),I_{g,\ell })^{-}\rightarrow {\mathcal{H}}(T_{g}(\mathbb{Q}_{\ell }),T_{g}(\mathbb{Z}_{\ell }))^{-}$
by sending
![]() $\unicode[STIX]{x1D7D9}(I_{g,\ell }\unicode[STIX]{x1D6FE}I_{g,\ell })$
to
$\unicode[STIX]{x1D7D9}(I_{g,\ell }\unicode[STIX]{x1D6FE}I_{g,\ell })$
to
![]() $\unicode[STIX]{x1D7D9}(T_{g}(\mathbb{Z}_{\ell })\unicode[STIX]{x1D6FE}T_{g}(\mathbb{Z}_{\ell }))$
for every
$\unicode[STIX]{x1D7D9}(T_{g}(\mathbb{Z}_{\ell })\unicode[STIX]{x1D6FE}T_{g}(\mathbb{Z}_{\ell }))$
for every
![]() $\unicode[STIX]{x1D6FE}\in T(\mathbb{Z}_{\ell })^{-}$
. The map
$\unicode[STIX]{x1D6FE}\in T(\mathbb{Z}_{\ell })^{-}$
. The map
![]() $\unicode[STIX]{x1D704}_{I_{g,\ell }}^{T_{g}}$
is an isomorphism; this can be proved as [Reference Bellaïche and ChenevierBC09, Proposition 6.4.1].
$\unicode[STIX]{x1D704}_{I_{g,\ell }}^{T_{g}}$
is an isomorphism; this can be proved as [Reference Bellaïche and ChenevierBC09, Proposition 6.4.1].
Let
![]() $p$
be a prime and
$p$
be a prime and
![]() $N$
be a positive integer such that
$N$
be a positive integer such that
![]() $(N,p)=1$
. Set
$(N,p)=1$
. Set
We call
![]() ${\mathcal{H}}_{g}^{N}$
the abstract Hecke algebra spherical outside
${\mathcal{H}}_{g}^{N}$
the abstract Hecke algebra spherical outside
![]() $N$
and Iwahoric dilating at
$N$
and Iwahoric dilating at
![]() $p$
. With an abuse of notation, we will consider the elements of one of the local algebras as elements of
$p$
. With an abuse of notation, we will consider the elements of one of the local algebras as elements of
![]() ${\mathcal{H}}_{g}^{N}$
by tensoring with
${\mathcal{H}}_{g}^{N}$
by tensoring with
![]() $1$
at all the other primes.
$1$
at all the other primes.
2.2.1 The Hecke polynomials
We record here some explicit formulas for the minimal polynomials
![]() $P_{\operatorname{min}}(t_{\ell ,i}^{(g)};X)$
of the elements
$P_{\operatorname{min}}(t_{\ell ,i}^{(g)};X)$
of the elements
![]() $t_{\ell ,i}^{(g)}$
over
$t_{\ell ,i}^{(g)}$
over
![]() ${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell }))$
when
${\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{2g}(\mathbb{Z}_{\ell }))$
when
![]() $g$
is
$g$
is
![]() $1$
or
$1$
or
![]() $2$
.
$2$
.
For
![]() $g=1$
, the element
$g=1$
, the element
![]() $t_{\ell ,1}^{(1)}=\unicode[STIX]{x1D7D9}([\operatorname{diag}(1,\ell )T_{1}(\mathbb{Z}_{\ell })])$
generates the degree two extension
$t_{\ell ,1}^{(1)}=\unicode[STIX]{x1D7D9}([\operatorname{diag}(1,\ell )T_{1}(\mathbb{Z}_{\ell })])$
generates the degree two extension
![]() ${\mathcal{H}}(T_{1}(\mathbb{Q}_{\ell }),T_{1}(\mathbb{Z}_{\ell }))$
of
${\mathcal{H}}(T_{1}(\mathbb{Q}_{\ell }),T_{1}(\mathbb{Z}_{\ell }))$
of
![]() ${\mathcal{H}}(\operatorname{GL}_{2}(\mathbb{Q}_{\ell }),\operatorname{GL}_{2}(\mathbb{Z}_{\ell }))$
. Let
${\mathcal{H}}(\operatorname{GL}_{2}(\mathbb{Q}_{\ell }),\operatorname{GL}_{2}(\mathbb{Z}_{\ell }))$
. Let
![]() $w$
be the only non-trivial element of the Weyl group of
$w$
be the only non-trivial element of the Weyl group of
![]() $\operatorname{GL}_{2}$
. The minimal polynomial of
$\operatorname{GL}_{2}$
. The minimal polynomial of
![]() $t_{\ell ,1}^{(1)}$
is
$t_{\ell ,1}^{(1)}$
is
![]() $P_{\operatorname{min}}(t_{\ell ,1}^{(1)})(X)=(X-t_{\ell ,1}^{(1)})(X-(t_{\ell ,1}^{(1)})^{w})$
. An explicit calculation gives
$P_{\operatorname{min}}(t_{\ell ,1}^{(1)})(X)=(X-t_{\ell ,1}^{(1)})(X-(t_{\ell ,1}^{(1)})^{w})$
. An explicit calculation gives
For
![]() $g=2$
, the degree eight extension
$g=2$
, the degree eight extension
![]() ${\mathcal{H}}(T_{2}(\mathbb{Q}_{\ell }),T_{2}(\mathbb{Z}_{\ell }))$
over
${\mathcal{H}}(T_{2}(\mathbb{Q}_{\ell }),T_{2}(\mathbb{Z}_{\ell }))$
over
![]() ${\mathcal{H}}(\operatorname{GSp}_{4}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{4}(\mathbb{Z}_{\ell }))$
is generated by
${\mathcal{H}}(\operatorname{GSp}_{4}(\mathbb{Q}_{\ell }),\operatorname{GSp}_{4}(\mathbb{Z}_{\ell }))$
is generated by
![]() $t_{\ell ,1}^{(2)}=\unicode[STIX]{x1D7D9}([\operatorname{diag}(1,\ell ,\ell ,\ell ^{2})T_{2}(\mathbb{Z}_{\ell })])$
and
$t_{\ell ,1}^{(2)}=\unicode[STIX]{x1D7D9}([\operatorname{diag}(1,\ell ,\ell ,\ell ^{2})T_{2}(\mathbb{Z}_{\ell })])$
and
![]() $t_{\ell ,2}^{(2)}=\unicode[STIX]{x1D7D9}([\operatorname{diag}(1,1,\ell ,\ell )T_{2}(\mathbb{Z}_{\ell })])$
. Each of them has an orbit of order four under the action of the Weyl group. If
$t_{\ell ,2}^{(2)}=\unicode[STIX]{x1D7D9}([\operatorname{diag}(1,1,\ell ,\ell )T_{2}(\mathbb{Z}_{\ell })])$
. Each of them has an orbit of order four under the action of the Weyl group. If
![]() $t=\operatorname{diag}(\unicode[STIX]{x1D708}t_{1},\unicode[STIX]{x1D708}t_{2},t_{1}^{-1},t_{2}^{-1})$
is an element of the torus we denote by
$t=\operatorname{diag}(\unicode[STIX]{x1D708}t_{1},\unicode[STIX]{x1D708}t_{2},t_{1}^{-1},t_{2}^{-1})$
is an element of the torus we denote by
![]() $w_{0}$
,
$w_{0}$
,
![]() $w_{1}$
,
$w_{1}$
,
![]() $w_{2}$
the generators of the Weyl group satisfying
$w_{2}$
the generators of the Weyl group satisfying
![]() $t^{w_{0}}=\operatorname{diag}(\unicode[STIX]{x1D708}t_{2},\unicode[STIX]{x1D708}t_{1},t_{2}^{-1},t_{1}^{-1})$
,
$t^{w_{0}}=\operatorname{diag}(\unicode[STIX]{x1D708}t_{2},\unicode[STIX]{x1D708}t_{1},t_{2}^{-1},t_{1}^{-1})$
,
![]() $t^{w_{1}}=\operatorname{diag}(\unicode[STIX]{x1D708}t_{1}^{-1},\unicode[STIX]{x1D708}t_{2},t_{1},t_{2}^{-1})$
,
$t^{w_{1}}=\operatorname{diag}(\unicode[STIX]{x1D708}t_{1}^{-1},\unicode[STIX]{x1D708}t_{2},t_{1},t_{2}^{-1})$
,
![]() $t^{w_{2}}=\operatorname{diag}(\unicode[STIX]{x1D708}t_{1},\unicode[STIX]{x1D708}t_{2}^{-1},t_{1}^{-1},t_{2})$
. Note that
$t^{w_{2}}=\operatorname{diag}(\unicode[STIX]{x1D708}t_{1},\unicode[STIX]{x1D708}t_{2}^{-1},t_{1}^{-1},t_{2})$
. Note that
![]() $t_{\ell ,2}^{(2)}$
is invariant under
$t_{\ell ,2}^{(2)}$
is invariant under
![]() $w_{0}$
. The calculation in the proof of [Reference AndrianovAnd87, Lemma 3.3.35] gives
$w_{0}$
. The calculation in the proof of [Reference AndrianovAnd87, Lemma 3.3.35] gives
 $$\begin{eqnarray}\displaystyle P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X) & = & \displaystyle (X-t_{\ell ,2}^{(2)})(X-(t_{\ell ,2}^{(2)})^{w_{1}})(X-(t_{\ell ,2}^{(2)})^{w_{2}})(X-(t_{\ell ,2}^{(2)})^{w_{1}w_{2}})\nonumber\\ \displaystyle & = & \displaystyle X^{4}-T_{\ell ,2}^{(2)}X^{3}+((T_{\ell ,2}^{(2)})^{2}-T_{\ell ,1}^{(2)}-\ell ^{2}T_{\ell ,0}^{(2)})X^{2}-\ell ^{3}T_{\ell ,2}^{(2)}T_{\ell ,0}^{(2)}X+\ell ^{6}(T_{\ell ,0}^{(2)})^{2}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X) & = & \displaystyle (X-t_{\ell ,2}^{(2)})(X-(t_{\ell ,2}^{(2)})^{w_{1}})(X-(t_{\ell ,2}^{(2)})^{w_{2}})(X-(t_{\ell ,2}^{(2)})^{w_{1}w_{2}})\nonumber\\ \displaystyle & = & \displaystyle X^{4}-T_{\ell ,2}^{(2)}X^{3}+((T_{\ell ,2}^{(2)})^{2}-T_{\ell ,1}^{(2)}-\ell ^{2}T_{\ell ,0}^{(2)})X^{2}-\ell ^{3}T_{\ell ,2}^{(2)}T_{\ell ,0}^{(2)}X+\ell ^{6}(T_{\ell ,0}^{(2)})^{2}.\end{eqnarray}$$
2.2.2 Normalized systems of Hecke eigenvalues
Let
![]() $f$
be a classical
$f$
be a classical
![]() $\operatorname{GSp}_{2g}$
-eigenform of level
$\operatorname{GSp}_{2g}$
-eigenform of level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)\,\cap \,\unicode[STIX]{x1D6E4}_{0}(p)$
and weight
$\unicode[STIX]{x1D6E4}_{1}(N)\,\cap \,\unicode[STIX]{x1D6E4}_{0}(p)$
and weight
![]() $\text{}\underline{k}=(k_{1},k_{2},\ldots ,k_{g})$
. Let
$\text{}\underline{k}=(k_{1},k_{2},\ldots ,k_{g})$
. Let
![]() $\unicode[STIX]{x1D712}:{\mathcal{H}}_{g}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the system of Hecke eigenvalues associated with
$\unicode[STIX]{x1D712}:{\mathcal{H}}_{g}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the system of Hecke eigenvalues associated with
![]() $f$
.
$f$
.
Definition 2.1. For
![]() $g\in \{1,2\}$
, let
$g\in \{1,2\}$
, let
![]() $\unicode[STIX]{x1D712}^{\operatorname{norm}}:{\mathcal{H}}_{g}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the character defined by:
$\unicode[STIX]{x1D712}^{\operatorname{norm}}:{\mathcal{H}}_{g}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the character defined by:
–
 $\unicode[STIX]{x1D712}^{\operatorname{norm}}|_{{\mathcal{H}}_{g}^{Np}}=\unicode[STIX]{x1D712}|_{{\mathcal{H}}_{g}^{Np}}$
;
$\unicode[STIX]{x1D712}^{\operatorname{norm}}|_{{\mathcal{H}}_{g}^{Np}}=\unicode[STIX]{x1D712}|_{{\mathcal{H}}_{g}^{Np}}$
;–
 $\unicode[STIX]{x1D712}^{\operatorname{norm}}(U_{p,i}^{(g)})=p^{-\!\sum _{j=1}^{g-i}(k_{j}-j)}$
for
$\unicode[STIX]{x1D712}^{\operatorname{norm}}(U_{p,i}^{(g)})=p^{-\!\sum _{j=1}^{g-i}(k_{j}-j)}$
for
 $i=1,2,\ldots ,g$
(where the exponent of
$i=1,2,\ldots ,g$
(where the exponent of
 $p$
is
$p$
is
 $0$
for
$0$
for
 $i=g$
).
$i=g$
).
We call
![]() $\unicode[STIX]{x1D712}^{\operatorname{norm}}$
the normalized system of Hecke eigenvalues associated with
$\unicode[STIX]{x1D712}^{\operatorname{norm}}$
the normalized system of Hecke eigenvalues associated with
![]() $f$
.
$f$
.
2.3 The cuspidal
 $\operatorname{GSp}_{2g}$
-eigenvariety
$\operatorname{GSp}_{2g}$
-eigenvariety
Let
![]() $g$
be a positive integer. Let
$g$
be a positive integer. Let
![]() $p$
be an odd prime and
$p$
be an odd prime and
![]() $N$
a positive integer such that
$N$
a positive integer such that
![]() $(N,p)=1$
. Let
$(N,p)=1$
. Let
![]() ${\mathcal{H}}_{g}^{N}$
be the abstract Hecke algebra for
${\mathcal{H}}_{g}^{N}$
be the abstract Hecke algebra for
![]() $\operatorname{GSp}_{2g}$
, spherical outside
$\operatorname{GSp}_{2g}$
, spherical outside
![]() $N$
and Iwahoric dilating at
$N$
and Iwahoric dilating at
![]() $p$
. Let
$p$
. Let
![]() ${\mathcal{W}}_{g}$
be the
${\mathcal{W}}_{g}$
be the
![]() $g$
-dimensional weight space. For every affinoid
$g$
-dimensional weight space. For every affinoid
![]() $A=\operatorname{Spm}R\subset {\mathcal{W}}_{g}$
and every sufficiently large rational number
$A=\operatorname{Spm}R\subset {\mathcal{W}}_{g}$
and every sufficiently large rational number
![]() $w$
, Andreatta, Iovita and Pilloni [Reference Andreatta, Iovita and PilloniAIP15, §8.2] defined a Banach
$w$
, Andreatta, Iovita and Pilloni [Reference Andreatta, Iovita and PilloniAIP15, §8.2] defined a Banach
![]() $R$
-module
$R$
-module
![]() $M_{g}(A,w)$
of
$M_{g}(A,w)$
of
![]() $w$
-overconvergent cuspidal
$w$
-overconvergent cuspidal
![]() $\operatorname{GSp}_{2g}$
-modular forms of weight
$\operatorname{GSp}_{2g}$
-modular forms of weight
![]() $\unicode[STIX]{x1D705}_{A}$
and tame level
$\unicode[STIX]{x1D705}_{A}$
and tame level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
. For each pair
$\unicode[STIX]{x1D6E4}_{1}(N)$
. For each pair
![]() $(A,w)$
there is an action
$(A,w)$
there is an action
![]() $\unicode[STIX]{x1D719}_{A,w}^{g}:{\mathcal{H}}_{g}^{N}\rightarrow \operatorname{End}_{R,\operatorname{cont}}M_{g}(A,w)$
. Set
$\unicode[STIX]{x1D719}_{A,w}^{g}:{\mathcal{H}}_{g}^{N}\rightarrow \operatorname{End}_{R,\operatorname{cont}}M_{g}(A,w)$
. Set
![]() $U_{p}^{(g)}=\prod _{i=1}^{g}U_{p,g}^{(g)}$
. It is shown in [Reference Andreatta, Iovita and PilloniAIP15, §8.1] that
$U_{p}^{(g)}=\prod _{i=1}^{g}U_{p,g}^{(g)}$
. It is shown in [Reference Andreatta, Iovita and PilloniAIP15, §8.1] that
![]() $({\mathcal{W}}_{g},{\mathcal{H}}_{g}^{N},(M_{g}(A,w))_{A,w},(\unicode[STIX]{x1D719}^{g})_{A,w},U_{p}^{(g)})$
is an eigenvariety datum in the sense of [Reference BuzzardBuz07, §5]. Buzzard’s ‘eigenvariety machine’ [Reference BuzzardBuz07, Construction 5.7] produces from this datum a rigid analytic variety over
$({\mathcal{W}}_{g},{\mathcal{H}}_{g}^{N},(M_{g}(A,w))_{A,w},(\unicode[STIX]{x1D719}^{g})_{A,w},U_{p}^{(g)})$
is an eigenvariety datum in the sense of [Reference BuzzardBuz07, §5]. Buzzard’s ‘eigenvariety machine’ [Reference BuzzardBuz07, Construction 5.7] produces from this datum a rigid analytic variety over
![]() $\mathbb{Q}_{p}$
, equidimensional of dimension
$\mathbb{Q}_{p}$
, equidimensional of dimension
![]() $g$
. We call it the
$g$
. We call it the
![]() $\operatorname{GSp}_{2g}$
-eigenvariety of tame level
$\operatorname{GSp}_{2g}$
-eigenvariety of tame level
![]() $N$
and we denote it by
$N$
and we denote it by
![]() ${\mathcal{D}}_{g}^{N}$
. It is equipped with a weight morphism
${\mathcal{D}}_{g}^{N}$
. It is equipped with a weight morphism
![]() $w_{g}:{\mathcal{D}}_{g}^{N}\rightarrow {\mathcal{W}}_{g}$
and a homomorphism
$w_{g}:{\mathcal{D}}_{g}^{N}\rightarrow {\mathcal{W}}_{g}$
and a homomorphism
![]() $\unicode[STIX]{x1D713}_{g}:{\mathcal{H}}_{g}^{N}\rightarrow {\mathcal{O}}({\mathcal{D}}_{g}^{N})$
, that interpolates the normalized systems of Hecke eigenvalues of classical cuspidal
$\unicode[STIX]{x1D713}_{g}:{\mathcal{H}}_{g}^{N}\rightarrow {\mathcal{O}}({\mathcal{D}}_{g}^{N})$
, that interpolates the normalized systems of Hecke eigenvalues of classical cuspidal
![]() $\operatorname{GSp}_{2g}$
-eigenforms of tame level
$\operatorname{GSp}_{2g}$
-eigenforms of tame level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
. The images of the elements
$\unicode[STIX]{x1D6E4}_{1}(N)$
. The images of the elements
![]() $T_{i,\ell }^{(g)}$
and
$T_{i,\ell }^{(g)}$
and
![]() $U_{i,p}^{(g)}$
,
$U_{i,p}^{(g)}$
,
![]() $1\leqslant i\leqslant g$
, belong to
$1\leqslant i\leqslant g$
, belong to
![]() ${\mathcal{O}}({\mathcal{D}}_{g}^{N})^{\circ }$
.
${\mathcal{O}}({\mathcal{D}}_{g}^{N})^{\circ }$
.
When
![]() $g=1$
we call
$g=1$
we call
![]() ${\mathcal{D}}_{1}^{N}$
the eigencurve. It was constructed by Coleman and Mazur in [Reference Coleman and MazurCM98] for
${\mathcal{D}}_{1}^{N}$
the eigencurve. It was constructed by Coleman and Mazur in [Reference Coleman and MazurCM98] for
![]() $N=1$
and
$N=1$
and
![]() $p>2$
, building on earlier ideas of Coleman. Their construction was extended to all
$p>2$
, building on earlier ideas of Coleman. Their construction was extended to all
![]() $N$
and
$N$
and
![]() $p$
by Buzzard in [Reference BuzzardBuz07].
$p$
by Buzzard in [Reference BuzzardBuz07].
We call a point
![]() $x\in {\mathcal{D}}_{g}^{N}(\mathbb{C}_{p})$
classical if the evaluation of
$x\in {\mathcal{D}}_{g}^{N}(\mathbb{C}_{p})$
classical if the evaluation of
![]() $\unicode[STIX]{x1D713}_{g}$
at
$\unicode[STIX]{x1D713}_{g}$
at
![]() $x$
is the Hecke eigensystem a classical
$x$
is the Hecke eigensystem a classical
![]() $\operatorname{GSp}_{2g}$
-eigenform
$\operatorname{GSp}_{2g}$
-eigenform
![]() $f$
of level
$f$
of level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
and weight
$\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
and weight
![]() $w_{g}(x)$
. In this case,
$w_{g}(x)$
. In this case,
![]() $w_{g}(x)$
is clearly a classical weight.
$w_{g}(x)$
is clearly a classical weight.
There is a slope function
![]() $\operatorname{sl}:{\mathcal{D}}_{g}^{N}(\mathbb{C}_{p})\rightarrow \mathbb{R}^{+}$
defined as the
$\operatorname{sl}:{\mathcal{D}}_{g}^{N}(\mathbb{C}_{p})\rightarrow \mathbb{R}^{+}$
defined as the
![]() $p$
-adic valuation of
$p$
-adic valuation of
![]() $\unicode[STIX]{x1D713}_{g}(U_{p,g}^{(g)})$
. Let
$\unicode[STIX]{x1D713}_{g}(U_{p,g}^{(g)})$
. Let
![]() $x$
be a
$x$
be a
![]() $\overline{\mathbb{Q}}_{p}$
-point of
$\overline{\mathbb{Q}}_{p}$
-point of
![]() ${\mathcal{D}}_{g}^{N}$
of weight
${\mathcal{D}}_{g}^{N}$
of weight
![]() $\text{}\underline{k}=(k_{1},k_{2},\ldots ,k_{g})\in \mathbb{Z}^{g}$
, so that
$\text{}\underline{k}=(k_{1},k_{2},\ldots ,k_{g})\in \mathbb{Z}^{g}$
, so that
![]() $k_{1}\geqslant k_{2}\geqslant \cdots \geqslant k_{g}$
. We recall the following result.
$k_{1}\geqslant k_{2}\geqslant \cdots \geqslant k_{g}$
. We recall the following result.
Proposition 2.2 (Coleman [Reference ColemanCol96, Theorem 6.1] when
 $g=1$
; Bijakowski, Pilloni and Stroh [Reference Bijakowski, Pilloni and StrohBPS16, Theorem 5.3.1, see also Remark 1 in the Introduction] when
$g=1$
; Bijakowski, Pilloni and Stroh [Reference Bijakowski, Pilloni and StrohBPS16, Theorem 5.3.1, see also Remark 1 in the Introduction] when
 $g>1$
).
$g>1$
).
If
![]() $\operatorname{sl}(x)<k_{g}-g(g+1)/2$
, then the point
$\operatorname{sl}(x)<k_{g}-g(g+1)/2$
, then the point
![]() $x$
is classical.
$x$
is classical.
2.3.1 The non-CM eigencurve
We say that a classical point of
![]() ${\mathcal{D}}_{1}^{N}$
is a CM point if it corresponds to a classical CM modular form. We say that an irreducible component of
${\mathcal{D}}_{1}^{N}$
is a CM point if it corresponds to a classical CM modular form. We say that an irreducible component of
![]() ${\mathcal{D}}_{1}^{N}$
is a CM component if all its classical specializations are CM points.
${\mathcal{D}}_{1}^{N}$
is a CM component if all its classical specializations are CM points.
Remark 2.3. By [Reference HidaHid15, Proposition 5.1], if an ordinary irreducible component of the eigencurve contains a classical CM eigenform of weight
![]() $k\geqslant 2$
, then the component is CM. In contrast, the CM classical points of the positive slope eigencurve form a discrete set. This is a consequence of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Corollary 3.6], where it is shown that the eigencurve
$k\geqslant 2$
, then the component is CM. In contrast, the CM classical points of the positive slope eigencurve form a discrete set. This is a consequence of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Corollary 3.6], where it is shown that the eigencurve
![]() ${\mathcal{D}}^{+,\leqslant h}$
contains a finite number of CM classical points.
${\mathcal{D}}^{+,\leqslant h}$
contains a finite number of CM classical points.
Let
![]() ${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
be the Zariski-closure in
${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
be the Zariski-closure in
![]() ${\mathcal{D}}_{1}^{N}$
of the set of non-CM classical points. We call
${\mathcal{D}}_{1}^{N}$
of the set of non-CM classical points. We call
![]() ${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
the non-CM eigencurve. The upper index
${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
the non-CM eigencurve. The upper index
![]() ${\mathcal{G}}$
stands for ‘general’, because CM components are exceptional among the irreducible components of
${\mathcal{G}}$
stands for ‘general’, because CM components are exceptional among the irreducible components of
![]() ${\mathcal{D}}_{1}^{N}$
.
${\mathcal{D}}_{1}^{N}$
.
Remark 2.4. It follows from Remark 2.3 that
![]() ${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
is the union of all the non-CM irreducible components of
${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
is the union of all the non-CM irreducible components of
![]() ${\mathcal{D}}_{1}^{N}$
. In particular,
${\mathcal{D}}_{1}^{N}$
. In particular,
![]() ${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
is equidimensional of dimension
${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
is equidimensional of dimension
![]() $1$
and it contains the positive slope eigencurve. Moreover the set of non-CM classical points is a Zariski-dense and accumulation subset of
$1$
and it contains the positive slope eigencurve. Moreover the set of non-CM classical points is a Zariski-dense and accumulation subset of
![]() ${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
.
${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
.
2.4 The Galois pseudocharacters on the eigenvarieties
In this section,
![]() $p$
is a fixed prime,
$p$
is a fixed prime,
![]() $M$
is a positive integer prime to
$M$
is a positive integer prime to
![]() $p$
and
$p$
and
![]() $g$
is
$g$
is
![]() $1$
or
$1$
or
![]() $2$
. For a point
$2$
. For a point
![]() $x\in {\mathcal{D}}_{g}^{M}(\mathbb{C}_{p})$
, we denote by
$x\in {\mathcal{D}}_{g}^{M}(\mathbb{C}_{p})$
, we denote by
![]() $\operatorname{ev}_{x}:{\mathcal{O}}({\mathcal{D}}_{g}^{M})\rightarrow \mathbb{C}_{p}$
both the evaluation at
$\operatorname{ev}_{x}:{\mathcal{O}}({\mathcal{D}}_{g}^{M})\rightarrow \mathbb{C}_{p}$
both the evaluation at
![]() $x$
and the map
$x$
and the map
![]() $\operatorname{GSp}_{2g}({\mathcal{O}}({\mathcal{D}}_{g}^{M}))\rightarrow \operatorname{GSp}_{2g}(\mathbb{C}_{p})$
induced by
$\operatorname{GSp}_{2g}({\mathcal{O}}({\mathcal{D}}_{g}^{M}))\rightarrow \operatorname{GSp}_{2g}(\mathbb{C}_{p})$
induced by
![]() $\operatorname{ev}_{x}$
. Recall that the
$\operatorname{ev}_{x}$
. Recall that the
![]() $\operatorname{GSp}_{2g}$
-eigenvariety
$\operatorname{GSp}_{2g}$
-eigenvariety
![]() ${\mathcal{D}}_{g}^{M}$
is endowed with a morphism
${\mathcal{D}}_{g}^{M}$
is endowed with a morphism
![]() $\unicode[STIX]{x1D713}_{g}:{\mathcal{H}}_{g}^{M}\rightarrow {\mathcal{O}}({\mathcal{D}}_{g}^{M})$
that interpolates the normalized systems of Hecke eigenvalues associated with the cuspidal
$\unicode[STIX]{x1D713}_{g}:{\mathcal{H}}_{g}^{M}\rightarrow {\mathcal{O}}({\mathcal{D}}_{g}^{M})$
that interpolates the normalized systems of Hecke eigenvalues associated with the cuspidal
![]() $\operatorname{GSp}_{2g}$
-eigenforms of level
$\operatorname{GSp}_{2g}$
-eigenforms of level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
. Also recall that the images of
$\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
. Also recall that the images of
![]() $T_{i,\ell }^{(g)}$
and
$T_{i,\ell }^{(g)}$
and
![]() $U_{i,p}^{(g)}$
,
$U_{i,p}^{(g)}$
,
![]() $1\leqslant i\leqslant g$
, are elements of
$1\leqslant i\leqslant g$
, are elements of
![]() ${\mathcal{O}}({\mathcal{D}}_{g}^{M})^{\circ }$
. Let
${\mathcal{O}}({\mathcal{D}}_{g}^{M})^{\circ }$
. Let
![]() $S^{\operatorname{cl}}$
denote the set of classical
$S^{\operatorname{cl}}$
denote the set of classical
![]() $\overline{\mathbb{Q}}_{p}$
-points of
$\overline{\mathbb{Q}}_{p}$
-points of
![]() ${\mathcal{D}}_{g}^{M}$
. For
${\mathcal{D}}_{g}^{M}$
. For
![]() $x\in S^{\operatorname{cl}}$
let
$x\in S^{\operatorname{cl}}$
let
![]() $\unicode[STIX]{x1D713}_{x}=\operatorname{ev}_{x}\circ \,\unicode[STIX]{x1D713}_{g}$
. Let
$\unicode[STIX]{x1D713}_{x}=\operatorname{ev}_{x}\circ \,\unicode[STIX]{x1D713}_{g}$
. Let
![]() $f_{x}$
be the classical
$f_{x}$
be the classical
![]() $\operatorname{GSp}_{2g}$
-eigenform having system of Hecke eigenvalues
$\operatorname{GSp}_{2g}$
-eigenform having system of Hecke eigenvalues
![]() $\unicode[STIX]{x1D713}_{x}$
. Let
$\unicode[STIX]{x1D713}_{x}$
. Let
![]() $\unicode[STIX]{x1D70C}_{x}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{2g}(\overline{\mathbb{Q}}_{p})$
be the
$\unicode[STIX]{x1D70C}_{x}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{2g}(\overline{\mathbb{Q}}_{p})$
be the
![]() $p$
-adic Galois representation attached to
$p$
-adic Galois representation attached to
![]() $f_{x}$
and let
$f_{x}$
and let
![]() $T_{x}$
be the pseudocharacter defined as the trace of
$T_{x}$
be the pseudocharacter defined as the trace of
![]() $\unicode[STIX]{x1D70C}_{x}$
. When
$\unicode[STIX]{x1D70C}_{x}$
. When
![]() $x$
varies, the traces
$x$
varies, the traces
![]() $T_{x}$
can be interpolated by a pseudocharacter with values in
$T_{x}$
can be interpolated by a pseudocharacter with values in
![]() ${\mathcal{O}}({\mathcal{D}}_{g}^{M})^{\circ }$
. This is stated precisely in the following proposition.
${\mathcal{O}}({\mathcal{D}}_{g}^{M})^{\circ }$
. This is stated precisely in the following proposition.
For every ring
![]() $R$
, we implicitly extend a character of the Hecke algebra
$R$
, we implicitly extend a character of the Hecke algebra
![]() ${\mathcal{H}}_{g}^{M}\rightarrow R^{\times }$
to a morphism of polynomial algebras
${\mathcal{H}}_{g}^{M}\rightarrow R^{\times }$
to a morphism of polynomial algebras
![]() ${\mathcal{H}}_{g}^{M}[X]\rightarrow R[X]$
by applying it to the coefficients. Recall that we fixed an embedding
${\mathcal{H}}_{g}^{M}[X]\rightarrow R[X]$
by applying it to the coefficients. Recall that we fixed an embedding
![]() $G_{\mathbb{Q}_{\ell }}{\hookrightarrow}G_{\mathbb{Q}}$
for every prime
$G_{\mathbb{Q}_{\ell }}{\hookrightarrow}G_{\mathbb{Q}}$
for every prime
![]() $\ell$
, hence an embedding of the inertia subgroup
$\ell$
, hence an embedding of the inertia subgroup
![]() $I_{\ell }$
in
$I_{\ell }$
in
![]() $G_{\mathbb{Q}}$
. As usual
$G_{\mathbb{Q}}$
. As usual
![]() $\operatorname{Frob}_{\ell }$
denotes a lift of the Frobenius at
$\operatorname{Frob}_{\ell }$
denotes a lift of the Frobenius at
![]() $\ell$
to
$\ell$
to
![]() $G_{\mathbb{Q}_{\ell }}$
.
$G_{\mathbb{Q}_{\ell }}$
.
Proposition 2.5. There exists a pseudocharacter
![]() $T_{g}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{D}}_{g}^{M})$
of dimension
$T_{g}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{D}}_{g}^{M})$
of dimension
![]() $2g$
with the following properties:
$2g$
with the following properties:
(i) for every prime
 $\ell$
not dividing
$\ell$
not dividing
 $Np$
and every
$Np$
and every
 $h\in I_{\ell }$
, we have
$h\in I_{\ell }$
, we have
 $T_{g}(h)=2$
, where
$T_{g}(h)=2$
, where
 $2\in {\mathcal{O}}({\mathcal{D}}_{g}^{M})$
denotes the function constantly equal to
$2\in {\mathcal{O}}({\mathcal{D}}_{g}^{M})$
denotes the function constantly equal to
 $2$
;
$2$
;(ii) for every prime
 $\ell$
not dividing
$\ell$
not dividing
 $Np$
, we have
$Np$
, we have
 $P_{\operatorname{char}}(T_{g})(\operatorname{Frob}_{\ell };X)=\unicode[STIX]{x1D713}_{g}(P_{\operatorname{min}}(t_{\ell ,g}^{(g)};X))$
;
$P_{\operatorname{char}}(T_{g})(\operatorname{Frob}_{\ell };X)=\unicode[STIX]{x1D713}_{g}(P_{\operatorname{min}}(t_{\ell ,g}^{(g)};X))$
;(iii) for every
 $x\in S^{\operatorname{cl}}$
, we have
$x\in S^{\operatorname{cl}}$
, we have
 $\operatorname{ev}_{x}\circ \,T_{g}=T_{x}$
.
$\operatorname{ev}_{x}\circ \,T_{g}=T_{x}$
.
Proof. The pseudocharacter
![]() $T_{g}$
is constructed via the interpolation argument of [Reference ChenevierChe04, Proposition 7.1.1]. Its properties are a consequence of those of the classical representations. See [Reference ContiCon16, Theorem 3.5.10] for a detailed proof of the proposition.◻
$T_{g}$
is constructed via the interpolation argument of [Reference ChenevierChe04, Proposition 7.1.1]. Its properties are a consequence of those of the classical representations. See [Reference ContiCon16, Theorem 3.5.10] for a detailed proof of the proposition.◻
Remark 2.6. (i) Let
![]() $x\in {\mathcal{D}}_{g}^{M}(\overline{\mathbb{Q}}_{p})$
. Consider the
$x\in {\mathcal{D}}_{g}^{M}(\overline{\mathbb{Q}}_{p})$
. Consider the
![]() $2g$
-dimensional pseudocharacter
$2g$
-dimensional pseudocharacter
![]() $T_{x}:G_{\mathbb{Q}}\rightarrow \overline{\mathbb{Q}}_{p}$
defined by
$T_{x}:G_{\mathbb{Q}}\rightarrow \overline{\mathbb{Q}}_{p}$
defined by
![]() $T_{x}=\operatorname{ev}_{x}\circ \,T_{g}$
. By a well-known theorem of Taylor (see [Reference TaylorTay91]) there exists a Galois representation
$T_{x}=\operatorname{ev}_{x}\circ \,T_{g}$
. By a well-known theorem of Taylor (see [Reference TaylorTay91]) there exists a Galois representation
![]() $\unicode[STIX]{x1D70C}_{x}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\overline{\mathbb{Q}}_{p})$
satisfying
$\unicode[STIX]{x1D70C}_{x}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\overline{\mathbb{Q}}_{p})$
satisfying
![]() $T_{x}=\operatorname{Tr}(\unicode[STIX]{x1D70C}_{x})$
. We show in §4.2 that, when
$T_{x}=\operatorname{Tr}(\unicode[STIX]{x1D70C}_{x})$
. We show in §4.2 that, when
![]() $\overline{\unicode[STIX]{x1D70C}}_{x}$
is absolutely irreducible,
$\overline{\unicode[STIX]{x1D70C}}_{x}$
is absolutely irreducible,
![]() $\unicode[STIX]{x1D70C}_{x}$
is isomorphic to a representation
$\unicode[STIX]{x1D70C}_{x}$
is isomorphic to a representation
![]() $G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\overline{\mathbb{Q}}_{p})$
.
$G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\overline{\mathbb{Q}}_{p})$
.
(ii) When
![]() $x$
varies in a connected component of
$x$
varies in a connected component of
![]() ${\mathcal{D}}_{g}^{M}$
, the residual representation
${\mathcal{D}}_{g}^{M}$
, the residual representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{x}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{2g}(\overline{\mathbb{Q}}_{p})$
is independent of
$\overline{\unicode[STIX]{x1D70C}}_{x}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{2g}(\overline{\mathbb{Q}}_{p})$
is independent of
![]() $x$
. We call it the residual representation associated with the component.
$x$
. We call it the residual representation associated with the component.
3 Image of Galois representations attached to
 $\operatorname{GSp}_{4}$
-eigenforms
$\operatorname{GSp}_{4}$
-eigenforms
Let
![]() $N$
be a positive integer and let
$N$
be a positive integer and let
![]() $p$
be a prime not dividing
$p$
be a prime not dividing
![]() $N$
. Let
$N$
. Let
![]() $F$
be an overconvergent
$F$
be an overconvergent
![]() $\operatorname{GSp}_{2g}$
-eigenform of level
$\operatorname{GSp}_{2g}$
-eigenform of level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
. Let
$\unicode[STIX]{x1D6E4}_{1}(N)$
. Let
![]() $\unicode[STIX]{x1D70C}_{F,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{2g}(\overline{\mathbb{Q}}_{p})$
be the
$\unicode[STIX]{x1D70C}_{F,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{2g}(\overline{\mathbb{Q}}_{p})$
be the
![]() $p$
-adic Galois representation associated with
$p$
-adic Galois representation associated with
![]() $F$
. It is defined over a
$F$
. It is defined over a
![]() $p$
-adic field
$p$
-adic field
![]() $K$
. Under the technical condition of ‘
$K$
. Under the technical condition of ‘
![]() $\mathbb{Z}_{p}$
-regularity’ of
$\mathbb{Z}_{p}$
-regularity’ of
![]() $\unicode[STIX]{x1D70C}_{F,p}$
and an assumption on the associated residual representation, we prove that the image of
$\unicode[STIX]{x1D70C}_{F,p}$
and an assumption on the associated residual representation, we prove that the image of
![]() $\unicode[STIX]{x1D70C}_{F,p}$
is ‘big’ when
$\unicode[STIX]{x1D70C}_{F,p}$
is ‘big’ when
![]() $g=2$
and
$g=2$
and
![]() $F$
is a classical eigenform that is not a lift of a
$F$
is a classical eigenform that is not a lift of a
![]() $\operatorname{GL}_{2}$
-eigenform (Theorem 3.12). On our way towards this result, we prove a theorem that is needed in §10 (Theorem 3.8).
$\operatorname{GL}_{2}$
-eigenform (Theorem 3.12). On our way towards this result, we prove a theorem that is needed in §10 (Theorem 3.8).
3.1 Trianguline parameters of overconvergent
 $\operatorname{GSp}_{4}$
-eigenforms
$\operatorname{GSp}_{4}$
-eigenforms
We refer to [Reference BergerBer02, Reference ColmezCol08] for the definitions and results that we need from the theory of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules and trianguline representations. Let
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules and trianguline representations. Let
![]() $F$
be as in the beginning of the section. Part (i) of the following theorem is a classical result of Faltings [Reference FaltingsFal89]. Part (ii) is a combination of [Reference KisinKis03, Theorem 6.3] and [Reference ColmezCol08, Proposition 4.3], as Berger observed in [Reference BergerBer11, §4.3].
$F$
be as in the beginning of the section. Part (i) of the following theorem is a classical result of Faltings [Reference FaltingsFal89]. Part (ii) is a combination of [Reference KisinKis03, Theorem 6.3] and [Reference ColmezCol08, Proposition 4.3], as Berger observed in [Reference BergerBer11, §4.3].
Theorem 3.1.
(i) If
 $F$
is a classical eigenform of cohomological weight, then
$F$
is a classical eigenform of cohomological weight, then
 $\unicode[STIX]{x1D70C}_{F,p}|_{G_{\mathbb{Q}_{p}}}$
is crystalline.
$\unicode[STIX]{x1D70C}_{F,p}|_{G_{\mathbb{Q}_{p}}}$
is crystalline.(ii) If
 $g=1$
and the slope of
$g=1$
and the slope of
 $F$
is finite, then
$F$
is finite, then
 $\unicode[STIX]{x1D70C}_{F,p}|_{G_{\mathbb{Q}_{p}}}$
is trianguline.
$\unicode[STIX]{x1D70C}_{F,p}|_{G_{\mathbb{Q}_{p}}}$
is trianguline.
If
![]() $g=2$
, an analogue of Theorem 3.1(ii) for
$g=2$
, an analogue of Theorem 3.1(ii) for
![]() $\unicode[STIX]{x1D70C}_{F,p}$
can be deduced from the work of Kedlaya, Pottharst and Xiao [Reference Kedlaya, Pottharst and XiaoKPX14]. Moreover, the results of [Reference Kedlaya, Pottharst and XiaoKPX14] allow us to write the parameters of the triangulation of
$\unicode[STIX]{x1D70C}_{F,p}$
can be deduced from the work of Kedlaya, Pottharst and Xiao [Reference Kedlaya, Pottharst and XiaoKPX14]. Moreover, the results of [Reference Kedlaya, Pottharst and XiaoKPX14] allow us to write the parameters of the triangulation of
![]() $\unicode[STIX]{x1D70C}_{F,p}$
in terms of a Hecke polynomial, as for classical points. Recall that we are working on an eigenvariety
$\unicode[STIX]{x1D70C}_{F,p}$
in terms of a Hecke polynomial, as for classical points. Recall that we are working on an eigenvariety
![]() ${\mathcal{D}}_{2}^{M}$
with a fixed residual Galois representation
${\mathcal{D}}_{2}^{M}$
with a fixed residual Galois representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
. Suppose that
$\overline{\unicode[STIX]{x1D70C}}$
. Suppose that
![]() $\overline{\unicode[STIX]{x1D70C}}$
is irreducible. By lifting pseudocharacters to representations and considering the associated
$\overline{\unicode[STIX]{x1D70C}}$
is irreducible. By lifting pseudocharacters to representations and considering the associated
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules we can define a family of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules we can define a family of
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules over
![]() ${\mathcal{D}}_{2}^{M}$
in the sense of [Reference Kedlaya, Pottharst and XiaoKPX14, §2.1]. For
${\mathcal{D}}_{2}^{M}$
in the sense of [Reference Kedlaya, Pottharst and XiaoKPX14, §2.1]. For
![]() $x\in {\mathcal{D}}_{2}^{M}(\mathbb{C}_{p})$
, let
$x\in {\mathcal{D}}_{2}^{M}(\mathbb{C}_{p})$
, let
![]() $\unicode[STIX]{x1D70C}_{x}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\overline{\mathbb{Q}}_{p})$
and
$\unicode[STIX]{x1D70C}_{x}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\overline{\mathbb{Q}}_{p})$
and
![]() $\unicode[STIX]{x1D713}_{x}:{\mathcal{H}}_{2}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the Galois representation and the system of Hecke eigenvalues, respectively, attached to
$\unicode[STIX]{x1D713}_{x}:{\mathcal{H}}_{2}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the Galois representation and the system of Hecke eigenvalues, respectively, attached to
![]() $x$
. Let
$x$
. Let
![]() $M_{x}$
be the
$M_{x}$
be the
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module over
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module over
![]() $\overline{\mathbb{Q}}_{p}$
attached to
$\overline{\mathbb{Q}}_{p}$
attached to
![]() $\unicode[STIX]{x1D70C}_{x}$
. Denote by
$\unicode[STIX]{x1D70C}_{x}$
. Denote by
![]() $\operatorname{ev}_{x}$
the evaluation of rigid analytic functions on
$\operatorname{ev}_{x}$
the evaluation of rigid analytic functions on
![]() ${\mathcal{D}}_{2}^{M}$
at
${\mathcal{D}}_{2}^{M}$
at
![]() $x$
. We identify the weight of
$x$
. We identify the weight of
![]() $x$
with a character
$x$
with a character
![]() $(\unicode[STIX]{x1D705}_{1}(x),\unicode[STIX]{x1D705}_{2}(x)):(\mathbb{Z}_{p}^{\times })^{2}\rightarrow \mathbb{C}_{p}^{\times }$
. Let
$(\unicode[STIX]{x1D705}_{1}(x),\unicode[STIX]{x1D705}_{2}(x)):(\mathbb{Z}_{p}^{\times })^{2}\rightarrow \mathbb{C}_{p}^{\times }$
. Let
![]() $\operatorname{id}:\mathbb{Z}_{p}^{\times }\rightarrow \mathbb{Z}_{p}^{\times }$
be the identity. Let
$\operatorname{id}:\mathbb{Z}_{p}^{\times }\rightarrow \mathbb{Z}_{p}^{\times }$
be the identity. Let
![]() $\unicode[STIX]{x1D6FF}_{i}$
,
$\unicode[STIX]{x1D6FF}_{i}$
,
![]() $1\leqslant i\leqslant 4$
be the characters
$1\leqslant i\leqslant 4$
be the characters
![]() $\mathbb{Z}_{p}^{\times }\rightarrow {\mathcal{O}}({\mathcal{D}}_{2}^{M})^{\times }$
defined by
$\mathbb{Z}_{p}^{\times }\rightarrow {\mathcal{O}}({\mathcal{D}}_{2}^{M})^{\times }$
defined by
 $$\begin{eqnarray}\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FF}_{1}|_{\mathbb{Z}_{p}^{\times }}=1,\quad \unicode[STIX]{x1D6FF}_{1}(p)=\unicode[STIX]{x1D713}_{x}(U_{p,2}^{(2)});\quad \unicode[STIX]{x1D6FF}_{2}|_{\mathbb{Z}_{p}^{\times }}=\unicode[STIX]{x1D705}_{1}/\!\operatorname{id},\quad \unicode[STIX]{x1D6FF}_{2}(p)=\unicode[STIX]{x1D713}_{x}((U_{p,2}^{(2)})^{w_{1}});\\ \unicode[STIX]{x1D6FF}_{3}|_{\mathbb{Z}_{p}^{\times }}=\unicode[STIX]{x1D705}_{2}/\!\operatorname{id}^{2},\quad \unicode[STIX]{x1D6FF}_{3}(p)=\unicode[STIX]{x1D713}_{x}((U_{p,2}^{(2)})^{w_{2}});\quad \unicode[STIX]{x1D6FF}_{4}|_{\mathbb{Z}_{p}^{\times }}=\unicode[STIX]{x1D705}_{1}\unicode[STIX]{x1D705}_{2}(p)/\!\operatorname{id}^{3},\quad \unicode[STIX]{x1D6FF}_{4}(p)=\unicode[STIX]{x1D713}_{x}((U_{p,2}^{(2)})^{w_{1}w_{2}}).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}c@{}}\unicode[STIX]{x1D6FF}_{1}|_{\mathbb{Z}_{p}^{\times }}=1,\quad \unicode[STIX]{x1D6FF}_{1}(p)=\unicode[STIX]{x1D713}_{x}(U_{p,2}^{(2)});\quad \unicode[STIX]{x1D6FF}_{2}|_{\mathbb{Z}_{p}^{\times }}=\unicode[STIX]{x1D705}_{1}/\!\operatorname{id},\quad \unicode[STIX]{x1D6FF}_{2}(p)=\unicode[STIX]{x1D713}_{x}((U_{p,2}^{(2)})^{w_{1}});\\ \unicode[STIX]{x1D6FF}_{3}|_{\mathbb{Z}_{p}^{\times }}=\unicode[STIX]{x1D705}_{2}/\!\operatorname{id}^{2},\quad \unicode[STIX]{x1D6FF}_{3}(p)=\unicode[STIX]{x1D713}_{x}((U_{p,2}^{(2)})^{w_{2}});\quad \unicode[STIX]{x1D6FF}_{4}|_{\mathbb{Z}_{p}^{\times }}=\unicode[STIX]{x1D705}_{1}\unicode[STIX]{x1D705}_{2}(p)/\!\operatorname{id}^{3},\quad \unicode[STIX]{x1D6FF}_{4}(p)=\unicode[STIX]{x1D713}_{x}((U_{p,2}^{(2)})^{w_{1}w_{2}}).\end{array}\end{eqnarray}$$
For
![]() $x\in {\mathcal{D}}_{2}^{M}(\mathbb{C}_{p})$
, let
$x\in {\mathcal{D}}_{2}^{M}(\mathbb{C}_{p})$
, let
![]() $\unicode[STIX]{x1D6FF}_{i,x}=\operatorname{ev}_{x}\circ \,\unicode[STIX]{x1D6FF}_{i}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}$
.
$\unicode[STIX]{x1D6FF}_{i,x}=\operatorname{ev}_{x}\circ \,\unicode[STIX]{x1D6FF}_{i}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}$
.
Proposition 3.2.
(i) For every
 $x\in {\mathcal{D}}_{2}^{M}(\mathbb{C}_{p})$
, the
$x\in {\mathcal{D}}_{2}^{M}(\mathbb{C}_{p})$
, the
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
 $M_{x}$
is trianguline.
$M_{x}$
is trianguline.(ii) There exists a Zariski-open rigid analytic subspace
 $\widetilde{{\mathcal{D}}}_{2}^{M}$
of
$\widetilde{{\mathcal{D}}}_{2}^{M}$
of
 ${\mathcal{D}}_{2}^{M}$
such that for every
${\mathcal{D}}_{2}^{M}$
such that for every
 $x\in {\mathcal{D}}_{2}^{M}(\mathbb{C}_{p})$
the
$x\in {\mathcal{D}}_{2}^{M}(\mathbb{C}_{p})$
the
 $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-module
 $M_{x}$
is triangulable with parameters
$M_{x}$
is triangulable with parameters
 $\operatorname{ev}_{x}\circ \,\unicode[STIX]{x1D6FF}_{i}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}$
.
$\operatorname{ev}_{x}\circ \,\unicode[STIX]{x1D6FF}_{i}:\mathbb{Q}_{p}^{\times }\rightarrow \overline{\mathbb{Q}}_{p}$
.
Proof. The first statement follows immediately from [Reference Kedlaya, Pottharst and XiaoKPX14, Corollary 6.3.13]. The second follows from [Reference Kedlaya, Pottharst and XiaoKPX14, Theorem 6.3.10] after checking that the functions
![]() $\unicode[STIX]{x1D6FF}_{i}$
,
$\unicode[STIX]{x1D6FF}_{i}$
,
![]() $1\leqslant i\leqslant 4$
, interpolate the parameters of the triangulations at the classical points. This is true because the parameters of the filtration correspond to the eigenvalues of the crystalline Frobenius at a crystalline point by [Reference ColmezCol08, Proposition 1.8] (that restates a result of Berger), and these are identified with the roots of
$1\leqslant i\leqslant 4$
, interpolate the parameters of the triangulations at the classical points. This is true because the parameters of the filtration correspond to the eigenvalues of the crystalline Frobenius at a crystalline point by [Reference ColmezCol08, Proposition 1.8] (that restates a result of Berger), and these are identified with the roots of
![]() $P_{\operatorname{min}}(U_{p,2}^{(2)})$
by [Reference UrbanUrb05, Théorème 1].◻
$P_{\operatorname{min}}(U_{p,2}^{(2)})$
by [Reference UrbanUrb05, Théorème 1].◻
Now let
![]() $N$
be a positive integer prime to
$N$
be a positive integer prime to
![]() $p$
and let
$p$
and let
![]() $M=N^{3}$
. Let
$M=N^{3}$
. Let
![]() $F$
be an overconvergent
$F$
be an overconvergent
![]() $\operatorname{GSp}_{4}$
-eigenform corresponding to a point of
$\operatorname{GSp}_{4}$
-eigenform corresponding to a point of
![]() $\widetilde{{\mathcal{D}}}_{2}^{M}$
. Suppose that there is a
$\widetilde{{\mathcal{D}}}_{2}^{M}$
. Suppose that there is a
![]() $\operatorname{GL}_{2}$
-eigenform
$\operatorname{GL}_{2}$
-eigenform
![]() $f$
of level
$f$
of level
![]() $N$
such that
$N$
such that
![]() $\unicode[STIX]{x1D70C}_{F,p}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
, with the usual notation. Let
$\unicode[STIX]{x1D70C}_{F,p}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
, with the usual notation. Let
![]() $\unicode[STIX]{x1D712}_{F}:{\mathcal{H}}_{2}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
and
$\unicode[STIX]{x1D712}_{F}:{\mathcal{H}}_{2}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
and
![]() $\unicode[STIX]{x1D712}_{f}:{\mathcal{H}}_{1}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the systems of Hecke eigenvalues of the two forms. For
$\unicode[STIX]{x1D712}_{f}:{\mathcal{H}}_{1}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the systems of Hecke eigenvalues of the two forms. For
![]() $1\leqslant i\leqslant 8$
, define
$1\leqslant i\leqslant 8$
, define
![]() $\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}$
as in Proposition 9.7 by replacing
$\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}$
as in Proposition 9.7 by replacing
![]() $\unicode[STIX]{x1D712}_{1}^{\operatorname{st}}$
by
$\unicode[STIX]{x1D712}_{1}^{\operatorname{st}}$
by
![]() $\unicode[STIX]{x1D712}_{f}$
.
$\unicode[STIX]{x1D712}_{f}$
.
Proposition 3.3. There exists
![]() $i\in \{1,2,\ldots ,8\}$
such that
$i\in \{1,2,\ldots ,8\}$
such that
![]() $\unicode[STIX]{x1D712}_{F}=\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}$
.
$\unicode[STIX]{x1D712}_{F}=\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}$
.
Proof. The proof is completely analogous to that of Proposition 9.7, once we replace
![]() $\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p})$
and
$\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p})$
and
![]() $\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p})$
by the
$\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p})$
by the
![]() $(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6E4})$
-modules
![]() $\mathbf{D}_{\operatorname{rig}}(\unicode[STIX]{x1D70C}_{f,p})$
and
$\mathbf{D}_{\operatorname{rig}}(\unicode[STIX]{x1D70C}_{f,p})$
and
![]() $\mathbf{D}_{\operatorname{rig}}(\unicode[STIX]{x1D70C}_{F,p})$
, respectively, and we use the result of Proposition 3.2.◻
$\mathbf{D}_{\operatorname{rig}}(\unicode[STIX]{x1D70C}_{F,p})$
, respectively, and we use the result of Proposition 3.2.◻
Let
![]() $F$
be a finite slope overconvergent
$F$
be a finite slope overconvergent
![]() $\operatorname{GSp}_{4}$
-eigenform of tame level
$\operatorname{GSp}_{4}$
-eigenform of tame level
![]() $M$
.
$M$
.
Proposition 3.4. There are at most
![]() $2\,\operatorname{dim}_{\overline{\mathbb{Q}}_{p}}\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{F,p})$
points of
$2\,\operatorname{dim}_{\overline{\mathbb{Q}}_{p}}\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{F,p})$
points of
![]() ${\mathcal{D}}_{2}^{M}$
whose associated Galois representation is isomorphic to
${\mathcal{D}}_{2}^{M}$
whose associated Galois representation is isomorphic to
![]() $\unicode[STIX]{x1D70C}_{F,p}$
.
$\unicode[STIX]{x1D70C}_{F,p}$
.
Proof. The accumulation and Zariski-dense set
![]() $Z$
of classical points of
$Z$
of classical points of
![]() ${\mathcal{D}}_{2}^{M}$
satisfies the assumptions (CRYS) and (HT) of [Reference Bellaïche and ChenevierBC09, §3.3.2]. Then [Reference Bellaïche and ChenevierBC09, Theorem 3.3.3] implies that, for every
${\mathcal{D}}_{2}^{M}$
satisfies the assumptions (CRYS) and (HT) of [Reference Bellaïche and ChenevierBC09, §3.3.2]. Then [Reference Bellaïche and ChenevierBC09, Theorem 3.3.3] implies that, for every
![]() $\mathbb{C}_{p}$
-point
$\mathbb{C}_{p}$
-point
![]() $x$
of
$x$
of
![]() ${\mathcal{D}}_{2}^{M}$
,
${\mathcal{D}}_{2}^{M}$
,
![]() $\unicode[STIX]{x1D713}_{x}(U_{p,2}^{(2)})$
is an eigenvalue of the crystalline Frobenius acting on
$\unicode[STIX]{x1D713}_{x}(U_{p,2}^{(2)})$
is an eigenvalue of the crystalline Frobenius acting on
![]() $\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{x})$
. There are exactly two characters of the Iwahori–Hecke algebra giving the same value for
$\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{x})$
. There are exactly two characters of the Iwahori–Hecke algebra giving the same value for
![]() $\unicode[STIX]{x1D713}_{x}(U_{p,2}^{(2)})$
, hence the desired result.◻
$\unicode[STIX]{x1D713}_{x}(U_{p,2}^{(2)})$
, hence the desired result.◻
Now let
![]() $f$
be a finite slope overconvergent
$f$
be a finite slope overconvergent
![]() $\operatorname{GL}_{2}$
-eigenform of tame level
$\operatorname{GL}_{2}$
-eigenform of tame level
![]() $N$
.
$N$
.
Corollary 3.5. There are at most
![]() $2\,\dim _{\overline{\mathbb{Q}}_{p}}\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C})$
points of
$2\,\dim _{\overline{\mathbb{Q}}_{p}}\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C})$
points of
![]() ${\mathcal{D}}_{2}^{M}$
whose associated Galois representation is isomorphic to
${\mathcal{D}}_{2}^{M}$
whose associated Galois representation is isomorphic to
![]() $\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
.
$\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
.
3.2 Representations with symmetric cube of automorphic origin
Let
![]() $V$
be a two-dimensional representation of
$V$
be a two-dimensional representation of
![]() $G_{\mathbb{Q}}$
over a
$G_{\mathbb{Q}}$
over a
![]() $p$
-adic field. We recall a special case of a result of Di Matteo.
$p$
-adic field. We recall a special case of a result of Di Matteo.
Proposition 3.6 [Reference Di MatteoDiM13a, Theorem 2.4.2].
If the representation
![]() $\operatorname{Sym}^{3}V$
is de Rham, then
$\operatorname{Sym}^{3}V$
is de Rham, then
![]() $V$
is the twist by a character of a de Rham representation.
$V$
is the twist by a character of a de Rham representation.
When ‘de Rham’ is replaced by ‘trianguline’, the techniques of [Reference Di MatteoDiM13b] can be modified to prove the following result.
Proposition 3.7. If the representation
![]() $\operatorname{Sym}^{3}V$
is trianguline, then
$\operatorname{Sym}^{3}V$
is trianguline, then
![]() $V$
is either trianguline or the twist by a character of a de Rham representation.
$V$
is either trianguline or the twist by a character of a de Rham representation.
We refer to [Reference ContiCon16, Proposition 3.10.25] for the proof. We only remark here that to obtain triangulinity, rather than potential triangulinity, we need a result of Berger and Chenevier [Reference Berger and ChenevierBC10, Théorème A].
Given a two-dimensional modulo
![]() $p$
representation
$p$
representation
![]() $\overline{\unicode[STIX]{x1D70F}}$
of
$\overline{\unicode[STIX]{x1D70F}}$
of
![]() $G_{\mathbb{Q}}$
, we list here for future reference some assumptions that we need in applying the results of [Reference EmertonEme14]. Here
$G_{\mathbb{Q}}$
, we list here for future reference some assumptions that we need in applying the results of [Reference EmertonEme14]. Here
![]() $\unicode[STIX]{x1D712}$
denotes the modulo
$\unicode[STIX]{x1D712}$
denotes the modulo
![]() $p$
cyclotomic character:
$p$
cyclotomic character:
For convenience we also restate the symmetric cube of the above assumptions, for a four-dimensional modulo
![]() $p$
representation
$p$
representation
![]() $\overline{\unicode[STIX]{x1D70F}}$
of
$\overline{\unicode[STIX]{x1D70F}}$
of
![]() $G_{\mathbb{Q}}$
:
$G_{\mathbb{Q}}$
:
We will always replace the subscript
![]() $\overline{\unicode[STIX]{x1D70F}}$
with the representation we are making the above assumptions on.
$\overline{\unicode[STIX]{x1D70F}}$
with the representation we are making the above assumptions on.
Let
![]() $\unicode[STIX]{x1D70C}_{1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
and
$\unicode[STIX]{x1D70C}_{1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
and
![]() $\unicode[STIX]{x1D70C}_{2}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\overline{\mathbb{Q}}_{p})$
be two continuous representations. We will deduce the following theorem from the two previous propositions.
$\unicode[STIX]{x1D70C}_{2}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\overline{\mathbb{Q}}_{p})$
be two continuous representations. We will deduce the following theorem from the two previous propositions.
Theorem 3.8. Suppose that:
(1)
 $\unicode[STIX]{x1D70C}_{2}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{1}$
;
$\unicode[STIX]{x1D70C}_{2}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{1}$
;(2)
 $\unicode[STIX]{x1D70C}_{2}$
is odd and unramified outside a finite set of primes;
$\unicode[STIX]{x1D70C}_{2}$
is odd and unramified outside a finite set of primes;(3) the residual representation
 $\overline{\unicode[STIX]{x1D70C}}_{1}$
associated with
$\overline{\unicode[STIX]{x1D70C}}_{1}$
associated with
 $\unicode[STIX]{x1D70C}_{1}$
satisfies assumptions
$\unicode[STIX]{x1D70C}_{1}$
satisfies assumptions
 $(\ast _{\overline{\unicode[STIX]{x1D70C}}_{1}})$
.
$(\ast _{\overline{\unicode[STIX]{x1D70C}}_{1}})$
.
Then the following conclusions hold.
(i) If
 $\unicode[STIX]{x1D70C}_{2}$
is associated with an overconvergent cuspidal
$\unicode[STIX]{x1D70C}_{2}$
is associated with an overconvergent cuspidal
 $\operatorname{GSp}_{4}$
-eigenform, then
$\operatorname{GSp}_{4}$
-eigenform, then
 $\unicode[STIX]{x1D70C}_{1}$
is associated with an overconvergent cuspidal
$\unicode[STIX]{x1D70C}_{1}$
is associated with an overconvergent cuspidal
 $\operatorname{GL}_{2}$
-eigenform.
$\operatorname{GL}_{2}$
-eigenform.(ii) If
 $\unicode[STIX]{x1D70C}_{2}$
is associated with a classical cuspidal
$\unicode[STIX]{x1D70C}_{2}$
is associated with a classical cuspidal
 $\operatorname{GSp}_{4}$
-eigenform, then
$\operatorname{GSp}_{4}$
-eigenform, then
 $\unicode[STIX]{x1D70C}_{1}$
is associated with a classical cuspidal
$\unicode[STIX]{x1D70C}_{1}$
is associated with a classical cuspidal
 $\operatorname{GL}_{2}$
-eigenform.
$\operatorname{GL}_{2}$
-eigenform.
Proof. Suppose that
![]() $\unicode[STIX]{x1D70C}_{2}$
is associated with an overconvergent cuspidal
$\unicode[STIX]{x1D70C}_{2}$
is associated with an overconvergent cuspidal
![]() $\operatorname{GSp}_{4}$
-eigenform
$\operatorname{GSp}_{4}$
-eigenform
![]() $F$
. Now
$F$
. Now
![]() $\unicode[STIX]{x1D70C}_{2}$
is trianguline by Proposition 3.2(i), so Proposition 3.7 implies that the representation
$\unicode[STIX]{x1D70C}_{2}$
is trianguline by Proposition 3.2(i), so Proposition 3.7 implies that the representation
![]() $\unicode[STIX]{x1D70C}_{1}$
is either trianguline or the twist by a character of a de Rham representation. Thanks to assumptions (2) and (3) we can apply [Reference EmertonEme14, Theorem 1.2.4(2)] to deduce that
$\unicode[STIX]{x1D70C}_{1}$
is either trianguline or the twist by a character of a de Rham representation. Thanks to assumptions (2) and (3) we can apply [Reference EmertonEme14, Theorem 1.2.4(2)] to deduce that
![]() $\unicode[STIX]{x1D70C}_{1}$
is a twist of a representation associated with a cuspidal overconvergent
$\unicode[STIX]{x1D70C}_{1}$
is a twist of a representation associated with a cuspidal overconvergent
![]() $\operatorname{GL}_{2}$
-eigenform. A study of the Hodge–Tate–Sen weights of
$\operatorname{GL}_{2}$
-eigenform. A study of the Hodge–Tate–Sen weights of
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
shows that the twist occurring here can be taken to be trivial, giving conclusion (i).
$\unicode[STIX]{x1D70C}_{2}$
shows that the twist occurring here can be taken to be trivial, giving conclusion (i).
We prove conclusion (ii). Since
![]() $\unicode[STIX]{x1D70C}_{2}$
is associated with a classical cuspidal
$\unicode[STIX]{x1D70C}_{2}$
is associated with a classical cuspidal
![]() $\operatorname{GSp}_{4}$
-eigenform, it is a de Rham representation. Then Proposition 3.6 implies that
$\operatorname{GSp}_{4}$
-eigenform, it is a de Rham representation. Then Proposition 3.6 implies that
![]() $\unicode[STIX]{x1D70C}_{1}$
is also a de Rham representation up to a twist by a character. As in the previous paragraph, we conclude that
$\unicode[STIX]{x1D70C}_{1}$
is also a de Rham representation up to a twist by a character. As in the previous paragraph, we conclude that
![]() $\unicode[STIX]{x1D70C}_{1}$
is attached to a classical cuspidal
$\unicode[STIX]{x1D70C}_{1}$
is attached to a classical cuspidal
![]() $\operatorname{GL}_{2}$
-eigenform from [Reference EmertonEme14, Theorem 1.2.4(1)] and a study of the Hodge–Tate–Sen weights of
$\operatorname{GL}_{2}$
-eigenform from [Reference EmertonEme14, Theorem 1.2.4(1)] and a study of the Hodge–Tate–Sen weights of
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
.◻
$\unicode[STIX]{x1D70C}_{2}$
.◻
Corollary 3.9. If
![]() $\unicode[STIX]{x1D70C}_{1}$
,
$\unicode[STIX]{x1D70C}_{1}$
,
![]() $\unicode[STIX]{x1D70C}_{2}$
satisfy the assumptions of Theorem 3.8 and
$\unicode[STIX]{x1D70C}_{2}$
satisfy the assumptions of Theorem 3.8 and
![]() $\unicode[STIX]{x1D70C}_{2}$
is associated with a classical cuspidal
$\unicode[STIX]{x1D70C}_{2}$
is associated with a classical cuspidal
![]() $\operatorname{GSp}_{4}$
-eigenform
$\operatorname{GSp}_{4}$
-eigenform
![]() $F$
, then there exists a
$F$
, then there exists a
![]() $\operatorname{GL}_{2}$
-eigenform
$\operatorname{GL}_{2}$
-eigenform
![]() $f$
such that
$f$
such that
![]() $F$
is the symmetric cube lift
$F$
is the symmetric cube lift
![]() $\operatorname{Sym}^{3}f$
given by Corollary 9.2.
$\operatorname{Sym}^{3}f$
given by Corollary 9.2.
Proof. The representation
![]() $\unicode[STIX]{x1D70C}_{1}$
is attached to a classical cuspidal
$\unicode[STIX]{x1D70C}_{1}$
is attached to a classical cuspidal
![]() $\operatorname{GL}_{2}$
-eigenform
$\operatorname{GL}_{2}$
-eigenform
![]() $f$
by Theorem 3.8(ii). Then
$f$
by Theorem 3.8(ii). Then
![]() $\unicode[STIX]{x1D70C}_{2}$
is the
$\unicode[STIX]{x1D70C}_{2}$
is the
![]() $p$
-adic Galois representation attached to the form
$p$
-adic Galois representation attached to the form
![]() $\operatorname{Sym}^{3}f$
. We conclude that
$\operatorname{Sym}^{3}f$
. We conclude that
![]() $F=\operatorname{Sym}^{3}f$
.◻
$F=\operatorname{Sym}^{3}f$
.◻
3.3 A big image result for classical
 $\operatorname{GSp}_{4}$
-eigenforms
$\operatorname{GSp}_{4}$
-eigenforms
In the following definitions, let
![]() $E$
be a finite extension of
$E$
be a finite extension of
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
![]() $R$
be a local ring with maximal ideal
$R$
be a local ring with maximal ideal
![]() $\mathfrak{m}_{R}$
and residue field
$\mathfrak{m}_{R}$
and residue field
![]() $\mathbb{F}$
. Let
$\mathbb{F}$
. Let
![]() $\unicode[STIX]{x1D70F}:G_{E}\rightarrow \operatorname{GSp}_{4}(R)$
be a representation. Let
$\unicode[STIX]{x1D70F}:G_{E}\rightarrow \operatorname{GSp}_{4}(R)$
be a representation. Let
![]() $\operatorname{PGSp}_{4}(R)=\operatorname{GSp}_{4}(R)/R^{\times }$
, where
$\operatorname{PGSp}_{4}(R)=\operatorname{GSp}_{4}(R)/R^{\times }$
, where
![]() $R^{\times }$
is identified with the subgroup of scalar matrices. We denote by
$R^{\times }$
is identified with the subgroup of scalar matrices. We denote by
![]() $\overline{\unicode[STIX]{x1D70F}}:G_{E}\rightarrow \operatorname{GSp}_{4}(\mathbb{F})$
the reduction of
$\overline{\unicode[STIX]{x1D70F}}:G_{E}\rightarrow \operatorname{GSp}_{4}(\mathbb{F})$
the reduction of
![]() $\unicode[STIX]{x1D70F}$
modulo
$\unicode[STIX]{x1D70F}$
modulo
![]() $\mathfrak{m}_{R}$
. Recall that
$\mathfrak{m}_{R}$
. Recall that
![]() $T_{2}$
is the torus consisting of diagonal matrices in
$T_{2}$
is the torus consisting of diagonal matrices in
![]() $\operatorname{GSp}_{4}$
. We give a notion of
$\operatorname{GSp}_{4}$
. We give a notion of
![]() $\mathbb{Z}_{p}$
-regularity of
$\mathbb{Z}_{p}$
-regularity of
![]() $\unicode[STIX]{x1D70F}$
, analogous to that in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, Lemma 4.5(2)].
$\unicode[STIX]{x1D70F}$
, analogous to that in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, Lemma 4.5(2)].
Definition 3.10. We say that
![]() $\unicode[STIX]{x1D70F}$
is
$\unicode[STIX]{x1D70F}$
is
![]() $\mathbb{Z}_{p}$
-regular if there exists
$\mathbb{Z}_{p}$
-regular if there exists
![]() $d\in \operatorname{Im}\unicode[STIX]{x1D70F}\cap T_{2}(\mathbb{Z}_{p})$
with the following property: if
$d\in \operatorname{Im}\unicode[STIX]{x1D70F}\cap T_{2}(\mathbb{Z}_{p})$
with the following property: if
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
are two distinct roots of
$\unicode[STIX]{x1D6FC}^{\prime }$
are two distinct roots of
![]() $\operatorname{GSp}_{4}$
, then
$\operatorname{GSp}_{4}$
, then
![]() $\unicode[STIX]{x1D6FC}(d)\neq \unicode[STIX]{x1D6FC}^{\prime }(d)\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{m}_{R})$
. If
$\unicode[STIX]{x1D6FC}(d)\neq \unicode[STIX]{x1D6FC}^{\prime }(d)\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{m}_{R})$
. If
![]() $d$
has this property we call it a
$d$
has this property we call it a
![]() $\mathbb{Z}_{p}$
-regular element.
$\mathbb{Z}_{p}$
-regular element.
From now on we focus on representations that are either ‘residually full’ or ‘residually of symmetric cube type’, in the sense of the following definition. Note that these two types of representations appear in [Reference PilloniPil12, §5.8] as examples of those for which Pilloni can construct a sequence of Taylor–Wiles primes.
Definition 3.11. We say that
![]() $\unicode[STIX]{x1D70F}$
is:
$\unicode[STIX]{x1D70F}$
is:
(i) residually full if there exists a non-trivial subfield
 $\mathbb{F}^{\prime }$
of
$\mathbb{F}^{\prime }$
of
 $\mathbb{F}$
and an element
$\mathbb{F}$
and an element
 $g\in \operatorname{GSp}_{4}(\mathbb{F})$
such that
$g\in \operatorname{GSp}_{4}(\mathbb{F})$
such that  $$\begin{eqnarray}\operatorname{Sp}_{4}(\mathbb{F}^{\prime })\subset g(\operatorname{Im}\overline{\unicode[STIX]{x1D70F}})g^{-1}\subset \operatorname{GSp}_{4}(\mathbb{F}^{\prime });\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sp}_{4}(\mathbb{F}^{\prime })\subset g(\operatorname{Im}\overline{\unicode[STIX]{x1D70F}})g^{-1}\subset \operatorname{GSp}_{4}(\mathbb{F}^{\prime });\end{eqnarray}$$
(ii) residually of symmetric cube type if there exist a non-trivial subfield
 $\mathbb{F}^{\prime }$
of
$\mathbb{F}^{\prime }$
of
 $\mathbb{F}$
and an element
$\mathbb{F}$
and an element
 $g\in \operatorname{GSp}_{4}(\mathbb{F})$
such that
$g\in \operatorname{GSp}_{4}(\mathbb{F})$
such that  $$\begin{eqnarray}\operatorname{Sym}^{3}\operatorname{SL}_{2}(\mathbb{F}^{\prime })\subset g(\operatorname{Im}\overline{\unicode[STIX]{x1D70F}})g^{-1}\subset \operatorname{Sym}^{3}\operatorname{GL}_{2}(\mathbb{F}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sym}^{3}\operatorname{SL}_{2}(\mathbb{F}^{\prime })\subset g(\operatorname{Im}\overline{\unicode[STIX]{x1D70F}})g^{-1}\subset \operatorname{Sym}^{3}\operatorname{GL}_{2}(\mathbb{F}^{\prime }).\end{eqnarray}$$
We also say that
![]() $\overline{\unicode[STIX]{x1D70F}}$
is full in case (i) and of symmetric cube type in case (ii).
$\overline{\unicode[STIX]{x1D70F}}$
is full in case (i) and of symmetric cube type in case (ii).
We write
![]() $\mathfrak{s}\mathfrak{p}_{4}(K)$
for the Lie algebra of
$\mathfrak{s}\mathfrak{p}_{4}(K)$
for the Lie algebra of
![]() $\operatorname{Sp}_{4}(K)$
and
$\operatorname{Sp}_{4}(K)$
and
![]() $\operatorname{Ad}:\operatorname{GSp}_{4}(K)\rightarrow \operatorname{End}(\mathfrak{s}\mathfrak{p}_{4}(K))$
for the adjoint representation. Let
$\operatorname{Ad}:\operatorname{GSp}_{4}(K)\rightarrow \operatorname{End}(\mathfrak{s}\mathfrak{p}_{4}(K))$
for the adjoint representation. Let
![]() $F$
and
$F$
and
![]() $\unicode[STIX]{x1D70C}_{F,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}({\mathcal{O}}_{K})$
be as in the beginning of the section. Let
$\unicode[STIX]{x1D70C}_{F,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}({\mathcal{O}}_{K})$
be as in the beginning of the section. Let
![]() $E$
be the subfield of
$E$
be the subfield of
![]() $K$
generated over
$K$
generated over
![]() $\mathbb{Q}_{p}$
by the set
$\mathbb{Q}_{p}$
by the set
![]() $\{\operatorname{Tr}(\operatorname{Ad}(\unicode[STIX]{x1D70C}(g)))\}\text{}_{g\in G_{\mathbb{Q}}}$
. Let
$\{\operatorname{Tr}(\operatorname{Ad}(\unicode[STIX]{x1D70C}(g)))\}\text{}_{g\in G_{\mathbb{Q}}}$
. Let
![]() ${\mathcal{O}}_{E}$
be the ring of integers of
${\mathcal{O}}_{E}$
be the ring of integers of
![]() $E$
. For a
$E$
. For a
![]() $\operatorname{GL}_{2}$
-eigenform
$\operatorname{GL}_{2}$
-eigenform
![]() $f$
, we denote by
$f$
, we denote by
![]() $\unicode[STIX]{x1D70C}_{f,p}$
the associated
$\unicode[STIX]{x1D70C}_{f,p}$
the associated
![]() $p$
-adic Galois representation. We will prove the following result.
$p$
-adic Galois representation. We will prove the following result.
Theorem 3.12. Assume that
![]() $\unicode[STIX]{x1D70C}_{F,p}$
is
$\unicode[STIX]{x1D70C}_{F,p}$
is
![]() $\mathbb{Z}_{p}$
-regular and that one of the following two conditions is satisfied:
$\mathbb{Z}_{p}$
-regular and that one of the following two conditions is satisfied:
(i)
 $\unicode[STIX]{x1D70C}_{F,p}$
is residually full;
$\unicode[STIX]{x1D70C}_{F,p}$
is residually full;(ii)
 $F$
is not a
$F$
is not a
 $p$
-stabilization of the symmetric cube lift of a
$p$
-stabilization of the symmetric cube lift of a
 $\operatorname{GL}_{2}$
-eigenform, defined by Corollary 9.2, and
$\operatorname{GL}_{2}$
-eigenform, defined by Corollary 9.2, and
 $\overline{\unicode[STIX]{x1D70C}}_{F,p}$
satisfies the assumptions
$\overline{\unicode[STIX]{x1D70C}}_{F,p}$
satisfies the assumptions
 $(\ast \ast _{\overline{\unicode[STIX]{x1D70C}}_{F,p}})$
.
$(\ast \ast _{\overline{\unicode[STIX]{x1D70C}}_{F,p}})$
.
Then the image of
![]() $\unicode[STIX]{x1D70C}_{F,p}$
contains a principal congruence subgroup of
$\unicode[STIX]{x1D70C}_{F,p}$
contains a principal congruence subgroup of
![]() $\operatorname{Sp}_{4}({\mathcal{O}}_{E})$
.
$\operatorname{Sp}_{4}({\mathcal{O}}_{E})$
.
For use in the proof of Theorem 3.12 we state a result of Pink.
Theorem 3.13 [Reference PinkPin98, Theorem 0.7].
Let
![]() $L$
be a local field and let
$L$
be a local field and let
![]() $H$
be an absolutely simple connected adjoint group over
$H$
be an absolutely simple connected adjoint group over
![]() $L$
. Let
$L$
. Let
![]() $\unicode[STIX]{x1D6E4}$
be a compact Zariski-dense subgroup of
$\unicode[STIX]{x1D6E4}$
be a compact Zariski-dense subgroup of
![]() $H(L)$
. Suppose that the adjoint representation of
$H(L)$
. Suppose that the adjoint representation of
![]() $\unicode[STIX]{x1D6E4}$
is irreducible. Then there exists a closed subfield
$\unicode[STIX]{x1D6E4}$
is irreducible. Then there exists a closed subfield
![]() $E$
of
$E$
of
![]() $L$
and a model
$L$
and a model
![]() $H_{E}$
of
$H_{E}$
of
![]() $H$
over
$H$
over
![]() $E$
such that
$E$
such that
![]() $\unicode[STIX]{x1D6E4}$
is an open subgroup of
$\unicode[STIX]{x1D6E4}$
is an open subgroup of
![]() $H_{E}(E)$
.
$H_{E}(E)$
.
We also need the following lemma, that results from an application of Theorem 5.12. We refer to [Reference ContiCon16, Lemma 3.11.5] for a detailed proof.
Lemma 3.14. Let
![]() ${\mathcal{G}}$
be a profinite group and let
${\mathcal{G}}$
be a profinite group and let
![]() ${\mathcal{G}}_{1}$
be a normal open subgroup of
${\mathcal{G}}_{1}$
be a normal open subgroup of
![]() ${\mathcal{G}}$
. Let
${\mathcal{G}}$
. Let
![]() $L$
be a field. Let
$L$
be a field. Let
![]() $\unicode[STIX]{x1D70F}:{\mathcal{G}}\rightarrow \operatorname{GSp}_{4}(L)$
be a continuous representation. Suppose that:
$\unicode[STIX]{x1D70F}:{\mathcal{G}}\rightarrow \operatorname{GSp}_{4}(L)$
be a continuous representation. Suppose that:
(i) there exists a representation
 $\unicode[STIX]{x1D70F}_{1}^{\prime }:{\mathcal{G}}_{1}\rightarrow \operatorname{GL}_{2}(L)$
such that
$\unicode[STIX]{x1D70F}_{1}^{\prime }:{\mathcal{G}}_{1}\rightarrow \operatorname{GL}_{2}(L)$
such that
 $\unicode[STIX]{x1D70F}|_{{\mathcal{G}}_{1}}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70F}_{1}^{\prime }$
;
$\unicode[STIX]{x1D70F}|_{{\mathcal{G}}_{1}}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70F}_{1}^{\prime }$
;(ii) the image of
 $\unicode[STIX]{x1D70F}_{1}^{\prime }$
contains a principal congruence subgroup of
$\unicode[STIX]{x1D70F}_{1}^{\prime }$
contains a principal congruence subgroup of
 $\operatorname{SL}_{2}(L)$
;
$\operatorname{SL}_{2}(L)$
;(iii) there exists a character
 $\unicode[STIX]{x1D702}:{\mathcal{G}}\rightarrow L^{\times }$
such that
$\unicode[STIX]{x1D702}:{\mathcal{G}}\rightarrow L^{\times }$
such that
 $\det \unicode[STIX]{x1D70F}\cong \unicode[STIX]{x1D702}^{6}$
.
$\det \unicode[STIX]{x1D70F}\cong \unicode[STIX]{x1D702}^{6}$
.
Then there exists a finite extension
![]() $\unicode[STIX]{x1D704}:L{\hookrightarrow}L^{\prime }$
and a representation
$\unicode[STIX]{x1D704}:L{\hookrightarrow}L^{\prime }$
and a representation
![]() $\unicode[STIX]{x1D70F}^{\prime }:{\mathcal{G}}\rightarrow \operatorname{GL}_{2}(L^{\prime })$
such that
$\unicode[STIX]{x1D70F}^{\prime }:{\mathcal{G}}\rightarrow \operatorname{GL}_{2}(L^{\prime })$
such that
![]() $\unicode[STIX]{x1D704}\circ \,\unicode[STIX]{x1D70F}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70F}^{\prime }$
.
$\unicode[STIX]{x1D704}\circ \,\unicode[STIX]{x1D70F}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70F}^{\prime }$
.
The rest of the section is devoted to the proof of Theorem 3.12. Let
![]() $(\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p})^{\prime }$
be the derived subgroup of
$(\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p})^{\prime }$
be the derived subgroup of
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p}$
and let
$\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p}$
and let
![]() $G=(\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p})\cap \operatorname{Sp}_{4}(K)$
. We denote by
$G=(\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p})\cap \operatorname{Sp}_{4}(K)$
. We denote by
![]() $\overline{G}$
the Zariski-closure of
$\overline{G}$
the Zariski-closure of
![]() $G$
in
$G$
in
![]() $\operatorname{Sp}_{4}(K)$
. As in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, §3], we will show first that under the hypotheses of Theorem 3.12 we have
$\operatorname{Sp}_{4}(K)$
. As in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, §3], we will show first that under the hypotheses of Theorem 3.12 we have
![]() $\overline{G}=\operatorname{Sp}_{4}(K)$
, and second that
$\overline{G}=\operatorname{Sp}_{4}(K)$
, and second that
![]() $G$
is
$G$
is
![]() $p$
-adically open in
$p$
-adically open in
![]() $\overline{G}$
. We will replace the ordinarity assumption in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, §3] by that of
$\overline{G}$
. We will replace the ordinarity assumption in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, §3] by that of
![]() $\mathbb{Z}_{p}$
-regularity. Let
$\mathbb{Z}_{p}$
-regularity. Let
![]() $\overline{G}^{\circ }$
denote the connected component of the identity in
$\overline{G}^{\circ }$
denote the connected component of the identity in
![]() $\overline{G}$
.
$\overline{G}$
.
Let
![]() $H$
be any connected, Zariski-closed subgroup of
$H$
be any connected, Zariski-closed subgroup of
![]() $\operatorname{Sp}_{4}$
, defined over
$\operatorname{Sp}_{4}$
, defined over
![]() $K$
. As in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, §3.4], we have six possibilities for the isomorphism class of
$K$
. As in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, §3.4], we have six possibilities for the isomorphism class of
![]() $H$
over
$H$
over
![]() $K$
:
$K$
:
(i)
 $H\cong \operatorname{Sp}_{4}$
;
$H\cong \operatorname{Sp}_{4}$
;(ii)
 $H\cong \operatorname{SL}_{2}\times \operatorname{SL}_{2}$
;
$H\cong \operatorname{SL}_{2}\times \operatorname{SL}_{2}$
;(iii)
 $H\cong \operatorname{SL}_{2}$
embedded in a Klingen parabolic subgroup;
$H\cong \operatorname{SL}_{2}$
embedded in a Klingen parabolic subgroup;(iv)
 $H\cong \operatorname{SL}_{2}$
embedded in a Siegel parabolic subgroup;
$H\cong \operatorname{SL}_{2}$
embedded in a Siegel parabolic subgroup;(v)
 $H\cong \operatorname{SL}_{2}$
embedded via the symmetric cube representation
$H\cong \operatorname{SL}_{2}$
embedded via the symmetric cube representation
 $\operatorname{SL}_{2}\rightarrow \operatorname{Sp}_{4}$
(in this case we write
$\operatorname{SL}_{2}\rightarrow \operatorname{Sp}_{4}$
(in this case we write
 $H\cong \operatorname{Sym}^{3}\operatorname{SL}_{2}$
);
$H\cong \operatorname{Sym}^{3}\operatorname{SL}_{2}$
);(vi)
 $H\cong \{1\}$
.
$H\cong \{1\}$
.
We show that only choice (i) is possible for
![]() $H=\overline{G}^{\circ }$
.
$H=\overline{G}^{\circ }$
.
Lemma 3.15. If condition (i) or (ii) in Theorem 3.12 holds, then
![]() $\overline{G}^{\circ }\cong \operatorname{Sp}_{4}$
.
$\overline{G}^{\circ }\cong \operatorname{Sp}_{4}$
.
Proof. Let
![]() $\mathfrak{m}_{K}$
be the maximal ideal of
$\mathfrak{m}_{K}$
be the maximal ideal of
![]() ${\mathcal{O}}_{K}$
and let
${\mathcal{O}}_{K}$
and let
![]() $\mathbb{F}_{K}={\mathcal{O}}_{K}/\mathfrak{m}_{K}$
. The group
$\mathbb{F}_{K}={\mathcal{O}}_{K}/\mathfrak{m}_{K}$
. The group
![]() $(\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p})^{\prime }$
is contained in
$(\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p})^{\prime }$
is contained in
![]() $\overline{G}^{\circ }({\mathcal{O}}_{K})$
. By reducing modulo
$\overline{G}^{\circ }({\mathcal{O}}_{K})$
. By reducing modulo
![]() $\mathfrak{m}_{K}$
we obtain that the derived subgroup
$\mathfrak{m}_{K}$
we obtain that the derived subgroup
![]() $(\operatorname{Im}\overline{\unicode[STIX]{x1D70C}}_{F,p})^{\prime }$
of
$(\operatorname{Im}\overline{\unicode[STIX]{x1D70C}}_{F,p})^{\prime }$
of
![]() $\operatorname{Im}\overline{\unicode[STIX]{x1D70C}}_{F,p}$
is contained in
$\operatorname{Im}\overline{\unicode[STIX]{x1D70C}}_{F,p}$
is contained in
![]() $\overline{G}^{\circ }(\mathbb{F}_{K})$
. If
$\overline{G}^{\circ }(\mathbb{F}_{K})$
. If
![]() $\unicode[STIX]{x1D70C}_{F,p}$
is residually full, then the only choice for the isomorphism class of
$\unicode[STIX]{x1D70C}_{F,p}$
is residually full, then the only choice for the isomorphism class of
![]() $\overline{G}^{\circ }$
is
$\overline{G}^{\circ }$
is
![]() $\overline{G}^{\circ }\cong \operatorname{Sp}_{4}$
. If
$\overline{G}^{\circ }\cong \operatorname{Sp}_{4}$
. If
![]() $\unicode[STIX]{x1D70C}_{F,p}$
is residually of symmetric cube type, then either
$\unicode[STIX]{x1D70C}_{F,p}$
is residually of symmetric cube type, then either
![]() $\overline{G}^{\circ }\cong \operatorname{Sp}_{4}$
or
$\overline{G}^{\circ }\cong \operatorname{Sp}_{4}$
or
![]() $\overline{G}^{\circ }\cong \operatorname{Sym}^{3}\operatorname{SL}_{2}$
.
$\overline{G}^{\circ }\cong \operatorname{Sym}^{3}\operatorname{SL}_{2}$
.
Suppose that
![]() $\overline{G}^{\circ }\cong \operatorname{Sym}^{3}\operatorname{SL}_{2}$
. We show that there exists a
$\overline{G}^{\circ }\cong \operatorname{Sym}^{3}\operatorname{SL}_{2}$
. We show that there exists a
![]() $\operatorname{GL}_{2}$
-eigenform
$\operatorname{GL}_{2}$
-eigenform
![]() $f$
such that
$f$
such that
![]() $\unicode[STIX]{x1D70C}_{F,p}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
. This will contradict the second part of condition (ii) of Theorem 3.12, concluding the proof of Lemma 3.15. As
$\unicode[STIX]{x1D70C}_{F,p}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
. This will contradict the second part of condition (ii) of Theorem 3.12, concluding the proof of Lemma 3.15. As
![]() $\overline{G}^{\circ }(K)$
is of finite index in
$\overline{G}^{\circ }(K)$
is of finite index in
![]() $\overline{G}(K)$
, Lemma 3.14 implies that
$\overline{G}(K)$
, Lemma 3.14 implies that
![]() $\overline{G}(K)\subset \operatorname{Sym}^{3}\operatorname{SL}_{2}(K)$
, so
$\overline{G}(K)\subset \operatorname{Sym}^{3}\operatorname{SL}_{2}(K)$
, so
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p}\subset \operatorname{Sym}^{3}\operatorname{GL}_{2}(K)$
. Hence, there exists a representation
$\operatorname{Im}\unicode[STIX]{x1D70C}_{F,p}\subset \operatorname{Sym}^{3}\operatorname{GL}_{2}(K)$
. Hence, there exists a representation
![]() $\unicode[STIX]{x1D70C}^{\prime }$
satisfying
$\unicode[STIX]{x1D70C}^{\prime }$
satisfying
![]() $\unicode[STIX]{x1D70C}_{F,p}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}^{\prime }$
. As
$\unicode[STIX]{x1D70C}_{F,p}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}^{\prime }$
. As
![]() $\unicode[STIX]{x1D70C}_{F,p}$
is associated with a
$\unicode[STIX]{x1D70C}_{F,p}$
is associated with a
![]() $\operatorname{GSp}_{4}$
-eigenform, Corollary 3.9 implies that
$\operatorname{GSp}_{4}$
-eigenform, Corollary 3.9 implies that
![]() $\unicode[STIX]{x1D70C}^{\prime }$
is associated with a
$\unicode[STIX]{x1D70C}^{\prime }$
is associated with a
![]() $\operatorname{GL}_{2}$
-eigenform
$\operatorname{GL}_{2}$
-eigenform
![]() $f$
.◻
$f$
.◻
We equip all groups with their
![]() $p$
-adic topology. The proof of Theorem 3.12 is completed by the following proposition.
$p$
-adic topology. The proof of Theorem 3.12 is completed by the following proposition.
Proposition 3.16. Suppose that
![]() $\overline{G}\cong \operatorname{Sp}_{4}(K)$
. Then the group
$\overline{G}\cong \operatorname{Sp}_{4}(K)$
. Then the group
![]() $G$
contains an open subgroup of
$G$
contains an open subgroup of
![]() $\operatorname{Sp}_{4}(E)$
.
$\operatorname{Sp}_{4}(E)$
.
Proof. Consider the image
![]() $G^{\operatorname{ad}}$
of
$G^{\operatorname{ad}}$
of
![]() $G$
under the projection
$G$
under the projection
![]() $\operatorname{Sp}_{4}(K)\rightarrow \operatorname{PGSp}_{4}(K)$
. It is a compact subgroup of
$\operatorname{Sp}_{4}(K)\rightarrow \operatorname{PGSp}_{4}(K)$
. It is a compact subgroup of
![]() $\operatorname{PGSp}_{4}(K)$
. Since
$\operatorname{PGSp}_{4}(K)$
. Since
![]() $\overline{G}\cong \operatorname{Sp}_{4}(K)$
, the group
$\overline{G}\cong \operatorname{Sp}_{4}(K)$
, the group
![]() $G^{\operatorname{ad}}$
is Zariski-dense in
$G^{\operatorname{ad}}$
is Zariski-dense in
![]() $\operatorname{PGSp}_{4}(K)$
. By Theorem 3.13 there is a model
$\operatorname{PGSp}_{4}(K)$
. By Theorem 3.13 there is a model
![]() $H$
of
$H$
of
![]() $\operatorname{PGSp}_{4}$
over
$\operatorname{PGSp}_{4}$
over
![]() $E$
such that
$E$
such that
![]() $G^{\operatorname{ad}}$
is an open subgroup of
$G^{\operatorname{ad}}$
is an open subgroup of
![]() $H(E)$
. By the assumption of
$H(E)$
. By the assumption of
![]() $\mathbb{Z}_{p}$
-regularity of
$\mathbb{Z}_{p}$
-regularity of
![]() $\unicode[STIX]{x1D70C}$
, there is a diagonal element
$\unicode[STIX]{x1D70C}$
, there is a diagonal element
![]() $d$
with pairwise distinct eigenvalues. The group
$d$
with pairwise distinct eigenvalues. The group
![]() $H(E)$
must contain the centralizer of
$H(E)$
must contain the centralizer of
![]() $d$
in
$d$
in
![]() $\operatorname{PGSp}_{4}(E)$
, which is a split torus in
$\operatorname{PGSp}_{4}(E)$
, which is a split torus in
![]() $\operatorname{PGSp}_{4}(E)$
. As
$\operatorname{PGSp}_{4}(E)$
. As
![]() $H$
is split and
$H$
is split and
![]() $H\times _{E}K\cong \operatorname{PGSp}_{4/K}$
,
$H\times _{E}K\cong \operatorname{PGSp}_{4/K}$
,
![]() $H$
is a split form of
$H$
is a split form of
![]() $\operatorname{PGSp}_{4}$
over
$\operatorname{PGSp}_{4}$
over
![]() $E$
. Then
$E$
. Then
![]() $H$
must be isomorphic to
$H$
must be isomorphic to
![]() $\operatorname{PGSp}_{4}$
over
$\operatorname{PGSp}_{4}$
over
![]() $E$
by unicity of the quasi-split form of a reductive group. Hence,
$E$
by unicity of the quasi-split form of a reductive group. Hence,
![]() $G^{\operatorname{ad}}$
is an open subgroup of
$G^{\operatorname{ad}}$
is an open subgroup of
![]() $\operatorname{PGSp}_{4}(E)$
. As the map
$\operatorname{PGSp}_{4}(E)$
. As the map
![]() $\operatorname{Sp}_{4}(K)\rightarrow \operatorname{PGSp}_{4}(K)$
has degree
$\operatorname{Sp}_{4}(K)\rightarrow \operatorname{PGSp}_{4}(K)$
has degree
![]() $2$
and
$2$
and
![]() $G\cap \operatorname{Sp}_{4}(E)$
surjects onto
$G\cap \operatorname{Sp}_{4}(E)$
surjects onto
![]() $G^{\operatorname{ad}}\cap \operatorname{PGSp}_{4}(E)$
,
$G^{\operatorname{ad}}\cap \operatorname{PGSp}_{4}(E)$
,
![]() $G$
must contain an open subgroup of
$G$
must contain an open subgroup of
![]() $\operatorname{Sp}_{4}(E)$
. In particular,
$\operatorname{Sp}_{4}(E)$
. In particular,
![]() $G$
contains a principal congruence subgroup of
$G$
contains a principal congruence subgroup of
![]() $\operatorname{Sp}_{4}({\mathcal{O}}_{E})$
.◻
$\operatorname{Sp}_{4}({\mathcal{O}}_{E})$
.◻
Theorem 3.12 states that, when
![]() $\overline{\unicode[STIX]{x1D70C}}_{F,p}$
is either full or of symmetric cube type, the image of
$\overline{\unicode[STIX]{x1D70C}}_{F,p}$
is either full or of symmetric cube type, the image of
![]() $\unicode[STIX]{x1D70C}_{F,p}$
is large if and only if
$\unicode[STIX]{x1D70C}_{F,p}$
is large if and only if
![]() $F$
is not a lift of an eigenform from a smaller group, the only possible such lift under these assumptions being associated with the symmetric cube representation of
$F$
is not a lift of an eigenform from a smaller group, the only possible such lift under these assumptions being associated with the symmetric cube representation of
![]() $\operatorname{GL}_{2}$
. We think that a similar result should hold under more general assumptions on the residual representation, and that it would follow from Pink’s theorem together with an analogue of Corollary 3.9 for the other possible Langlands lifts to
$\operatorname{GL}_{2}$
. We think that a similar result should hold under more general assumptions on the residual representation, and that it would follow from Pink’s theorem together with an analogue of Corollary 3.9 for the other possible Langlands lifts to
![]() $\operatorname{GSp}_{4}$
.
$\operatorname{GSp}_{4}$
.
4 Finite slope families of
 $\operatorname{GSp}_{2g}$
-eigenforms
$\operatorname{GSp}_{2g}$
-eigenforms
In this section, we define families of finite slope
![]() $\operatorname{GSp}_{2g}$
-eigenforms of level
$\operatorname{GSp}_{2g}$
-eigenforms of level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)\,\cap \,\unicode[STIX]{x1D6E4}_{0}(p)$
, extending the definitions given in [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, §3.1] for
$\unicode[STIX]{x1D6E4}_{1}(N)\,\cap \,\unicode[STIX]{x1D6E4}_{0}(p)$
, extending the definitions given in [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, §3.1] for
![]() $g=1$
. Our goal is to define such families integrally. In the following sections, we only use families of genus
$g=1$
. Our goal is to define such families integrally. In the following sections, we only use families of genus
![]() $1$
or
$1$
or
![]() $2$
, but we can give the definitions for general genus with no extra effort.
$2$
, but we can give the definitions for general genus with no extra effort.
Let
![]() $p$
be a prime number and let
$p$
be a prime number and let
![]() $N$
be a positive integer prime to
$N$
be a positive integer prime to
![]() $p$
. For
$p$
. For
![]() $g\geqslant 1$
let
$g\geqslant 1$
let
![]() ${\mathcal{D}}_{g}^{N,h}$
be the
${\mathcal{D}}_{g}^{N,h}$
be the
![]() $\operatorname{GSp}_{2g}$
-eigenvariety of tame level
$\operatorname{GSp}_{2g}$
-eigenvariety of tame level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
. Let
$\unicode[STIX]{x1D6E4}_{1}(N)$
. Let
![]() $h\in \mathbb{Q}^{+,\times }$
. As the slope
$h\in \mathbb{Q}^{+,\times }$
. As the slope
![]() $\operatorname{sl}:{\mathcal{D}}_{g}^{N}(\mathbb{C}_{p})\rightarrow \mathbb{R}^{{\geqslant}0}$
is the valuation of a rigid analytic function on
$\operatorname{sl}:{\mathcal{D}}_{g}^{N}(\mathbb{C}_{p})\rightarrow \mathbb{R}^{{\geqslant}0}$
is the valuation of a rigid analytic function on
![]() ${\mathcal{D}}_{g}^{N}$
, the locus of
${\mathcal{D}}_{g}^{N}$
, the locus of
![]() $\mathbb{C}_{p}$
-points
$\mathbb{C}_{p}$
-points
![]() $x\in {\mathcal{D}}_{g}^{N}$
satisfying
$x\in {\mathcal{D}}_{g}^{N}$
satisfying
![]() $\operatorname{sl}(x)\leqslant h$
admits a structure of rigid analytic subvariety of
$\operatorname{sl}(x)\leqslant h$
admits a structure of rigid analytic subvariety of
![]() ${\mathcal{D}}_{g}^{N}$
. We denote it by
${\mathcal{D}}_{g}^{N}$
. We denote it by
![]() ${\mathcal{D}}_{g}^{N,h}$
. We write
${\mathcal{D}}_{g}^{N,h}$
. We write
![]() $w_{g}^{h}$
for the restriction of the weight map to
$w_{g}^{h}$
for the restriction of the weight map to
![]() ${\mathcal{D}}_{g}^{N,h}$
. Recall that we always identify the
${\mathcal{D}}_{g}^{N,h}$
. Recall that we always identify the
![]() $g$
-dimensional weight space
$g$
-dimensional weight space
![]() ${\mathcal{W}}_{g}$
with a disjoint union of open discs of centre
${\mathcal{W}}_{g}$
with a disjoint union of open discs of centre
![]() $0$
and radius
$0$
and radius
![]() $1$
. A standard way to obtain an integral structure on an admissible domain of an eigenvariety is to pull back the integral structure on the weight space via the weight map. The restriction of the weight map to
$1$
. A standard way to obtain an integral structure on an admissible domain of an eigenvariety is to pull back the integral structure on the weight space via the weight map. The restriction of the weight map to
![]() ${\mathcal{D}}_{g}^{N,h}$
is not, in general, finite if
${\mathcal{D}}_{g}^{N,h}$
is not, in general, finite if
![]() $h>0$
, but it becomes finite when restricted to a sufficiently small admissible domain in
$h>0$
, but it becomes finite when restricted to a sufficiently small admissible domain in
![]() ${\mathcal{D}}_{g}^{N,h}$
. This is assured by a result of Bellaïche that we recall in the following proposition. For every affinoid subdomain
${\mathcal{D}}_{g}^{N,h}$
. This is assured by a result of Bellaïche that we recall in the following proposition. For every affinoid subdomain
![]() $V$
of
$V$
of
![]() ${\mathcal{W}}_{g}^{\circ }$
, let
${\mathcal{W}}_{g}^{\circ }$
, let
![]() ${\mathcal{D}}_{g,V}^{N,h}={\mathcal{D}}_{g}^{N,h}\times _{{\mathcal{W}}_{g}^{\circ }}V$
and let
${\mathcal{D}}_{g,V}^{N,h}={\mathcal{D}}_{g}^{N,h}\times _{{\mathcal{W}}_{g}^{\circ }}V$
and let
![]() $w_{g,V}^{h}=w_{g}^{h}|_{{\mathcal{D}}_{g,V}^{N,h}}:{\mathcal{D}}_{g,V}^{N,h}\rightarrow V$
.
$w_{g,V}^{h}=w_{g}^{h}|_{{\mathcal{D}}_{g,V}^{N,h}}:{\mathcal{D}}_{g,V}^{N,h}\rightarrow V$
.
Proposition 4.1 (Bellaïche [Reference BellaïcheBel12]).
(i) For every
 $\unicode[STIX]{x1D705}\in {\mathcal{W}}_{g}^{\circ }(\overline{\mathbb{Q}}_{p})$
there exists an affinoid neighborhood
$\unicode[STIX]{x1D705}\in {\mathcal{W}}_{g}^{\circ }(\overline{\mathbb{Q}}_{p})$
there exists an affinoid neighborhood
 $V_{h,\unicode[STIX]{x1D705}}$
of
$V_{h,\unicode[STIX]{x1D705}}$
of
 $\unicode[STIX]{x1D705}$
in
$\unicode[STIX]{x1D705}$
in
 ${\mathcal{W}}_{g}^{\circ }$
such that the map
${\mathcal{W}}_{g}^{\circ }$
such that the map
 $w_{g,V_{h,\unicode[STIX]{x1D705}}}^{h}$
is finite.
$w_{g,V_{h,\unicode[STIX]{x1D705}}}^{h}$
is finite.(ii) When
 $h$
varies in
$h$
varies in
 $\mathbb{Q}^{+,\times }$
and
$\mathbb{Q}^{+,\times }$
and
 $\unicode[STIX]{x1D705}$
varies in
$\unicode[STIX]{x1D705}$
varies in
 ${\mathcal{W}}_{g}^{\circ }$
, the set
${\mathcal{W}}_{g}^{\circ }$
, the set
 $\{(w_{g,V_{h,\unicode[STIX]{x1D705}}}^{h})^{-1}(V_{h,\unicode[STIX]{x1D705}})\}\text{}_{h,\unicode[STIX]{x1D705}}$
is an admissible affinoid covering of
$\{(w_{g,V_{h,\unicode[STIX]{x1D705}}}^{h})^{-1}(V_{h,\unicode[STIX]{x1D705}})\}\text{}_{h,\unicode[STIX]{x1D705}}$
is an admissible affinoid covering of
 ${\mathcal{D}}_{g}^{N}$
.
${\mathcal{D}}_{g}^{N}$
.
In Bellaïche’s terminology, a pair
![]() $(V_{h,\unicode[STIX]{x1D705}},h)$
such that
$(V_{h,\unicode[STIX]{x1D705}},h)$
such that
![]() $V_{h,\unicode[STIX]{x1D705}}$
has the property described in part (i) is called an adapted pair. Part (i) of Proposition 4.1 follows from the fact that the characteristic power series of
$V_{h,\unicode[STIX]{x1D705}}$
has the property described in part (i) is called an adapted pair. Part (i) of Proposition 4.1 follows from the fact that the characteristic power series of
![]() $U_{p}^{(2)}$
acting on modules of overconvergent eigenforms is strictly convergent, in particular from the calculation in [Reference BellaïcheBel12, Proposition II.1.12] and the fact that the map from the eigenvariety to the spectral variety is finite. Part (ii) follows from part (i) together with the admissibility of Buzzard’s covering of the spectral variety [Reference BuzzardBuz07, Theorem 4.6] and the construction of the eigenvariety (see [Reference BellaïcheBel12, Theorem II.3.3]).
$U_{p}^{(2)}$
acting on modules of overconvergent eigenforms is strictly convergent, in particular from the calculation in [Reference BellaïcheBel12, Proposition II.1.12] and the fact that the map from the eigenvariety to the spectral variety is finite. Part (ii) follows from part (i) together with the admissibility of Buzzard’s covering of the spectral variety [Reference BuzzardBuz07, Theorem 4.6] and the construction of the eigenvariety (see [Reference BellaïcheBel12, Theorem II.3.3]).
Remark 4.2. (i) By Proposition 4.1 there exists a radius
![]() $r_{h,\unicode[STIX]{x1D705}}\in p^{\mathbb{Q}}$
such that
$r_{h,\unicode[STIX]{x1D705}}\in p^{\mathbb{Q}}$
such that
is a finite morphism. By the results of Hida theory for
![]() $\operatorname{GSp}_{2g}$
, we can take
$\operatorname{GSp}_{2g}$
, we can take
![]() $r_{0,\unicode[STIX]{x1D705}}=1$
for every
$r_{0,\unicode[STIX]{x1D705}}=1$
for every
![]() $\unicode[STIX]{x1D705}$
.
$\unicode[STIX]{x1D705}$
.
(ii) We would like to have an estimate for
![]() $r_{h,\unicode[STIX]{x1D705}}$
independent of
$r_{h,\unicode[STIX]{x1D705}}$
independent of
![]() $\unicode[STIX]{x1D705}$
and with the property that
$\unicode[STIX]{x1D705}$
and with the property that
![]() $r_{h,\unicode[STIX]{x1D705}}\rightarrow 1$
for
$r_{h,\unicode[STIX]{x1D705}}\rightarrow 1$
for
![]() $h\rightarrow 0$
, to recover the ordinary case in this limit. This is not available at the moment for the group
$h\rightarrow 0$
, to recover the ordinary case in this limit. This is not available at the moment for the group
![]() $\operatorname{GSp}_{2g}$
. An estimate of the analogue of this radius is known for the eigenvarieties associated with unitary groups compact at infinity by the work of Chenevier [Reference ChenevierChe04, Théorème 5.3.1].
$\operatorname{GSp}_{2g}$
. An estimate of the analogue of this radius is known for the eigenvarieties associated with unitary groups compact at infinity by the work of Chenevier [Reference ChenevierChe04, Théorème 5.3.1].
4.1 Families defined over
 $\mathbb{Z}_{p}$
$\mathbb{Z}_{p}$
For our purpose of studying the images of Galois representations, we will need to have our finite slope families defined over
![]() $\mathbb{Z}_{p}$
. For this reason we specialize to families over weight discs for which we can construct a
$\mathbb{Z}_{p}$
. For this reason we specialize to families over weight discs for which we can construct a
![]() $\mathbb{Z}_{p}$
-model. For simplicity we only work on the connected component
$\mathbb{Z}_{p}$
-model. For simplicity we only work on the connected component
![]() ${\mathcal{W}}_{g}^{\circ }$
. Recall that we defined coordinates
${\mathcal{W}}_{g}^{\circ }$
. Recall that we defined coordinates
![]() $T_{1},T_{2},\ldots ,T_{g}$
on
$T_{1},T_{2},\ldots ,T_{g}$
on
![]() ${\mathcal{W}}_{g}^{\circ }$
. Let
${\mathcal{W}}_{g}^{\circ }$
. Let
![]() $\unicode[STIX]{x1D705}$
be a point of
$\unicode[STIX]{x1D705}$
be a point of
![]() ${\mathcal{W}}_{g}^{\circ }$
with coordinates
${\mathcal{W}}_{g}^{\circ }$
with coordinates
![]() $(\unicode[STIX]{x1D705}_{1},\unicode[STIX]{x1D705}_{2},\ldots ,\unicode[STIX]{x1D705}_{g})$
in
$(\unicode[STIX]{x1D705}_{1},\unicode[STIX]{x1D705}_{2},\ldots ,\unicode[STIX]{x1D705}_{g})$
in
![]() $\mathbb{Z}_{p}^{g}$
; for instance, we can take as
$\mathbb{Z}_{p}^{g}$
; for instance, we can take as
![]() $\unicode[STIX]{x1D705}$
the arithmetic prime
$\unicode[STIX]{x1D705}$
the arithmetic prime
![]() $P_{\text{}\underline{k}}$
for some
$P_{\text{}\underline{k}}$
for some
![]() $\text{}\underline{k}\in \mathbb{Z}^{g}$
. Let
$\text{}\underline{k}\in \mathbb{Z}^{g}$
. Let
![]() $r_{h,\unicode[STIX]{x1D705}}$
be the largest radius in
$r_{h,\unicode[STIX]{x1D705}}$
be the largest radius in
![]() $p^{\mathbb{Q}}$
such that the map
$p^{\mathbb{Q}}$
such that the map
![]() $w_{\unicode[STIX]{x1D705},B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})}:{\mathcal{D}}_{g,B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})}^{N,h}\rightarrow B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})$
is finite. Such a radius is non-zero thanks to Remark 4.2(i). Let
$w_{\unicode[STIX]{x1D705},B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})}:{\mathcal{D}}_{g,B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})}^{N,h}\rightarrow B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})$
is finite. Such a radius is non-zero thanks to Remark 4.2(i). Let
![]() $s_{h}$
be a rational number satisfying
$s_{h}$
be a rational number satisfying
![]() $r_{h}=p^{s_{h}}$
. We define a model for
$r_{h}=p^{s_{h}}$
. We define a model for
![]() $B_{g}(\unicode[STIX]{x1D705},r_{h}^{-})$
over
$B_{g}(\unicode[STIX]{x1D705},r_{h}^{-})$
over
![]() $\mathbb{Q}_{p}$
by adapting Berthelot’s construction for the wide open unit disc (see [Reference de JongdeJ95, §7]). Write
$\mathbb{Q}_{p}$
by adapting Berthelot’s construction for the wide open unit disc (see [Reference de JongdeJ95, §7]). Write
![]() $s_{h}=b/a$
for some
$s_{h}=b/a$
for some
![]() $a,b\in \mathbb{N}$
. For
$a,b\in \mathbb{N}$
. For
![]() $i\geqslant 1$
, let
$i\geqslant 1$
, let
![]() $s_{i}=s_{h}+1/2^{i}$
and
$s_{i}=s_{h}+1/2^{i}$
and
![]() $r_{i}=p^{-s_{i}}$
. Set
$r_{i}=p^{-s_{i}}$
. Set
and
![]() $A_{r_{i}}=A_{r_{i}}^{\circ }[p^{-1}]$
. Set
$A_{r_{i}}=A_{r_{i}}^{\circ }[p^{-1}]$
. Set
![]() $B_{i}=\operatorname{Spm}A_{r_{i}}$
. Then
$B_{i}=\operatorname{Spm}A_{r_{i}}$
. Then
![]() $B_{i}$
is a
$B_{i}$
is a
![]() $\mathbb{Q}_{p}$
-model of the disc of centre
$\mathbb{Q}_{p}$
-model of the disc of centre
![]() $\unicode[STIX]{x1D705}$
and radius
$\unicode[STIX]{x1D705}$
and radius
![]() $r_{i}$
. We define morphisms
$r_{i}$
. We define morphisms
![]() $A_{r_{i+1}}^{\circ }\rightarrow A_{r_{i}}^{\circ }$
by
$A_{r_{i+1}}^{\circ }\rightarrow A_{r_{i}}^{\circ }$
by
They induce compact maps
![]() $A_{r_{i+1}}\rightarrow A_{r_{i}}$
which give open immersions
$A_{r_{i+1}}\rightarrow A_{r_{i}}$
which give open immersions
![]() $B_{i}{\hookrightarrow}B_{i+1}$
. We define
$B_{i}{\hookrightarrow}B_{i+1}$
. We define
![]() $B_{g,h}=\mathop{\varinjlim }\nolimits_{i}B_{i}$
where the limit is taken with respect to the above immersions. Let
$B_{g,h}=\mathop{\varinjlim }\nolimits_{i}B_{i}$
where the limit is taken with respect to the above immersions. Let
![]() $\unicode[STIX]{x1D6EC}_{g,h}={\mathcal{O}}(B_{g,h})^{\circ }$
. Then
$\unicode[STIX]{x1D6EC}_{g,h}={\mathcal{O}}(B_{g,h})^{\circ }$
. Then
![]() $\unicode[STIX]{x1D6EC}_{g,h}=\mathop{\varprojlim }\nolimits_{i}{\mathcal{O}}(\operatorname{Spm}B_{i})^{\circ }=\mathop{\varprojlim }\nolimits_{i}A_{r_{i}}^{\circ }$
. We call
$\unicode[STIX]{x1D6EC}_{g,h}=\mathop{\varprojlim }\nolimits_{i}{\mathcal{O}}(\operatorname{Spm}B_{i})^{\circ }=\mathop{\varprojlim }\nolimits_{i}A_{r_{i}}^{\circ }$
. We call
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
the genus
$\unicode[STIX]{x1D6EC}_{g,h}$
the genus
![]() $g$
,
$g$
,
![]() $h$
-adapted Iwasawa algebra; we leave its dependence on
$h$
-adapted Iwasawa algebra; we leave its dependence on
![]() $\unicode[STIX]{x1D705}$
implicit. We define
$\unicode[STIX]{x1D705}$
implicit. We define
![]() $t_{1},t_{2},\ldots ,t_{g}\in \unicode[STIX]{x1D6EC}_{g,h}$
as the projective limits of the variables
$t_{1},t_{2},\ldots ,t_{g}\in \unicode[STIX]{x1D6EC}_{g,h}$
as the projective limits of the variables
![]() $t_{1},t_{2},\ldots ,t_{g}$
, respectively, of
$t_{1},t_{2},\ldots ,t_{g}$
, respectively, of
![]() $A_{r_{i}}^{\circ }$
.
$A_{r_{i}}^{\circ }$
.
There is a map of
![]() $\mathbb{Z}_{p}$
-algebras
$\mathbb{Z}_{p}$
-algebras
![]() $\unicode[STIX]{x1D704}_{g,h}^{\ast }:\unicode[STIX]{x1D6EC}_{g}\rightarrow \unicode[STIX]{x1D6EC}_{g,h}$
defined by
$\unicode[STIX]{x1D704}_{g,h}^{\ast }:\unicode[STIX]{x1D6EC}_{g}\rightarrow \unicode[STIX]{x1D6EC}_{g,h}$
defined by
![]() $T_{j}\mapsto t_{j}+\unicode[STIX]{x1D705}_{j}$
for
$T_{j}\mapsto t_{j}+\unicode[STIX]{x1D705}_{j}$
for
![]() $j=1,2,\ldots ,g$
. The inclusion
$j=1,2,\ldots ,g$
. The inclusion
![]() $\unicode[STIX]{x1D704}_{g,h}:B_{g,h}{\hookrightarrow}{\mathcal{W}}_{g}^{\circ }$
induced by
$\unicode[STIX]{x1D704}_{g,h}:B_{g,h}{\hookrightarrow}{\mathcal{W}}_{g}^{\circ }$
induced by
![]() $\unicode[STIX]{x1D704}_{g,h}^{\ast }$
makes
$\unicode[STIX]{x1D704}_{g,h}^{\ast }$
makes
![]() $B_{g,h}$
into a
$B_{g,h}$
into a
![]() $\mathbb{Q}_{p}$
-model of
$\mathbb{Q}_{p}$
-model of
![]() $B_{g}(\unicode[STIX]{x1D705},r_{h}^{-})$
, endowed with the integral structure defined by
$B_{g}(\unicode[STIX]{x1D705},r_{h}^{-})$
, endowed with the integral structure defined by
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
.
$\unicode[STIX]{x1D6EC}_{g,h}$
.
Let
![]() $\unicode[STIX]{x1D702}_{h}$
be an element of
$\unicode[STIX]{x1D702}_{h}$
be an element of
![]() $\overline{\mathbb{Q}}_{p}$
satisfying
$\overline{\mathbb{Q}}_{p}$
satisfying
![]() $v_{p}(\unicode[STIX]{x1D702}_{h})=s_{h}$
. Let
$v_{p}(\unicode[STIX]{x1D702}_{h})=s_{h}$
. Let
![]() $K_{h}=\mathbb{Q}_{p}(\unicode[STIX]{x1D702}_{h})$
and let
$K_{h}=\mathbb{Q}_{p}(\unicode[STIX]{x1D702}_{h})$
and let
![]() ${\mathcal{O}}_{h}$
be the ring of integers of
${\mathcal{O}}_{h}$
be the ring of integers of
![]() $K_{h}$
. The algebra
$K_{h}$
. The algebra
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
is not a ring of formal series over
$\unicode[STIX]{x1D6EC}_{g,h}$
is not a ring of formal series over
![]() $\mathbb{Z}_{p}$
, but there is an isomorphism
$\mathbb{Z}_{p}$
, but there is an isomorphism
![]() $\unicode[STIX]{x1D6EC}_{g,h}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}_{h}\cong {\mathcal{O}}_{h}[[t_{1},t_{2},\ldots ,t_{g}]]$
.
$\unicode[STIX]{x1D6EC}_{g,h}\otimes _{\mathbb{Z}_{p}}{\mathcal{O}}_{h}\cong {\mathcal{O}}_{h}[[t_{1},t_{2},\ldots ,t_{g}]]$
.
We say that a prime of
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
is arithmetic if it lies over an arithmetic prime of
$\unicode[STIX]{x1D6EC}_{g,h}$
is arithmetic if it lies over an arithmetic prime of
![]() $\unicode[STIX]{x1D6EC}_{g}$
. By an abuse of notation we will write again
$\unicode[STIX]{x1D6EC}_{g}$
. By an abuse of notation we will write again
![]() $P_{\text{}\underline{k}}$
for an arithmetic prime of
$P_{\text{}\underline{k}}$
for an arithmetic prime of
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
lying over the arithmetic prime
$\unicode[STIX]{x1D6EC}_{g,h}$
lying over the arithmetic prime
![]() $P_{\text{}\underline{k}}$
of
$P_{\text{}\underline{k}}$
of
![]() $\unicode[STIX]{x1D6EC}_{g}$
.
$\unicode[STIX]{x1D6EC}_{g}$
.
Remark 4.3. Let
![]() $\text{}\underline{k}=(k_{1},k_{2},\ldots ,k_{g})$
be a cohomological weight for
$\text{}\underline{k}=(k_{1},k_{2},\ldots ,k_{g})$
be a cohomological weight for
![]() $\operatorname{GSp}_{2g}$
. There exists a prime
$\operatorname{GSp}_{2g}$
. There exists a prime
![]() $\mathfrak{P}$
of
$\mathfrak{P}$
of
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
lying over the prime
$\unicode[STIX]{x1D6EC}_{g,h}$
lying over the prime
![]() $P_{\text{}\underline{k}}$
of
$P_{\text{}\underline{k}}$
of
![]() $\unicode[STIX]{x1D6EC}_{g}$
if and only if the classical weight
$\unicode[STIX]{x1D6EC}_{g}$
if and only if the classical weight
![]() $\text{}\underline{k}$
belongs to the disc
$\text{}\underline{k}$
belongs to the disc
![]() $B_{g}(0,r_{h}^{-})$
; otherwise, we have
$B_{g}(0,r_{h}^{-})$
; otherwise, we have
![]() $P_{\text{}\underline{k}}\unicode[STIX]{x1D6EC}_{g}=\unicode[STIX]{x1D6EC}_{g}$
. This happens if and only if
$P_{\text{}\underline{k}}\unicode[STIX]{x1D6EC}_{g}=\unicode[STIX]{x1D6EC}_{g}$
. This happens if and only if
![]() $v_{p}(k_{i})>-v_{p}(r_{h})-1$
for
$v_{p}(k_{i})>-v_{p}(r_{h})-1$
for
![]() $i=1,2,\ldots ,g$
, as we can see via a simple calculation.
$i=1,2,\ldots ,g$
, as we can see via a simple calculation.
Let
![]() ${\mathcal{D}}_{g,h}^{N}$
be the rigid analytic space fitting in the following Cartesian diagram.
${\mathcal{D}}_{g,h}^{N}$
be the rigid analytic space fitting in the following Cartesian diagram.

The rigid analytic space
![]() ${\mathcal{D}}_{g,h}^{N}$
is a model of
${\mathcal{D}}_{g,h}^{N}$
is a model of
![]() ${\mathcal{D}}_{g,B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})}^{N,h}$
over a
${\mathcal{D}}_{g,B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})}^{N,h}$
over a
![]() $p$
-adic field, but it is not necessarily defined over
$p$
-adic field, but it is not necessarily defined over
![]() $\mathbb{Q}_{p}$
since the map
$\mathbb{Q}_{p}$
since the map
![]() $\unicode[STIX]{x1D704}_{g,h}$
may not be. We say that a
$\unicode[STIX]{x1D704}_{g,h}$
may not be. We say that a
![]() $\mathbb{C}_{p}$
-point of
$\mathbb{C}_{p}$
-point of
![]() ${\mathcal{D}}_{g,h}^{N}$
is classical if it is a classical point of
${\mathcal{D}}_{g,h}^{N}$
is classical if it is a classical point of
![]() ${\mathcal{D}}_{g,B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})}^{N,h}$
.
${\mathcal{D}}_{g,B_{g}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}}^{-})}^{N,h}$
.
Let
![]() $\mathbb{T}_{g,h}={\mathcal{O}}({\mathcal{D}}_{g,h}^{N})^{\circ }$
. We call
$\mathbb{T}_{g,h}={\mathcal{O}}({\mathcal{D}}_{g,h}^{N})^{\circ }$
. We call
![]() $\mathbb{T}_{g,h}$
the genus
$\mathbb{T}_{g,h}$
the genus
![]() $g$
,
$g$
,
![]() $h$
-adapted Hecke algebra; we leave its dependence on
$h$
-adapted Hecke algebra; we leave its dependence on
![]() $\unicode[STIX]{x1D705}$
implicit again. The weight map induces a morphism
$\unicode[STIX]{x1D705}$
implicit again. The weight map induces a morphism
![]() $w_{g,h}:{\mathcal{D}}_{g,h}^{N}\rightarrow B_{g,h}$
, hence a morphism
$w_{g,h}:{\mathcal{D}}_{g,h}^{N}\rightarrow B_{g,h}$
, hence a morphism
![]() $w_{g,h}^{\ast }:\unicode[STIX]{x1D6EC}_{g,h}\rightarrow \mathbb{T}_{g,h}$
. Thanks to our choice of
$w_{g,h}^{\ast }:\unicode[STIX]{x1D6EC}_{g,h}\rightarrow \mathbb{T}_{g,h}$
. Thanks to our choice of
![]() $r_{h}$
,
$r_{h}$
,
![]() $w_{g,h}^{\ast }$
gives
$w_{g,h}^{\ast }$
gives
![]() $\mathbb{T}_{g,h}$
a structure of finite
$\mathbb{T}_{g,h}$
a structure of finite
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
-algebra. The
$\unicode[STIX]{x1D6EC}_{g,h}$
-algebra. The
![]() ${\mathcal{D}}_{g,h}^{N}\rightarrow {\mathcal{D}}_{g}^{N,h}$
appearing in the diagram induces a map
${\mathcal{D}}_{g,h}^{N}\rightarrow {\mathcal{D}}_{g}^{N,h}$
appearing in the diagram induces a map
![]() ${\mathcal{O}}({\mathcal{D}}_{g}^{N,h})^{\circ }\rightarrow \mathbb{T}_{g,h}$
, that we compose with
${\mathcal{O}}({\mathcal{D}}_{g}^{N,h})^{\circ }\rightarrow \mathbb{T}_{g,h}$
, that we compose with
![]() $\unicode[STIX]{x1D713}_{g}:{\mathcal{H}}_{g}^{N}\rightarrow {\mathcal{O}}({\mathcal{D}}_{g}^{N,h})^{\circ }$
to obtain a morphism
$\unicode[STIX]{x1D713}_{g}:{\mathcal{H}}_{g}^{N}\rightarrow {\mathcal{O}}({\mathcal{D}}_{g}^{N,h})^{\circ }$
to obtain a morphism
![]() $\unicode[STIX]{x1D713}_{g,h}:{\mathcal{H}}_{g}^{N}\rightarrow \mathbb{T}_{g,h}$
.
$\unicode[STIX]{x1D713}_{g,h}:{\mathcal{H}}_{g}^{N}\rightarrow \mathbb{T}_{g,h}$
.
For a prime
![]() $\mathfrak{P}$
of
$\mathfrak{P}$
of
![]() $\mathbb{T}_{g,h}$
, we denote by
$\mathbb{T}_{g,h}$
, we denote by
![]() $\operatorname{ev}_{\mathfrak{P}}:\mathbb{T}_{g,h}\rightarrow \overline{\mathbb{Z}}_{p}$
the evaluation at
$\operatorname{ev}_{\mathfrak{P}}:\mathbb{T}_{g,h}\rightarrow \overline{\mathbb{Z}}_{p}$
the evaluation at
![]() $\mathfrak{P}$
. We say that
$\mathfrak{P}$
. We say that
![]() $\mathfrak{P}$
is a classical point of
$\mathfrak{P}$
is a classical point of
![]() $\operatorname{Spec}\mathbb{T}_{g,h}$
if
$\operatorname{Spec}\mathbb{T}_{g,h}$
if
![]() $\operatorname{ev}_{\mathfrak{P}}\circ \,\unicode[STIX]{x1D713}_{g,h}:{\mathcal{H}}_{g}^{N}\rightarrow \overline{\mathbb{Z}}_{p}$
is the system of Hecke eigenvalues attached to a classical
$\operatorname{ev}_{\mathfrak{P}}\circ \,\unicode[STIX]{x1D713}_{g,h}:{\mathcal{H}}_{g}^{N}\rightarrow \overline{\mathbb{Z}}_{p}$
is the system of Hecke eigenvalues attached to a classical
![]() $\operatorname{GSp}_{2g}$
-eigenform. These systems of eigenvalues also appear at classical points of
$\operatorname{GSp}_{2g}$
-eigenform. These systems of eigenvalues also appear at classical points of
![]() ${\mathcal{D}}_{g,h}^{N}$
.
${\mathcal{D}}_{g,h}^{N}$
.
Definition 4.4. We call the family of
![]() $\operatorname{GSp}_{2g}$
-eigenforms of slope bounded by
$\operatorname{GSp}_{2g}$
-eigenforms of slope bounded by
![]() $h$
an irreducible component
$h$
an irreducible component
![]() $I$
of
$I$
of
![]() ${\mathcal{D}}_{g,h}^{N}$
, equipped with the integral structure defined by
${\mathcal{D}}_{g,h}^{N}$
, equipped with the integral structure defined by
![]() $\mathbb{T}_{g,h}$
.
$\mathbb{T}_{g,h}$
.
We will usually refer to an
![]() $I$
as in Definition 4.4 simply as a finite slope family. Let
$I$
as in Definition 4.4 simply as a finite slope family. Let
![]() $\mathbb{I}^{\circ }={\mathcal{O}}(I)$
. Then
$\mathbb{I}^{\circ }={\mathcal{O}}(I)$
. Then
![]() $\mathbb{I}^{\circ }$
is a finite
$\mathbb{I}^{\circ }$
is a finite
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
-algebra that is also profinite and local. The component
$\unicode[STIX]{x1D6EC}_{g,h}$
-algebra that is also profinite and local. The component
![]() $I$
is determined by the surjective morphism
$I$
is determined by the surjective morphism
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{g,h}{\twoheadrightarrow}\mathbb{I}^{\circ }$
. We sometimes refer to
$\unicode[STIX]{x1D703}:\mathbb{T}_{g,h}{\twoheadrightarrow}\mathbb{I}^{\circ }$
. We sometimes refer to
![]() $\unicode[STIX]{x1D703}$
as a finite slope family. The family
$\unicode[STIX]{x1D703}$
as a finite slope family. The family
![]() $I$
is equipped with maps
$I$
is equipped with maps
![]() $w_{\unicode[STIX]{x1D703}}:I\rightarrow B_{g,h}$
and
$w_{\unicode[STIX]{x1D703}}:I\rightarrow B_{g,h}$
and
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D703}}:{\mathcal{H}}_{g}^{N}\rightarrow \mathbb{I}^{\circ }$
induced by
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D703}}:{\mathcal{H}}_{g}^{N}\rightarrow \mathbb{I}^{\circ }$
induced by
![]() $w_{g,h}$
and
$w_{g,h}$
and
![]() $\unicode[STIX]{x1D713}_{g,h}$
, respectively. Here
$\unicode[STIX]{x1D713}_{g,h}$
, respectively. Here
![]() $^{\circ }$
denotes the fact that we are working with integral objects. When introducing relative Sen theory in §7, we will need to invert
$^{\circ }$
denotes the fact that we are working with integral objects. When introducing relative Sen theory in §7, we will need to invert
![]() $p$
and we will drop the
$p$
and we will drop the
![]() $^{\circ }$
from all rings.
$^{\circ }$
from all rings.
Proposition 2.2 implies that every family
![]() $I$
contains at least a classical point. By the accumulation property of classical point and the irreducibility of
$I$
contains at least a classical point. By the accumulation property of classical point and the irreducibility of
![]() $I$
, the classical points are a Zariski-dense subset of
$I$
, the classical points are a Zariski-dense subset of
![]() $I$
. Hence, the set of classical points of
$I$
. Hence, the set of classical points of
![]() $\operatorname{Spec}\mathbb{I}^{\circ }$
is Zariski-dense in
$\operatorname{Spec}\mathbb{I}^{\circ }$
is Zariski-dense in
![]() $\operatorname{Spec}\mathbb{I}^{\circ }$
. Every classical point of
$\operatorname{Spec}\mathbb{I}^{\circ }$
. Every classical point of
![]() $\operatorname{Spec}\mathbb{I}^{\circ }$
lies over an arithmetic prime of
$\operatorname{Spec}\mathbb{I}^{\circ }$
lies over an arithmetic prime of
![]() $\operatorname{Spec}\unicode[STIX]{x1D6EC}_{g,h}$
. For a family
$\operatorname{Spec}\unicode[STIX]{x1D6EC}_{g,h}$
. For a family
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{g,h}\rightarrow \mathbb{I}^{\circ }$
, we give the following.
$\unicode[STIX]{x1D703}:\mathbb{T}_{g,h}\rightarrow \mathbb{I}^{\circ }$
, we give the following.
Definition 4.5. We call an arithmetic prime
![]() $P_{\text{}\underline{k}}\subset \unicode[STIX]{x1D6EC}_{g,h}$
non-critical for
$P_{\text{}\underline{k}}\subset \unicode[STIX]{x1D6EC}_{g,h}$
non-critical for
![]() $\mathbb{I}^{\circ }$
if:
$\mathbb{I}^{\circ }$
if:
(i) every point of
 $\operatorname{Spec}\mathbb{I}^{\circ }$
lying over
$\operatorname{Spec}\mathbb{I}^{\circ }$
lying over
 $P_{\text{}\underline{k}}$
is classical;
$P_{\text{}\underline{k}}$
is classical;(ii) the map
 $w_{g,B_{g,h}}^{\ast }:\unicode[STIX]{x1D6EC}_{g,h}\rightarrow \mathbb{I}^{\circ }$
is étale at every point of
$w_{g,B_{g,h}}^{\ast }:\unicode[STIX]{x1D6EC}_{g,h}\rightarrow \mathbb{I}^{\circ }$
is étale at every point of
 $\operatorname{Spec}\mathbb{I}^{\circ }$
lying over
$\operatorname{Spec}\mathbb{I}^{\circ }$
lying over
 $P_{\text{}\underline{k}}$
.
$P_{\text{}\underline{k}}$
.
We call
![]() $P_{\text{}\underline{k}}$
critical for
$P_{\text{}\underline{k}}$
critical for
![]() $\mathbb{I}^{\circ }$
if it is not non-critical. We also say that a classical weight
$\mathbb{I}^{\circ }$
if it is not non-critical. We also say that a classical weight
![]() $\text{}\underline{k}$
is critical or non-critical for
$\text{}\underline{k}$
is critical or non-critical for
![]() $\mathbb{I}^{\circ }$
if the arithmetic prime
$\mathbb{I}^{\circ }$
if the arithmetic prime
![]() $P_{\text{}\underline{k}}$
has that property.
$P_{\text{}\underline{k}}$
has that property.
Remark 4.6. (i) By Proposition 2.2, if
![]() $\text{}\underline{k}$
is a classical weight belonging to
$\text{}\underline{k}$
is a classical weight belonging to
![]() $B_{g,h}$
and
$B_{g,h}$
and
![]() $h<k_{g}-g(g+1)/2$
then
$h<k_{g}-g(g+1)/2$
then
![]() $\text{}\underline{k}$
satisfies condition (i) of Definition 4.5. We do not know of a simple assumption on the weight that guarantees that the second condition is also satisfied.
$\text{}\underline{k}$
satisfies condition (i) of Definition 4.5. We do not know of a simple assumption on the weight that guarantees that the second condition is also satisfied.
(ii) The set of non-critical arithmetic primes is Zariski-dense in
![]() $\unicode[STIX]{x1D6EC}_{g,h}$
. This follows from part (i) of the remark and the fact that the locus of étaleness of the morphism
$\unicode[STIX]{x1D6EC}_{g,h}$
. This follows from part (i) of the remark and the fact that the locus of étaleness of the morphism
![]() $\unicode[STIX]{x1D6EC}_{g,h}\rightarrow \mathbb{I}^{\circ }$
is Zariski-open in
$\unicode[STIX]{x1D6EC}_{g,h}\rightarrow \mathbb{I}^{\circ }$
is Zariski-open in
![]() $\mathbb{I}^{\circ }$
.
$\mathbb{I}^{\circ }$
.
4.2 The Galois representation associated with a finite slope family
Let
![]() $\unicode[STIX]{x1D705}$
be a point of
$\unicode[STIX]{x1D705}$
be a point of
![]() ${\mathcal{W}}_{g}^{\circ }$
with
${\mathcal{W}}_{g}^{\circ }$
with
![]() $\mathbb{Z}_{p}$
-coordinates. Let
$\mathbb{Z}_{p}$
-coordinates. Let
![]() $\mathbb{T}_{2,h}$
be the genus
$\mathbb{T}_{2,h}$
be the genus
![]() $2$
,
$2$
,
![]() $h$
-adapted Hecke algebra of centre
$h$
-adapted Hecke algebra of centre
![]() $\unicode[STIX]{x1D705}$
. As before, we will leave the dependence on
$\unicode[STIX]{x1D705}$
. As before, we will leave the dependence on
![]() $\unicode[STIX]{x1D705}$
implicit. For simplicity, let
$\unicode[STIX]{x1D705}$
implicit. For simplicity, let
![]() $\unicode[STIX]{x1D6EC}_{h}=\unicode[STIX]{x1D6EC}_{2,h}$
,
$\unicode[STIX]{x1D6EC}_{h}=\unicode[STIX]{x1D6EC}_{2,h}$
,
![]() $\mathbb{T}_{h}=\mathbb{T}_{2,h}$
. We implicitly replace
$\mathbb{T}_{h}=\mathbb{T}_{2,h}$
. We implicitly replace
![]() $\mathbb{T}_{h}$
by one of its local components. Let
$\mathbb{T}_{h}$
by one of its local components. Let
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a finite slope family of
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a finite slope family of
![]() $\operatorname{GSp}_{4}$
-eigenforms. Let
$\operatorname{GSp}_{4}$
-eigenforms. Let
![]() $\mathbb{F}_{\mathbb{T}_{h}}$
be the residue field of
$\mathbb{F}_{\mathbb{T}_{h}}$
be the residue field of
![]() $\mathbb{T}_{h}$
. The pseudocharacter
$\mathbb{T}_{h}$
. The pseudocharacter
![]() $T_{2}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{D}}_{2}^{N})^{\circ }$
induces pseudocharacters
$T_{2}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{D}}_{2}^{N})^{\circ }$
induces pseudocharacters
![]() $T_{\mathbb{T}_{h}}:G_{\mathbb{Q}}\rightarrow \mathbb{T}_{h}$
and
$T_{\mathbb{T}_{h}}:G_{\mathbb{Q}}\rightarrow \mathbb{T}_{h}$
and
![]() $\overline{T}_{\mathbb{T}_{h}}:G_{\mathbb{Q}}\rightarrow \mathbb{F}_{\mathbb{T}_{h}}$
. By [Reference RouquierRou96, Corollary 5.2] the pseudocharacter
$\overline{T}_{\mathbb{T}_{h}}:G_{\mathbb{Q}}\rightarrow \mathbb{F}_{\mathbb{T}_{h}}$
. By [Reference RouquierRou96, Corollary 5.2] the pseudocharacter
![]() $\overline{T}_{\mathbb{T}_{h}}$
is associated with a representation
$\overline{T}_{\mathbb{T}_{h}}$
is associated with a representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}_{h}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\overline{\mathbb{F}}_{p})$
, unique up to isomorphism. We call
$\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}_{h}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\overline{\mathbb{F}}_{p})$
, unique up to isomorphism. We call
![]() $\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}_{h}}$
the residual Galois representation associated with
$\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}_{h}}$
the residual Galois representation associated with
![]() $\mathbb{T}_{h}$
. We assume from now on that
$\mathbb{T}_{h}$
. We assume from now on that
By the compactness of
![]() $G_{\mathbb{Q}}$
there exists a finite extension
$G_{\mathbb{Q}}$
there exists a finite extension
![]() $\mathbb{F}^{\prime }$
of
$\mathbb{F}^{\prime }$
of
![]() $\mathbb{F}_{\mathbb{T}_{h}}$
such that
$\mathbb{F}_{\mathbb{T}_{h}}$
such that
![]() $\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}_{h}}$
is defined on
$\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}_{h}}$
is defined on
![]() $\mathbb{F}^{\prime }$
. Let
$\mathbb{F}^{\prime }$
. Let
![]() $W(\mathbb{F}_{\mathbb{T}_{h}})$
and
$W(\mathbb{F}_{\mathbb{T}_{h}})$
and
![]() $W(\mathbb{F}^{\prime })$
be the rings of Witt vectors of
$W(\mathbb{F}^{\prime })$
be the rings of Witt vectors of
![]() $\mathbb{F}_{\mathbb{T}_{h}}$
and
$\mathbb{F}_{\mathbb{T}_{h}}$
and
![]() $\mathbb{F}^{\prime }$
, respectively. Let
$\mathbb{F}^{\prime }$
, respectively. Let
![]() $\mathbb{T}_{h}^{\prime }=\mathbb{T}_{h}\otimes _{W(\mathbb{F}_{\mathbb{T}_{h}})}W(\mathbb{F}^{\prime })$
. We consider
$\mathbb{T}_{h}^{\prime }=\mathbb{T}_{h}\otimes _{W(\mathbb{F}_{\mathbb{T}_{h}})}W(\mathbb{F}^{\prime })$
. We consider
![]() $T_{\mathbb{T}_{h}}$
as a pseudocharacter
$T_{\mathbb{T}_{h}}$
as a pseudocharacter
![]() $G_{\mathbb{Q}}\rightarrow \mathbb{T}_{h}^{\prime }$
via the natural inclusion
$G_{\mathbb{Q}}\rightarrow \mathbb{T}_{h}^{\prime }$
via the natural inclusion
![]() $\mathbb{T}_{h}{\hookrightarrow}\mathbb{T}_{h}^{\prime }$
. Then
$\mathbb{T}_{h}{\hookrightarrow}\mathbb{T}_{h}^{\prime }$
. Then
![]() $T_{\mathbb{T}_{h}}$
satisfies the hypotheses of [Reference RouquierRou96, Corollary 5.2], so there exists a representation
$T_{\mathbb{T}_{h}}$
satisfies the hypotheses of [Reference RouquierRou96, Corollary 5.2], so there exists a representation
![]() $\unicode[STIX]{x1D70C}_{\mathbb{T}_{h}^{\prime }}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\mathbb{T}_{h}^{\prime })$
such that
$\unicode[STIX]{x1D70C}_{\mathbb{T}_{h}^{\prime }}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\mathbb{T}_{h}^{\prime })$
such that
![]() $\operatorname{Tr}\unicode[STIX]{x1D70C}_{T_{h}^{\prime }}=\mathbb{T}_{\mathbb{T}_{h}}$
. By Proposition 2.5, for every prime
$\operatorname{Tr}\unicode[STIX]{x1D70C}_{T_{h}^{\prime }}=\mathbb{T}_{\mathbb{T}_{h}}$
. By Proposition 2.5, for every prime
![]() $\ell$
not dividing
$\ell$
not dividing
![]() $Np$
we have
$Np$
we have
In particular,
![]() $\operatorname{Tr}(T_{\mathbb{T}_{h}})(\operatorname{Frob}_{\ell })$
is an element of
$\operatorname{Tr}(T_{\mathbb{T}_{h}})(\operatorname{Frob}_{\ell })$
is an element of
![]() $\mathbb{T}_{h}$
. As
$\mathbb{T}_{h}$
. As
![]() $\mathbb{T}_{h}$
is complete, Chebotarev’s theorem implies that
$\mathbb{T}_{h}$
is complete, Chebotarev’s theorem implies that
![]() $T_{\mathbb{T}_{h}}(g)$
is an element of
$T_{\mathbb{T}_{h}}(g)$
is an element of
![]() $\mathbb{T}_{h}$
for every
$\mathbb{T}_{h}$
for every
![]() $g\in G_{\mathbb{Q}}$
. By a theorem of Carayol [Reference CarayolCar94, Théorème 1] there exists a representation
$g\in G_{\mathbb{Q}}$
. By a theorem of Carayol [Reference CarayolCar94, Théorème 1] there exists a representation
![]() $\unicode[STIX]{x1D70C}_{\mathbb{T}_{h}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\mathbb{T}_{h})$
that is isomorphic to
$\unicode[STIX]{x1D70C}_{\mathbb{T}_{h}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\mathbb{T}_{h})$
that is isomorphic to
![]() $\unicode[STIX]{x1D70C}_{\mathbb{T}_{h}}$
over
$\unicode[STIX]{x1D70C}_{\mathbb{T}_{h}}$
over
![]() $\mathbb{T}_{h}^{\prime }$
.
$\mathbb{T}_{h}^{\prime }$
.
The morphism
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
induces a morphism
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
induces a morphism
![]() $\operatorname{GL}_{4}(\mathbb{T}_{h})\rightarrow \operatorname{GL}_{4}(\mathbb{I}^{\circ })$
that we still denote by
$\operatorname{GL}_{4}(\mathbb{T}_{h})\rightarrow \operatorname{GL}_{4}(\mathbb{I}^{\circ })$
that we still denote by
![]() $\unicode[STIX]{x1D703}$
. Let
$\unicode[STIX]{x1D703}$
. Let
![]() $\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\mathbb{I}^{\circ })$
be the representation defined by
$\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\mathbb{I}^{\circ })$
be the representation defined by
![]() $\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}=\unicode[STIX]{x1D703}\circ \,\unicode[STIX]{x1D70C}_{\mathbb{T}_{h}}$
. Recall that we set
$\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}=\unicode[STIX]{x1D703}\circ \,\unicode[STIX]{x1D70C}_{\mathbb{T}_{h}}$
. Recall that we set
![]() $\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D713}_{2}|_{{\mathcal{D}}_{2,B_{h}}^{M,h}}):{\mathcal{H}}_{2}^{M}\rightarrow \mathbb{I}^{\circ }$
. Let
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D703}}=\unicode[STIX]{x1D703}(\unicode[STIX]{x1D713}_{2}|_{{\mathcal{D}}_{2,B_{h}}^{M,h}}):{\mathcal{H}}_{2}^{M}\rightarrow \mathbb{I}^{\circ }$
. Let
As
![]() $\unicode[STIX]{x1D6EC}_{h}\subset \mathbb{I}_{\operatorname{Tr}}^{\circ }\subset \mathbb{I}^{\circ }$
, the ring
$\unicode[STIX]{x1D6EC}_{h}\subset \mathbb{I}_{\operatorname{Tr}}^{\circ }\subset \mathbb{I}^{\circ }$
, the ring
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is a finite
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is a finite
![]() $\unicode[STIX]{x1D6EC}_{h}$
-algebra. In particular,
$\unicode[STIX]{x1D6EC}_{h}$
-algebra. In particular,
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is complete. We keep our usual notation for the reduction modulo an ideal
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is complete. We keep our usual notation for the reduction modulo an ideal
![]() $\mathfrak{P}$
of
$\mathfrak{P}$
of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
. We say that a point
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
. We say that a point
![]() $\mathfrak{P}$
of
$\mathfrak{P}$
of
![]() $\operatorname{Spec}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is classical if it lies under a classical point of
$\operatorname{Spec}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is classical if it lies under a classical point of
![]() $\operatorname{Spec}\mathbb{I}^{\circ }$
.
$\operatorname{Spec}\mathbb{I}^{\circ }$
.
By Proposition 2.5 we have
![]() $P_{\operatorname{char}}(\operatorname{Tr}(\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}))(\operatorname{Frob}_{\ell })=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D703}}(P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X))$
, so we deduce that
$P_{\operatorname{char}}(\operatorname{Tr}(\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}))(\operatorname{Frob}_{\ell })=\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D703}}(P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X))$
, so we deduce that
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }=\unicode[STIX]{x1D6EC}_{h}[\{\operatorname{Tr}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}(g))\}\text{}_{g\in G_{\mathbb{Q}}}]$
. As the traces of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }=\unicode[STIX]{x1D6EC}_{h}[\{\operatorname{Tr}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}(g))\}\text{}_{g\in G_{\mathbb{Q}}}]$
. As the traces of
![]() $\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}$
belong to
$\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}$
belong to
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
, another application of Carayol’s theorem [Reference CarayolCar94, Théorème 1] provides us with a representation
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
, another application of Carayol’s theorem [Reference CarayolCar94, Théorème 1] provides us with a representation
that is isomorphic to
![]() $\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}$
over
$\unicode[STIX]{x1D70C}_{\mathbb{I}^{\circ }}$
over
![]() $\mathbb{I}^{\circ }$
. Thanks to the following lemma we can attach to
$\mathbb{I}^{\circ }$
. Thanks to the following lemma we can attach to
![]() $\unicode[STIX]{x1D703}$
a symplectic representation.
$\unicode[STIX]{x1D703}$
a symplectic representation.
Lemma 4.7. There exists a non-degenerate symplectic bilinear form on
![]() $(\mathbb{I}_{\operatorname{Tr}}^{\circ })^{4}$
that is preserved up to a scalar by the image of
$(\mathbb{I}_{\operatorname{Tr}}^{\circ })^{4}$
that is preserved up to a scalar by the image of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
.
Proof. The argument of the proof is similar to that in [Reference Genestier and TilouineGT05, Lemma 4.3.3] and [Reference PilloniPil12, Proposition 6.4]. We show that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
is essentially self-dual by interpolating the characters that appear in the essential self-duality conditions at the classical specializations. We deduce that
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
is essentially self-dual by interpolating the characters that appear in the essential self-duality conditions at the classical specializations. We deduce that
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
preserves a bilinear form on
$\operatorname{Im}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
preserves a bilinear form on
![]() $(\mathbb{I}_{\operatorname{Tr}}^{\circ })^{4}$
up to a scalar. Such a form is non-degenerate by the irreducibility of
$(\mathbb{I}_{\operatorname{Tr}}^{\circ })^{4}$
up to a scalar. Such a form is non-degenerate by the irreducibility of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
and it is symplectic because its specialization at a classical point is symplectic.◻
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
and it is symplectic because its specialization at a classical point is symplectic.◻
Thanks to the lemma, up to replacing
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
by a conjugate representation, we can suppose that it takes values in
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
by a conjugate representation, we can suppose that it takes values in
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. We call
$\operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. We call
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
the Galois representation associated with the family
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
the Galois representation associated with the family
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. In the following, we work mainly with this representation, so we denote it simply by
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. In the following, we work mainly with this representation, so we denote it simply by
![]() $\unicode[STIX]{x1D70C}$
. We write
$\unicode[STIX]{x1D70C}$
. We write
![]() $\mathbb{F}$
for the residue field of
$\mathbb{F}$
for the residue field of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
and
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
and
![]() $\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{F})$
for the residual representation associated with
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{F})$
for the residual representation associated with
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
Remark 4.8. Let
![]() $\unicode[STIX]{x1D700}$
be the Nebentypus of the family
$\unicode[STIX]{x1D700}$
be the Nebentypus of the family
![]() $\unicode[STIX]{x1D703}$
. By interpolating the determinants of the classical specializations of
$\unicode[STIX]{x1D703}$
. By interpolating the determinants of the classical specializations of
![]() $\unicode[STIX]{x1D70C}$
, we obtain
$\unicode[STIX]{x1D70C}$
, we obtain
for every
![]() $g\in G_{\mathbb{Q}}$
.
$g\in G_{\mathbb{Q}}$
.
5 Conjugate self-twists of Galois representations attached to finite slope families
Given a ring
![]() $R$
, we denote by
$R$
, we denote by
![]() $Q(R)$
its total ring of fractions and by
$Q(R)$
its total ring of fractions and by
![]() $R^{\operatorname{norm}}$
its normalization. Now let
$R^{\operatorname{norm}}$
its normalization. Now let
![]() $R$
be an integral domain. For every homomorphism
$R$
be an integral domain. For every homomorphism
![]() $\unicode[STIX]{x1D70E}:R\rightarrow R$
and every
$\unicode[STIX]{x1D70E}:R\rightarrow R$
and every
![]() $\unicode[STIX]{x1D6FE}\in \operatorname{GSp}_{4}(R)$
, we define
$\unicode[STIX]{x1D6FE}\in \operatorname{GSp}_{4}(R)$
, we define
![]() $\unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D70E}}\in \operatorname{GSp}_{4}(R)$
by applying
$\unicode[STIX]{x1D6FE}^{\unicode[STIX]{x1D70E}}\in \operatorname{GSp}_{4}(R)$
by applying
![]() $\unicode[STIX]{x1D70E}$
to each coefficient of the matrix
$\unicode[STIX]{x1D70E}$
to each coefficient of the matrix
![]() $\unicode[STIX]{x1D6FE}$
. This way
$\unicode[STIX]{x1D6FE}$
. This way
![]() $\unicode[STIX]{x1D70E}$
induces a group automorphism
$\unicode[STIX]{x1D70E}$
induces a group automorphism
![]() $[\cdot ]^{\unicode[STIX]{x1D70E}}:G(R)\rightarrow G(R)$
for every algebraic subgroup
$[\cdot ]^{\unicode[STIX]{x1D70E}}:G(R)\rightarrow G(R)$
for every algebraic subgroup
![]() $G\subset \operatorname{GSp}_{4}$
defined over
$G\subset \operatorname{GSp}_{4}$
defined over
![]() $R$
. For such a
$R$
. For such a
![]() $G$
and any representation
$G$
and any representation
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow G(R)$
, we define a representation
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow G(R)$
, we define a representation
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow G(R)$
by setting
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow G(R)$
by setting
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}(g)=(\unicode[STIX]{x1D70C}(g))^{\unicode[STIX]{x1D70E}}$
for every
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}(g)=(\unicode[STIX]{x1D70C}(g))^{\unicode[STIX]{x1D70E}}$
for every
![]() $g\in G_{\mathbb{Q}}$
.
$g\in G_{\mathbb{Q}}$
.
Let
![]() $S$
be a subring of
$S$
be a subring of
![]() $R$
. We say that a homomorphism
$R$
. We say that a homomorphism
![]() $\unicode[STIX]{x1D70E}:R\rightarrow R$
is a homomorphism of
$\unicode[STIX]{x1D70E}:R\rightarrow R$
is a homomorphism of
![]() $R$
over
$R$
over
![]() $S$
if the restriction of
$S$
if the restriction of
![]() $\unicode[STIX]{x1D70E}$
to
$\unicode[STIX]{x1D70E}$
to
![]() $S$
is the identity. The following definition is inspired by [Reference RibetRib85, §3] and [Reference LangLan16, Definition 2.1].
$S$
is the identity. The following definition is inspired by [Reference RibetRib85, §3] and [Reference LangLan16, Definition 2.1].
Definition 5.1. Let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(R)$
be a representation. We call conjugate self-twist for
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(R)$
be a representation. We call conjugate self-twist for
![]() $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
![]() $S$
an automorphism
$S$
an automorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $R$
over
$R$
over
![]() $S$
such that there is a finite-order character
$S$
such that there is a finite-order character
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow R^{\times }$
and an isomorphism of representations over
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow R^{\times }$
and an isomorphism of representations over
![]() $R$
:
$R$
:
We list some basic facts about conjugate self-twists. The proofs are straightforward.
Proposition 5.2. Let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(R)$
be a representation.
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(R)$
be a representation.
(i) The conjugate self-twists for
 $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
 $S$
form a group.
$S$
form a group.(ii) Suppose that the identity of
 $R$
is not a conjugate self-twist for
$R$
is not a conjugate self-twist for
 $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
 $S$
. Then for every conjugate self-twist
$S$
. Then for every conjugate self-twist
 $\unicode[STIX]{x1D70E}$
the character
$\unicode[STIX]{x1D70E}$
the character
 $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
satisfying the equivalence (7) is uniquely determined.
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
satisfying the equivalence (7) is uniquely determined.(iii) Under the same hypotheses as part (ii), the association
 $\unicode[STIX]{x1D70E}\mapsto \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
defines a cocycle on the group of conjugate self-twists with values in
$\unicode[STIX]{x1D70E}\mapsto \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
defines a cocycle on the group of conjugate self-twists with values in
 $R^{\times }$
.
$R^{\times }$
.(iv) Let
 $S[\operatorname{Tr}\operatorname{Ad}\unicode[STIX]{x1D70C}]$
denote the ring generated over
$S[\operatorname{Tr}\operatorname{Ad}\unicode[STIX]{x1D70C}]$
denote the ring generated over
 $S$
by the set
$S$
by the set
 $\{\operatorname{Tr}(\operatorname{Ad}(\unicode[STIX]{x1D70C})(g))\}\text{}_{g\in G_{\mathbb{Q}}}$
. Then every element of
$\{\operatorname{Tr}(\operatorname{Ad}(\unicode[STIX]{x1D70C})(g))\}\text{}_{g\in G_{\mathbb{Q}}}$
. Then every element of
 $S[\operatorname{Tr}\operatorname{Ad}\unicode[STIX]{x1D70C}]$
is fixed by all conjugate self-twists for
$S[\operatorname{Tr}\operatorname{Ad}\unicode[STIX]{x1D70C}]$
is fixed by all conjugate self-twists for
 $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
 $S$
.
$S$
.
Let
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a family of
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a family of
![]() $\operatorname{GSp}_{4}$
-eigenforms as defined in §4. Let
$\operatorname{GSp}_{4}$
-eigenforms as defined in §4. Let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the Galois representation associated with
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the Galois representation associated with
![]() $\unicode[STIX]{x1D703}$
. Recall that
$\unicode[STIX]{x1D703}$
. Recall that
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is generated over
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is generated over
![]() $\unicode[STIX]{x1D6EC}_{h}$
by the traces of
$\unicode[STIX]{x1D6EC}_{h}$
by the traces of
![]() $\unicode[STIX]{x1D70C}$
. We always assume that
$\unicode[STIX]{x1D70C}$
. We always assume that
![]() $\overline{\unicode[STIX]{x1D70C}}$
is absolutely irreducible. Let
$\overline{\unicode[STIX]{x1D70C}}$
is absolutely irreducible. Let
![]() $\unicode[STIX]{x1D6E4}$
be the group of conjugate self-twists for
$\unicode[STIX]{x1D6E4}$
be the group of conjugate self-twists for
![]() $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
![]() $\unicode[STIX]{x1D6EC}_{h}$
. We omit the reference to
$\unicode[STIX]{x1D6EC}_{h}$
. We omit the reference to
![]() $\unicode[STIX]{x1D6EC}_{h}$
from now on and we just speak of the conjugate self-twists for
$\unicode[STIX]{x1D6EC}_{h}$
from now on and we just speak of the conjugate self-twists for
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
Remark 5.3. An argument completely analogous to that of [Reference LangLan16, Proposition 7.1] proves that the only possible prime factors of the order of
![]() $\unicode[STIX]{x1D6E4}$
are
$\unicode[STIX]{x1D6E4}$
are
![]() $2$
and
$2$
and
![]() $3$
.
$3$
.
We denote by
![]() $\mathbb{I}_{0}^{\circ }$
the subring
$\mathbb{I}_{0}^{\circ }$
the subring
![]() $(\mathbb{I}_{\operatorname{Tr}}^{\circ })^{\unicode[STIX]{x1D6E4}}$
of
$(\mathbb{I}_{\operatorname{Tr}}^{\circ })^{\unicode[STIX]{x1D6E4}}$
of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
consisting of the elements fixed by every
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
consisting of the elements fixed by every
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
.
5.1 Lifting conjugate self-twists from classical points to families
Keep the notation as above. Let
![]() $P_{\text{}\underline{k}}\subset \unicode[STIX]{x1D6EC}_{h}$
be any non-critical arithmetic prime, as in Definition 4.5. The representation
$P_{\text{}\underline{k}}\subset \unicode[STIX]{x1D6EC}_{h}$
be any non-critical arithmetic prime, as in Definition 4.5. The representation
![]() $\unicode[STIX]{x1D70C}$
can be reduced modulo
$\unicode[STIX]{x1D70C}$
can be reduced modulo
![]() $P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
to a representation
$P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
to a representation
![]() $\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. Let
$\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. Let
![]() $\widetilde{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6E4}$
and let
$\widetilde{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6E4}$
and let
![]() $\widetilde{\unicode[STIX]{x1D702}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ })^{\times }$
be the character associated with
$\widetilde{\unicode[STIX]{x1D702}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ })^{\times }$
be the character associated with
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
. The automorphism
$\widetilde{\unicode[STIX]{x1D70E}}$
. The automorphism
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
induces a ring automorphism
$\widetilde{\unicode[STIX]{x1D70E}}$
induces a ring automorphism
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{P_{\text{}\underline{k}}}$
of
$\widetilde{\unicode[STIX]{x1D70E}}_{P_{\text{}\underline{k}}}$
of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
. The character
$\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
. The character
![]() $\widetilde{\unicode[STIX]{x1D702}}:G_{\mathbb{Q}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
induces a character
$\widetilde{\unicode[STIX]{x1D702}}:G_{\mathbb{Q}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
induces a character
![]() $\widetilde{\unicode[STIX]{x1D702}}_{P_{\text{}\underline{k}}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ })^{\times }$
, satisfying
$\widetilde{\unicode[STIX]{x1D702}}_{P_{\text{}\underline{k}}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ })^{\times }$
, satisfying
As
![]() $P_{\text{}\underline{k}}$
is non-critical,
$P_{\text{}\underline{k}}$
is non-critical,
![]() $\mathbb{I}^{\circ }$
is étale over
$\mathbb{I}^{\circ }$
is étale over
![]() $\unicode[STIX]{x1D6EC}_{h}$
at
$\unicode[STIX]{x1D6EC}_{h}$
at
![]() $P_{\text{}\underline{k}}$
, so
$P_{\text{}\underline{k}}$
, so
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is also étale over
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
is also étale over
![]() $\unicode[STIX]{x1D6EC}_{h}$
at
$\unicode[STIX]{x1D6EC}_{h}$
at
![]() $P_{\text{}\underline{k}}$
. In particular,
$P_{\text{}\underline{k}}$
. In particular,
![]() $P_{\text{}\underline{k}}$
is a product of distinct primes in
$P_{\text{}\underline{k}}$
is a product of distinct primes in
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
; denote them by
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
; denote them by
![]() $\mathfrak{P}_{1},\mathfrak{P}_{2},\ldots ,\mathfrak{P}_{d}$
. As
$\mathfrak{P}_{1},\mathfrak{P}_{2},\ldots ,\mathfrak{P}_{d}$
. As
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{P_{\text{}\underline{k}}}$
is an automorphism of
$\widetilde{\unicode[STIX]{x1D70E}}_{P_{\text{}\underline{k}}}$
is an automorphism of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ }\cong \prod _{i=1}^{d}\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}$
, there is a permutation
$\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{\operatorname{Tr}}^{\circ }\cong \prod _{i=1}^{d}\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}$
, there is a permutation
![]() $s$
of the set
$s$
of the set
![]() $\{1,2,\ldots ,d\}$
and isomorphisms
$\{1,2,\ldots ,d\}$
and isomorphisms
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}:\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{s(i)}$
for
$\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}:\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{s(i)}$
for
![]() $i=1,2,\ldots ,d$
such that
$i=1,2,\ldots ,d$
such that
![]() $\widetilde{\unicode[STIX]{x1D70E}}|_{\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}}$
factors through
$\widetilde{\unicode[STIX]{x1D70E}}|_{\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}}$
factors through
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}$
. The character
$\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}$
. The character
![]() $\widetilde{\unicode[STIX]{x1D702}}_{\widetilde{\unicode[STIX]{x1D70E}}_{P_{\text{}\underline{k}}}}$
can be written as a product
$\widetilde{\unicode[STIX]{x1D702}}_{\widetilde{\unicode[STIX]{x1D70E}}_{P_{\text{}\underline{k}}}}$
can be written as a product
![]() $\prod _{i=1}^{d}\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{i}}$
for some characters
$\prod _{i=1}^{d}\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{i}}$
for some characters
![]() $\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{i}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i})^{\times }$
. From the equivalence (8), we deduce that
$\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{i}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i})^{\times }$
. From the equivalence (8), we deduce that
The goal of this subsection is to prove that if we are given, for a single value of
![]() $i$
, data
$i$
, data
![]() $s(i)$
,
$s(i)$
,
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}$
and
![]() $\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{i}}$
satisfying the isomorphism above, then there exists an element of
$\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{i}}$
satisfying the isomorphism above, then there exists an element of
![]() $\unicode[STIX]{x1D6E4}$
giving rise to
$\unicode[STIX]{x1D6E4}$
giving rise to
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}$
and
![]() $\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{s_{i}}}$
via reduction modulo
$\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{s_{i}}}$
via reduction modulo
![]() $P_{\text{}\underline{k}}$
. This result is an analogue of [Reference LangLan16, Theorem 3.1]. We state it precisely in the following proposition.
$P_{\text{}\underline{k}}$
. This result is an analogue of [Reference LangLan16, Theorem 3.1]. We state it precisely in the following proposition.
Proposition 5.4. Let
![]() $i,j\in \{1,2,\ldots ,d\}$
. Let
$i,j\in \{1,2,\ldots ,d\}$
. Let
![]() $\unicode[STIX]{x1D70E}:\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j}$
be a ring isomorphism and let
$\unicode[STIX]{x1D70E}:\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j}$
be a ring isomorphism and let
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j})^{\times }$
be a character satisfying
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j})^{\times }$
be a character satisfying
Then there exists
![]() $\widetilde{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6E4}$
with associated character
$\widetilde{\unicode[STIX]{x1D70E}}\in \unicode[STIX]{x1D6E4}$
with associated character
![]() $\widetilde{\unicode[STIX]{x1D702}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ })^{\times }$
such that, via the construction of the previous paragraph,
$\widetilde{\unicode[STIX]{x1D702}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ })^{\times }$
such that, via the construction of the previous paragraph,
![]() $s(i)=j$
,
$s(i)=j$
,
![]() $\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}=\unicode[STIX]{x1D70E}$
and
$\widetilde{\unicode[STIX]{x1D70E}}_{\mathfrak{P}_{i}}=\unicode[STIX]{x1D70E}$
and
![]() $\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{j}}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
.
$\widetilde{\unicode[STIX]{x1D702}}_{\mathfrak{P}_{j}}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
.
To prove the proposition, we first lift
![]() $\unicode[STIX]{x1D70E}$
to an automorphism
$\unicode[STIX]{x1D70E}$
to an automorphism
![]() $\unicode[STIX]{x1D6F4}$
of a deformation ring for
$\unicode[STIX]{x1D6F4}$
of a deformation ring for
![]() $\overline{\unicode[STIX]{x1D70C}}$
and then we show that
$\overline{\unicode[STIX]{x1D70C}}$
and then we show that
![]() $\unicode[STIX]{x1D6F4}$
descends to a conjugate self-twist for
$\unicode[STIX]{x1D6F4}$
descends to a conjugate self-twist for
![]() $\unicode[STIX]{x1D70C}$
. This strategy is the same as that of the proof of [Reference LangLan16, Theorem 3.1], but there are various complications that have to be taken care of. We refer to [Reference ContiCon16, §4.4] for the technical lemmas that generalize Lang’s result, and we report here only the core elements of the proof.
$\unicode[STIX]{x1D70C}$
. This strategy is the same as that of the proof of [Reference LangLan16, Theorem 3.1], but there are various complications that have to be taken care of. We refer to [Reference ContiCon16, §4.4] for the technical lemmas that generalize Lang’s result, and we report here only the core elements of the proof.
Before proving Proposition 5.4 we give a corollary. Let
![]() $\mathfrak{P}\in \{\mathfrak{P}_{1},\mathfrak{P}_{2},\ldots ,\mathfrak{P}_{d}\}$
. Let
$\mathfrak{P}\in \{\mathfrak{P}_{1},\mathfrak{P}_{2},\ldots ,\mathfrak{P}_{d}\}$
. Let
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{P}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P})$
be the reduction of
$\unicode[STIX]{x1D70C}_{\mathfrak{P}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P})$
be the reduction of
![]() $\unicode[STIX]{x1D70C}$
modulo
$\unicode[STIX]{x1D70C}$
modulo
![]() $\mathfrak{P}$
and let
$\mathfrak{P}$
and let
![]() $\unicode[STIX]{x1D6E4}_{\mathfrak{P}}$
be the group of conjugate self-twists for
$\unicode[STIX]{x1D6E4}_{\mathfrak{P}}$
be the group of conjugate self-twists for
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{P}}$
over
$\unicode[STIX]{x1D70C}_{\mathfrak{P}}$
over
![]() $\mathbb{Z}_{p}$
. Let
$\mathbb{Z}_{p}$
. Let
![]() $\unicode[STIX]{x1D6E4}(\mathfrak{P})=\{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}\,|\,\unicode[STIX]{x1D70E}(\mathfrak{P})=\mathfrak{P}\}$
. The reduction of the elements of
$\unicode[STIX]{x1D6E4}(\mathfrak{P})=\{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}\,|\,\unicode[STIX]{x1D70E}(\mathfrak{P})=\mathfrak{P}\}$
. The reduction of the elements of
![]() $\unicode[STIX]{x1D6E4}(\mathfrak{P})$
modulo
$\unicode[STIX]{x1D6E4}(\mathfrak{P})$
modulo
![]() $\mathfrak{P}$
defines a morphism of groups
$\mathfrak{P}$
defines a morphism of groups
![]() $\unicode[STIX]{x1D6E4}(\mathfrak{P})\rightarrow \unicode[STIX]{x1D6E4}_{\mathfrak{P}}$
. Choosing
$\unicode[STIX]{x1D6E4}(\mathfrak{P})\rightarrow \unicode[STIX]{x1D6E4}_{\mathfrak{P}}$
. Choosing
![]() $\mathfrak{P}_{i}=\mathfrak{P}_{j}=\mathfrak{P}$
in Proposition 5.4 gives the following result.
$\mathfrak{P}_{i}=\mathfrak{P}_{j}=\mathfrak{P}$
in Proposition 5.4 gives the following result.
Corollary 5.5. The morphism
![]() $\unicode[STIX]{x1D6E4}(\mathfrak{P})\rightarrow \unicode[STIX]{x1D6E4}_{\mathfrak{P}}$
is surjective.
$\unicode[STIX]{x1D6E4}(\mathfrak{P})\rightarrow \unicode[STIX]{x1D6E4}_{\mathfrak{P}}$
is surjective.
5.1.1 Lifting conjugate self-twists to the deformation ring
We keep the notation of the beginning of this section. We write
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
for simplicity. Let
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
for simplicity. Let
![]() $\mathbb{Q}^{Np}$
denote the maximal extension of
$\mathbb{Q}^{Np}$
denote the maximal extension of
![]() $\mathbb{Q}$
unramified outside
$\mathbb{Q}$
unramified outside
![]() $Np$
and set
$Np$
and set
![]() $G_{\mathbb{Q}}^{Np}=\operatorname{Gal}(\mathbb{Q}^{Np}/\mathbb{Q})$
. Then we can and do consider
$G_{\mathbb{Q}}^{Np}=\operatorname{Gal}(\mathbb{Q}^{Np}/\mathbb{Q})$
. Then we can and do consider
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D702}$
as representations of
$\unicode[STIX]{x1D702}$
as representations of
![]() $G_{\mathbb{Q}}^{Np}$
by Proposition 2.5 and (9).
$G_{\mathbb{Q}}^{Np}$
by Proposition 2.5 and (9).
Recall that we denote by
![]() $\mathfrak{m}_{\mathbb{I}_{\operatorname{Tr}}^{\circ }}$
the maximal ideal of
$\mathfrak{m}_{\mathbb{I}_{\operatorname{Tr}}^{\circ }}$
the maximal ideal of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
and by
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
and by
![]() $\mathbb{F}$
the residue field
$\mathbb{F}$
the residue field
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{m}_{\operatorname{Tr}^{\circ }}$
. Let
$\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{m}_{\operatorname{Tr}^{\circ }}$
. Let
![]() $W$
be the ring of Witt vectors of
$W$
be the ring of Witt vectors of
![]() $\mathbb{F}$
. The residual representation
$\mathbb{F}$
. The residual representation
![]() $\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}^{Np}\rightarrow \operatorname{GL}_{4}(\mathbb{F})$
is absolutely irreducible by assumption. By the results of [Reference MazurMaz89], the problem of deforming
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}^{Np}\rightarrow \operatorname{GL}_{4}(\mathbb{F})$
is absolutely irreducible by assumption. By the results of [Reference MazurMaz89], the problem of deforming
![]() $\unicode[STIX]{x1D70C}$
to a representation with coefficients in a Noetherian
$\unicode[STIX]{x1D70C}$
to a representation with coefficients in a Noetherian
![]() $W$
-algebra is represented by a universal couple
$W$
-algebra is represented by a universal couple
![]() $(R_{\overline{\unicode[STIX]{x1D70C}}},\unicode[STIX]{x1D70C}^{\operatorname{univ}})$
consisting of a Noetherian
$(R_{\overline{\unicode[STIX]{x1D70C}}},\unicode[STIX]{x1D70C}^{\operatorname{univ}})$
consisting of a Noetherian
![]() $W$
-algebra
$W$
-algebra
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}$
and a representation
$R_{\overline{\unicode[STIX]{x1D70C}}}$
and a representation
![]() $\unicode[STIX]{x1D70C}^{\operatorname{univ}}:G_{\mathbb{Q}}^{Np}\rightarrow \operatorname{GL}_{4}(R_{\overline{\unicode[STIX]{x1D70C}}})$
.
$\unicode[STIX]{x1D70C}^{\operatorname{univ}}:G_{\mathbb{Q}}^{Np}\rightarrow \operatorname{GL}_{4}(R_{\overline{\unicode[STIX]{x1D70C}}})$
.
By the universal property of
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}$
, there exists a unique morphism of
$R_{\overline{\unicode[STIX]{x1D70C}}}$
, there exists a unique morphism of
![]() $W$
-algebras
$W$
-algebras
![]() $\unicode[STIX]{x1D6FC}_{I}:R_{\overline{\unicode[STIX]{x1D70C}}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
satisfying
$\unicode[STIX]{x1D6FC}_{I}:R_{\overline{\unicode[STIX]{x1D70C}}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
satisfying
![]() $\unicode[STIX]{x1D70C}\cong \unicode[STIX]{x1D6FC}_{I}\circ \,\overline{\unicode[STIX]{x1D70C}}^{\operatorname{univ}}$
. Let
$\unicode[STIX]{x1D70C}\cong \unicode[STIX]{x1D6FC}_{I}\circ \,\overline{\unicode[STIX]{x1D70C}}^{\operatorname{univ}}$
. Let
![]() $\operatorname{ev}_{i}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}$
and
$\operatorname{ev}_{i}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}$
and
![]() $\operatorname{ev}_{j}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j}$
be the two projections. The following proposition follows from arguments completely analogous to those of [Reference LangLan16, §3.1]. The details of the proof can be found in [Reference ContiCon16, §4.4.1].
$\operatorname{ev}_{j}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j}$
be the two projections. The following proposition follows from arguments completely analogous to those of [Reference LangLan16, §3.1]. The details of the proof can be found in [Reference ContiCon16, §4.4.1].
Proposition 5.6.
(i) The automorphism
 $\overline{\unicode[STIX]{x1D70E}}$
of
$\overline{\unicode[STIX]{x1D70E}}$
of
 $\mathbb{F}$
is trivial.
$\mathbb{F}$
is trivial.(ii) There is an isomorphism
 $\overline{\unicode[STIX]{x1D70C}}\cong \overline{\unicode[STIX]{x1D702}}\otimes \overline{\unicode[STIX]{x1D70C}}$
.
$\overline{\unicode[STIX]{x1D70C}}\cong \overline{\unicode[STIX]{x1D702}}\otimes \overline{\unicode[STIX]{x1D70C}}$
.(iii) There exists an automorphism
 $\unicode[STIX]{x1D6F4}$
of
$\unicode[STIX]{x1D6F4}$
of
 $R_{\overline{\unicode[STIX]{x1D70C}}}$
such that:
$R_{\overline{\unicode[STIX]{x1D70C}}}$
such that:(a)
 $\unicode[STIX]{x1D6F4}$
is a lift of
$\unicode[STIX]{x1D6F4}$
is a lift of
 $\unicode[STIX]{x1D70E}$
in the sense that
$\unicode[STIX]{x1D70E}$
in the sense that
 $\unicode[STIX]{x1D70E}\circ \,\operatorname{ev}_{i}\circ \,\,\unicode[STIX]{x1D6FC}_{I}=\operatorname{ev}_{j}\circ \,\,\unicode[STIX]{x1D6FC}_{I}\circ \,\unicode[STIX]{x1D6F4}$
;
$\unicode[STIX]{x1D70E}\circ \,\operatorname{ev}_{i}\circ \,\,\unicode[STIX]{x1D6FC}_{I}=\operatorname{ev}_{j}\circ \,\,\unicode[STIX]{x1D6FC}_{I}\circ \,\unicode[STIX]{x1D6F4}$
;(b)
 $\unicode[STIX]{x1D6F4}\circ \,\unicode[STIX]{x1D70C}^{\operatorname{univ}}=\unicode[STIX]{x1D702}\circ \,\unicode[STIX]{x1D70C}^{\operatorname{univ}}$
.
$\unicode[STIX]{x1D6F4}\circ \,\unicode[STIX]{x1D70C}^{\operatorname{univ}}=\unicode[STIX]{x1D702}\circ \,\unicode[STIX]{x1D70C}^{\operatorname{univ}}$
.
We set
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D6FC}_{I}\circ \,\unicode[STIX]{x1D6F4}\circ \,\unicode[STIX]{x1D70C}^{\operatorname{univ}}$
. Recall that
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D6FC}_{I}\circ \,\unicode[STIX]{x1D6F4}\circ \,\unicode[STIX]{x1D70C}^{\operatorname{univ}}$
. Recall that
![]() $\unicode[STIX]{x1D70C}$
is the Galois representation associated with the finite slope family
$\unicode[STIX]{x1D70C}$
is the Galois representation associated with the finite slope family
![]() $\unicode[STIX]{x1D703}$
. Our next step consists of showing that
$\unicode[STIX]{x1D703}$
. Our next step consists of showing that
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6F4}}$
is associated with a family of
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6F4}}$
is associated with a family of
![]() $\operatorname{GSp}_{4}$
-eigenforms of a suitable tame level and slope bounded by
$\operatorname{GSp}_{4}$
-eigenforms of a suitable tame level and slope bounded by
![]() $h$
. Note that equality (b) in Proposition 5.6(iii) implies
$h$
. Note that equality (b) in Proposition 5.6(iii) implies
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6F4}}\cong \unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D70C}$
, so it is sufficient to show that the representation
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6F4}}\cong \unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D70C}$
, so it is sufficient to show that the representation
![]() $\unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D70C}$
is associated with a family with the prescribed properties.
$\unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D70C}$
is associated with a family with the prescribed properties.
5.1.2 Twisting families by finite-order characters
We show that the twist of the Galois representation associated with a family of
![]() $\operatorname{GSp}_{4}$
-eigenforms is again associated with such a family. We deduce this by the analogous result for a single classical Siegel eigenform, proved in [Reference ContiCon16, §4.5].
$\operatorname{GSp}_{4}$
-eigenforms is again associated with such a family. We deduce this by the analogous result for a single classical Siegel eigenform, proved in [Reference ContiCon16, §4.5].
Let
![]() $f$
be a cuspidal
$f$
be a cuspidal
![]() $\operatorname{GSp}_{4}$
-eigenform of weight
$\operatorname{GSp}_{4}$
-eigenform of weight
![]() $(k_{1},k_{2})$
and level
$(k_{1},k_{2})$
and level
![]() $\unicode[STIX]{x1D6E4}_{1}(M)$
and let
$\unicode[STIX]{x1D6E4}_{1}(M)$
and let
![]() $\unicode[STIX]{x1D70C}_{f,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\overline{\mathbb{Q}}_{p})$
be the
$\unicode[STIX]{x1D70C}_{f,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\overline{\mathbb{Q}}_{p})$
be the
![]() $p$
-adic Galois representation attached to
$p$
-adic Galois representation attached to
![]() $f$
. Let
$f$
. Let
![]() $\unicode[STIX]{x1D702}:G_{\mathbb{Q}}\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
be a character of finite order
$\unicode[STIX]{x1D702}:G_{\mathbb{Q}}\rightarrow \overline{\mathbb{Q}}_{p}^{\times }$
be a character of finite order
![]() $m_{0}$
prime to
$m_{0}$
prime to
![]() $p$
. We see
$p$
. We see
![]() $\unicode[STIX]{x1D702}$
as a Dirichlet character when convenient.
$\unicode[STIX]{x1D702}$
as a Dirichlet character when convenient.
Proposition 5.7 [Reference ContiCon16, Corollary 4.5.5].
Let
![]() $M^{\prime }=\operatorname{lcm}(m_{0},M)^{2}$
. Let
$M^{\prime }=\operatorname{lcm}(m_{0},M)^{2}$
. Let
![]() $x$
be a classical
$x$
be a classical
![]() $p$
-old point of
$p$
-old point of
![]() ${\mathcal{D}}_{2}^{M}$
having weight
${\mathcal{D}}_{2}^{M}$
having weight
![]() $(k_{1},k_{2})$
, slope
$(k_{1},k_{2})$
, slope
![]() $h$
and associated Galois representation
$h$
and associated Galois representation
![]() $\unicode[STIX]{x1D70C}_{x}$
. Then there exists a classical
$\unicode[STIX]{x1D70C}_{x}$
. Then there exists a classical
![]() $p$
-old point
$p$
-old point
![]() $x_{\unicode[STIX]{x1D702}}$
of
$x_{\unicode[STIX]{x1D702}}$
of
![]() ${\mathcal{D}}_{2}^{M^{\prime }}$
having weight
${\mathcal{D}}_{2}^{M^{\prime }}$
having weight
![]() $(k_{1},k_{2})$
, slope
$(k_{1},k_{2})$
, slope
![]() $h$
and associated Galois representation
$h$
and associated Galois representation
![]() $\unicode[STIX]{x1D70C}_{x_{\unicode[STIX]{x1D702}}}=\unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D70C}_{x}$
.
$\unicode[STIX]{x1D70C}_{x_{\unicode[STIX]{x1D702}}}=\unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D70C}_{x}$
.
We remark that the proof relies on the calculations made by Andrianov in [Reference AndrianovAnd09, §1]. He only considers the case
![]() $k_{1}=k_{2}$
, but his work is easily adapted to vector-valued forms.
$k_{1}=k_{2}$
, but his work is easily adapted to vector-valued forms.
Now consider the family
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
fixed in the beginning of the section. For every
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
fixed in the beginning of the section. For every
![]() $p$
-old classical point
$p$
-old classical point
![]() $x$
of
$x$
of
![]() $\unicode[STIX]{x1D703}$
, let
$\unicode[STIX]{x1D703}$
, let
![]() $x_{\unicode[STIX]{x1D702}}$
be the point of the eigenvariety
$x_{\unicode[STIX]{x1D702}}$
be the point of the eigenvariety
![]() ${\mathcal{D}}_{2}^{M^{\prime }}$
provided by Proposition 5.7. Let
${\mathcal{D}}_{2}^{M^{\prime }}$
provided by Proposition 5.7. Let
![]() $r_{h}^{\prime }$
be a radius adapted to
$r_{h}^{\prime }$
be a radius adapted to
![]() $h$
for the eigenvariety
$h$
for the eigenvariety
![]() ${\mathcal{D}}_{2}^{M^{\prime }}$
. Let
${\mathcal{D}}_{2}^{M^{\prime }}$
. Let
![]() $\unicode[STIX]{x1D6EC}_{h}^{\prime }$
be the genus
$\unicode[STIX]{x1D6EC}_{h}^{\prime }$
be the genus
![]() $2$
,
$2$
,
![]() $h$
-adapted Iwasawa algebra for
$h$
-adapted Iwasawa algebra for
![]() ${\mathcal{D}}_{2}^{M^{\prime }}$
and let
${\mathcal{D}}_{2}^{M^{\prime }}$
and let
![]() $\mathbb{T}_{h}^{\prime }$
be the genus
$\mathbb{T}_{h}^{\prime }$
be the genus
![]() $2$
,
$2$
,
![]() $h$
-adapted Hecke algebra of level
$h$
-adapted Hecke algebra of level
![]() $M^{\prime }$
. Note that
$M^{\prime }$
. Note that
![]() $r_{h}^{\prime }\leqslant r_{h}$
, so there is a natural map
$r_{h}^{\prime }\leqslant r_{h}$
, so there is a natural map
![]() $\unicode[STIX]{x1D704}_{h}:\unicode[STIX]{x1D6EC}_{h}\rightarrow \unicode[STIX]{x1D6EC}_{h}^{\prime }$
. All tensor products with
$\unicode[STIX]{x1D704}_{h}:\unicode[STIX]{x1D6EC}_{h}\rightarrow \unicode[STIX]{x1D6EC}_{h}^{\prime }$
. All tensor products with
![]() $\unicode[STIX]{x1D6EC}_{h}^{\prime }$
over
$\unicode[STIX]{x1D6EC}_{h}^{\prime }$
over
![]() $\unicode[STIX]{x1D6EC}_{h}$
will be taken with respect to
$\unicode[STIX]{x1D6EC}_{h}$
will be taken with respect to
![]() $\unicode[STIX]{x1D704}_{h}$
. We can see
$\unicode[STIX]{x1D704}_{h}$
. We can see
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
as an
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
as an
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
-valued representation via
$\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
-valued representation via
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime },a\mapsto a\otimes 1$
. We do this implicitly in the following.
$\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime },a\mapsto a\otimes 1$
. We do this implicitly in the following.
Lemma 5.8. There exists a finite
![]() $\unicode[STIX]{x1D6EC}_{h}^{\prime }$
-algebra
$\unicode[STIX]{x1D6EC}_{h}^{\prime }$
-algebra
![]() $\mathbb{J}^{\circ }$
, a family
$\mathbb{J}^{\circ }$
, a family
![]() $\unicode[STIX]{x1D703}^{\prime }:\mathbb{T}_{h}^{\prime }\rightarrow \mathbb{J}^{\circ }$
and an isomorphism
$\unicode[STIX]{x1D703}^{\prime }:\mathbb{T}_{h}^{\prime }\rightarrow \mathbb{J}^{\circ }$
and an isomorphism
![]() $\unicode[STIX]{x1D6FC}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }\rightarrow \mathbb{J}_{\operatorname{Tr}}^{\circ }$
such that the representation
$\unicode[STIX]{x1D6FC}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }\rightarrow \mathbb{J}_{\operatorname{Tr}}^{\circ }$
such that the representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{J}_{\operatorname{Tr}}^{\circ })$
associated with
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{J}_{\operatorname{Tr}}^{\circ })$
associated with
![]() $\unicode[STIX]{x1D703}^{\prime }$
satisfies
$\unicode[STIX]{x1D703}^{\prime }$
satisfies
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}\cong \unicode[STIX]{x1D702}\otimes (\unicode[STIX]{x1D6FC}\circ \,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}})$
.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}\cong \unicode[STIX]{x1D702}\otimes (\unicode[STIX]{x1D6FC}\circ \,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}})$
.
Remark 5.9. With the notation of the proof of Lemma 5.8, all points of the set
![]() $S_{\unicode[STIX]{x1D702}}^{\prime }$
belong to the family
$S_{\unicode[STIX]{x1D702}}^{\prime }$
belong to the family
![]() $\unicode[STIX]{x1D703}^{\prime }$
, because of the unicity of a point of
$\unicode[STIX]{x1D703}^{\prime }$
, because of the unicity of a point of
![]() ${\mathcal{D}}_{2}^{M^{\prime }}$
given its associated Galois representation and slope.
${\mathcal{D}}_{2}^{M^{\prime }}$
given its associated Galois representation and slope.
By combining Lemma 5.8 and Proposition 5.6(iii) we obtain the following.
Corollary 5.10. There exists a finite
![]() $\unicode[STIX]{x1D6EC}_{h}^{\prime }$
-algebra
$\unicode[STIX]{x1D6EC}_{h}^{\prime }$
-algebra
![]() $\mathbb{J}^{\circ }$
, a family
$\mathbb{J}^{\circ }$
, a family
![]() $\unicode[STIX]{x1D703}^{\prime }:\mathbb{T}_{h}^{\prime }\rightarrow \mathbb{J}^{\circ }$
and an isomorphism
$\unicode[STIX]{x1D703}^{\prime }:\mathbb{T}_{h}^{\prime }\rightarrow \mathbb{J}^{\circ }$
and an isomorphism
![]() $\unicode[STIX]{x1D6FC}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }\rightarrow \mathbb{J}_{\operatorname{Tr}}^{\circ }$
such that the representation
$\unicode[STIX]{x1D6FC}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }\rightarrow \mathbb{J}_{\operatorname{Tr}}^{\circ }$
such that the representation
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{J}_{\operatorname{Tr}}^{\circ })$
associated with
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{J}_{\operatorname{Tr}}^{\circ })$
associated with
![]() $\unicode[STIX]{x1D703}^{\prime }$
satisfies
$\unicode[STIX]{x1D703}^{\prime }$
satisfies
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}\cong \unicode[STIX]{x1D6FC}\circ \,\unicode[STIX]{x1D6F4}\circ \,\unicode[STIX]{x1D70C}^{\operatorname{univ}}$
.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}\cong \unicode[STIX]{x1D6FC}\circ \,\unicode[STIX]{x1D6F4}\circ \,\unicode[STIX]{x1D70C}^{\operatorname{univ}}$
.
5.1.3 Descending to a conjugate self-twist of the family
We show that the automorphism
![]() $\unicode[STIX]{x1D6F4}$
of
$\unicode[STIX]{x1D6F4}$
of
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}$
defined in the previous subsection induces a conjugate self-twist for
$R_{\overline{\unicode[STIX]{x1D70C}}}$
defined in the previous subsection induces a conjugate self-twist for
![]() $\unicode[STIX]{x1D70C}$
. This will prove Proposition 5.4. Our argument is an analogue for
$\unicode[STIX]{x1D70C}$
. This will prove Proposition 5.4. Our argument is an analogue for
![]() $\operatorname{GSp}_{4}$
of that in the end of the proof of [Reference LangLan16, Theorem 3.1]; it also appears in similar forms in [Reference FischmanFis02, Proposition 3.12] and [Reference Dimitrov and GhateDG12, Proposition A.3]. Here the non-criticality of the prime
$\operatorname{GSp}_{4}$
of that in the end of the proof of [Reference LangLan16, Theorem 3.1]; it also appears in similar forms in [Reference FischmanFis02, Proposition 3.12] and [Reference Dimitrov and GhateDG12, Proposition A.3]. Here the non-criticality of the prime
![]() $P_{\text{}\underline{k}}$
plays an important role.
$P_{\text{}\underline{k}}$
plays an important role.
Proof of Proposition 5.4.
Let
![]() $\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{F})$
be the residual representation associated with
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{F})$
be the residual representation associated with
![]() $\unicode[STIX]{x1D70C}$
. Let
$\unicode[STIX]{x1D70C}$
. Let
![]() $R_{\overline{\unicode[STIX]{x1D70C}}}$
be the universal deformation ring associated with
$R_{\overline{\unicode[STIX]{x1D70C}}}$
be the universal deformation ring associated with
![]() $\overline{\unicode[STIX]{x1D70C}}$
and let
$\overline{\unicode[STIX]{x1D70C}}$
and let
![]() $\overline{\unicode[STIX]{x1D70C}}^{\operatorname{univ}}$
be the corresponding universal deformation. As before let
$\overline{\unicode[STIX]{x1D70C}}^{\operatorname{univ}}$
be the corresponding universal deformation. As before let
![]() $\unicode[STIX]{x1D6FC}_{I}:R_{\overline{\unicode[STIX]{x1D70C}}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
be the unique morphism of
$\unicode[STIX]{x1D6FC}_{I}:R_{\overline{\unicode[STIX]{x1D70C}}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
be the unique morphism of
![]() $W$
-algebras
$W$
-algebras
![]() $\unicode[STIX]{x1D6FC}_{I}:R_{\overline{\unicode[STIX]{x1D70C}}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
satisfying
$\unicode[STIX]{x1D6FC}_{I}:R_{\overline{\unicode[STIX]{x1D70C}}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
satisfying
![]() $\unicode[STIX]{x1D70C}\cong \unicode[STIX]{x1D6FC}_{I}\circ \,\overline{\unicode[STIX]{x1D70C}}^{\operatorname{univ}}$
.
$\unicode[STIX]{x1D70C}\cong \unicode[STIX]{x1D6FC}_{I}\circ \,\overline{\unicode[STIX]{x1D70C}}^{\operatorname{univ}}$
.
Consider the morphism of
![]() $W$
-algebras
$W$
-algebras
![]() $\unicode[STIX]{x1D6FC}_{I}^{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D6FC}_{I}\circ \,\unicode[STIX]{x1D6F4}:R_{\overline{\unicode[STIX]{x1D70C}}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. We show that there exists an automorphism
$\unicode[STIX]{x1D6FC}_{I}^{\unicode[STIX]{x1D6F4}}=\unicode[STIX]{x1D6FC}_{I}\circ \,\unicode[STIX]{x1D6F4}:R_{\overline{\unicode[STIX]{x1D70C}}}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. We show that there exists an automorphism
![]() $\widetilde{\unicode[STIX]{x1D70E}}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
fitting in the following commutative diagram.
$\widetilde{\unicode[STIX]{x1D70E}}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
fitting in the following commutative diagram.

We use the notation of the discussion preceding Lemma 5.8. Consider the morphism
![]() $\unicode[STIX]{x1D703}\otimes 1:\mathbb{T}_{h}\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }\rightarrow \mathbb{I}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
. For every
$\unicode[STIX]{x1D703}\otimes 1:\mathbb{T}_{h}\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }\rightarrow \mathbb{I}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
. For every
![]() $\unicode[STIX]{x1D6EC}_{h}$
-algebra
$\unicode[STIX]{x1D6EC}_{h}$
-algebra
![]() $A$
we denote again by
$A$
we denote again by
![]() $\unicode[STIX]{x1D704}_{h}$
the map
$\unicode[STIX]{x1D704}_{h}$
the map
![]() $A\rightarrow A\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime },a\mapsto a\otimes 1$
. The natural inclusion
$A\rightarrow A\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime },a\mapsto a\otimes 1$
. The natural inclusion
![]() ${\mathcal{D}}_{2}^{M}{\hookrightarrow}{\mathcal{D}}_{2}^{M^{\prime }}$
induces a surjection
${\mathcal{D}}_{2}^{M}{\hookrightarrow}{\mathcal{D}}_{2}^{M^{\prime }}$
induces a surjection
![]() $s_{h}:\mathbb{T}_{h}^{\prime }\rightarrow \mathbb{T}_{h}\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
. We define a family of tame level
$s_{h}:\mathbb{T}_{h}^{\prime }\rightarrow \mathbb{T}_{h}\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
. We define a family of tame level
![]() $\unicode[STIX]{x1D6E4}_{1}(M^{\prime })$
and slope bounded by
$\unicode[STIX]{x1D6E4}_{1}(M^{\prime })$
and slope bounded by
![]() $h$
by
$h$
by
The Galois representation associated with
![]() $\unicode[STIX]{x1D703}^{M^{\prime }}$
is
$\unicode[STIX]{x1D703}^{M^{\prime }}$
is
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{M^{\prime }}}=\unicode[STIX]{x1D704}_{h}\circ \,\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime })$
. Let
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{M^{\prime }}}=\unicode[STIX]{x1D704}_{h}\circ \,\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime })$
. Let
![]() $\unicode[STIX]{x1D703}^{\prime }:\mathbb{T}_{h}^{\prime }\rightarrow \mathbb{J}^{\circ }$
be the family given by Corollary 5.10. We identify
$\unicode[STIX]{x1D703}^{\prime }:\mathbb{T}_{h}^{\prime }\rightarrow \mathbb{J}^{\circ }$
be the family given by Corollary 5.10. We identify
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
with
$\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
with
![]() $\mathbb{J}_{\operatorname{Tr}}^{\circ }$
via the isomorphism
$\mathbb{J}_{\operatorname{Tr}}^{\circ }$
via the isomorphism
![]() $\unicode[STIX]{x1D6FC}$
given by the same corollary; in particular, the Galois representation associated with
$\unicode[STIX]{x1D6FC}$
given by the same corollary; in particular, the Galois representation associated with
![]() $\unicode[STIX]{x1D703}^{\prime }$
is
$\unicode[STIX]{x1D703}^{\prime }$
is
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}=\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6F4}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime })$
.
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}=\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D6F4}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime })$
.
Recall that we are working under the assumptions of Proposition 5.4. In particular, we are given two primes
![]() $\mathfrak{P}_{i}$
and
$\mathfrak{P}_{i}$
and
![]() $\mathfrak{P}_{j}$
of
$\mathfrak{P}_{j}$
of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
, an isomorphism
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
, an isomorphism
![]() $\unicode[STIX]{x1D70E}:\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j}$
and a character
$\unicode[STIX]{x1D70E}:\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{i}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j}$
and a character
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j})^{\times }$
such that
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow (\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P}_{j})^{\times }$
such that
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{P}_{i}}^{\unicode[STIX]{x1D70E}}\cong \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}\otimes \unicode[STIX]{x1D70C}_{\mathfrak{ P}_{j}}$
. Let
$\unicode[STIX]{x1D70C}_{\mathfrak{P}_{i}}^{\unicode[STIX]{x1D70E}}\cong \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}\otimes \unicode[STIX]{x1D70C}_{\mathfrak{ P}_{j}}$
. Let
![]() $\mathfrak{P}_{i}^{\prime }$
be the image of
$\mathfrak{P}_{i}^{\prime }$
be the image of
![]() $\mathfrak{P}_{i}$
via the map
$\mathfrak{P}_{i}$
via the map
![]() $\unicode[STIX]{x1D704}_{h}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
. The specialization of
$\unicode[STIX]{x1D704}_{h}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
. The specialization of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{M^{\prime }}}$
at
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{M^{\prime }}}$
at
![]() $\mathfrak{P}_{i}^{\prime }$
is
$\mathfrak{P}_{i}^{\prime }$
is
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{P}_{i}}$
. Let
$\unicode[STIX]{x1D70C}_{\mathfrak{P}_{i}}$
. Let
![]() $f^{\prime }$
be an eigenform corresponding to
$f^{\prime }$
be an eigenform corresponding to
![]() $\mathfrak{P}_{i}^{\prime }$
. By Remark 5.9, there is a point of the family
$\mathfrak{P}_{i}^{\prime }$
. By Remark 5.9, there is a point of the family
![]() $\unicode[STIX]{x1D703}^{\prime }$
corresponding to the twist of
$\unicode[STIX]{x1D703}^{\prime }$
corresponding to the twist of
![]() $f$
by
$f$
by
![]() $\unicode[STIX]{x1D702}$
; let
$\unicode[STIX]{x1D702}$
; let
![]() $\mathfrak{P}_{i,\unicode[STIX]{x1D702}}^{\prime }$
be the prime of
$\mathfrak{P}_{i,\unicode[STIX]{x1D702}}^{\prime }$
be the prime of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
defining this point. The specialization of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,\unicode[STIX]{x1D6EC}_{h}^{\prime }$
defining this point. The specialization of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}$
at
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}$
at
![]() $\mathfrak{P}_{i,\unicode[STIX]{x1D702}}^{\prime }$
is
$\mathfrak{P}_{i,\unicode[STIX]{x1D702}}^{\prime }$
is
![]() $\unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D70C}_{\mathfrak{P}_{i}}$
, which is isomorphic to
$\unicode[STIX]{x1D702}\otimes \unicode[STIX]{x1D70C}_{\mathfrak{P}_{i}}$
, which is isomorphic to
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{P}_{i}}^{\unicode[STIX]{x1D70E}}$
by assumption. Let
$\unicode[STIX]{x1D70C}_{\mathfrak{P}_{i}}^{\unicode[STIX]{x1D70E}}$
by assumption. Let
![]() $f_{\unicode[STIX]{x1D702}}^{\prime }$
be an eigenform corresponding to the prime
$f_{\unicode[STIX]{x1D702}}^{\prime }$
be an eigenform corresponding to the prime
![]() $\mathfrak{P}_{i,\unicode[STIX]{x1D702}}^{\prime }$
. The forms
$\mathfrak{P}_{i,\unicode[STIX]{x1D702}}^{\prime }$
. The forms
![]() $f^{\prime }$
and
$f^{\prime }$
and
![]() $f_{\unicode[STIX]{x1D702}}^{\prime }$
have the same slope by Proposition 5.7 and their associated representations are obtained from one another via Galois conjugation (given by the isomorphism
$f_{\unicode[STIX]{x1D702}}^{\prime }$
have the same slope by Proposition 5.7 and their associated representations are obtained from one another via Galois conjugation (given by the isomorphism
![]() $\unicode[STIX]{x1D70E}$
). Hence,
$\unicode[STIX]{x1D70E}$
). Hence,
![]() $f^{\prime }$
and
$f^{\prime }$
and
![]() $f_{\unicode[STIX]{x1D702}}^{\prime }$
define the same point of the eigenvariety
$f_{\unicode[STIX]{x1D702}}^{\prime }$
define the same point of the eigenvariety
![]() ${\mathcal{D}}_{2}^{M^{\prime }}$
. Such a point belongs to both the families
${\mathcal{D}}_{2}^{M^{\prime }}$
. Such a point belongs to both the families
![]() $\unicode[STIX]{x1D703}^{M^{\prime }}$
and
$\unicode[STIX]{x1D703}^{M^{\prime }}$
and
![]() $\unicode[STIX]{x1D703}^{\prime }$
. As
$\unicode[STIX]{x1D703}^{\prime }$
. As
![]() $\mathfrak{P}_{\text{}\underline{k}}$
is non-critical,
$\mathfrak{P}_{\text{}\underline{k}}$
is non-critical,
![]() $\mathbb{T}_{h}^{\prime }$
is étale at every point lying over
$\mathbb{T}_{h}^{\prime }$
is étale at every point lying over
![]() $P_{\text{}\underline{k}}$
, so the families
$P_{\text{}\underline{k}}$
, so the families
![]() $\unicode[STIX]{x1D703}^{M^{\prime }}$
and
$\unicode[STIX]{x1D703}^{M^{\prime }}$
and
![]() $\unicode[STIX]{x1D703}^{\prime }$
must coincide. This means that there is an isomorphism
$\unicode[STIX]{x1D703}^{\prime }$
must coincide. This means that there is an isomorphism
such that
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}=\widetilde{\unicode[STIX]{x1D70E}}^{\prime }\circ \,\unicode[STIX]{x1D70C}^{M^{\prime }}$
. The isomorphism
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }}=\widetilde{\unicode[STIX]{x1D70E}}^{\prime }\circ \,\unicode[STIX]{x1D70C}^{M^{\prime }}$
. The isomorphism
![]() $\widetilde{\unicode[STIX]{x1D70E}}^{\prime }$
induces by restriction an isomorphism
$\widetilde{\unicode[STIX]{x1D70E}}^{\prime }$
induces by restriction an isomorphism
![]() $\unicode[STIX]{x1D6EC}_{h}^{\prime }[\operatorname{Tr}(\unicode[STIX]{x1D70C}^{M^{\prime }})]\rightarrow \unicode[STIX]{x1D6EC}_{h}^{\prime }[\operatorname{Tr}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }})]$
. Note that
$\unicode[STIX]{x1D6EC}_{h}^{\prime }[\operatorname{Tr}(\unicode[STIX]{x1D70C}^{M^{\prime }})]\rightarrow \unicode[STIX]{x1D6EC}_{h}^{\prime }[\operatorname{Tr}(\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}^{\prime }})]$
. Note that
![]() $\unicode[STIX]{x1D6EC}_{h}^{\prime }[\operatorname{Tr}(\unicode[STIX]{x1D70C}^{M^{\prime }})]=\unicode[STIX]{x1D704}_{h}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
and
$\unicode[STIX]{x1D6EC}_{h}^{\prime }[\operatorname{Tr}(\unicode[STIX]{x1D70C}^{M^{\prime }})]=\unicode[STIX]{x1D704}_{h}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
and
In particular,
![]() $\widetilde{\unicode[STIX]{x1D70E}}^{\prime }$
induces by restriction an isomorphism
$\widetilde{\unicode[STIX]{x1D70E}}^{\prime }$
induces by restriction an isomorphism
![]() $\unicode[STIX]{x1D704}_{h}(\mathbb{I}_{\operatorname{Tr}}^{\circ })\cong \unicode[STIX]{x1D704}_{h}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. As
$\unicode[STIX]{x1D704}_{h}(\mathbb{I}_{\operatorname{Tr}}^{\circ })\cong \unicode[STIX]{x1D704}_{h}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. As
![]() $\unicode[STIX]{x1D704}_{h}$
is injective, we can identify
$\unicode[STIX]{x1D704}_{h}$
is injective, we can identify
![]() $\widetilde{\unicode[STIX]{x1D70E}}^{\prime }$
with an isomorphism
$\widetilde{\unicode[STIX]{x1D70E}}^{\prime }$
with an isomorphism
![]() $\widetilde{\unicode[STIX]{x1D70E}}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. By construction,
$\widetilde{\unicode[STIX]{x1D70E}}:\mathbb{I}_{\operatorname{Tr}}^{\circ }\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. By construction,
![]() $\widetilde{\unicode[STIX]{x1D70E}}$
fits in diagram (10).◻
$\widetilde{\unicode[STIX]{x1D70E}}$
fits in diagram (10).◻
5.2 Rings of conjugate self-twists for representations attached to classical eigenforms
Let
![]() $f$
be a classical
$f$
be a classical
![]() $\operatorname{GSp}_{4}$
-eigenform and
$\operatorname{GSp}_{4}$
-eigenform and
![]() $\unicode[STIX]{x1D70C}_{f,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\overline{\mathbb{Q}}_{p})$
the
$\unicode[STIX]{x1D70C}_{f,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\overline{\mathbb{Q}}_{p})$
the
![]() $p$
-adic Galois representation associated with
$p$
-adic Galois representation associated with
![]() $f$
. Up to replacing
$f$
. Up to replacing
![]() $\unicode[STIX]{x1D70C}_{f,p}$
with a conjugate we can suppose that it has coefficients in the ring of integers
$\unicode[STIX]{x1D70C}_{f,p}$
with a conjugate we can suppose that it has coefficients in the ring of integers
![]() ${\mathcal{O}}_{K}$
of a
${\mathcal{O}}_{K}$
of a
![]() $p$
-adic field
$p$
-adic field
![]() $K$
. Suppose that
$K$
. Suppose that
![]() $f$
satisfies the hypotheses of Theorem 3.12, i.e. that
$f$
satisfies the hypotheses of Theorem 3.12, i.e. that
![]() $\overline{\unicode[STIX]{x1D70C}}_{f,p}$
is of
$\overline{\unicode[STIX]{x1D70C}}_{f,p}$
is of
![]() $\operatorname{Sym}^{3}$
type, but
$\operatorname{Sym}^{3}$
type, but
![]() $f$
is not the symmetric cube lift of a
$f$
is not the symmetric cube lift of a
![]() $\operatorname{GL}_{2}$
-eigenform. Let
$\operatorname{GL}_{2}$
-eigenform. Let
![]() $\unicode[STIX]{x1D6E4}_{f}$
be the group of conjugate self-twists for
$\unicode[STIX]{x1D6E4}_{f}$
be the group of conjugate self-twists for
![]() $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
![]() $\mathbb{Z}_{p}$
and let
$\mathbb{Z}_{p}$
and let
![]() ${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
be the subring of elements of
${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
be the subring of elements of
![]() ${\mathcal{O}}_{K}$
fixed by
${\mathcal{O}}_{K}$
fixed by
![]() $\unicode[STIX]{x1D6E4}_{f}$
. As in §3.3, we define another subring of
$\unicode[STIX]{x1D6E4}_{f}$
. As in §3.3, we define another subring of
![]() ${\mathcal{O}}_{K}$
by
${\mathcal{O}}_{K}$
by
![]() ${\mathcal{O}}_{E}=\mathbb{Z}_{p}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})]$
. We prove the following.
${\mathcal{O}}_{E}=\mathbb{Z}_{p}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})]$
. We prove the following.
Proposition 5.11. There is an equality
![]() ${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}={\mathcal{O}}_{E}$
.
${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}={\mathcal{O}}_{E}$
.
Before proving Proposition 5.11, we recall a result of O’Meara about isomorphisms of congruence subgroups. We denote by
![]() $\operatorname{PSp}_{2g}$
and
$\operatorname{PSp}_{2g}$
and
![]() $\operatorname{PGSp}_{2g}$
the projective symplectic groups of genus
$\operatorname{PGSp}_{2g}$
the projective symplectic groups of genus
![]() $g$
. The following is a rewriting of [Reference O’MearaOMe78, Theorem 5.6.4] for the situation we are interested in.
$g$
. The following is a rewriting of [Reference O’MearaOMe78, Theorem 5.6.4] for the situation we are interested in.
Theorem 5.12. Let
![]() $F$
and
$F$
and
![]() $F_{1}$
be two fields. Let
$F_{1}$
be two fields. Let
![]() $\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}$
and
![]() $\unicode[STIX]{x1D6E5}_{1}$
be subgroups of
$\unicode[STIX]{x1D6E5}_{1}$
be subgroups of
![]() $\operatorname{PGSp}_{2g}(F)$
and
$\operatorname{PGSp}_{2g}(F)$
and
![]() $\operatorname{PGSp}_{2g}(F_{1})$
, respectively, satisfying
$\operatorname{PGSp}_{2g}(F_{1})$
, respectively, satisfying
![]() $\unicode[STIX]{x1D6E4}_{\operatorname{PSp}_{2g}(F)}(\mathfrak{a})\subset \unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E4}_{\operatorname{PSp}_{2g}(F)}(\mathfrak{a})\subset \unicode[STIX]{x1D6E5}$
and
![]() $\unicode[STIX]{x1D6E4}_{\operatorname{PSp}_{2g}(F_{1})}(\mathfrak{a})\subset \unicode[STIX]{x1D6E5}_{1}$
. Let
$\unicode[STIX]{x1D6E4}_{\operatorname{PSp}_{2g}(F_{1})}(\mathfrak{a})\subset \unicode[STIX]{x1D6E5}_{1}$
. Let
![]() $\unicode[STIX]{x1D6E9}:\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E5}_{1}$
be an isomorphism of groups. Then there exists an automorphism
$\unicode[STIX]{x1D6E9}:\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E5}_{1}$
be an isomorphism of groups. Then there exists an automorphism
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $F$
and an element
$F$
and an element
![]() $\unicode[STIX]{x1D6FE}\in \operatorname{PGSp}_{2g}(F_{1})$
satisfying
$\unicode[STIX]{x1D6FE}\in \operatorname{PGSp}_{2g}(F_{1})$
satisfying
for every
![]() $x\in \unicode[STIX]{x1D6E5}$
.
$x\in \unicode[STIX]{x1D6E5}$
.
We fix some notation. Let
![]() $\operatorname{End}(\mathfrak{s}\mathfrak{p}_{4}(K))$
be the
$\operatorname{End}(\mathfrak{s}\mathfrak{p}_{4}(K))$
be the
![]() $K$
-vector space of
$K$
-vector space of
![]() $K$
-linear maps
$K$
-linear maps
![]() $\mathfrak{s}\mathfrak{p}_{4}(K)\rightarrow \mathfrak{s}\mathfrak{p}_{4}(K)$
and let
$\mathfrak{s}\mathfrak{p}_{4}(K)\rightarrow \mathfrak{s}\mathfrak{p}_{4}(K)$
and let
![]() $\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
be the subgroup consisting of the bijective ones. Let
$\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
be the subgroup consisting of the bijective ones. Let
![]() $\operatorname{Aut}(\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(K))$
be the subgroup of
$\operatorname{Aut}(\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(K))$
be the subgroup of
![]() $\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
consisting of the Lie algebra automorphisms of
$\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
consisting of the Lie algebra automorphisms of
![]() $\mathfrak{s}\mathfrak{p}_{4}(K)$
. Let
$\mathfrak{s}\mathfrak{p}_{4}(K)$
. Let
![]() $\unicode[STIX]{x1D70B}_{\operatorname{Ad}}$
be the natural projection
$\unicode[STIX]{x1D70B}_{\operatorname{Ad}}$
be the natural projection
![]() $\operatorname{GSp}_{4}({\mathcal{O}}_{K})\rightarrow \operatorname{PGSp}_{4}({\mathcal{O}}_{K})$
and let
$\operatorname{GSp}_{4}({\mathcal{O}}_{K})\rightarrow \operatorname{PGSp}_{4}({\mathcal{O}}_{K})$
and let
![]() $\operatorname{Ad}:\operatorname{PGSp}_{4}(K){\hookrightarrow}\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
be the injective group morphism defined by the adjoint representation. As
$\operatorname{Ad}:\operatorname{PGSp}_{4}(K){\hookrightarrow}\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
be the injective group morphism defined by the adjoint representation. As
![]() $\mathfrak{s}\mathfrak{p}_{4}$
admits no outer automorphisms,
$\mathfrak{s}\mathfrak{p}_{4}$
admits no outer automorphisms,
![]() $\operatorname{Ad}$
induces an isomorphism
$\operatorname{Ad}$
induces an isomorphism
![]() $\operatorname{PGSp}_{4}(K)\cong \operatorname{Aut}(\mathfrak{s}\mathfrak{p}_{4}(K))$
. For simplicity, we write
$\operatorname{PGSp}_{4}(K)\cong \operatorname{Aut}(\mathfrak{s}\mathfrak{p}_{4}(K))$
. For simplicity, we write
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{f,p}$
in the following proof (but recall that in the other sections
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{f,p}$
in the following proof (but recall that in the other sections
![]() $\unicode[STIX]{x1D70C}$
is the Galois representation attached to a family).
$\unicode[STIX]{x1D70C}$
is the Galois representation attached to a family).
Proof of Proposition 5.11.
The inclusion
![]() ${\mathcal{O}}_{E}\subset {\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
follows from Proposition 5.2(5). We prove that
${\mathcal{O}}_{E}\subset {\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
follows from Proposition 5.2(5). We prove that
![]() ${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}\subset {\mathcal{O}}_{E}$
. As
${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}\subset {\mathcal{O}}_{E}$
. As
![]() ${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
and
${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
and
![]() ${\mathcal{O}}_{E}$
are normal, it is sufficient to show that an automorphism of
${\mathcal{O}}_{E}$
are normal, it is sufficient to show that an automorphism of
![]() ${\mathcal{O}}_{K}$
over
${\mathcal{O}}_{K}$
over
![]() ${\mathcal{O}}_{E}$
leaves
${\mathcal{O}}_{E}$
leaves
![]() ${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
fixed. Consider such an automorphism
${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
fixed. Consider such an automorphism
![]() $\unicode[STIX]{x1D70E}$
. As
$\unicode[STIX]{x1D70E}$
. As
![]() ${\mathcal{O}}_{E}$
is fixed by
${\mathcal{O}}_{E}$
is fixed by
![]() $\unicode[STIX]{x1D70E}$
, we have
$\unicode[STIX]{x1D70E}$
, we have
![]() $(\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})(g))^{\unicode[STIX]{x1D70E}}=\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C}(g))$
for every
$(\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})(g))^{\unicode[STIX]{x1D70E}}=\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C}(g))$
for every
![]() $g\in G_{\mathbb{Q}}$
, hence
$g\in G_{\mathbb{Q}}$
, hence
![]() $\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}(g))=\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C}(g))$
. The equality of traces induces an isomorphism
$\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}(g))=\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C}(g))$
. The equality of traces induces an isomorphism
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}\cong \operatorname{Ad}\unicode[STIX]{x1D70C}$
of representations of
$\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}\cong \operatorname{Ad}\unicode[STIX]{x1D70C}$
of representations of
![]() $G_{\mathbb{Q}}$
with values in
$G_{\mathbb{Q}}$
with values in
![]() $\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4})$
. This means that there exists
$\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4})$
. This means that there exists
![]() $\unicode[STIX]{x1D719}\in \operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
satisfying
$\unicode[STIX]{x1D719}\in \operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
satisfying
We show that
![]() $\unicode[STIX]{x1D719}$
is actually an inner automorphism of
$\unicode[STIX]{x1D719}$
is actually an inner automorphism of
![]() $\mathfrak{s}\mathfrak{p}_{4}(K)$
.
$\mathfrak{s}\mathfrak{p}_{4}(K)$
.
Clearly
![]() $\operatorname{Ad}$
induces an isomorphism
$\operatorname{Ad}$
induces an isomorphism
![]() $\unicode[STIX]{x1D70B}_{\operatorname{Ad}}(\operatorname{Im}\unicode[STIX]{x1D70C})\cong \operatorname{Im}\operatorname{Ad}\unicode[STIX]{x1D70C}$
. For every
$\unicode[STIX]{x1D70B}_{\operatorname{Ad}}(\operatorname{Im}\unicode[STIX]{x1D70C})\cong \operatorname{Im}\operatorname{Ad}\unicode[STIX]{x1D70C}$
. For every
![]() $x\in \operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
, we denote by
$x\in \operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
, we denote by
![]() $\unicode[STIX]{x1D6E9}_{x}$
the automorphism of
$\unicode[STIX]{x1D6E9}_{x}$
the automorphism of
![]() $\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
given by conjugation by
$\operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4}(K))$
given by conjugation by
![]() $x$
. In particular, we write (11) as
$x$
. In particular, we write (11) as
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(\operatorname{Ad}\unicode[STIX]{x1D70C})$
. By combining Theorems 3.12 and 5.12, we show that we can replace
$\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(\operatorname{Ad}\unicode[STIX]{x1D70C})$
. By combining Theorems 3.12 and 5.12, we show that we can replace
![]() $\unicode[STIX]{x1D719}$
by an element
$\unicode[STIX]{x1D719}$
by an element
![]() $\unicode[STIX]{x1D719}^{\prime }\in \operatorname{Aut}(\mathfrak{s}\mathfrak{p}_{4}(K))$
still satisfying
$\unicode[STIX]{x1D719}^{\prime }\in \operatorname{Aut}(\mathfrak{s}\mathfrak{p}_{4}(K))$
still satisfying
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}^{\prime }}(\operatorname{Ad}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719}^{\prime }))$
.
$\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}^{\prime }}(\operatorname{Ad}\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D719}^{\prime }))$
.
We identify
![]() $\operatorname{PGSp}_{4}({\mathcal{O}}_{E})$
with a subgroup of
$\operatorname{PGSp}_{4}({\mathcal{O}}_{E})$
with a subgroup of
![]() $\operatorname{PGSp}_{4}({\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}})$
via the inclusion
$\operatorname{PGSp}_{4}({\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}})$
via the inclusion
![]() ${\mathcal{O}}_{E}\subset {\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
given in the beginning of the proof. Consider the group
${\mathcal{O}}_{E}\subset {\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
given in the beginning of the proof. Consider the group
![]() $\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D70B}_{\operatorname{Ad}}\operatorname{Im}\unicode[STIX]{x1D70C})\cap \operatorname{PGSp}_{4}({\mathcal{O}}_{E})\subset \operatorname{PGSp}_{4}({\mathcal{O}}_{K})$
and its isomorphic image
$\unicode[STIX]{x1D6E5}=(\unicode[STIX]{x1D70B}_{\operatorname{Ad}}\operatorname{Im}\unicode[STIX]{x1D70C})\cap \operatorname{PGSp}_{4}({\mathcal{O}}_{E})\subset \operatorname{PGSp}_{4}({\mathcal{O}}_{K})$
and its isomorphic image
![]() $\operatorname{Ad}(\unicode[STIX]{x1D6E5})\subset \operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4})$
. As
$\operatorname{Ad}(\unicode[STIX]{x1D6E5})\subset \operatorname{GL}(\mathfrak{s}\mathfrak{p}_{4})$
. As
![]() $f$
satisfies the hypotheses of Theorem 3.12,
$f$
satisfies the hypotheses of Theorem 3.12,
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}$
contains a congruence subgroup
$\operatorname{Im}\unicode[STIX]{x1D70C}$
contains a congruence subgroup
![]() $\unicode[STIX]{x1D6E4}_{{\mathcal{O}}_{E}}(\mathfrak{a})$
of
$\unicode[STIX]{x1D6E4}_{{\mathcal{O}}_{E}}(\mathfrak{a})$
of
![]() $\operatorname{GSp}_{4}({\mathcal{O}}_{E})$
of some level
$\operatorname{GSp}_{4}({\mathcal{O}}_{E})$
of some level
![]() $\mathfrak{a}\subset {\mathcal{O}}_{E}$
. It follows that
$\mathfrak{a}\subset {\mathcal{O}}_{E}$
. It follows that
![]() $\unicode[STIX]{x1D70B}_{\operatorname{Ad}}\operatorname{Im}\unicode[STIX]{x1D70C}$
contains the projective congruence subgroup
$\unicode[STIX]{x1D70B}_{\operatorname{Ad}}\operatorname{Im}\unicode[STIX]{x1D70C}$
contains the projective congruence subgroup
![]() $\text{P}\unicode[STIX]{x1D6E4}_{{\mathcal{O}}_{E}}(\mathfrak{a})$
of
$\text{P}\unicode[STIX]{x1D6E4}_{{\mathcal{O}}_{E}}(\mathfrak{a})$
of
![]() $\operatorname{PGSp}_{4}({\mathcal{O}}_{E})$
, so
$\operatorname{PGSp}_{4}({\mathcal{O}}_{E})$
, so
![]() $\unicode[STIX]{x1D6E5}$
also contains
$\unicode[STIX]{x1D6E5}$
also contains
![]() $\text{P}\unicode[STIX]{x1D6E4}_{{\mathcal{O}}_{E}}(\mathfrak{a})$
. In particular,
$\text{P}\unicode[STIX]{x1D6E4}_{{\mathcal{O}}_{E}}(\mathfrak{a})$
. In particular,
![]() $\unicode[STIX]{x1D6E5}$
satisfies the hypotheses of Theorem 5.12. As
$\unicode[STIX]{x1D6E5}$
satisfies the hypotheses of Theorem 5.12. As
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(\operatorname{Ad}\unicode[STIX]{x1D70C})$
, we have an equality
$\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(\operatorname{Ad}\unicode[STIX]{x1D70C})$
, we have an equality
![]() $(\operatorname{Ad}(\unicode[STIX]{x1D6E5}))^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(\operatorname{Ad}(\unicode[STIX]{x1D6E5}))$
, where we identify both sides with subgroups of
$(\operatorname{Ad}(\unicode[STIX]{x1D6E5}))^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(\operatorname{Ad}(\unicode[STIX]{x1D6E5}))$
, where we identify both sides with subgroups of
![]() $\operatorname{PGSp}_{4}({\mathcal{O}}_{E})$
. Now
$\operatorname{PGSp}_{4}({\mathcal{O}}_{E})$
. Now
![]() $\unicode[STIX]{x1D70E}$
acts as the identity on
$\unicode[STIX]{x1D70E}$
acts as the identity on
![]() $\operatorname{PGSp}_{4}({\mathcal{O}}_{E})$
, so the previous equality reduces to
$\operatorname{PGSp}_{4}({\mathcal{O}}_{E})$
, so the previous equality reduces to
![]() $\operatorname{Ad}(\unicode[STIX]{x1D6E5})=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(\operatorname{Ad}(\unicode[STIX]{x1D6E5}))$
. Let
$\operatorname{Ad}(\unicode[STIX]{x1D6E5})=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(\operatorname{Ad}(\unicode[STIX]{x1D6E5}))$
. Let
![]() $\unicode[STIX]{x1D6E9}=\operatorname{Ad}\!^{-1}\circ \,\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}\circ \,\operatorname{Ad}\!:\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E5}$
. As
$\unicode[STIX]{x1D6E9}=\operatorname{Ad}\!^{-1}\circ \,\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}\circ \,\operatorname{Ad}\!:\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E5}$
. As
![]() $\operatorname{Ad}$
is an isomorphism, the composition
$\operatorname{Ad}$
is an isomorphism, the composition
![]() $\unicode[STIX]{x1D6E9}$
is an automorphism. Moreover, it satisfies
$\unicode[STIX]{x1D6E9}$
is an automorphism. Moreover, it satisfies
for every
![]() $\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
. By Theorem 5.12 applied to
$\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
. By Theorem 5.12 applied to
![]() $F=F_{1}=K$
,
$F=F_{1}=K$
,
![]() $\unicode[STIX]{x1D6E5}_{1}=\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}_{1}=\unicode[STIX]{x1D6E5}$
and
![]() $\unicode[STIX]{x1D6E9}:\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E5}$
, there exists an automorphism
$\unicode[STIX]{x1D6E9}:\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6E5}$
, there exists an automorphism
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $K$
and an element
$K$
and an element
![]() $\unicode[STIX]{x1D6FE}\in \operatorname{GSp}_{4}(K)$
such that
$\unicode[STIX]{x1D6FE}\in \operatorname{GSp}_{4}(K)$
such that
![]() $\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FE}^{-1}$
for every
$\unicode[STIX]{x1D6E9}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FF}^{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6FE}^{-1}$
for every
![]() $\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
. We see from (12) that
$\unicode[STIX]{x1D6FF}\in \unicode[STIX]{x1D6E5}$
. We see from (12) that
![]() $\unicode[STIX]{x1D70F}$
is trivial. It follows that
$\unicode[STIX]{x1D70F}$
is trivial. It follows that
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(y)=\operatorname{Ad}(\unicode[STIX]{x1D6FE})\circ \,y\circ \,\operatorname{Ad}(\unicode[STIX]{x1D6FE})^{-1}$
for all
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}(y)=\operatorname{Ad}(\unicode[STIX]{x1D6FE})\circ \,y\circ \,\operatorname{Ad}(\unicode[STIX]{x1D6FE})^{-1}$
for all
![]() $y\in \operatorname{Ad}(\unicode[STIX]{x1D6E5})$
. By
$y\in \operatorname{Ad}(\unicode[STIX]{x1D6E5})$
. By
![]() $K$
-linearity, we can extend
$K$
-linearity, we can extend
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}$
and
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}$
and
![]() $\unicode[STIX]{x1D6E9}_{\operatorname{Ad}(\unicode[STIX]{x1D6FE})}$
to identical automorphisms of the
$\unicode[STIX]{x1D6E9}_{\operatorname{Ad}(\unicode[STIX]{x1D6FE})}$
to identical automorphisms of the
![]() $K$
-span of
$K$
-span of
![]() $\operatorname{Ad}(\unicode[STIX]{x1D6E5})$
in
$\operatorname{Ad}(\unicode[STIX]{x1D6E5})$
in
![]() $\operatorname{End}(\mathfrak{s}\mathfrak{p}_{4}(K))$
. As
$\operatorname{End}(\mathfrak{s}\mathfrak{p}_{4}(K))$
. As
![]() $\unicode[STIX]{x1D6E5}$
contains the projective congruence subgroup
$\unicode[STIX]{x1D6E5}$
contains the projective congruence subgroup
![]() $\text{P}\unicode[STIX]{x1D6E4}_{{\mathcal{O}}_{E}}(\mathfrak{a})$
, its
$\text{P}\unicode[STIX]{x1D6E4}_{{\mathcal{O}}_{E}}(\mathfrak{a})$
, its
![]() $K$
-span contains
$K$
-span contains
![]() $\operatorname{Ad}(\operatorname{GSp}_{4}(K))$
; in particular, it contains the image of
$\operatorname{Ad}(\operatorname{GSp}_{4}(K))$
; in particular, it contains the image of
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}$
. Hence,
$\operatorname{Ad}\unicode[STIX]{x1D70C}$
. Hence,
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}$
and
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D719}}$
and
![]() $\unicode[STIX]{x1D6E9}_{\operatorname{Ad}(\unicode[STIX]{x1D6FE})}$
agree on
$\unicode[STIX]{x1D6E9}_{\operatorname{Ad}(\unicode[STIX]{x1D6FE})}$
agree on
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}$
, which means that (11) implies
$\operatorname{Ad}\unicode[STIX]{x1D70C}$
, which means that (11) implies
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\operatorname{Ad}(\unicode[STIX]{x1D6FE})}(\operatorname{Ad}\unicode[STIX]{x1D70C})$
. Then, by the definition of
$\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D6E9}_{\operatorname{Ad}(\unicode[STIX]{x1D6FE})}(\operatorname{Ad}\unicode[STIX]{x1D70C})$
. Then, by the definition of
![]() $\unicode[STIX]{x1D6E9}_{\operatorname{Ad}(\unicode[STIX]{x1D6FE})}$
, we have
$\unicode[STIX]{x1D6E9}_{\operatorname{Ad}(\unicode[STIX]{x1D6FE})}$
, we have
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\operatorname{Ad}(\unicode[STIX]{x1D6FE})\circ \,\operatorname{Ad}\unicode[STIX]{x1D70C}\circ \,(\operatorname{Ad}(\unicode[STIX]{x1D6FE}))^{-1}=\operatorname{Ad}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}^{-1})$
. We deduce that there exists a character
$\operatorname{Ad}\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}=\operatorname{Ad}(\unicode[STIX]{x1D6FE})\circ \,\operatorname{Ad}\unicode[STIX]{x1D70C}\circ \,(\operatorname{Ad}(\unicode[STIX]{x1D6FE}))^{-1}=\operatorname{Ad}(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}^{-1})$
. We deduce that there exists a character
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}_{K}^{\times }$
satisfying
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}_{K}^{\times }$
satisfying
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}(g)=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}(g)\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70C}(g)\unicode[STIX]{x1D6FE}^{-1}$
for every
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}(g)=\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}(g)\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D70C}(g)\unicode[STIX]{x1D6FE}^{-1}$
for every
![]() $g\in G_{\mathbb{Q}}$
, hence that
$g\in G_{\mathbb{Q}}$
, hence that
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}\cong \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}\otimes \unicode[STIX]{x1D70C}$
. We conclude that
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}\cong \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}\otimes \unicode[STIX]{x1D70C}$
. We conclude that
![]() $\unicode[STIX]{x1D70E}$
is a conjugate self-twist for
$\unicode[STIX]{x1D70E}$
is a conjugate self-twist for
![]() $\unicode[STIX]{x1D70C}$
. In particular,
$\unicode[STIX]{x1D70C}$
. In particular,
![]() $\unicode[STIX]{x1D70E}$
acts as the identity on
$\unicode[STIX]{x1D70E}$
acts as the identity on
![]() ${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
, as desired.◻
${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
, as desired.◻
Remark 5.13. Let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the big Galois representation associated with a family
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the big Galois representation associated with a family
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
. We can define a ring
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
. We can define a ring
![]() $\unicode[STIX]{x1D6EC}_{h}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})]$
analogous to the ring
$\unicode[STIX]{x1D6EC}_{h}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})]$
analogous to the ring
![]() ${\mathcal{O}}_{E}$
defined above. We have an inclusion
${\mathcal{O}}_{E}$
defined above. We have an inclusion
![]() $\unicode[STIX]{x1D6EC}_{h}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})]\subset \mathbb{I}_{0}^{\circ }$
given by Proposition 5.2(5). However, the proof of the inclusion
$\unicode[STIX]{x1D6EC}_{h}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})]\subset \mathbb{I}_{0}^{\circ }$
given by Proposition 5.2(5). However, the proof of the inclusion
![]() ${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}\subset {\mathcal{O}}_{E}$
in Proposition 5.11 relied on the fact that
${\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}\subset {\mathcal{O}}_{E}$
in Proposition 5.11 relied on the fact that
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{f,p}$
contains a congruence subgroup of
$\operatorname{Im}\unicode[STIX]{x1D70C}_{f,p}$
contains a congruence subgroup of
![]() $\operatorname{GSp}_{4}({\mathcal{O}}_{E})$
. As we do not know if an analogue for
$\operatorname{GSp}_{4}({\mathcal{O}}_{E})$
. As we do not know if an analogue for
![]() $\unicode[STIX]{x1D70C}$
is true, we do not know whether an equality between the normalizations of
$\unicode[STIX]{x1D70C}$
is true, we do not know whether an equality between the normalizations of
![]() $\unicode[STIX]{x1D6EC}_{h}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})]$
and
$\unicode[STIX]{x1D6EC}_{h}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C})]$
and
![]() $\mathbb{I}_{0}^{\circ }$
holds.
$\mathbb{I}_{0}^{\circ }$
holds.
Suppose that the
![]() $\operatorname{GSp}_{4}$
-eigenform
$\operatorname{GSp}_{4}$
-eigenform
![]() $f$
appears in a finite slope family
$f$
appears in a finite slope family
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
. Let
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
. Let
![]() $\mathfrak{P}$
be the prime of
$\mathfrak{P}$
be the prime of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
associated with
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
associated with
![]() $f$
and suppose that
$f$
and suppose that
![]() $\mathfrak{P}\cap \unicode[STIX]{x1D6EC}_{h}$
is a non-critical arithmetic prime
$\mathfrak{P}\cap \unicode[STIX]{x1D6EC}_{h}$
is a non-critical arithmetic prime
![]() $P_{\text{}\underline{k}}$
. Let
$P_{\text{}\underline{k}}$
. Let
![]() $\mathfrak{P}_{0}=\mathfrak{P}\cap \mathbb{I}_{0}^{\circ }$
. The following is an analogue of [Reference LangLan16, Proposition 6.2], that results from a straightforward application of Corollary 5.5.
$\mathfrak{P}_{0}=\mathfrak{P}\cap \mathbb{I}_{0}^{\circ }$
. The following is an analogue of [Reference LangLan16, Proposition 6.2], that results from a straightforward application of Corollary 5.5.
Proposition 5.14. There is an inclusion
![]() $\mathbb{I}_{0}^{\circ }/\mathfrak{P}_{0}\subset {\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
.
$\mathbb{I}_{0}^{\circ }/\mathfrak{P}_{0}\subset {\mathcal{O}}_{K}^{\unicode[STIX]{x1D6E4}_{f}}$
.
The results of this section admit the following corollary.
Corollary 5.15. Let
![]() $\unicode[STIX]{x1D70C}\cong G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the representation associated with the family
$\unicode[STIX]{x1D70C}\cong G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the representation associated with the family
![]() $\unicode[STIX]{x1D703}$
. Let
$\unicode[STIX]{x1D703}$
. Let
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
corresponding to a classical eigenform
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
corresponding to a classical eigenform
![]() $f$
that is not a symmetric cube lift of a
$f$
that is not a symmetric cube lift of a
![]() $\operatorname{GL}_{2}$
-eigenform. Let
$\operatorname{GL}_{2}$
-eigenform. Let
![]() $\mathfrak{P}_{0}=\mathfrak{P}\cap \mathbb{I}_{0}^{\circ }$
. Then the image of
$\mathfrak{P}_{0}=\mathfrak{P}\cap \mathbb{I}_{0}^{\circ }$
. Then the image of
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{P}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P})$
contains a non-trivial congruence subgroup of
$\unicode[STIX]{x1D70C}_{\mathfrak{P}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P})$
contains a non-trivial congruence subgroup of
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{P}_{0})$
.
$\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{P}_{0})$
.
Proof. As before, let
![]() ${\mathcal{O}}_{E}=\mathbb{Z}_{p}[\operatorname{Tr}\operatorname{Ad}\unicode[STIX]{x1D70C}_{\mathfrak{P}}]$
. By Theorem 3.12, the image of
${\mathcal{O}}_{E}=\mathbb{Z}_{p}[\operatorname{Tr}\operatorname{Ad}\unicode[STIX]{x1D70C}_{\mathfrak{P}}]$
. By Theorem 3.12, the image of
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{P}}$
contains a congruence subgroup of
$\unicode[STIX]{x1D70C}_{\mathfrak{P}}$
contains a congruence subgroup of
![]() $\operatorname{GSp}_{4}({\mathcal{O}}_{E})$
. By combining Propositions 5.11 and 5.14, we obtain
$\operatorname{GSp}_{4}({\mathcal{O}}_{E})$
. By combining Propositions 5.11 and 5.14, we obtain
![]() $\mathbb{I}_{0}^{\circ }/\mathfrak{P}_{0}\subset {\mathcal{O}}_{E}$
, hence the corollary.◻
$\mathbb{I}_{0}^{\circ }/\mathfrak{P}_{0}\subset {\mathcal{O}}_{E}$
, hence the corollary.◻
6 Constructing bases of lattices in unipotent subgroups
In this section, we show that the image of the Galois representation associated with a family of
![]() $\operatorname{GSp}_{4}$
-eigenforms contains a ‘sufficiently large’ set of unipotent elements.
$\operatorname{GSp}_{4}$
-eigenforms contains a ‘sufficiently large’ set of unipotent elements.
6.1 An approximation argument
We recall a simple generalization of the approximation argument presented in the proof of [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, Lemma 4.5]. We refer to [Reference ContiCon16, §4.7] for the details of the proof, because there is an imprecision in the argument of [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15]. In particular, [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, Lemma 4.6] does not give the inclusion (4.3) in [Reference ContiCon16, §4.7]; it needs to be replaced by [Reference ContiCon16, Lemma 4.7.2]. Let
![]() $\mathbf{G}$
be a reductive group defined over
$\mathbf{G}$
be a reductive group defined over
![]() $\mathbb{Z}$
. Let
$\mathbb{Z}$
. Let
![]() $T$
and
$T$
and
![]() $B$
be a torus and a Borel subgroup of
$B$
be a torus and a Borel subgroup of
![]() $\mathbf{G}$
, respectively. Let
$\mathbf{G}$
, respectively. Let
![]() $\unicode[STIX]{x1D6E5}$
be the set of roots associated with
$\unicode[STIX]{x1D6E5}$
be the set of roots associated with
![]() $(\mathbf{G},T)$
.
$(\mathbf{G},T)$
.
Proposition 6.1 [Reference ContiCon16, Proposition 4.7.1].
Let
![]() $A$
be a profinite local ring of residual characteristic
$A$
be a profinite local ring of residual characteristic
![]() $p$
endowed with its profinite topology. Let
$p$
endowed with its profinite topology. Let
![]() $G$
be a compact subgroup of the level
$G$
be a compact subgroup of the level
![]() $p$
principal congruence subgroup
$p$
principal congruence subgroup
![]() $\unicode[STIX]{x1D6E4}_{\mathbf{G}(A)}(p)$
of
$\unicode[STIX]{x1D6E4}_{\mathbf{G}(A)}(p)$
of
![]() $\mathbf{G}(A)$
. Suppose that:
$\mathbf{G}(A)$
. Suppose that:
(i) the ring
 $A$
is complete with respect to the
$A$
is complete with respect to the
 $p$
-adic topology;
$p$
-adic topology;(ii) the group
 $G$
is normalized by a diagonal
$G$
is normalized by a diagonal
 $\mathbb{Z}_{p}$
-regular element of
$\mathbb{Z}_{p}$
-regular element of
 $\mathbf{G}(A)$
.
$\mathbf{G}(A)$
.
Let
![]() $\unicode[STIX]{x1D6FC}$
be a root of
$\unicode[STIX]{x1D6FC}$
be a root of
![]() $\mathbf{G}$
. For every ideal
$\mathbf{G}$
. For every ideal
![]() $Q$
of
$Q$
of
![]() $A$
, let
$A$
, let
![]() $\unicode[STIX]{x1D70B}_{Q}:\mathbf{G}(A)\rightarrow \mathbf{G}(A/Q)$
be the natural projection, inducing a map
$\unicode[STIX]{x1D70B}_{Q}:\mathbf{G}(A)\rightarrow \mathbf{G}(A/Q)$
be the natural projection, inducing a map
![]() $\unicode[STIX]{x1D70B}_{Q,\unicode[STIX]{x1D6FC}}:U^{\unicode[STIX]{x1D6FC}}(A)\rightarrow U^{\unicode[STIX]{x1D6FC}}(A/Q)$
. Then
$\unicode[STIX]{x1D70B}_{Q,\unicode[STIX]{x1D6FC}}:U^{\unicode[STIX]{x1D6FC}}(A)\rightarrow U^{\unicode[STIX]{x1D6FC}}(A/Q)$
. Then
![]() $\unicode[STIX]{x1D70B}_{Q}(G)\cap U^{\unicode[STIX]{x1D6FC}}(A/Q)=\unicode[STIX]{x1D70B}_{Q}(G\cap U^{\unicode[STIX]{x1D6FC}}(A))$
.
$\unicode[STIX]{x1D70B}_{Q}(G)\cap U^{\unicode[STIX]{x1D6FC}}(A/Q)=\unicode[STIX]{x1D70B}_{Q}(G\cap U^{\unicode[STIX]{x1D6FC}}(A))$
.
We give a simple corollary.
Corollary 6.2. Let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the Galois representation associated with a finite slope family
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the Galois representation associated with a finite slope family
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
. For every root
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
. For every root
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\operatorname{GSp}_{4}$
, the group
$\operatorname{GSp}_{4}$
, the group
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
is non-trivial.
$\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
is non-trivial.
Proof. Let
![]() $\mathfrak{P}$
be a prime of
$\mathfrak{P}$
be a prime of
![]() $\mathbb{I}^{\circ }$
corresponding to a classical eigenform
$\mathbb{I}^{\circ }$
corresponding to a classical eigenform
![]() $f$
that is not the symmetric cube lift of a
$f$
that is not the symmetric cube lift of a
![]() $\operatorname{GL}_{2}$
-eigenform. Let
$\operatorname{GL}_{2}$
-eigenform. Let
![]() ${\mathcal{O}}_{E}=\mathbb{Z}_{p}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C}_{\mathfrak{P}})]$
. By Theorem 3.12
${\mathcal{O}}_{E}=\mathbb{Z}_{p}[\operatorname{Tr}(\operatorname{Ad}\unicode[STIX]{x1D70C}_{\mathfrak{P}})]$
. By Theorem 3.12
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{\mathfrak{P}}$
contains a non-trivial congruence subgroup of
$\operatorname{Im}\unicode[STIX]{x1D70C}_{\mathfrak{P}}$
contains a non-trivial congruence subgroup of
![]() $\operatorname{Sp}_{4}({\mathcal{O}}_{E})$
. In particular,
$\operatorname{Sp}_{4}({\mathcal{O}}_{E})$
. In particular,
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{\mathfrak{P}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P})$
is non-trivial for every root
$\operatorname{Im}\unicode[STIX]{x1D70C}_{\mathfrak{P}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P})$
is non-trivial for every root
![]() $\unicode[STIX]{x1D6FC}$
. Now we apply Proposition 6.1 to
$\unicode[STIX]{x1D6FC}$
. Now we apply Proposition 6.1 to
![]() $\mathbf{G}=\operatorname{GSp}_{4}$
,
$\mathbf{G}=\operatorname{GSp}_{4}$
,
![]() $T=T_{2}$
,
$T=T_{2}$
,
![]() $B=B_{2}$
$B=B_{2}$
![]() $A=\mathbb{I}_{\operatorname{Tr}}^{\circ }$
,
$A=\mathbb{I}_{\operatorname{Tr}}^{\circ }$
,
![]() $G=\operatorname{Im}\unicode[STIX]{x1D70C}$
and
$G=\operatorname{Im}\unicode[STIX]{x1D70C}$
and
![]() $Q=\mathfrak{P}$
. We obtain that the projection
$Q=\mathfrak{P}$
. We obtain that the projection
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}\,\cap \,U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })\rightarrow \operatorname{Im}\unicode[STIX]{x1D70C}_{\mathfrak{P}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P})$
is surjective for every
$\operatorname{Im}\unicode[STIX]{x1D70C}\,\cap \,U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })\rightarrow \operatorname{Im}\unicode[STIX]{x1D70C}_{\mathfrak{P}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{P})$
is surjective for every
![]() $\unicode[STIX]{x1D6FC}$
. In particular,
$\unicode[STIX]{x1D6FC}$
. In particular,
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
must be non-trivial for every
$\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
must be non-trivial for every
![]() $\unicode[STIX]{x1D6FC}$
.◻
$\unicode[STIX]{x1D6FC}$
.◻
6.2 A representation with image fixed by the conjugate self-twists
Let
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a finite slope family with associated representation
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a finite slope family with associated representation
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. As before, we assume
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. As before, we assume
![]() $\unicode[STIX]{x1D70C}$
is residually irreducible and
$\unicode[STIX]{x1D70C}$
is residually irreducible and
![]() $\mathbb{Z}_{p}$
-regular. Let
$\mathbb{Z}_{p}$
-regular. Let
![]() $\unicode[STIX]{x1D6E4}$
be the group of conjugate self-twist of
$\unicode[STIX]{x1D6E4}$
be the group of conjugate self-twist of
![]() $\unicode[STIX]{x1D70C}$
and let
$\unicode[STIX]{x1D70C}$
and let
![]() $\mathbb{I}_{0}^{\circ }$
be the subring of
$\mathbb{I}_{0}^{\circ }$
be the subring of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
consisting of the elements fixed by
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
consisting of the elements fixed by
![]() $\unicode[STIX]{x1D6E4}$
. By restricting the domain of
$\unicode[STIX]{x1D6E4}$
. By restricting the domain of
![]() $\unicode[STIX]{x1D70C}$
and replacing it with a suitable conjugate representation, we obtain a
$\unicode[STIX]{x1D70C}$
and replacing it with a suitable conjugate representation, we obtain a
![]() $\mathbb{Z}_{p}$
-regular representation with coefficients in
$\mathbb{Z}_{p}$
-regular representation with coefficients in
![]() $\mathbb{I}_{0}^{\circ }$
. This is the content of the next proposition.
$\mathbb{I}_{0}^{\circ }$
. This is the content of the next proposition.
We write
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
for the finite-order Galois character associated with
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
for the finite-order Galois character associated with
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
. Let
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
. Let
![]() $H_{0}=\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}}\ker \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
. As
$H_{0}=\bigcap _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}}\ker \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
. As
![]() $\unicode[STIX]{x1D6E4}$
is finite
$\unicode[STIX]{x1D6E4}$
is finite
![]() $H_{0}$
is open and normal in
$H_{0}$
is open and normal in
![]() $G_{\mathbb{Q}}$
. Note that
$G_{\mathbb{Q}}$
. Note that
![]() $\operatorname{Tr}(\unicode[STIX]{x1D70C}(H_{0}))\subset \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
. If
$\operatorname{Tr}(\unicode[STIX]{x1D70C}(H_{0}))\subset \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
. If
![]() $\overline{\unicode[STIX]{x1D70C}}|_{H_{0}}$
is irreducible, then by Carayol’s theorem [Reference CarayolCar94, Théorème 1] there exists
$\overline{\unicode[STIX]{x1D70C}}|_{H_{0}}$
is irreducible, then by Carayol’s theorem [Reference CarayolCar94, Théorème 1] there exists
![]() $g\in \operatorname{GL}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
such that the representation
$g\in \operatorname{GL}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
such that the representation
![]() $\unicode[STIX]{x1D70C}^{g}=g\unicode[STIX]{x1D70C}g^{-1}$
satisfies
$\unicode[STIX]{x1D70C}^{g}=g\unicode[STIX]{x1D70C}g^{-1}$
satisfies
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}^{g}|_{H_{0}}\subset \operatorname{GL}_{4}(\mathbb{I}_{0}^{\circ })$
. The hypothesis of irreducibility of
$\operatorname{Im}\unicode[STIX]{x1D70C}^{g}|_{H_{0}}\subset \operatorname{GL}_{4}(\mathbb{I}_{0}^{\circ })$
. The hypothesis of irreducibility of
![]() $\overline{\unicode[STIX]{x1D70C}}|_{H_{0}}$
can probably be checked in the residually full or symmetric cube cases, but it would be too restrictive if we wanted to generalize our work to other interesting cases (for instance, to lifts from
$\overline{\unicode[STIX]{x1D70C}}|_{H_{0}}$
can probably be checked in the residually full or symmetric cube cases, but it would be too restrictive if we wanted to generalize our work to other interesting cases (for instance, to lifts from
![]() $\operatorname{GL}_{2/F}$
with
$\operatorname{GL}_{2/F}$
with
![]() $F/\mathbb{Q}$
real quadratic or from
$F/\mathbb{Q}$
real quadratic or from
![]() $\operatorname{GL}_{1/F}$
with
$\operatorname{GL}_{1/F}$
with
![]() $F/\mathbb{Q}$
CM of degree
$F/\mathbb{Q}$
CM of degree
![]() $4$
). For this reason we do not make the above assumption and we follow instead the approach of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Proposition 4.14], that comes in part from the proof of [Reference LangLan16, Theorem 7.5].
$4$
). For this reason we do not make the above assumption and we follow instead the approach of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Proposition 4.14], that comes in part from the proof of [Reference LangLan16, Theorem 7.5].
Proposition 6.3. There exists an element
![]() $g\in \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
such that:
$g\in \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
such that:
(i)
 $g\unicode[STIX]{x1D70C}g^{-1}(H_{0})\subset \operatorname{GSp}_{4}(\mathbb{I}_{0})$
;
$g\unicode[STIX]{x1D70C}g^{-1}(H_{0})\subset \operatorname{GSp}_{4}(\mathbb{I}_{0})$
;(ii)
 $g\unicode[STIX]{x1D70C}g^{-1}(H_{0})$
contains a diagonal
$g\unicode[STIX]{x1D70C}g^{-1}(H_{0})$
contains a diagonal
 $\mathbb{Z}_{p}$
-regular element.
$\mathbb{Z}_{p}$
-regular element.
Proof. Let
![]() $V$
be a free, rank-four
$V$
be a free, rank-four
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-module. The choice of a basis of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-module. The choice of a basis of
![]() $V$
determines an isomorphism
$V$
determines an isomorphism
![]() $\operatorname{GL}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })\cong \operatorname{Aut}(V)$
, hence an action of
$\operatorname{GL}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })\cong \operatorname{Aut}(V)$
, hence an action of
![]() $\unicode[STIX]{x1D70C}$
on
$\unicode[STIX]{x1D70C}$
on
![]() $V$
. Let
$V$
. Let
![]() $d$
be a
$d$
be a
![]() $\mathbb{Z}_{p}$
-regular element contained in
$\mathbb{Z}_{p}$
-regular element contained in
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}$
. We denote by
$\operatorname{Im}\unicode[STIX]{x1D70C}$
. We denote by
![]() $\{e_{i}\}\text{}_{i=1,\ldots ,4}$
a symplectic basis of
$\{e_{i}\}\text{}_{i=1,\ldots ,4}$
a symplectic basis of
![]() $V$
such that
$V$
such that
![]() $d$
is diagonal. Until further notice, we work in this basis.
$d$
is diagonal. Until further notice, we work in this basis.
By definition of conjugate self-twist, for each
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
there is an equivalence
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
there is an equivalence
![]() $\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}\cong \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}\otimes \unicode[STIX]{x1D70C}$
. This means that there exists a matrix
$\unicode[STIX]{x1D70C}^{\unicode[STIX]{x1D70E}}\cong \unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}\otimes \unicode[STIX]{x1D70C}$
. This means that there exists a matrix
![]() $C_{\unicode[STIX]{x1D70E}}\in \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
such that
$C_{\unicode[STIX]{x1D70E}}\in \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
such that
Recall that we write
![]() $\mathfrak{m}_{\mathbb{I}_{\operatorname{Tr}}^{\circ }}$
for the maximal ideal of
$\mathfrak{m}_{\mathbb{I}_{\operatorname{Tr}}^{\circ }}$
for the maximal ideal of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
and
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
and
![]() $\mathbb{F}$
for the residue field of
$\mathbb{F}$
for the residue field of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
. Let
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
. Let
![]() $\overline{C}_{\unicode[STIX]{x1D70E}}$
be the image of
$\overline{C}_{\unicode[STIX]{x1D70E}}$
be the image of
![]() $C_{\unicode[STIX]{x1D70E}}$
under the natural projection
$C_{\unicode[STIX]{x1D70E}}$
under the natural projection
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })\rightarrow \operatorname{GSp}_{4}(\mathbb{F})$
. We prove the following lemma.
$\operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })\rightarrow \operatorname{GSp}_{4}(\mathbb{F})$
. We prove the following lemma.
Lemma 6.4. For every
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
the matrix
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
the matrix
![]() $C_{\unicode[STIX]{x1D70E}}$
is diagonal and the matrix
$C_{\unicode[STIX]{x1D70E}}$
is diagonal and the matrix
![]() $\overline{C_{\unicode[STIX]{x1D70E}}}$
is scalar.
$\overline{C_{\unicode[STIX]{x1D70E}}}$
is scalar.
Proof. Let
![]() $\unicode[STIX]{x1D6FC}$
be any root of
$\unicode[STIX]{x1D6FC}$
be any root of
![]() $\operatorname{GSp}_{4}$
and
$\operatorname{GSp}_{4}$
and
![]() $u^{\unicode[STIX]{x1D6FC}}$
be a non-trivial element of
$u^{\unicode[STIX]{x1D6FC}}$
be a non-trivial element of
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. Such a
$\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. Such a
![]() $u^{\unicode[STIX]{x1D6FC}}$
exists thanks to Corollary 6.2. Let
$u^{\unicode[STIX]{x1D6FC}}$
exists thanks to Corollary 6.2. Let
![]() $g^{\unicode[STIX]{x1D6FC}}$
be an element of
$g^{\unicode[STIX]{x1D6FC}}$
be an element of
![]() $G_{\mathbb{Q}}$
such that
$G_{\mathbb{Q}}$
such that
![]() $\unicode[STIX]{x1D70C}(g^{\unicode[STIX]{x1D6FC}})=u^{\unicode[STIX]{x1D6FC}}$
. By evaluating (13) at
$\unicode[STIX]{x1D70C}(g^{\unicode[STIX]{x1D6FC}})=u^{\unicode[STIX]{x1D6FC}}$
. By evaluating (13) at
![]() $g^{\unicode[STIX]{x1D6FC}}$
we obtain
$g^{\unicode[STIX]{x1D6FC}}$
we obtain
![]() $C_{\unicode[STIX]{x1D70E}}u^{\unicode[STIX]{x1D6FC}}C_{\unicode[STIX]{x1D70E}}^{-1}=(u^{\unicode[STIX]{x1D6FC}})^{\unicode[STIX]{x1D70E}}$
, which is again an element of
$C_{\unicode[STIX]{x1D70E}}u^{\unicode[STIX]{x1D6FC}}C_{\unicode[STIX]{x1D70E}}^{-1}=(u^{\unicode[STIX]{x1D6FC}})^{\unicode[STIX]{x1D70E}}$
, which is again an element of
![]() $U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. We deduce that
$U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
. We deduce that
![]() $C_{\unicode[STIX]{x1D70E}}$
normalizes
$C_{\unicode[STIX]{x1D70E}}$
normalizes
![]() $U^{\unicode[STIX]{x1D6FC}}(Q(\mathbb{I}_{\operatorname{Tr}}^{\circ }))$
. This holds for every root
$U^{\unicode[STIX]{x1D6FC}}(Q(\mathbb{I}_{\operatorname{Tr}}^{\circ }))$
. This holds for every root
![]() $\unicode[STIX]{x1D6FC}$
, so
$\unicode[STIX]{x1D6FC}$
, so
![]() $C_{\unicode[STIX]{x1D70E}}$
normalizes the Borel subgroups of upper and lower triangular matrices in
$C_{\unicode[STIX]{x1D70E}}$
normalizes the Borel subgroups of upper and lower triangular matrices in
![]() $\operatorname{GSp}_{4}(Q(\mathbb{I}_{\operatorname{Tr}}^{\circ }))$
. As a Borel subgroup is its own normalizer, we conclude that
$\operatorname{GSp}_{4}(Q(\mathbb{I}_{\operatorname{Tr}}^{\circ }))$
. As a Borel subgroup is its own normalizer, we conclude that
![]() $C_{\unicode[STIX]{x1D70E}}$
is diagonal.
$C_{\unicode[STIX]{x1D70E}}$
is diagonal.
By Proposition 5.6(i) the action of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
induces the trivial action of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
induces the trivial action of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\mathbb{F}$
. By evaluating (13) at
$\mathbb{F}$
. By evaluating (13) at
![]() $g^{\unicode[STIX]{x1D6FC}}$
and modulo
$g^{\unicode[STIX]{x1D6FC}}$
and modulo
![]() $\mathfrak{m}_{\mathbb{I}_{\operatorname{Tr}}^{\circ }}$
, we obtain, with the obvious notation,
$\mathfrak{m}_{\mathbb{I}_{\operatorname{Tr}}^{\circ }}$
, we obtain, with the obvious notation,
![]() $\overline{C}_{\unicode[STIX]{x1D70E}}\overline{u}^{\unicode[STIX]{x1D6FC}}(\overline{C}_{\unicode[STIX]{x1D70E}})^{-1}=(\overline{u}^{\unicode[STIX]{x1D6FC}})^{\unicode[STIX]{x1D70E}}=\overline{u}^{\unicode[STIX]{x1D6FC}}$
. As
$\overline{C}_{\unicode[STIX]{x1D70E}}\overline{u}^{\unicode[STIX]{x1D6FC}}(\overline{C}_{\unicode[STIX]{x1D70E}})^{-1}=(\overline{u}^{\unicode[STIX]{x1D6FC}})^{\unicode[STIX]{x1D70E}}=\overline{u}^{\unicode[STIX]{x1D6FC}}$
. As
![]() $C_{\unicode[STIX]{x1D70E}}$
is diagonal and
$C_{\unicode[STIX]{x1D70E}}$
is diagonal and
![]() $\overline{u}^{\unicode[STIX]{x1D6FC}}\in U^{\unicode[STIX]{x1D6FC}}(\mathbb{F})$
, the left-hand side is
$\overline{u}^{\unicode[STIX]{x1D6FC}}\in U^{\unicode[STIX]{x1D6FC}}(\mathbb{F})$
, the left-hand side is
![]() $\unicode[STIX]{x1D6FC}(\overline{C}_{\unicode[STIX]{x1D70E}})\overline{u}^{\unicode[STIX]{x1D6FC}}$
. We deduce that
$\unicode[STIX]{x1D6FC}(\overline{C}_{\unicode[STIX]{x1D70E}})\overline{u}^{\unicode[STIX]{x1D6FC}}$
. We deduce that
![]() $\unicode[STIX]{x1D6FC}(\overline{C}_{\unicode[STIX]{x1D70E}})=1$
. As this holds for every root
$\unicode[STIX]{x1D6FC}(\overline{C}_{\unicode[STIX]{x1D70E}})=1$
. As this holds for every root
![]() $\unicode[STIX]{x1D6FC}$
, we conclude that
$\unicode[STIX]{x1D6FC}$
, we conclude that
![]() $\overline{C}_{\unicode[STIX]{x1D70E}}$
is scalar.◻
$\overline{C}_{\unicode[STIX]{x1D70E}}$
is scalar.◻
We write
![]() $C$
for the map
$C$
for the map
![]() $\unicode[STIX]{x1D6E4}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
defined by
$\unicode[STIX]{x1D6E4}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
defined by
![]() $C(\unicode[STIX]{x1D70E})=C_{\unicode[STIX]{x1D70E}}$
. We show that
$C(\unicode[STIX]{x1D70E})=C_{\unicode[STIX]{x1D70E}}$
. We show that
![]() $C$
can be modified into a
$C$
can be modified into a
![]() $1$
-cocycle that still satisfies (13). For every
$1$
-cocycle that still satisfies (13). For every
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
and every
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
and every
![]() $i$
,
$i$
,
![]() $1\leqslant i\leqslant 4$
, let
$1\leqslant i\leqslant 4$
, let
![]() $(C_{\unicode[STIX]{x1D70E}})_{i}$
denote the scalar matrix whose entries coincide with
$(C_{\unicode[STIX]{x1D70E}})_{i}$
denote the scalar matrix whose entries coincide with
![]() $i$
th diagonal entry of
$i$
th diagonal entry of
![]() $C_{\unicode[STIX]{x1D70E}}$
. Define a map
$C_{\unicode[STIX]{x1D70E}}$
. Define a map
![]() $C_{i}^{\prime }:\unicode[STIX]{x1D6E4}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
by
$C_{i}^{\prime }:\unicode[STIX]{x1D6E4}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
by
![]() $C_{i}^{\prime }(\unicode[STIX]{x1D70E})=(C_{\unicode[STIX]{x1D70E}})_{i}^{-1}C_{\unicode[STIX]{x1D70E}}$
. A simple check using (13) and the cocycle identity for the elements
$C_{i}^{\prime }(\unicode[STIX]{x1D70E})=(C_{\unicode[STIX]{x1D70E}})_{i}^{-1}C_{\unicode[STIX]{x1D70E}}$
. A simple check using (13) and the cocycle identity for the elements
![]() $\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
(Proposition 5.2(iii)) shows that
$\unicode[STIX]{x1D702}_{\unicode[STIX]{x1D70E}}$
(Proposition 5.2(iii)) shows that
![]() $C_{i}^{\prime }$
is a
$C_{i}^{\prime }$
is a
![]() $1$
-cocycle.
$1$
-cocycle.
Set
![]() $C_{\unicode[STIX]{x1D70E}}^{\prime }=C_{i}^{\prime }(\unicode[STIX]{x1D70E})$
. We have
$C_{\unicode[STIX]{x1D70E}}^{\prime }=C_{i}^{\prime }(\unicode[STIX]{x1D70E})$
. We have
By Lemma 6.4
![]() $\overline{C}_{\unicode[STIX]{x1D70E}}$
is scalar, so we obtain
$\overline{C}_{\unicode[STIX]{x1D70E}}$
is scalar, so we obtain
![]() $\overline{C_{\unicode[STIX]{x1D70E}}^{\prime }}=(\overline{C}_{\unicode[STIX]{x1D70E}})_{i}^{-1}\overline{C}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D7D9}_{4}$
with the obvious notation.
$\overline{C_{\unicode[STIX]{x1D70E}}^{\prime }}=(\overline{C}_{\unicode[STIX]{x1D70E}})_{i}^{-1}\overline{C}_{\unicode[STIX]{x1D70E}}=\unicode[STIX]{x1D7D9}_{4}$
with the obvious notation.
Recall that
![]() $\{e_{i}\}\text{}_{i=1,\ldots ,4}$
is our chosen basis of the free
$\{e_{i}\}\text{}_{i=1,\ldots ,4}$
is our chosen basis of the free
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-module
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-module
![]() $V$
, on which
$V$
, on which
![]() $G_{\mathbb{Q}}$
acts via
$G_{\mathbb{Q}}$
acts via
![]() $\unicode[STIX]{x1D70C}$
. For every
$\unicode[STIX]{x1D70C}$
. For every
![]() $v\in V$
, we write as
$v\in V$
, we write as
![]() $v=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}(v)e_{i}$
its unique decomposition in the basis
$v=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}(v)e_{i}$
its unique decomposition in the basis
![]() $(e_{i})_{i=1,\ldots ,4}$
, with
$(e_{i})_{i=1,\ldots ,4}$
, with
![]() $\unicode[STIX]{x1D706}_{i}(v)\in \mathbb{I}_{\operatorname{Tr}}^{\circ }$
for
$\unicode[STIX]{x1D706}_{i}(v)\in \mathbb{I}_{\operatorname{Tr}}^{\circ }$
for
![]() $1\leqslant i\leqslant 4$
. For every
$1\leqslant i\leqslant 4$
. For every
![]() $v\in V$
and every
$v\in V$
and every
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
, we set
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
, we set
![]() $v^{[\unicode[STIX]{x1D70E}]}=(C_{\unicode[STIX]{x1D70E}}^{\prime })^{-1}\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}(v)^{\unicode[STIX]{x1D70E}}e_{i}$
. This defines an action of
$v^{[\unicode[STIX]{x1D70E}]}=(C_{\unicode[STIX]{x1D70E}}^{\prime })^{-1}\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}(v)^{\unicode[STIX]{x1D70E}}e_{i}$
. This defines an action of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $V$
because
$V$
because
![]() $C_{\unicode[STIX]{x1D70E}}^{\prime }$
is a
$C_{\unicode[STIX]{x1D70E}}^{\prime }$
is a
![]() $1$
-cocycle. Let
$1$
-cocycle. Let
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
denote the set of elements of
$V^{[\unicode[STIX]{x1D6E4}]}$
denote the set of elements of
![]() $V$
fixed by
$V$
fixed by
![]() $\unicode[STIX]{x1D6E4}$
. The action of
$\unicode[STIX]{x1D6E4}$
. The action of
![]() $\unicode[STIX]{x1D6E4}$
is clearly
$\unicode[STIX]{x1D6E4}$
is clearly
![]() $\mathbb{I}_{0}^{\circ }$
-linear, so
$\mathbb{I}_{0}^{\circ }$
-linear, so
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
has a structure of
$V^{[\unicode[STIX]{x1D6E4}]}$
has a structure of
![]() $\mathbb{I}_{0}^{\circ }$
-submodule of
$\mathbb{I}_{0}^{\circ }$
-submodule of
![]() $V$
.
$V$
.
Let
![]() $v\in V^{[\unicode[STIX]{x1D6E4}]}$
and
$v\in V^{[\unicode[STIX]{x1D6E4}]}$
and
![]() $h\in H_{0}$
. Then
$h\in H_{0}$
. Then
![]() $\unicode[STIX]{x1D70C}(h)v$
is also in
$\unicode[STIX]{x1D70C}(h)v$
is also in
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
, as we see by a direct calculation using (14). We deduce that the action of
$V^{[\unicode[STIX]{x1D6E4}]}$
, as we see by a direct calculation using (14). We deduce that the action of
![]() $G_{\mathbb{Q}}$
on
$G_{\mathbb{Q}}$
on
![]() $V$
via
$V$
via
![]() $\unicode[STIX]{x1D70C}$
induces an action of
$\unicode[STIX]{x1D70C}$
induces an action of
![]() $H_{0}$
on
$H_{0}$
on
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
. We will conclude the proof of the proposition after having studied the structure of
$V^{[\unicode[STIX]{x1D6E4}]}$
. We will conclude the proof of the proposition after having studied the structure of
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
.
$V^{[\unicode[STIX]{x1D6E4}]}$
.
Lemma 6.5. The
![]() $\mathbb{I}_{0}^{\circ }$
-submodule
$\mathbb{I}_{0}^{\circ }$
-submodule
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
of
$V^{[\unicode[STIX]{x1D6E4}]}$
of
![]() $V$
is free of rank four and its
$V$
is free of rank four and its
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-span is
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-span is
![]() $V$
.
$V$
.
Proof. Choose
![]() $i\in \{1,\ldots ,4\}$
. We construct a non-zero,
$i\in \{1,\ldots ,4\}$
. We construct a non-zero,
![]() $\unicode[STIX]{x1D6E4}$
-invariant element
$\unicode[STIX]{x1D6E4}$
-invariant element
![]() $w_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
. The submodule
$w_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
. The submodule
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
is stable under
$\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
is stable under
![]() $\unicode[STIX]{x1D6E4}$
because
$\unicode[STIX]{x1D6E4}$
because
![]() $C_{\unicode[STIX]{x1D70E}}^{\prime }$
is diagonal. The action of
$C_{\unicode[STIX]{x1D70E}}^{\prime }$
is diagonal. The action of
![]() $\unicode[STIX]{x1D6E4}$
on
$\unicode[STIX]{x1D6E4}$
on
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
induces an action of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
induces an action of
![]() $\unicode[STIX]{x1D6E4}$
on the one-dimensional
$\unicode[STIX]{x1D6E4}$
on the one-dimensional
![]() $\mathbb{F}$
-vector space
$\mathbb{F}$
-vector space
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\otimes _{\mathbb{I}_{\operatorname{Tr}}^{\circ }}\mathbb{F}$
. Recall that the conjugate self-twists induce the identity on
$\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\otimes _{\mathbb{I}_{\operatorname{Tr}}^{\circ }}\mathbb{F}$
. Recall that the conjugate self-twists induce the identity on
![]() $\mathbb{F}$
by Proposition 5.6(i) and that the matrix
$\mathbb{F}$
by Proposition 5.6(i) and that the matrix
![]() $\overline{C_{\unicode[STIX]{x1D70E}}^{\prime }}$
is trivial for every
$\overline{C_{\unicode[STIX]{x1D70E}}^{\prime }}$
is trivial for every
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
, so
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
, so
![]() $\unicode[STIX]{x1D6E4}$
acts trivially on
$\unicode[STIX]{x1D6E4}$
acts trivially on
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\otimes _{\mathbb{I}_{\operatorname{Tr}}^{\circ }}\mathbb{F}$
.
$\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\otimes _{\mathbb{I}_{\operatorname{Tr}}^{\circ }}\mathbb{F}$
.
For
![]() $x\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
, we let
$x\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
, we let
![]() $\overline{x}$
be the image of
$\overline{x}$
be the image of
![]() $x$
via the natural projection
$x$
via the natural projection
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\otimes _{\mathbb{I}_{\operatorname{Tr}}^{\circ }}\mathbb{F}$
. Choose any
$\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\rightarrow \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\otimes _{\mathbb{I}_{\operatorname{Tr}}^{\circ }}\mathbb{F}$
. Choose any
![]() $v_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
such that
$v_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
such that
![]() $\overline{v}_{i}\neq 0$
. Let
$\overline{v}_{i}\neq 0$
. Let
![]() $w_{i}=\sum _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}}v_{i}^{[\unicode[STIX]{x1D70E}]}$
. Clearly
$w_{i}=\sum _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}}v_{i}^{[\unicode[STIX]{x1D70E}]}$
. Clearly
![]() $w_{i}$
is invariant under the action of
$w_{i}$
is invariant under the action of
![]() $\unicode[STIX]{x1D6E4}$
. We show that
$\unicode[STIX]{x1D6E4}$
. We show that
![]() $w_{i}\neq 0$
. Then
$w_{i}\neq 0$
. Then
![]() $\overline{w}_{i}=\sum _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}}\overline{v}_{i}^{[\unicode[STIX]{x1D70E}]}=\sum _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}}\overline{v}_{i}=\operatorname{card}(\unicode[STIX]{x1D6E4})\cdot \overline{v}_{i}$
because
$\overline{w}_{i}=\sum _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}}\overline{v}_{i}^{[\unicode[STIX]{x1D70E}]}=\sum _{\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}}\overline{v}_{i}=\operatorname{card}(\unicode[STIX]{x1D6E4})\cdot \overline{v}_{i}$
because
![]() $\unicode[STIX]{x1D6E4}$
acts trivially on
$\unicode[STIX]{x1D6E4}$
acts trivially on
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\otimes _{\mathbb{I}_{\operatorname{Tr}}^{\circ }}\mathbb{F}$
. By Remark 5.3, the only possible prime factors of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}\otimes _{\mathbb{I}_{\operatorname{Tr}}^{\circ }}\mathbb{F}$
. By Remark 5.3, the only possible prime factors of
![]() $\operatorname{card}(\unicode[STIX]{x1D6E4})$
are
$\operatorname{card}(\unicode[STIX]{x1D6E4})$
are
![]() $2$
and
$2$
and
![]() $3$
. As we supposed that
$3$
. As we supposed that
![]() $p\geqslant 5$
, we have
$p\geqslant 5$
, we have
![]() $\operatorname{card}(\unicode[STIX]{x1D6E4})\neq 0$
in
$\operatorname{card}(\unicode[STIX]{x1D6E4})\neq 0$
in
![]() $\mathbb{F}$
. We deduce that
$\mathbb{F}$
. We deduce that
![]() $\overline{w}_{i}=\operatorname{card}(\unicode[STIX]{x1D6E4})\overline{v}_{i}\neq 0$
in
$\overline{w}_{i}=\operatorname{card}(\unicode[STIX]{x1D6E4})\overline{v}_{i}\neq 0$
in
![]() $\mathbb{F}$
, so
$\mathbb{F}$
, so
![]() $w_{i}\neq 0$
.
$w_{i}\neq 0$
.
Note that
![]() $\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is an
$\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is an
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-basis of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-basis of
![]() $V$
because
$V$
because
![]() $\overline{w}_{i}\neq 0$
for every
$\overline{w}_{i}\neq 0$
for every
![]() $i$
. In particular, the
$i$
. In particular, the
![]() $\mathbb{I}_{0}^{\circ }$
-span of the set
$\mathbb{I}_{0}^{\circ }$
-span of the set
![]() $\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is a free, rank-four
$\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is a free, rank-four
![]() $\mathbb{I}_{0}^{\circ }$
-submodule of
$\mathbb{I}_{0}^{\circ }$
-submodule of
![]() $V$
. As
$V$
. As
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
has a structure of
$V^{[\unicode[STIX]{x1D6E4}]}$
has a structure of
![]() $\mathbb{I}_{0}^{\circ }$
-module and
$\mathbb{I}_{0}^{\circ }$
-module and
![]() $w_{i}\in V^{[\unicode[STIX]{x1D6E4}]}$
for every
$w_{i}\in V^{[\unicode[STIX]{x1D6E4}]}$
for every
![]() $i$
, there is an inclusion
$i$
, there is an inclusion
![]() $\sum _{i=1}^{4}\mathbb{I}_{0}^{\circ }w_{i}\subset V^{[\unicode[STIX]{x1D6E4}]}$
. We show that this is an equality. Let
$\sum _{i=1}^{4}\mathbb{I}_{0}^{\circ }w_{i}\subset V^{[\unicode[STIX]{x1D6E4}]}$
. We show that this is an equality. Let
![]() $v\in V^{[\unicode[STIX]{x1D6E4}]}$
. Write
$v\in V^{[\unicode[STIX]{x1D6E4}]}$
. Write
![]() $v=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}w_{i}$
for some
$v=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}w_{i}$
for some
![]() $\unicode[STIX]{x1D706}_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. Then, for every
$\unicode[STIX]{x1D706}_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. Then, for every
![]() $\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
, we have
$\unicode[STIX]{x1D70E}\in \unicode[STIX]{x1D6E4}$
, we have
![]() $v=v^{[\unicode[STIX]{x1D70E}]}=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D70E}}w_{i}^{[\unicode[STIX]{x1D70E}]}=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D70E}}w_{i}$
. As
$v=v^{[\unicode[STIX]{x1D70E}]}=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D70E}}w_{i}^{[\unicode[STIX]{x1D70E}]}=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D70E}}w_{i}$
. As
![]() $\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is an
$\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is an
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-basis of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-basis of
![]() $V$
, we must have
$V$
, we must have
![]() $\unicode[STIX]{x1D706}_{i}=\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D70E}}$
for every
$\unicode[STIX]{x1D706}_{i}=\unicode[STIX]{x1D706}_{i}^{\unicode[STIX]{x1D70E}}$
for every
![]() $i$
. This holds for every
$i$
. This holds for every
![]() $\unicode[STIX]{x1D70E}$
, so we obtain
$\unicode[STIX]{x1D70E}$
, so we obtain
![]() $\unicode[STIX]{x1D706}_{i}\in \mathbb{I}_{0}^{\circ }$
for every
$\unicode[STIX]{x1D706}_{i}\in \mathbb{I}_{0}^{\circ }$
for every
![]() $i$
. Hence,
$i$
. Hence,
![]() $v=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}w_{i}\in \sum _{i=1}^{4}\mathbb{I}_{0}^{\circ }w_{i}$
.
$v=\sum _{i=1}^{4}\unicode[STIX]{x1D706}_{i}w_{i}\in \sum _{i=1}^{4}\mathbb{I}_{0}^{\circ }w_{i}$
.
The second assertion of the lemma follows immediately from the fact that the set
![]() $\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is contained in
$\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is contained in
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
and is an
$V^{[\unicode[STIX]{x1D6E4}]}$
and is an
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-basis of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-basis of
![]() $V$
.◻
$V$
.◻
Now let
![]() $h\in H_{0}$
. Let
$h\in H_{0}$
. Let
![]() $\{w_{i}\}\text{}_{i=1,\ldots ,4}$
be an
$\{w_{i}\}\text{}_{i=1,\ldots ,4}$
be an
![]() $\mathbb{I}_{0}^{\circ }$
-basis of
$\mathbb{I}_{0}^{\circ }$
-basis of
![]() $V^{[\unicode[STIX]{x1D6E4}]}$
satisfying
$V^{[\unicode[STIX]{x1D6E4}]}$
satisfying
![]() $w_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
, such as that provided by the lemma. As
$w_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
, such as that provided by the lemma. As
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }\cdot V^{[\unicode[STIX]{x1D6E4}]}=V$
,
$\mathbb{I}_{\operatorname{Tr}}^{\circ }\cdot V^{[\unicode[STIX]{x1D6E4}]}=V$
,
![]() $\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is also an
$\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is also an
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-basis of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
-basis of
![]() $V$
. Moreover,
$V$
. Moreover,
![]() $\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is a symplectic basis of
$\{w_{i}\}\text{}_{i=1,\ldots ,4}$
is a symplectic basis of
![]() $V$
, because
$V$
, because
![]() $w_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
for every
$w_{i}\in \mathbb{I}_{\operatorname{Tr}}^{\circ }e_{i}$
for every
![]() $i$
and
$i$
and
![]() $\{e_{i}\}$
is a symplectic basis. By construction, the basis
$\{e_{i}\}$
is a symplectic basis. By construction, the basis
![]() $\{w_{i}\}\text{}_{i=1,\ldots ,4}$
has the two properties we desire.◻
$\{w_{i}\}\text{}_{i=1,\ldots ,4}$
has the two properties we desire.◻
From now on we always work with a
![]() $\mathbb{Z}_{p}$
-regular conjugate of
$\mathbb{Z}_{p}$
-regular conjugate of
![]() $\unicode[STIX]{x1D70C}$
satisfying
$\unicode[STIX]{x1D70C}$
satisfying
![]() $\unicode[STIX]{x1D70C}(H_{0})\subset \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
.
$\unicode[STIX]{x1D70C}(H_{0})\subset \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
.
6.3 Lifting unipotent elements
We give a definition and a lemma that will be important in the following. Let
![]() $B{\hookrightarrow}A$
be an integral extension of Noetherian integral domains. We call an
$B{\hookrightarrow}A$
be an integral extension of Noetherian integral domains. We call an
![]() $A$
-lattice in
$A$
-lattice in
![]() $B$
an
$B$
an
![]() $A$
-submodule of
$A$
-submodule of
![]() $B$
generated by the elements of a basis of
$B$
generated by the elements of a basis of
![]() $Q(B)$
over
$Q(B)$
over
![]() $Q(A)$
.
$Q(A)$
.
Lemma 6.6 [Reference LangLan16, Lemma 4.10].
Every
![]() $A$
-lattice in
$A$
-lattice in
![]() $B$
contains a non-zero ideal of
$B$
contains a non-zero ideal of
![]() $B$
. Conversely, every non-zero ideal of
$B$
. Conversely, every non-zero ideal of
![]() $B$
contains an
$B$
contains an
![]() $A$
-lattice in
$A$
-lattice in
![]() $B$
.
$B$
.
Let
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a finite slope family of
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a finite slope family of
![]() $\operatorname{GSp}_{4}$
-eigenforms and let
$\operatorname{GSp}_{4}$
-eigenforms and let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the representation associated with
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the representation associated with
![]() $\unicode[STIX]{x1D703}$
. For every root
$\unicode[STIX]{x1D703}$
. For every root
![]() $\unicode[STIX]{x1D6FC}$
, we identify the unipotent group
$\unicode[STIX]{x1D6FC}$
, we identify the unipotent group
![]() $U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })$
with
$U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })$
with
![]() $\mathbb{I}_{0}^{\circ }$
and
$\mathbb{I}_{0}^{\circ }$
and
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })$
with a
$\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })$
with a
![]() $\mathbb{Z}_{p}$
-submodule of
$\mathbb{Z}_{p}$
-submodule of
![]() $\mathbb{I}_{0}^{\circ }$
. The goal of this section is to show that, for every
$\mathbb{I}_{0}^{\circ }$
. The goal of this section is to show that, for every
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}$
contains a basis of a
$\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}$
contains a basis of a
![]() $\unicode[STIX]{x1D6EC}_{h}$
-lattice in
$\unicode[STIX]{x1D6EC}_{h}$
-lattice in
![]() $\mathbb{I}_{0}^{\circ }$
. Our strategy is similar to that of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, §4.9], which in turn is inspired by [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15] and [Reference LangLan16]. We proceed in two main steps, by showing that:
$\mathbb{I}_{0}^{\circ }$
. Our strategy is similar to that of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, §4.9], which in turn is inspired by [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15] and [Reference LangLan16]. We proceed in two main steps, by showing that:
(i) there exists a non-critical arithmetic prime
 $P_{\text{}\underline{k}}\subset \unicode[STIX]{x1D6EC}_{h}$
such that
$P_{\text{}\underline{k}}\subset \unicode[STIX]{x1D6EC}_{h}$
such that
 $\operatorname{Im}\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
contains a basis of a
$\operatorname{Im}\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
contains a basis of a
 $\unicode[STIX]{x1D6EC}_{h}/P_{\text{}\underline{k}}$
-lattice in
$\unicode[STIX]{x1D6EC}_{h}/P_{\text{}\underline{k}}$
-lattice in
 $\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
;
$\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
;(ii) the natural morphism
 $\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })\rightarrow \operatorname{Im}\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
is surjective, so we can lift a basis as in point (i) to a basis of a
$\operatorname{Im}\unicode[STIX]{x1D70C}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })\rightarrow \operatorname{Im}\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
is surjective, so we can lift a basis as in point (i) to a basis of a
 $\unicode[STIX]{x1D6EC}_{h}$
-lattice in
$\unicode[STIX]{x1D6EC}_{h}$
-lattice in
 $\mathbb{I}_{0}^{\circ }$
.
$\mathbb{I}_{0}^{\circ }$
.
Part (i) is proved via Theorem 3.12 and a result about the lifting of conjugate self-twists from
![]() $\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }}$
to
$\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }}$
to
![]() $\unicode[STIX]{x1D70C}$
(Proposition 5.4). Part (ii) will result from an application of Proposition 6.1.
$\unicode[STIX]{x1D70C}$
(Proposition 5.4). Part (ii) will result from an application of Proposition 6.1.
We start by stating that we can choose an arithmetic prime with special properties. The following lemma follows from a simple Zariski-density argument, relying on the fact that the weights of the symmetric cube lifts are contained in a two-dimensional (that is, one-parameter) subscheme of
![]() $\operatorname{Spec}\unicode[STIX]{x1D6EC}_{h}$
.
$\operatorname{Spec}\unicode[STIX]{x1D6EC}_{h}$
.
Lemma 6.7. Suppose that
![]() $\overline{\unicode[STIX]{x1D70C}}$
is either full or of symmetric cube type. Then there exists an arithmetic prime
$\overline{\unicode[STIX]{x1D70C}}$
is either full or of symmetric cube type. Then there exists an arithmetic prime
![]() $P_{\text{}\underline{k}}$
of
$P_{\text{}\underline{k}}$
of
![]() $\unicode[STIX]{x1D6EC}_{h}$
such that:
$\unicode[STIX]{x1D6EC}_{h}$
such that:
(i)
 $P_{\text{}\underline{k}}$
is non-critical for
$P_{\text{}\underline{k}}$
is non-critical for
 $\mathbb{I}^{\circ }$
in the sense of Definition 4.5;
$\mathbb{I}^{\circ }$
in the sense of Definition 4.5;(ii) for every prime
 $\mathfrak{P}\subset \mathbb{I}^{\circ }$
lying above
$\mathfrak{P}\subset \mathbb{I}^{\circ }$
lying above
 $P_{\text{}\underline{k}}$
, the classical eigenform corresponding to
$P_{\text{}\underline{k}}$
, the classical eigenform corresponding to
 $\mathfrak{P}$
is not the symmetric cube lift of a
$\mathfrak{P}$
is not the symmetric cube lift of a
 $\operatorname{GL}_{2}$
-eigenform.
$\operatorname{GL}_{2}$
-eigenform.
Let
![]() $\mathfrak{m}_{0}$
denote the maximal ideal of
$\mathfrak{m}_{0}$
denote the maximal ideal of
![]() $\mathbb{I}_{0}^{\circ }$
. Let
$\mathbb{I}_{0}^{\circ }$
. Let
![]() $H=\{g\in H_{0}\,|\,\unicode[STIX]{x1D70C}(g)\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{m}_{0})\}$
, that is a normal open subgroup of
$H=\{g\in H_{0}\,|\,\unicode[STIX]{x1D70C}(g)\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}\mathfrak{m}_{0})\}$
, that is a normal open subgroup of
![]() $H_{0}$
. We define a representation
$H_{0}$
. We define a representation
![]() $\unicode[STIX]{x1D70C}_{0}:H\rightarrow \operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ })$
by setting
$\unicode[STIX]{x1D70C}_{0}:H\rightarrow \operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ })$
by setting
Here the square root is defined via the usual power series, that converges on
![]() $\unicode[STIX]{x1D70C}(H)$
. Even though our results are all stated for the representation
$\unicode[STIX]{x1D70C}(H)$
. Even though our results are all stated for the representation
![]() $\unicode[STIX]{x1D70C}$
, in an intermediate step we will need to work with
$\unicode[STIX]{x1D70C}$
, in an intermediate step we will need to work with
![]() $\unicode[STIX]{x1D70C}_{0}$
and its reduction modulo a prime ideal of
$\unicode[STIX]{x1D70C}_{0}$
and its reduction modulo a prime ideal of
![]() $\mathbb{I}_{0}^{\circ }$
. We now show how it will be possible to transfer our results back to
$\mathbb{I}_{0}^{\circ }$
. We now show how it will be possible to transfer our results back to
![]() $\unicode[STIX]{x1D70C}_{0}$
.
$\unicode[STIX]{x1D70C}_{0}$
.
For the rest of this section, we fix an arithmetic prime
![]() $P_{\text{}\underline{k}}$
of
$P_{\text{}\underline{k}}$
of
![]() $\unicode[STIX]{x1D6EC}_{h}$
satisfying conditions (i) and (ii) in Lemma 6.7. By the étaleness condition in Definition 4.5,
$\unicode[STIX]{x1D6EC}_{h}$
satisfying conditions (i) and (ii) in Lemma 6.7. By the étaleness condition in Definition 4.5,
![]() $P_{\text{}\underline{k}}\mathbb{I}^{\circ }$
is an intersection of distinct primes of
$P_{\text{}\underline{k}}\mathbb{I}^{\circ }$
is an intersection of distinct primes of
![]() $\mathbb{I}^{\circ }$
, so
$\mathbb{I}^{\circ }$
, so
![]() $P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
is an intersection of distinct primes of
$P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
is an intersection of distinct primes of
![]() $\mathbb{I}_{0}^{\circ }$
. Let
$\mathbb{I}_{0}^{\circ }$
. Let
![]() $\mathfrak{Q}_{1},\mathfrak{Q}_{2},\ldots ,\mathfrak{Q}_{d}$
be the prime divisors of
$\mathfrak{Q}_{1},\mathfrak{Q}_{2},\ldots ,\mathfrak{Q}_{d}$
be the prime divisors of
![]() $P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
. Let
$P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
. Let
![]() $\mathfrak{I}$
be either
$\mathfrak{I}$
be either
![]() $P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
or
$P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
or
![]() $\mathfrak{Q}_{i}$
for some
$\mathfrak{Q}_{i}$
for some
![]() $i\in \{1,2,\ldots ,d\}$
.
$i\in \{1,2,\ldots ,d\}$
.
Lemma 6.8. The group
![]() $\unicode[STIX]{x1D70C}(H)$
contains a non-trivial congruence subgroup of
$\unicode[STIX]{x1D70C}(H)$
contains a non-trivial congruence subgroup of
![]() $\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{I})$
if and only if the group
$\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{I})$
if and only if the group
![]() $\unicode[STIX]{x1D70C}_{0}(H)$
does.
$\unicode[STIX]{x1D70C}_{0}(H)$
does.
Proof. The lemma is proved in the same way as [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Proposition 4.22], by replacing Tazhetdinov’s result on subnormal subgroups of symplectic groups of genus
![]() $1$
with his result in genus
$1$
with his result in genus
![]() $2$
[Reference TazhetdinovTaz85, Theorem].◻
$2$
[Reference TazhetdinovTaz85, Theorem].◻
The following is a consequence of Proposition 5.15 and Lemma 6.8, together with our choice of
![]() $P_{\text{}\underline{k}}$
.
$P_{\text{}\underline{k}}$
.
Lemma 6.9. Let
![]() $\mathfrak{Q}$
be a prime of
$\mathfrak{Q}$
be a prime of
![]() $\mathbb{I}_{0}^{\circ }$
lying over
$\mathbb{I}_{0}^{\circ }$
lying over
![]() $P_{\text{}\underline{k}}$
. Then the image of
$P_{\text{}\underline{k}}$
. Then the image of
![]() $\unicode[STIX]{x1D70C}_{0,\mathfrak{Q}}$
contains a non-trivial congruence subgroup of
$\unicode[STIX]{x1D70C}_{0,\mathfrak{Q}}$
contains a non-trivial congruence subgroup of
![]() $\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{Q})$
.
$\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{Q})$
.
Proof. By Proposition 5.15, the image of
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{Q}}$
contains a non-trivial congruence subgroup of
$\unicode[STIX]{x1D70C}_{\mathfrak{Q}}$
contains a non-trivial congruence subgroup of
![]() $\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{Q})$
. As
$\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{Q})$
. As
![]() $H$
is a finite index subgroup of
$H$
is a finite index subgroup of
![]() $G_{\mathbb{Q}}$
, the same is true if we replace
$G_{\mathbb{Q}}$
, the same is true if we replace
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{Q}}$
by
$\unicode[STIX]{x1D70C}_{\mathfrak{Q}}$
by
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{Q}}|_{H}$
. Now the conclusion follows from Lemma 6.8 applied to
$\unicode[STIX]{x1D70C}_{\mathfrak{Q}}|_{H}$
. Now the conclusion follows from Lemma 6.8 applied to
![]() $\mathfrak{I}=\mathfrak{Q}$
.◻
$\mathfrak{I}=\mathfrak{Q}$
.◻
6.4 Big image in a product
Lifting the congruence subgroup of Lemma 6.9 to
![]() $\mathbb{I}^{\circ }$
does not provide the information we need on the image of
$\mathbb{I}^{\circ }$
does not provide the information we need on the image of
![]() $\unicode[STIX]{x1D70C}_{0}$
. We need the following fullness result for
$\unicode[STIX]{x1D70C}_{0}$
. We need the following fullness result for
![]() $\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}$
.
$\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}$
.
Proposition 6.10. The image of the representation
![]() $\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}$
contains a non-trivial congruence subgroup of
$\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}$
contains a non-trivial congruence subgroup of
![]() $\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
.
$\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
.
6.5 Unipotent subgroups and fullness
Recall that for a root
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\operatorname{GSp}_{4}$
, we denote by
$\operatorname{GSp}_{4}$
, we denote by
![]() $U^{\unicode[STIX]{x1D6FC}}$
the corresponding one-parameter unipotent subgroup of
$U^{\unicode[STIX]{x1D6FC}}$
the corresponding one-parameter unipotent subgroup of
![]() $\operatorname{GSp}_{4}$
and by
$\operatorname{GSp}_{4}$
and by
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}}$
the corresponding nilpotent subalgebra of
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}}$
the corresponding nilpotent subalgebra of
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(R)$
. For an ideal
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(R)$
. For an ideal
![]() $\mathfrak{a}$
of
$\mathfrak{a}$
of
![]() $R$
, we call ‘congruence subalgebra of level
$R$
, we call ‘congruence subalgebra of level
![]() $\mathfrak{a}$
’ of
$\mathfrak{a}$
’ of
![]() $\mathfrak{s}\mathfrak{p}_{4}(R)$
the Lie algebra
$\mathfrak{s}\mathfrak{p}_{4}(R)$
the Lie algebra
![]() $\mathfrak{a}\cdot \mathfrak{s}\mathfrak{p}_{4}(R)$
. The following lemma admits two versions, for Lie algebras and for groups, that can be proved via a computation with Lie brackets and commutators, respectively.
$\mathfrak{a}\cdot \mathfrak{s}\mathfrak{p}_{4}(R)$
. The following lemma admits two versions, for Lie algebras and for groups, that can be proved via a computation with Lie brackets and commutators, respectively.
Lemma 6.11. Let
![]() $R$
be an integral domain. Let
$R$
be an integral domain. Let
![]() $\mathfrak{G}$
be a Lie subalgebra of
$\mathfrak{G}$
be a Lie subalgebra of
![]() $\mathfrak{s}\mathfrak{p}_{4}(R)$
and let
$\mathfrak{s}\mathfrak{p}_{4}(R)$
and let
![]() $G$
be a subgroup of
$G$
be a subgroup of
![]() $\operatorname{Sp}_{4}(R)$
. The following are equivalent:
$\operatorname{Sp}_{4}(R)$
. The following are equivalent:
(1) the Lie algebra
 $\mathfrak{G}$
contains a congruence Lie subalgebra (the group
$\mathfrak{G}$
contains a congruence Lie subalgebra (the group
 $G$
contains a congruence subgroup, respectively) of level a non-zero ideal
$G$
contains a congruence subgroup, respectively) of level a non-zero ideal
 $\mathfrak{a}$
of
$\mathfrak{a}$
of
 $R$
;
$R$
;(2) for every root
 $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
 $\operatorname{Sp}_{4}$
, the nilpotent Lie algebra
$\operatorname{Sp}_{4}$
, the nilpotent Lie algebra
 $\mathfrak{G}\cap \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(R)$
(the unipotent subgroup
$\mathfrak{G}\cap \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(R)$
(the unipotent subgroup
 $G\cap U^{\unicode[STIX]{x1D6FC}}(R)$
, respectively) contains a non-zero ideal
$G\cap U^{\unicode[STIX]{x1D6FC}}(R)$
, respectively) contains a non-zero ideal
 $\mathfrak{a}_{\unicode[STIX]{x1D6FC}}$
of
$\mathfrak{a}_{\unicode[STIX]{x1D6FC}}$
of
 $R$
via the identification
$R$
via the identification
 $\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(R)\cong R$
(
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(R)\cong R$
(
 $G\cap U^{\unicode[STIX]{x1D6FC}}(R)\cong R$
, respectively).
$G\cap U^{\unicode[STIX]{x1D6FC}}(R)\cong R$
, respectively).
Moreover:
(i) if condition (1) is satisfied for an ideal
 $\mathfrak{a}$
, then condition (2) is satisfied if we choose
$\mathfrak{a}$
, then condition (2) is satisfied if we choose
 $\mathfrak{a}_{\unicode[STIX]{x1D6FC}}=\mathfrak{a}$
for every
$\mathfrak{a}_{\unicode[STIX]{x1D6FC}}=\mathfrak{a}$
for every
 $\unicode[STIX]{x1D6FC}$
;
$\unicode[STIX]{x1D6FC}$
;(ii) if condition (2) is satisfied for a set of ideals
 $\{\mathfrak{a}_{\unicode[STIX]{x1D6FC}}\}\text{}_{\unicode[STIX]{x1D6FC}}$
, then condition (1) is satisfied for the ideal
$\{\mathfrak{a}_{\unicode[STIX]{x1D6FC}}\}\text{}_{\unicode[STIX]{x1D6FC}}$
, then condition (1) is satisfied for the ideal
 $\mathfrak{a}=\prod _{\unicode[STIX]{x1D6FC}}\mathfrak{a}^{\unicode[STIX]{x1D6FC}}$
, where the product is over all roots
$\mathfrak{a}=\prod _{\unicode[STIX]{x1D6FC}}\mathfrak{a}^{\unicode[STIX]{x1D6FC}}$
, where the product is over all roots
 $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
 $\operatorname{Sp}_{4}$
.
$\operatorname{Sp}_{4}$
.
Remark 6.12. In both versions of Lemma 6.11, if there is an ideal
![]() $\mathfrak{a}^{\prime }$
of
$\mathfrak{a}^{\prime }$
of
![]() $R$
such that the choice
$R$
such that the choice
![]() $\mathfrak{a}_{\unicode[STIX]{x1D6FC}}=\mathfrak{a}^{\prime }$
for every
$\mathfrak{a}_{\unicode[STIX]{x1D6FC}}=\mathfrak{a}^{\prime }$
for every
![]() $\unicode[STIX]{x1D6FC}$
satisfies condition (2), then the choice
$\unicode[STIX]{x1D6FC}$
satisfies condition (2), then the choice
![]() $\mathfrak{a}=(\mathfrak{a}^{\prime })^{2}$
satisfies condition (1).
$\mathfrak{a}=(\mathfrak{a}^{\prime })^{2}$
satisfies condition (1).
By applying Proposition 6.10 and Lemma 6.11 to
![]() $R=\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
and
$R=\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
and
![]() $G=\operatorname{Im}\unicode[STIX]{x1D70C}_{0,P_{\text{}\underline{k}}}$
we obtain the following corollary.
$G=\operatorname{Im}\unicode[STIX]{x1D70C}_{0,P_{\text{}\underline{k}}}$
we obtain the following corollary.
Corollary 6.13. For every root
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\operatorname{GSp}_{4}$
the group
$\operatorname{GSp}_{4}$
the group
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
contains the image of an ideal of
$\operatorname{Im}\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
contains the image of an ideal of
![]() $\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
.
$\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
.
6.6 Lifting the congruence subgroup
If
![]() $\unicode[STIX]{x1D6FC}$
is a root of
$\unicode[STIX]{x1D6FC}$
is a root of
![]() $\operatorname{GSp}_{4}$
,
$\operatorname{GSp}_{4}$
,
![]() $G$
is a group,
$G$
is a group,
![]() $R$
is a ring and
$R$
is a ring and
![]() $\unicode[STIX]{x1D70F}:G\rightarrow \operatorname{GSp}_{4}(R)$
is a representation, let
$\unicode[STIX]{x1D70F}:G\rightarrow \operatorname{GSp}_{4}(R)$
is a representation, let
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}(G)\cap U^{\unicode[STIX]{x1D6FC}}(R)$
. We always identify
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70F})=\unicode[STIX]{x1D70F}(G)\cap U^{\unicode[STIX]{x1D6FC}}(R)$
. We always identify
![]() $U^{\unicode[STIX]{x1D6FC}}(R)$
with
$U^{\unicode[STIX]{x1D6FC}}(R)$
with
![]() $R$
, hence
$R$
, hence
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70F})$
with an additive subgroup of
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70F})$
with an additive subgroup of
![]() $R$
.
$R$
.
Recall that
![]() $\unicode[STIX]{x1D70C}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
is the representation associated with a finite slope family
$\unicode[STIX]{x1D70C}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
is the representation associated with a finite slope family
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
and that
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
and that
![]() $\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}$
is the reduction of
$\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}$
is the reduction of
![]() $\unicode[STIX]{x1D70C}$
modulo
$\unicode[STIX]{x1D70C}$
modulo
![]() $P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
. We use Corollary 6.13 together with Proposition 6.1 to obtain a result on the unipotent subgroups of the image of
$P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
. We use Corollary 6.13 together with Proposition 6.1 to obtain a result on the unipotent subgroups of the image of
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
Proposition 6.14. For every root
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\operatorname{GSp}_{4}$
, the group
$\operatorname{GSp}_{4}$
, the group
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C})$
contains a basis of a
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C})$
contains a basis of a
![]() $\unicode[STIX]{x1D6EC}_{h}$
-lattice in
$\unicode[STIX]{x1D6EC}_{h}$
-lattice in
![]() $\mathbb{I}_{0}^{\circ }$
.
$\mathbb{I}_{0}^{\circ }$
.
Proof. Let
![]() $\unicode[STIX]{x1D70B}_{\text{}\underline{k}}:\mathbb{I}_{0}^{\circ }\rightarrow \mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
be the natural projection. We denote also by
$\unicode[STIX]{x1D70B}_{\text{}\underline{k}}:\mathbb{I}_{0}^{\circ }\rightarrow \mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
be the natural projection. We denote also by
![]() $\unicode[STIX]{x1D70B}_{\text{}\underline{k}}$
the induced map
$\unicode[STIX]{x1D70B}_{\text{}\underline{k}}$
the induced map
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
. For a root
$\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
. For a root
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\operatorname{GSp}_{4}$
, let
$\operatorname{GSp}_{4}$
, let
![]() $\unicode[STIX]{x1D70B}_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}:U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })\rightarrow U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
be the projection induced by
$\unicode[STIX]{x1D70B}_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}:U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })\rightarrow U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
be the projection induced by
![]() $\unicode[STIX]{x1D70B}_{\text{}\underline{k}}$
. Let
$\unicode[STIX]{x1D70B}_{\text{}\underline{k}}$
. Let
![]() $G=\operatorname{Im}\unicode[STIX]{x1D70C}\cap \unicode[STIX]{x1D6E4}_{\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })}(p)$
and
$G=\operatorname{Im}\unicode[STIX]{x1D70C}\cap \unicode[STIX]{x1D6E4}_{\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })}(p)$
and
![]() $G_{P_{\text{}\underline{k}}}=\unicode[STIX]{x1D70B}_{\text{}\underline{k}}(G)$
. The choices
$G_{P_{\text{}\underline{k}}}=\unicode[STIX]{x1D70B}_{\text{}\underline{k}}(G)$
. The choices
![]() $A=\mathbb{I}_{0}^{\circ }$
,
$A=\mathbb{I}_{0}^{\circ }$
,
![]() $\mathbf{G}=\operatorname{GSp}_{4}$
,
$\mathbf{G}=\operatorname{GSp}_{4}$
,
![]() $T=T_{2}$
,
$T=T_{2}$
,
![]() $B=B_{2}$
,
$B=B_{2}$
,
![]() $G=\operatorname{Im}\unicode[STIX]{x1D70C}\cap \unicode[STIX]{x1D6E4}_{\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })}(p)$
and
$G=\operatorname{Im}\unicode[STIX]{x1D70C}\cap \unicode[STIX]{x1D6E4}_{\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })}(p)$
and
![]() $Q=P_{\text{}\underline{k}}$
satisfy the hypotheses of Proposition 6.1, hence
$Q=P_{\text{}\underline{k}}$
satisfy the hypotheses of Proposition 6.1, hence
![]() $\unicode[STIX]{x1D70B}_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}$
induces a surjection
$\unicode[STIX]{x1D70B}_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}$
induces a surjection
![]() $G\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })\rightarrow G_{\text{}\underline{k}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
. Let
$G\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })\rightarrow G_{\text{}\underline{k}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
. Let
![]() $G^{\unicode[STIX]{x1D6FC}}=G\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })$
and
$G^{\unicode[STIX]{x1D6FC}}=G\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })$
and
![]() $G_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}=G_{\text{}\underline{k}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
. As usual, we identify them with
$G_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}=G_{\text{}\underline{k}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
. As usual, we identify them with
![]() $\mathbb{Z}_{p}$
-submodules of
$\mathbb{Z}_{p}$
-submodules of
![]() $\mathbb{I}_{0}^{\circ }$
and
$\mathbb{I}_{0}^{\circ }$
and
![]() $\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
, respectively.
$\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
, respectively.
By Corollary 6.13 there exists a non-zero ideal
![]() $\mathfrak{a}_{\text{}\underline{k}}$
of
$\mathfrak{a}_{\text{}\underline{k}}$
of
![]() $\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
such that
$\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
such that
![]() $\mathfrak{a}_{\text{}\underline{k}}\subset \operatorname{Im}\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
. Set
$\mathfrak{a}_{\text{}\underline{k}}\subset \operatorname{Im}\unicode[STIX]{x1D70C}_{P_{\text{}\underline{k}}}\cap U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ })$
. Set
![]() $\mathfrak{b}_{\text{}\underline{k}}=p\mathfrak{a}_{\text{}\underline{k}}$
. Then
$\mathfrak{b}_{\text{}\underline{k}}=p\mathfrak{a}_{\text{}\underline{k}}$
. Then
![]() $\mathfrak{b}_{\text{}\underline{k}}\subset G_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}$
. By the result of the previous paragraph, the map
$\mathfrak{b}_{\text{}\underline{k}}\subset G_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}$
. By the result of the previous paragraph, the map
![]() $G^{\unicode[STIX]{x1D6FC}}\rightarrow G_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}$
induced by
$G^{\unicode[STIX]{x1D6FC}}\rightarrow G_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}$
induced by
![]() $\unicode[STIX]{x1D70B}_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}$
is surjective, so we can choose a subset
$\unicode[STIX]{x1D70B}_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}$
is surjective, so we can choose a subset
![]() $A$
of
$A$
of
![]() $G^{\unicode[STIX]{x1D6FC}}$
that surjects onto
$G^{\unicode[STIX]{x1D6FC}}$
that surjects onto
![]() $\mathfrak{b}_{\text{}\underline{k}}$
. Let
$\mathfrak{b}_{\text{}\underline{k}}$
. Let
![]() $M$
be the
$M$
be the
![]() $\unicode[STIX]{x1D6EC}_{h}$
-span of
$\unicode[STIX]{x1D6EC}_{h}$
-span of
![]() $A$
in
$A$
in
![]() $\mathbb{I}_{0}^{\circ }$
. Let
$\mathbb{I}_{0}^{\circ }$
. Let
![]() $\mathfrak{b}$
be the pre-image of
$\mathfrak{b}$
be the pre-image of
![]() $\mathfrak{b}_{\text{}\underline{k}}$
via
$\mathfrak{b}_{\text{}\underline{k}}$
via
![]() $\unicode[STIX]{x1D70B}_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}:\mathbb{I}_{0}^{\circ }\rightarrow \mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
. Clearly
$\unicode[STIX]{x1D70B}_{\text{}\underline{k}}^{\unicode[STIX]{x1D6FC}}:\mathbb{I}_{0}^{\circ }\rightarrow \mathbb{I}_{0}^{\circ }/P_{\text{}\underline{k}}\mathbb{I}_{0}^{\circ }$
. Clearly
![]() $A\subset \mathfrak{b}$
, so
$A\subset \mathfrak{b}$
, so
![]() $M$
is a
$M$
is a
![]() $\unicode[STIX]{x1D6EC}_{h}$
-submodule of
$\unicode[STIX]{x1D6EC}_{h}$
-submodule of
![]() $\mathfrak{b}$
. Moreover,
$\mathfrak{b}$
. Moreover,
![]() $M/P_{\text{}\underline{k}}M=\mathfrak{b}_{\text{}\underline{k}}$
by the definition of
$M/P_{\text{}\underline{k}}M=\mathfrak{b}_{\text{}\underline{k}}$
by the definition of
![]() $A$
. As
$A$
. As
![]() $\unicode[STIX]{x1D6EC}$
is local, Nakayama’s lemma implies that the inclusion
$\unicode[STIX]{x1D6EC}$
is local, Nakayama’s lemma implies that the inclusion
![]() $M{\hookrightarrow}\mathfrak{b}$
is an equality. In particular, the
$M{\hookrightarrow}\mathfrak{b}$
is an equality. In particular, the
![]() $\unicode[STIX]{x1D6EC}_{h}$
-span of
$\unicode[STIX]{x1D6EC}_{h}$
-span of
![]() $G^{\unicode[STIX]{x1D6FC}}$
contains an ideal of
$G^{\unicode[STIX]{x1D6FC}}$
contains an ideal of
![]() $\mathbb{I}_{0}^{\circ }$
. By Lemma 6.6, this implies that
$\mathbb{I}_{0}^{\circ }$
. By Lemma 6.6, this implies that
![]() $G^{\unicode[STIX]{x1D6FC}}$
contains a basis of a
$G^{\unicode[STIX]{x1D6FC}}$
contains a basis of a
![]() $\unicode[STIX]{x1D6EC}_{h}$
-lattice in
$\unicode[STIX]{x1D6EC}_{h}$
-lattice in
![]() $\mathbb{I}_{0}^{\circ }$
.◻
$\mathbb{I}_{0}^{\circ }$
.◻
7 Relative Sen theory
Let
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a finite slope family. We keep the notation of the previous sections. Recall that the image of the family in the connected component of unity of the weight space is a disc
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a finite slope family. We keep the notation of the previous sections. Recall that the image of the family in the connected component of unity of the weight space is a disc
![]() $B_{2}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}})$
adapted to the slope
$B_{2}(\unicode[STIX]{x1D705},r_{h,\unicode[STIX]{x1D705}})$
adapted to the slope
![]() $h$
. To guarantee the convergence of a certain exponential series (see §7.4), from now on we make the following assumption:
$h$
. To guarantee the convergence of a certain exponential series (see §7.4), from now on we make the following assumption:
In §4, we defined a family of radii
![]() $\{r_{i}\}\text{}_{i\geqslant 1}$
and we let
$\{r_{i}\}\text{}_{i\geqslant 1}$
and we let
![]() $A_{r_{i}}$
be the ring of rigid analytic functions bounded by
$A_{r_{i}}$
be the ring of rigid analytic functions bounded by
![]() $1$
on
$1$
on
![]() $B_{2}(0,r_{i})$
. For every
$B_{2}(0,r_{i})$
. For every
![]() $i\geqslant 1$
, there is a natural injection
$i\geqslant 1$
, there is a natural injection
![]() $\unicode[STIX]{x1D704}_{r_{i}}:\unicode[STIX]{x1D6EC}_{h}\rightarrow A_{r_{i}}$
. Set
$\unicode[STIX]{x1D704}_{r_{i}}:\unicode[STIX]{x1D6EC}_{h}\rightarrow A_{r_{i}}$
. Set
![]() $\mathbb{I}_{r_{i},0}^{\circ }=\mathbb{I}_{0}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,A_{r_{i}}^{\circ }$
. We endow
$\mathbb{I}_{r_{i},0}^{\circ }=\mathbb{I}_{0}^{\circ }\,\widehat{\otimes }_{\unicode[STIX]{x1D6EC}_{h}}\,A_{r_{i}}^{\circ }$
. We endow
![]() $\mathbb{I}_{r_{i},0}^{\circ }$
with its
$\mathbb{I}_{r_{i},0}^{\circ }$
with its
![]() $p$
-adic topology.
$p$
-adic topology.
Remark 7.1. (i) The ring
![]() $\mathbb{I}_{0}^{\circ }$
admits two inequivalent topologies: the profinite topology and the
$\mathbb{I}_{0}^{\circ }$
admits two inequivalent topologies: the profinite topology and the
![]() $p$
-adic topology. The representation
$p$
-adic topology. The representation
![]() $\unicode[STIX]{x1D70C}$
is continuous with respect to the profinite topology on
$\unicode[STIX]{x1D70C}$
is continuous with respect to the profinite topology on
![]() $\mathbb{I}_{0}^{\circ }$
, but it is not necessarily continuous with respect to the
$\mathbb{I}_{0}^{\circ }$
, but it is not necessarily continuous with respect to the
![]() $p$
-adic topology.
$p$
-adic topology.
(ii) As
![]() $\mathbb{I}_{0}^{\circ }$
is a finite
$\mathbb{I}_{0}^{\circ }$
is a finite
![]() $\unicode[STIX]{x1D6EC}_{h}$
-algebra,
$\unicode[STIX]{x1D6EC}_{h}$
-algebra,
![]() $\mathbb{I}_{r_{i},0}^{\circ }$
is a finite
$\mathbb{I}_{r_{i},0}^{\circ }$
is a finite
![]() $A_{r_{i}}^{\circ }$
-algebra. There is an injective ring morphism
$A_{r_{i}}^{\circ }$
-algebra. There is an injective ring morphism
![]() $\unicode[STIX]{x1D704}_{r_{i}}^{\prime }:\mathbb{I}_{0}^{\circ }{\hookrightarrow}\mathbb{I}_{r_{i},0}^{\circ }$
sending
$\unicode[STIX]{x1D704}_{r_{i}}^{\prime }:\mathbb{I}_{0}^{\circ }{\hookrightarrow}\mathbb{I}_{r_{i},0}^{\circ }$
sending
![]() $f$
to
$f$
to
![]() $f\otimes 1$
. This map is continuous with respect to the profinite topology on
$f\otimes 1$
. This map is continuous with respect to the profinite topology on
![]() $\mathbb{I}_{0}^{\circ }$
and the
$\mathbb{I}_{0}^{\circ }$
and the
![]() $p$
-adic topology on
$p$
-adic topology on
![]() $\mathbb{I}_{r_{i},0}^{\circ }$
: this can be seen by looking at the definition of
$\mathbb{I}_{r_{i},0}^{\circ }$
: this can be seen by looking at the definition of
![]() $A_{r_{i}}^{\circ }$
in §4.1 (for
$A_{r_{i}}^{\circ }$
in §4.1 (for
![]() $g=2$
) and remarking that the
$g=2$
) and remarking that the
![]() $p$
-adic valuation of the variables
$p$
-adic valuation of the variables
![]() $t_{1},t_{2}$
is positive over any disc of radius strictly smaller than
$t_{1},t_{2}$
is positive over any disc of radius strictly smaller than
![]() $1$
.
$1$
.
We associated with
![]() $\unicode[STIX]{x1D703}$
a representation
$\unicode[STIX]{x1D703}$
a representation
![]() $\unicode[STIX]{x1D70C}|_{H_{0}}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
that is continuous with respect to the profinite topologies on both its domain and target. By Remark 7.1(i),
$\unicode[STIX]{x1D70C}|_{H_{0}}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
that is continuous with respect to the profinite topologies on both its domain and target. By Remark 7.1(i),
![]() $\unicode[STIX]{x1D70C}|_{H_{0}}$
needs not be continuous with respect to the
$\unicode[STIX]{x1D70C}|_{H_{0}}$
needs not be continuous with respect to the
![]() $p$
-adic topology on
$p$
-adic topology on
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
. This poses a problem when trying to apply Sen theory. For this reason, we introduce for every
$\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
. This poses a problem when trying to apply Sen theory. For this reason, we introduce for every
![]() $i$
the representation
$i$
the representation
![]() $\unicode[STIX]{x1D70C}_{r_{i}}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r_{i},0}^{\circ })$
defined by
$\unicode[STIX]{x1D70C}_{r_{i}}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r_{i},0}^{\circ })$
defined by
![]() $\unicode[STIX]{x1D70C}_{r_{i}}=\unicode[STIX]{x1D704}_{r_{i}}^{\prime }\circ \,\unicode[STIX]{x1D70C}|_{H_{0}}$
. We deduce from the continuity of
$\unicode[STIX]{x1D70C}_{r_{i}}=\unicode[STIX]{x1D704}_{r_{i}}^{\prime }\circ \,\unicode[STIX]{x1D70C}|_{H_{0}}$
. We deduce from the continuity of
![]() $\unicode[STIX]{x1D704}_{r_{i}}^{\prime }$
that
$\unicode[STIX]{x1D704}_{r_{i}}^{\prime }$
that
![]() $\unicode[STIX]{x1D70C}_{r_{i}}$
is continuous with respect to the profinite topology on
$\unicode[STIX]{x1D70C}_{r_{i}}$
is continuous with respect to the profinite topology on
![]() $H_{0}$
and the
$H_{0}$
and the
![]() $p$
-adic topology on
$p$
-adic topology on
![]() $\mathbb{I}_{r_{i},0}^{\circ }$
. It is clear from the definition that the image of
$\mathbb{I}_{r_{i},0}^{\circ }$
. It is clear from the definition that the image of
![]() $\unicode[STIX]{x1D70C}_{r_{i}}$
is independent of
$\unicode[STIX]{x1D70C}_{r_{i}}$
is independent of
![]() $i$
as a topological group.
$i$
as a topological group.
There is a good notion of Lie algebra for a pro-
![]() $p$
group that is topologically of finite type. For this reason, we further restrict
$p$
group that is topologically of finite type. For this reason, we further restrict
![]() $H_{0}$
so that the image of
$H_{0}$
so that the image of
![]() $\unicode[STIX]{x1D70C}_{r_{i}}$
is a pro-
$\unicode[STIX]{x1D70C}_{r_{i}}$
is a pro-
![]() $p$
group. Let
$p$
group. Let
![]() $H_{r_{1}}=\{g\in H_{0}\,|\,\unicode[STIX]{x1D70C}_{r_{1}}(g)\cong \unicode[STIX]{x1D7D9}_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\}$
and set
$H_{r_{1}}=\{g\in H_{0}\,|\,\unicode[STIX]{x1D70C}_{r_{1}}(g)\cong \unicode[STIX]{x1D7D9}_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\}$
and set
![]() $H_{r_{i}}=H_{r_{1}}$
for every
$H_{r_{i}}=H_{r_{1}}$
for every
![]() $i\geqslant 1$
. The subgroup
$i\geqslant 1$
. The subgroup
![]() $\{M\in \operatorname{GSp}_{4}(\mathbb{I}_{r_{1},0}^{\circ })\,|\,M\cong \unicode[STIX]{x1D7D9}_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\}$
is of finite index in
$\{M\in \operatorname{GSp}_{4}(\mathbb{I}_{r_{1},0}^{\circ })\,|\,M\cong \unicode[STIX]{x1D7D9}_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\}$
is of finite index in
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{r_{1},0}^{\circ })$
. Note that this depends on the fact that we extended the coefficients to
$\operatorname{GSp}_{4}(\mathbb{I}_{r_{1},0}^{\circ })$
. Note that this depends on the fact that we extended the coefficients to
![]() $\mathbb{I}_{r_{1},0}$
, because
$\mathbb{I}_{r_{1},0}$
, because
![]() $\{M\in \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })\,|\,M\cong \unicode[STIX]{x1D7D9}_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\}$
is not of finite index in
$\{M\in \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })\,|\,M\cong \unicode[STIX]{x1D7D9}_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\}$
is not of finite index in
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{0})$
. We deduce that
$\operatorname{GSp}_{4}(\mathbb{I}_{0})$
. We deduce that
![]() $H_{r_{1}}$
is a normal open subgroup of
$H_{r_{1}}$
is a normal open subgroup of
![]() $G_{\mathbb{Q}}$
. Let
$G_{\mathbb{Q}}$
. Let
![]() $K_{H_{r_{i}}}$
be the subfield of
$K_{H_{r_{i}}}$
be the subfield of
![]() $\overline{\mathbb{Q}}$
fixed by
$\overline{\mathbb{Q}}$
fixed by
![]() $H_{r_{i}}$
. It is a finite Galois extension of
$H_{r_{i}}$
. It is a finite Galois extension of
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
Recall that we fixed an embedding
![]() $G_{\mathbb{Q}_{p}}{\hookrightarrow}G_{\mathbb{Q}}$
, identifying
$G_{\mathbb{Q}_{p}}{\hookrightarrow}G_{\mathbb{Q}}$
, identifying
![]() $G_{\mathbb{Q}_{p}}$
with a decomposition subgroup of
$G_{\mathbb{Q}_{p}}$
with a decomposition subgroup of
![]() $G_{\mathbb{Q}}$
at
$G_{\mathbb{Q}}$
at
![]() $p$
. Let
$p$
. Let
![]() $H_{r_{i},p}=H_{r_{i}}\cap G_{\mathbb{Q}_{p}}$
. Let
$H_{r_{i},p}=H_{r_{i}}\cap G_{\mathbb{Q}_{p}}$
. Let
![]() $K_{H_{r_{i}},p}$
be the subfield of
$K_{H_{r_{i}},p}$
be the subfield of
![]() $\overline{\mathbb{Q}}_{p}$
fixed by
$\overline{\mathbb{Q}}_{p}$
fixed by
![]() $H_{r_{i},p}$
. The field
$H_{r_{i},p}$
. The field
![]() $K_{H_{r_{i}},p}$
will play a role when we apply Sen theory. For every
$K_{H_{r_{i}},p}$
will play a role when we apply Sen theory. For every
![]() $i$
, let
$i$
, let
![]() $G_{r_{i}}=\unicode[STIX]{x1D70C}_{r_{i}}(H_{r_{i}})$
and
$G_{r_{i}}=\unicode[STIX]{x1D70C}_{r_{i}}(H_{r_{i}})$
and
![]() $G_{r_{i}}^{\operatorname{loc}}=\unicode[STIX]{x1D70C}_{r_{i}}(H_{r_{i},p})$
.
$G_{r_{i}}^{\operatorname{loc}}=\unicode[STIX]{x1D70C}_{r_{i}}(H_{r_{i},p})$
.
Remark 7.2. The topological Lie groups
![]() $G_{r}$
and
$G_{r}$
and
![]() $G_{r}^{\operatorname{loc}}$
are independent of
$G_{r}^{\operatorname{loc}}$
are independent of
![]() $r$
, in the following sense. For positive integers
$r$
, in the following sense. For positive integers
![]() $i,j$
with
$i,j$
with
![]() $i\leqslant j$
, let
$i\leqslant j$
, let
![]() $\unicode[STIX]{x1D704}_{r_{j}}^{r_{i}}:\mathbb{I}_{r_{j},0}\rightarrow \mathbb{I}_{r_{i},0}$
be the natural morphism induced by the restriction of analytic functions
$\unicode[STIX]{x1D704}_{r_{j}}^{r_{i}}:\mathbb{I}_{r_{j},0}\rightarrow \mathbb{I}_{r_{i},0}$
be the natural morphism induced by the restriction of analytic functions
![]() $A_{r_{j}}\rightarrow A_{r_{i}}$
. As
$A_{r_{j}}\rightarrow A_{r_{i}}$
. As
![]() $H_{r_{i}}=H_{r_{j}}=H_{r_{1}}$
by definition,
$H_{r_{i}}=H_{r_{j}}=H_{r_{1}}$
by definition,
![]() $\unicode[STIX]{x1D704}_{r_{j}}^{r_{i}}$
induces isomorphisms
$\unicode[STIX]{x1D704}_{r_{j}}^{r_{i}}$
induces isomorphisms
![]() $\unicode[STIX]{x1D704}_{r_{j}}^{r_{i}}:G_{r_{j}}\xrightarrow[{}]{{\sim}}G_{r_{i}}$
and
$\unicode[STIX]{x1D704}_{r_{j}}^{r_{i}}:G_{r_{j}}\xrightarrow[{}]{{\sim}}G_{r_{i}}$
and
![]() $\unicode[STIX]{x1D704}_{r_{j}}^{r_{i}}:G_{r_{j}}^{\operatorname{loc}}\xrightarrow[{}]{{\sim}}G_{r_{i}}^{\operatorname{loc}}$
.
$\unicode[STIX]{x1D704}_{r_{j}}^{r_{i}}:G_{r_{j}}^{\operatorname{loc}}\xrightarrow[{}]{{\sim}}G_{r_{i}}^{\operatorname{loc}}$
.
7.1 Big Lie algebras
As before, let
![]() $r$
be a radius among the
$r$
be a radius among the
![]() $r_{i}$
,
$r_{i}$
,
![]() $i\in \mathbb{N}^{{>}0}$
. We will associate with
$i\in \mathbb{N}^{{>}0}$
. We will associate with
![]() $\unicode[STIX]{x1D70C}_{r}(H_{r})$
a Lie algebra that will give the context in which to apply Sen’s results. Our methods require that we work with
$\unicode[STIX]{x1D70C}_{r}(H_{r})$
a Lie algebra that will give the context in which to apply Sen’s results. Our methods require that we work with
![]() $\mathbb{Q}_{p}$
-Lie algebras, so we define the rings
$\mathbb{Q}_{p}$
-Lie algebras, so we define the rings
![]() $A_{r}=A_{r}^{\circ }[p^{-1}]$
and
$A_{r}=A_{r}^{\circ }[p^{-1}]$
and
![]() $\mathbb{I}_{r,0}=\mathbb{I}_{r,0}^{\circ }[p^{-1}]$
.
$\mathbb{I}_{r,0}=\mathbb{I}_{r,0}^{\circ }[p^{-1}]$
.
Let
![]() $\mathfrak{a}$
be a height-two ideal of
$\mathfrak{a}$
be a height-two ideal of
![]() $\mathbb{I}_{r,0}$
. The quotient
$\mathbb{I}_{r,0}$
. The quotient
![]() $\mathbb{I}_{r,0}/\mathfrak{a}$
is a finite-dimensional
$\mathbb{I}_{r,0}/\mathfrak{a}$
is a finite-dimensional
![]() $\mathbb{Q}_{p}$
-algebra. Let
$\mathbb{Q}_{p}$
-algebra. Let
![]() $\unicode[STIX]{x1D70B}_{\mathfrak{a}}:\mathbb{I}_{r,0}\rightarrow \mathbb{I}_{r,0}/\mathfrak{a}$
be the natural projection. We still denote by
$\unicode[STIX]{x1D70B}_{\mathfrak{a}}:\mathbb{I}_{r,0}\rightarrow \mathbb{I}_{r,0}/\mathfrak{a}$
be the natural projection. We still denote by
![]() $\unicode[STIX]{x1D70B}_{\mathfrak{a}}$
the induced map
$\unicode[STIX]{x1D70B}_{\mathfrak{a}}$
the induced map
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{r,0})\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
. Consider the subgroups
$\operatorname{GSp}_{4}(\mathbb{I}_{r,0})\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
. Consider the subgroups
![]() $G_{r,\mathfrak{a}}=\unicode[STIX]{x1D70B}_{\mathfrak{a}}(G_{r})$
and
$G_{r,\mathfrak{a}}=\unicode[STIX]{x1D70B}_{\mathfrak{a}}(G_{r})$
and
![]() $G_{r,\mathfrak{a}}^{\operatorname{loc}}=\unicode[STIX]{x1D70B}_{\mathfrak{a}}(G_{r}^{\operatorname{loc}})$
of
$G_{r,\mathfrak{a}}^{\operatorname{loc}}=\unicode[STIX]{x1D70B}_{\mathfrak{a}}(G_{r}^{\operatorname{loc}})$
of
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
. They are both pro-
$\operatorname{GSp}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
. They are both pro-
![]() $p$
groups and they are topologically of finite type because
$p$
groups and they are topologically of finite type because
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
is. It makes sense to consider the logarithm of an element of
$\operatorname{GSp}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
is. It makes sense to consider the logarithm of an element of
![]() $G_{r,\mathfrak{a}}$
because this group is contained in
$G_{r,\mathfrak{a}}$
because this group is contained in
![]() $\{M\in \operatorname{GSp}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})\,|\,M\cong \unicode[STIX]{x1D7D9}_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\}$
.
$\{M\in \operatorname{GSp}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})\,|\,M\cong \unicode[STIX]{x1D7D9}_{4}\hspace{0.6em}({\rm mod}\hspace{0.2em}p)\}$
.
We attach to
![]() $G_{r,\mathfrak{a}}$
and
$G_{r,\mathfrak{a}}$
and
![]() $G_{r,\mathfrak{a}}^{\operatorname{loc}}$
the
$G_{r,\mathfrak{a}}^{\operatorname{loc}}$
the
![]() $\mathbb{Q}_{p}$
-vector subspaces
$\mathbb{Q}_{p}$
-vector subspaces
![]() $\mathfrak{G}_{r,\mathfrak{a}}$
and
$\mathfrak{G}_{r,\mathfrak{a}}$
and
![]() $\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
of
$\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
of
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
defined by
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
defined by
The
![]() $\mathbb{Q}_{p}$
-Lie algebra structure of
$\mathbb{Q}_{p}$
-Lie algebra structure of
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
restricts to a
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
restricts to a
![]() $\mathbb{Q}_{p}$
-Lie algebra structure on
$\mathbb{Q}_{p}$
-Lie algebra structure on
![]() $\mathfrak{G}_{r,\mathfrak{a}}$
and
$\mathfrak{G}_{r,\mathfrak{a}}$
and
![]() $\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
. These two Lie algebras are finite-dimensional over
$\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
. These two Lie algebras are finite-dimensional over
![]() $\mathbb{Q}_{p}$
because
$\mathbb{Q}_{p}$
because
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
is.
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
is.
Remark 7.3. The Lie algebras
![]() $\mathfrak{G}_{r,\mathfrak{a}}$
and
$\mathfrak{G}_{r,\mathfrak{a}}$
and
![]() $\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
are independent of
$\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
are independent of
![]() $r$
, in a sense analogous to that of Remark 7.2.
$r$
, in a sense analogous to that of Remark 7.2.
Recall that there is a natural injection
![]() $\unicode[STIX]{x1D6EC}_{2}{\hookrightarrow}\unicode[STIX]{x1D6EC}_{h}$
, hence an injection
$\unicode[STIX]{x1D6EC}_{2}{\hookrightarrow}\unicode[STIX]{x1D6EC}_{h}$
, hence an injection
![]() $\unicode[STIX]{x1D6EC}_{2}[p^{-1}]{\hookrightarrow}\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
. For every
$\unicode[STIX]{x1D6EC}_{2}[p^{-1}]{\hookrightarrow}\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
. For every
![]() $\text{}\underline{k}=(k_{1},k_{2})$
, the ideal
$\text{}\underline{k}=(k_{1},k_{2})$
, the ideal
![]() $P_{\text{}\underline{k}}\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
is either prime in
$P_{\text{}\underline{k}}\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
is either prime in
![]() $\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
or equal to
$\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
or equal to
![]() $\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
. We define the set of ‘bad’ ideals
$\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
. We define the set of ‘bad’ ideals
![]() $S_{\unicode[STIX]{x1D6EC}}^{\operatorname{bad}}$
of
$S_{\unicode[STIX]{x1D6EC}}^{\operatorname{bad}}$
of
![]() $\unicode[STIX]{x1D6EC}_{2}[p^{-1}]$
as
$\unicode[STIX]{x1D6EC}_{2}[p^{-1}]$
as
Then we define the set of bad prime ideals of
![]() $\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
as
$\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
as
We will take care to define rings where the images of the ideals in
![]() $S^{\operatorname{bad}}$
consist of invertible elements. The reason for this will be clear in Proposition 7.13. Let
$S^{\operatorname{bad}}$
consist of invertible elements. The reason for this will be clear in Proposition 7.13. Let
![]() $S_{2}$
be the set of ideals
$S_{2}$
be the set of ideals
![]() $\mathfrak{a}$
of
$\mathfrak{a}$
of
![]() $\mathbb{I}_{r,0}$
of height two such that
$\mathbb{I}_{r,0}$
of height two such that
![]() $\mathfrak{a}$
is prime to
$\mathfrak{a}$
is prime to
![]() $P$
for every
$P$
for every
![]() $P\in S^{\operatorname{bad}}$
. Let
$P\in S^{\operatorname{bad}}$
. Let
![]() $S_{2}^{\prime }$
be the subset of prime ideals in
$S_{2}^{\prime }$
be the subset of prime ideals in
![]() $S_{2}$
. We define the ring
$S_{2}$
. We define the ring
where the limit of finite-dimensional
![]() $\mathbb{Q}_{p}$
-Banach spaces is taken with respect to the natural transition maps
$\mathbb{Q}_{p}$
-Banach spaces is taken with respect to the natural transition maps
![]() $\mathbb{I}_{r,0}/\mathfrak{a}_{1}\rightarrow \mathbb{I}_{r,0}/\mathfrak{a}_{2}$
defined for every inclusion of ideals
$\mathbb{I}_{r,0}/\mathfrak{a}_{1}\rightarrow \mathbb{I}_{r,0}/\mathfrak{a}_{2}$
defined for every inclusion of ideals
![]() $\mathfrak{a}_{1}\subset \mathfrak{a}_{2}$
. We equip
$\mathfrak{a}_{1}\subset \mathfrak{a}_{2}$
. We equip
![]() $\mathbb{I}_{r,0}/\mathfrak{a}$
with the
$\mathbb{I}_{r,0}/\mathfrak{a}$
with the
![]() $p$
-adic topology for every
$p$
-adic topology for every
![]() $\mathfrak{a}$
and
$\mathfrak{a}$
and
![]() $\mathbb{B}_{r}$
with the projective limit topology. There is a natural injection
$\mathbb{B}_{r}$
with the projective limit topology. There is a natural injection
![]() $\unicode[STIX]{x1D704}_{\mathbb{B}_{r}}:\mathbb{I}_{r,0}{\hookrightarrow}\mathbb{B}_{r}$
with dense image.
$\unicode[STIX]{x1D704}_{\mathbb{B}_{r}}:\mathbb{I}_{r,0}{\hookrightarrow}\mathbb{B}_{r}$
with dense image.
Now consider the sets
For later use, we define a ring
where the limit of finite-dimensional
![]() $\mathbb{Q}_{p}$
-Banach spaces is taken with respect to the natural transition maps
$\mathbb{Q}_{p}$
-Banach spaces is taken with respect to the natural transition maps
![]() $A_{r}/\mathfrak{a}_{1}\rightarrow A_{r}/\mathfrak{a}_{2}$
defined for every inclusion of ideals
$A_{r}/\mathfrak{a}_{1}\rightarrow A_{r}/\mathfrak{a}_{2}$
defined for every inclusion of ideals
![]() $\mathfrak{a}_{1}\subset \mathfrak{a}_{2}$
. We equip
$\mathfrak{a}_{1}\subset \mathfrak{a}_{2}$
. We equip
![]() $A_{r}/\mathfrak{a}$
with the
$A_{r}/\mathfrak{a}$
with the
![]() $p$
-adic topology for every
$p$
-adic topology for every
![]() $\mathfrak{a}$
and
$\mathfrak{a}$
and
![]() $B_{r}$
with the projective limit topology. There is a natural injection
$B_{r}$
with the projective limit topology. There is a natural injection
![]() $\unicode[STIX]{x1D704}_{B_{r}}:A_{r}{\hookrightarrow}B_{r}$
with dense image. The natural inclusion
$\unicode[STIX]{x1D704}_{B_{r}}:A_{r}{\hookrightarrow}B_{r}$
with dense image. The natural inclusion
![]() $B_{r}{\hookrightarrow}\mathbb{B}_{r}$
gives
$B_{r}{\hookrightarrow}\mathbb{B}_{r}$
gives
![]() $\mathbb{B}_{r}$
a structure of finite
$\mathbb{B}_{r}$
a structure of finite
![]() $B_{r}$
-algebra, as we can deduce from the fact that
$B_{r}$
-algebra, as we can deduce from the fact that
![]() $\mathbb{I}_{r,0}$
is a finite
$\mathbb{I}_{r,0}$
is a finite
![]() $A_{r}$
-algebra.
$A_{r}$
-algebra.
Remark 7.4. For every
![]() $P\in S^{\operatorname{bad}}$
we have
$P\in S^{\operatorname{bad}}$
we have
![]() $P\cdot \mathbb{B}_{r}=\mathbb{B}_{r}$
, because the limit defining
$P\cdot \mathbb{B}_{r}=\mathbb{B}_{r}$
, because the limit defining
![]() $\mathbb{B}_{r}$
is over ideals prime to
$\mathbb{B}_{r}$
is over ideals prime to
![]() $P$
. In the same way, we have
$P$
. In the same way, we have
![]() $P\cdot B_{r}=B_{r}$
for every
$P\cdot B_{r}=B_{r}$
for every
![]() $P\in S_{A}^{\operatorname{bad}}$
.
$P\in S_{A}^{\operatorname{bad}}$
.
We attach to the groups
![]() $G_{r}$
and
$G_{r}$
and
![]() $G_{r}^{\operatorname{loc}}$
two
$G_{r}^{\operatorname{loc}}$
two
![]() $\mathbb{Q}_{p}$
-Lie subalgebras of
$\mathbb{Q}_{p}$
-Lie subalgebras of
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})$
. Let
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})$
. Let
where
![]() $\mathfrak{G}_{r,\mathfrak{a}}$
and
$\mathfrak{G}_{r,\mathfrak{a}}$
and
![]() $\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
are the Lie algebras we attached to
$\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
are the Lie algebras we attached to
![]() $G_{r,\mathfrak{a}}$
and
$G_{r,\mathfrak{a}}$
and
![]() $G_{r,\mathfrak{a}}^{\operatorname{loc}}$
. The
$G_{r,\mathfrak{a}}^{\operatorname{loc}}$
. The
![]() $\mathbb{Q}_{p}$
-Lie algebra structures on
$\mathbb{Q}_{p}$
-Lie algebra structures on
![]() $\mathfrak{G}_{r,\mathfrak{a}}$
and
$\mathfrak{G}_{r,\mathfrak{a}}$
and
![]() $\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
induce
$\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc}}$
induce
![]() $\mathbb{Q}_{p}$
-Lie algebra structures on
$\mathbb{Q}_{p}$
-Lie algebra structures on
![]() $\mathfrak{G}_{r}$
and
$\mathfrak{G}_{r}$
and
![]() $\mathfrak{G}_{r}^{\operatorname{loc}}$
. We endow
$\mathfrak{G}_{r}^{\operatorname{loc}}$
. We endow
![]() $\mathfrak{G}_{r}$
and
$\mathfrak{G}_{r}$
and
![]() $\mathfrak{G}_{r}^{\operatorname{loc}}$
with the
$\mathfrak{G}_{r}^{\operatorname{loc}}$
with the
![]() $p$
-adic topology induced by that on
$p$
-adic topology induced by that on
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})$
.
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})$
.
When we introduce the Sen operators, we will have to extend the scalars of the various rings and Lie algebras to
![]() $\mathbb{C}_{p}$
. We denote this operation by adding a lower index
$\mathbb{C}_{p}$
. We denote this operation by adding a lower index
![]() $\mathbb{C}_{p}$
to the objects previously defined. We still endow all the rings with their
$\mathbb{C}_{p}$
to the objects previously defined. We still endow all the rings with their
![]() $p$
-adic topology. Clearly
$p$
-adic topology. Clearly
![]() $\mathbb{I}_{r,0,\mathbb{C}_{p}}$
has a structure of finite
$\mathbb{I}_{r,0,\mathbb{C}_{p}}$
has a structure of finite
![]() $A_{r,\mathbb{C}_{p}}$
-algebra and
$A_{r,\mathbb{C}_{p}}$
-algebra and
![]() $\mathbb{B}_{r,\mathbb{C}_{p}}$
has a structure of finite
$\mathbb{B}_{r,\mathbb{C}_{p}}$
has a structure of finite
![]() $B_{r,\mathbb{C}_{p}}$
-algebra.
$B_{r,\mathbb{C}_{p}}$
-algebra.
Remark 7.5. The
![]() $\mathbb{Q}_{p}$
-Lie algebras
$\mathbb{Q}_{p}$
-Lie algebras
![]() $\mathfrak{G}_{r}$
and
$\mathfrak{G}_{r}$
and
![]() $\mathfrak{G}_{r}^{\operatorname{loc}}$
do not have a priori any
$\mathfrak{G}_{r}^{\operatorname{loc}}$
do not have a priori any
![]() $\mathbb{B}_{r}$
or
$\mathbb{B}_{r}$
or
![]() $B_{r}$
-module structure. As a crucial step in our arguments we will use Sen theory to induce a
$B_{r}$
-module structure. As a crucial step in our arguments we will use Sen theory to induce a
![]() $B_{r,\mathbb{C}_{p}}$
-vector space (hence a
$B_{r,\mathbb{C}_{p}}$
-vector space (hence a
![]() $B_{r,\mathbb{C}_{p}}$
-Lie algebra) structure on suitable subalgebras of
$B_{r,\mathbb{C}_{p}}$
-Lie algebra) structure on suitable subalgebras of
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}$
.
$\mathfrak{G}_{r,\mathbb{C}_{p}}$
.
7.2 The Sen operator associated with a
 $p$
-adic Galois representation
$p$
-adic Galois representation
Let
![]() $L$
be a
$L$
be a
![]() $p$
-adic field and let
$p$
-adic field and let
![]() ${\mathcal{R}}$
be a Banach
${\mathcal{R}}$
be a Banach
![]() $L$
-algebra. Let
$L$
-algebra. Let
![]() $K$
be another
$K$
be another
![]() $p$
-adic field,
$p$
-adic field,
![]() $m$
be a positive integer and
$m$
be a positive integer and
![]() $\unicode[STIX]{x1D70F}:\operatorname{Gal}(\overline{K}/K)\rightarrow \operatorname{GL}_{m}({\mathcal{R}})$
be a continuous representation. We recall the construction of the Sen operator associated with
$\unicode[STIX]{x1D70F}:\operatorname{Gal}(\overline{K}/K)\rightarrow \operatorname{GL}_{m}({\mathcal{R}})$
be a continuous representation. We recall the construction of the Sen operator associated with
![]() $\unicode[STIX]{x1D70F}$
, following [Reference SenSen93].
$\unicode[STIX]{x1D70F}$
, following [Reference SenSen93].
We fix embeddings of
![]() $K$
and
$K$
and
![]() $L$
in
$L$
in
![]() $\overline{\mathbb{Q}}_{p}$
. The constructions that follow will depend on these choices. We suppose that the Galois closure
$\overline{\mathbb{Q}}_{p}$
. The constructions that follow will depend on these choices. We suppose that the Galois closure
![]() $L^{\operatorname{Gal}}$
of
$L^{\operatorname{Gal}}$
of
![]() $L$
over
$L$
over
![]() $\mathbb{Q}_{p}$
is contained in
$\mathbb{Q}_{p}$
is contained in
![]() $K$
. If this is not the case, we restrict
$K$
. If this is not the case, we restrict
![]() $\unicode[STIX]{x1D70F}$
to the open subgroup
$\unicode[STIX]{x1D70F}$
to the open subgroup
![]() $\operatorname{Gal}(\overline{K}/KL^{\operatorname{Gal}})\subset \operatorname{Gal}(\overline{K}/K)$
. We denote by
$\operatorname{Gal}(\overline{K}/KL^{\operatorname{Gal}})\subset \operatorname{Gal}(\overline{K}/K)$
. We denote by
![]() $\unicode[STIX]{x1D712}:\operatorname{Gal}(\overline{L}/L)\rightarrow \mathbb{Z}_{p}^{\times }$
the
$\unicode[STIX]{x1D712}:\operatorname{Gal}(\overline{L}/L)\rightarrow \mathbb{Z}_{p}^{\times }$
the
![]() $p$
-adic cyclotomic character. Let
$p$
-adic cyclotomic character. Let
![]() $L_{\infty }$
be a totally ramified
$L_{\infty }$
be a totally ramified
![]() $\mathbb{Z}_{p}$
-extension of
$\mathbb{Z}_{p}$
-extension of
![]() $L$
. Let
$L$
. Let
![]() $\unicode[STIX]{x1D6FE}$
be a topological generator of
$\unicode[STIX]{x1D6FE}$
be a topological generator of
![]() $\unicode[STIX]{x1D6E4}=\operatorname{Gal}(L_{\infty }/L)$
. For a positive integer
$\unicode[STIX]{x1D6E4}=\operatorname{Gal}(L_{\infty }/L)$
. For a positive integer
![]() $n$
, let
$n$
, let
![]() $\unicode[STIX]{x1D6E4}_{n}\subset \unicode[STIX]{x1D6E4}$
be the subgroup generated by
$\unicode[STIX]{x1D6E4}_{n}\subset \unicode[STIX]{x1D6E4}$
be the subgroup generated by
![]() $\unicode[STIX]{x1D6FE}^{p^{n}}$
and
$\unicode[STIX]{x1D6FE}^{p^{n}}$
and
![]() $L_{n}=L_{\infty }^{\langle \unicode[STIX]{x1D6FE}^{p^{n}}\rangle }$
be the subfield of
$L_{n}=L_{\infty }^{\langle \unicode[STIX]{x1D6FE}^{p^{n}}\rangle }$
be the subfield of
![]() $L_{\infty }$
fixed by
$L_{\infty }$
fixed by
![]() $\unicode[STIX]{x1D6E4}_{n}$
. We have
$\unicode[STIX]{x1D6E4}_{n}$
. We have
![]() $L_{\infty }=\bigcup _{n}L_{n}$
. Let
$L_{\infty }=\bigcup _{n}L_{n}$
. Let
![]() $L_{n}^{\prime }=L_{n}K$
and
$L_{n}^{\prime }=L_{n}K$
and
![]() $G_{n}^{\prime }=\operatorname{Gal}(\overline{L}/L_{n}^{\prime })$
.
$G_{n}^{\prime }=\operatorname{Gal}(\overline{L}/L_{n}^{\prime })$
.
Write
![]() ${\mathcal{R}}^{m}$
for the
${\mathcal{R}}^{m}$
for the
![]() ${\mathcal{R}}$
-module over which
${\mathcal{R}}$
-module over which
![]() $\operatorname{Gal}(\overline{K}/K)$
acts via
$\operatorname{Gal}(\overline{K}/K)$
acts via
![]() $\unicode[STIX]{x1D70F}$
. We define an action of
$\unicode[STIX]{x1D70F}$
. We define an action of
![]() $\operatorname{Gal}(\overline{K}/K)$
on
$\operatorname{Gal}(\overline{K}/K)$
on
![]() ${\mathcal{R}}^{m}\,\widehat{\otimes }_{L}\,\mathbb{C}_{p}$
by letting
${\mathcal{R}}^{m}\,\widehat{\otimes }_{L}\,\mathbb{C}_{p}$
by letting
![]() $\unicode[STIX]{x1D70E}\in \operatorname{Gal}(\overline{K}/K)$
send
$\unicode[STIX]{x1D70E}\in \operatorname{Gal}(\overline{K}/K)$
send
![]() $x\otimes y$
to
$x\otimes y$
to
![]() $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70E})(x)\otimes \unicode[STIX]{x1D70E}(y)$
. Then by [Reference SenSen93], there exists a matrix
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70E})(x)\otimes \unicode[STIX]{x1D70E}(y)$
. Then by [Reference SenSen93], there exists a matrix
![]() $M\in \operatorname{GL}_{m}\left({\mathcal{R}}\,\widehat{\otimes }_{L}\,\mathbb{C}_{p}\right)$
, an integer
$M\in \operatorname{GL}_{m}\left({\mathcal{R}}\,\widehat{\otimes }_{L}\,\mathbb{C}_{p}\right)$
, an integer
![]() $n\geqslant 0$
and a representation
$n\geqslant 0$
and a representation
![]() $\unicode[STIX]{x1D6FF}:\unicode[STIX]{x1D6E4}_{n}\rightarrow \operatorname{GL}_{m}({\mathcal{R}}\otimes _{L}L_{n}^{\prime })$
such that for all
$\unicode[STIX]{x1D6FF}:\unicode[STIX]{x1D6E4}_{n}\rightarrow \operatorname{GL}_{m}({\mathcal{R}}\otimes _{L}L_{n}^{\prime })$
such that for all
![]() $\unicode[STIX]{x1D70E}\in G_{n}^{\prime }$
we have
$\unicode[STIX]{x1D70E}\in G_{n}^{\prime }$
we have
Definition 7.6. The Sen operator associated with
![]() $\unicode[STIX]{x1D70F}$
is the element
$\unicode[STIX]{x1D70F}$
is the element
of
![]() $\operatorname{M}_{m}({\mathcal{R}}\,\widehat{\otimes }_{L}\,\mathbb{C}_{p})$
.
$\operatorname{M}_{m}({\mathcal{R}}\,\widehat{\otimes }_{L}\,\mathbb{C}_{p})$
.
The limit in the definitions always exists and is independent of the choice of
![]() $\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}$
and
![]() $M$
.
$M$
.
Now suppose that
![]() ${\mathcal{R}}=L$
and that
${\mathcal{R}}=L$
and that
![]() $\unicode[STIX]{x1D70F}$
is a Hodge–Tate representation with Hodge–Tate weights
$\unicode[STIX]{x1D70F}$
is a Hodge–Tate representation with Hodge–Tate weights
![]() $h_{1},h_{2},\ldots ,h_{m}$
. Let
$h_{1},h_{2},\ldots ,h_{m}$
. Let
![]() $\unicode[STIX]{x1D719}$
be the Sen operator associated with
$\unicode[STIX]{x1D719}$
be the Sen operator associated with
![]() $\unicode[STIX]{x1D70F}$
; it is an element of
$\unicode[STIX]{x1D70F}$
; it is an element of
![]() $\operatorname{M}_{m}(\mathbb{C}_{p})$
. The following theorem is a consequence of the results of [Reference SenSen80].
$\operatorname{M}_{m}(\mathbb{C}_{p})$
. The following theorem is a consequence of the results of [Reference SenSen80].
Theorem 7.7. The characteristic polynomial of
![]() $\unicode[STIX]{x1D719}$
is
$\unicode[STIX]{x1D719}$
is
![]() $\prod _{i=1}^{m}(X-h_{i})$
.
$\prod _{i=1}^{m}(X-h_{i})$
.
We restrict now to the case
![]() $L={\mathcal{R}}=\mathbb{Q}_{p}$
, so that
$L={\mathcal{R}}=\mathbb{Q}_{p}$
, so that
![]() $\unicode[STIX]{x1D70F}$
is a continuous representation
$\unicode[STIX]{x1D70F}$
is a continuous representation
![]() $\operatorname{Gal}(\overline{K}/K)\rightarrow \operatorname{GL}_{m}(\mathbb{Q}_{p})$
. Define a
$\operatorname{Gal}(\overline{K}/K)\rightarrow \operatorname{GL}_{m}(\mathbb{Q}_{p})$
. Define a
![]() $\mathbb{Q}_{p}$
-Lie algebra
$\mathbb{Q}_{p}$
-Lie algebra
![]() $\mathfrak{g}\subset \operatorname{M}_{m}(\mathbb{Q}_{p})$
by
$\mathfrak{g}\subset \operatorname{M}_{m}(\mathbb{Q}_{p})$
by
![]() $\mathfrak{g}=\mathbb{Q}_{p}\cdot \log (\unicode[STIX]{x1D70F}(\operatorname{Gal}(\overline{K}/K)))$
. We say that
$\mathfrak{g}=\mathbb{Q}_{p}\cdot \log (\unicode[STIX]{x1D70F}(\operatorname{Gal}(\overline{K}/K)))$
. We say that
![]() $\mathfrak{g}$
is the Lie algebra of
$\mathfrak{g}$
is the Lie algebra of
![]() $\unicode[STIX]{x1D70F}(\operatorname{Gal}(\overline{K}/K))$
. Let
$\unicode[STIX]{x1D70F}(\operatorname{Gal}(\overline{K}/K))$
. Let
![]() $\unicode[STIX]{x1D719}$
be the Sen operator associated with
$\unicode[STIX]{x1D719}$
be the Sen operator associated with
![]() $\unicode[STIX]{x1D70F}$
.
$\unicode[STIX]{x1D70F}$
.
Theorem 7.8 [Reference SenSen73, Theorem 1].
The Sen operator
![]() $\unicode[STIX]{x1D719}$
is an element of
$\unicode[STIX]{x1D719}$
is an element of
![]() $\mathfrak{g}\,\widehat{\otimes }_{\mathbb{Q}_{p}}\,\mathbb{C}_{p}$
.
$\mathfrak{g}\,\widehat{\otimes }_{\mathbb{Q}_{p}}\,\mathbb{C}_{p}$
.
Remark 7.9. The proof of Theorem 7.8 relies on the fact that
![]() $\unicode[STIX]{x1D70F}(\operatorname{Gal}(\overline{K}/K))$
is a finite-dimensional Lie group. It is doubtful that this proof can be generalized to the relative case.
$\unicode[STIX]{x1D70F}(\operatorname{Gal}(\overline{K}/K))$
is a finite-dimensional Lie group. It is doubtful that this proof can be generalized to the relative case.
7.3 The relative Sen operator associated with
 $\unicode[STIX]{x1D70C}_{r}$
$\unicode[STIX]{x1D70C}_{r}$
Fix a radius
![]() $r$
in the set
$r$
in the set
![]() $\{r_{i}\}\text{}_{i\in \mathbb{N}^{{>}0}}$
. Consider as usual the representation
$\{r_{i}\}\text{}_{i\in \mathbb{N}^{{>}0}}$
. Consider as usual the representation
![]() $\unicode[STIX]{x1D70C}_{r}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r,0})$
. We defined earlier a
$\unicode[STIX]{x1D70C}_{r}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r,0})$
. We defined earlier a
![]() $p$
-adic field
$p$
-adic field
![]() $K_{H_{r},p}$
. Write
$K_{H_{r},p}$
. Write
![]() $G_{K_{H_{r},p}}$
for its absolute Galois group. We look at the restriction
$G_{K_{H_{r},p}}$
for its absolute Galois group. We look at the restriction
![]() $\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}:G_{K_{H_{r},p}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r,0})$
as a representation with values in
$\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}:G_{K_{H_{r},p}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r,0})$
as a representation with values in
![]() $\operatorname{GL}_{4}(\mathbb{I}_{r,0})$
. Recall that
$\operatorname{GL}_{4}(\mathbb{I}_{r,0})$
. Recall that
![]() $\mathfrak{G}_{r}^{\operatorname{loc}}$
is the Lie algebra associated with the image of
$\mathfrak{G}_{r}^{\operatorname{loc}}$
is the Lie algebra associated with the image of
![]() $\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}$
. The goal of this section is to prove an analogue of Theorem 7.8 for this representation, i.e. to attach to
$\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}$
. The goal of this section is to prove an analogue of Theorem 7.8 for this representation, i.e. to attach to
![]() $\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}$
a ‘
$\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}$
a ‘
![]() $\mathbb{B}_{r}$
-Sen operator’ belonging to
$\mathbb{B}_{r}$
-Sen operator’ belonging to
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}$
. We start by constructing various Sen operators via Definition 7.6.
$\mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}$
. We start by constructing various Sen operators via Definition 7.6.
(i) The
 $\mathbb{Q}_{p}$
-algebra
$\mathbb{Q}_{p}$
-algebra
 $\mathbb{I}_{r,0}$
is complete for the
$\mathbb{I}_{r,0}$
is complete for the
 $p$
-adic topology. We associate with
$p$
-adic topology. We associate with
 $\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}$
a Sen operator
$\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}$
a Sen operator
 $\unicode[STIX]{x1D719}_{r}\in \operatorname{M}_{4}(\mathbb{I}_{r,0,\mathbb{C}_{p}})$
.
$\unicode[STIX]{x1D719}_{r}\in \operatorname{M}_{4}(\mathbb{I}_{r,0,\mathbb{C}_{p}})$
.(ii) Let
 $\mathfrak{a}\in S_{2}$
. Then
$\mathfrak{a}\in S_{2}$
. Then
 $\mathbb{I}_{r,0}/\mathfrak{a}$
is a finite-dimensional
$\mathbb{I}_{r,0}/\mathfrak{a}$
is a finite-dimensional
 $\mathbb{Q}_{p}$
-algebra. As usual write
$\mathbb{Q}_{p}$
-algebra. As usual write
 $\unicode[STIX]{x1D70B}_{\mathfrak{a}}:\mathbb{I}_{r,0}\rightarrow \mathbb{I}_{r,0}/\mathfrak{a}$
for the natural projection. Denote by
$\unicode[STIX]{x1D70B}_{\mathfrak{a}}:\mathbb{I}_{r,0}\rightarrow \mathbb{I}_{r,0}/\mathfrak{a}$
for the natural projection. Denote by
 $\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}$
the representation
$\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}$
the representation
 $\unicode[STIX]{x1D70B}_{\mathfrak{a}}\circ \,\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}:G_{K_{H_{r},p}}\rightarrow \operatorname{GL}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
. We associate with
$\unicode[STIX]{x1D70B}_{\mathfrak{a}}\circ \,\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}:G_{K_{H_{r},p}}\rightarrow \operatorname{GL}_{4}(\mathbb{I}_{r,0}/\mathfrak{a})$
. We associate with
 $\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}$
a Sen operator
$\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}$
a Sen operator
 $\unicode[STIX]{x1D719}_{r,\mathfrak{a}}\in \operatorname{M}_{4}((\mathbb{I}_{r,0}/\mathfrak{a})\,\widehat{\otimes }_{\mathbb{Q}_{p}}\,\mathbb{C}_{p})$
.
$\unicode[STIX]{x1D719}_{r,\mathfrak{a}}\in \operatorname{M}_{4}((\mathbb{I}_{r,0}/\mathfrak{a})\,\widehat{\otimes }_{\mathbb{Q}_{p}}\,\mathbb{C}_{p})$
.(iii) Let
 $\mathfrak{a}\in S_{2}$
. Let
$\mathfrak{a}\in S_{2}$
. Let
 $d$
be the
$d$
be the
 $\mathbb{Q}_{p}$
-dimension of
$\mathbb{Q}_{p}$
-dimension of
 $\mathbb{I}_{r,0}/\mathfrak{a}$
. Let
$\mathbb{I}_{r,0}/\mathfrak{a}$
. Let
 $k$
be a positive integer. An
$k$
be a positive integer. An
 $\mathbb{I}_{r,0}/\mathfrak{a}$
-linear endomorphism of
$\mathbb{I}_{r,0}/\mathfrak{a}$
-linear endomorphism of
 $(\mathbb{I}_{r,0}/\mathfrak{a})^{k}$
defines a
$(\mathbb{I}_{r,0}/\mathfrak{a})^{k}$
defines a
 $\mathbb{Q}_{p}$
-linear endomorphism of the underlying
$\mathbb{Q}_{p}$
-linear endomorphism of the underlying
 $\mathbb{Q}_{p}$
-vector space
$\mathbb{Q}_{p}$
-vector space
 $\mathbb{Q}_{p}^{kd}$
. This gives natural maps
$\mathbb{Q}_{p}^{kd}$
. This gives natural maps
 $\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}:\operatorname{M}_{k}(\mathbb{I}_{r,0}/\mathfrak{a})\rightarrow \operatorname{M}_{kd}(\mathbb{Q}_{p})$
and
$\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}:\operatorname{M}_{k}(\mathbb{I}_{r,0}/\mathfrak{a})\rightarrow \operatorname{M}_{kd}(\mathbb{Q}_{p})$
and
 $\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}^{\times }:\operatorname{GL}_{k}(\mathbb{I}_{r,0}/\mathfrak{a})\rightarrow \operatorname{GL}_{kd}(\mathbb{Q}_{p})$
(we leave the dependence of these morphisms on
$\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}^{\times }:\operatorname{GL}_{k}(\mathbb{I}_{r,0}/\mathfrak{a})\rightarrow \operatorname{GL}_{kd}(\mathbb{Q}_{p})$
(we leave the dependence of these morphisms on
 $k$
implicit). Choose
$k$
implicit). Choose
 $k=4$
and consider the representation
$k=4$
and consider the representation
 $\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}^{\times }\circ \,\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4d}(\mathbb{Q}_{p})$
. We associate with
$\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}^{\times }\circ \,\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4d}(\mathbb{Q}_{p})$
. We associate with
 $\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}$
a Sen operator
$\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}$
a Sen operator
 $\unicode[STIX]{x1D719}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}\in \operatorname{M}_{4d}(\mathbb{C}_{p})$
.
$\unicode[STIX]{x1D719}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}\in \operatorname{M}_{4d}(\mathbb{C}_{p})$
.
The operators constructed in constructions (i), (ii) and (iii) are related by the following lemma. We write
![]() $\unicode[STIX]{x1D70B}_{\mathfrak{a},\mathbb{C}_{p}}=\unicode[STIX]{x1D70B}_{\mathfrak{a}}\otimes 1:\mathbb{I}_{r,0,\mathbb{C}_{p}}\rightarrow \mathbb{I}_{r,0,\mathbb{C}_{p}}/\mathfrak{a}\mathbb{I}_{r,0,\mathbb{C}_{p}}$
. As above, we let
$\unicode[STIX]{x1D70B}_{\mathfrak{a},\mathbb{C}_{p}}=\unicode[STIX]{x1D70B}_{\mathfrak{a}}\otimes 1:\mathbb{I}_{r,0,\mathbb{C}_{p}}\rightarrow \mathbb{I}_{r,0,\mathbb{C}_{p}}/\mathfrak{a}\mathbb{I}_{r,0,\mathbb{C}_{p}}$
. As above, we let
![]() $d$
be the
$d$
be the
![]() $\mathbb{Q}_{p}$
-dimension of
$\mathbb{Q}_{p}$
-dimension of
![]() $\mathbb{I}_{r,0}/\mathfrak{a}$
. For every positive integer
$\mathbb{I}_{r,0}/\mathfrak{a}$
. For every positive integer
![]() $k$
, we set
$k$
, we set
![]() $\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}\otimes 1:\operatorname{M}_{k}(\mathbb{I}_{r,0,\mathbb{C}_{p}}/\mathfrak{a}\mathbb{I}_{r,0,\mathbb{C}_{p}})\rightarrow \operatorname{M}_{kd}(\mathbb{C}_{p})$
and
$\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}\otimes 1:\operatorname{M}_{k}(\mathbb{I}_{r,0,\mathbb{C}_{p}}/\mathfrak{a}\mathbb{I}_{r,0,\mathbb{C}_{p}})\rightarrow \operatorname{M}_{kd}(\mathbb{C}_{p})$
and
![]() $\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}^{\times }=\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}^{\times }\otimes 1:\operatorname{GL}_{k}(\mathbb{I}_{r,0,\mathbb{C}_{p}}/\mathfrak{a}\mathbb{I}_{r,0,\mathbb{C}_{p}})\rightarrow \operatorname{GL}_{kd}(\mathbb{C}_{p})$
.
$\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}^{\times }=\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}^{\times }\otimes 1:\operatorname{GL}_{k}(\mathbb{I}_{r,0,\mathbb{C}_{p}}/\mathfrak{a}\mathbb{I}_{r,0,\mathbb{C}_{p}})\rightarrow \operatorname{GL}_{kd}(\mathbb{C}_{p})$
.
Lemma 7.10. For every
![]() $\mathfrak{a}\in S_{2}$
, the following relations hold:
$\mathfrak{a}\in S_{2}$
, the following relations hold:
(i)
 $\unicode[STIX]{x1D719}_{r,\mathfrak{a}}=\unicode[STIX]{x1D70B}_{\mathfrak{a},\mathbb{C}_{p}}(\unicode[STIX]{x1D719}_{r})$
;
$\unicode[STIX]{x1D719}_{r,\mathfrak{a}}=\unicode[STIX]{x1D70B}_{\mathfrak{a},\mathbb{C}_{p}}(\unicode[STIX]{x1D719}_{r})$
;(ii)
 $\unicode[STIX]{x1D719}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}(\unicode[STIX]{x1D719}_{r,\mathfrak{a}})$
.
$\unicode[STIX]{x1D719}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}(\unicode[STIX]{x1D719}_{r,\mathfrak{a}})$
.
Proof. This can be checked directly from the construction of the Sen operator presented in §7.2. ◻
Recall that there is a natural inclusion
![]() $\unicode[STIX]{x1D704}_{\mathbb{B}_{r},\mathbb{C}_{p}}^{\prime }:\mathbb{I}_{r,0,\mathbb{C}_{p}}{\hookrightarrow}\mathbb{B}_{r,\mathbb{C}_{p}}$
. We define the
$\unicode[STIX]{x1D704}_{\mathbb{B}_{r},\mathbb{C}_{p}}^{\prime }:\mathbb{I}_{r,0,\mathbb{C}_{p}}{\hookrightarrow}\mathbb{B}_{r,\mathbb{C}_{p}}$
. We define the
![]() $\mathbb{B}_{r}$
-Sen operator attached to
$\mathbb{B}_{r}$
-Sen operator attached to
![]() $\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}$
as
$\unicode[STIX]{x1D70C}_{r}|_{G_{K_{H_{r},p}}}$
as
By definition,
![]() $\unicode[STIX]{x1D719}_{\mathbb{B}_{r}}$
is an element of
$\unicode[STIX]{x1D719}_{\mathbb{B}_{r}}$
is an element of
![]() $\operatorname{M}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
. Since
$\operatorname{M}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
. Since
![]() $\mathbb{B}_{r,\mathbb{C}_{p}}=\mathop{\varprojlim }\nolimits_{\mathfrak{a}\in S_{2}}\mathbb{I}_{r,0}/\mathfrak{a}$
, it is clear that
$\mathbb{B}_{r,\mathbb{C}_{p}}=\mathop{\varprojlim }\nolimits_{\mathfrak{a}\in S_{2}}\mathbb{I}_{r,0}/\mathfrak{a}$
, it is clear that
![]() $\unicode[STIX]{x1D719}_{\mathbb{B}_{r}}=\mathop{\varprojlim }\nolimits_{\mathfrak{a}\in S_{2}}\unicode[STIX]{x1D70B}_{\mathfrak{a},\mathbb{C}_{p}}(\unicode[STIX]{x1D719}_{r})$
. Then Lemma 7.10(i) implies that
$\unicode[STIX]{x1D719}_{\mathbb{B}_{r}}=\mathop{\varprojlim }\nolimits_{\mathfrak{a}\in S_{2}}\unicode[STIX]{x1D70B}_{\mathfrak{a},\mathbb{C}_{p}}(\unicode[STIX]{x1D719}_{r})$
. Then Lemma 7.10(i) implies that
Note that Theorem 7.8 can be applied only to representations with coefficients in
![]() $\mathbb{Q}_{p}$
, hence to construction (iii) above. However, we can use Lemma 7.10(ii) to show the following.
$\mathbb{Q}_{p}$
, hence to construction (iii) above. However, we can use Lemma 7.10(ii) to show the following.
Proposition 7.11. The operator
![]() $\unicode[STIX]{x1D719}_{\mathbb{B}_{r}}$
belongs to the Lie algebra
$\unicode[STIX]{x1D719}_{\mathbb{B}_{r}}$
belongs to the Lie algebra
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}$
. In particular, it belongs to
$\mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}$
. In particular, it belongs to
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}$
.
$\mathfrak{G}_{r,\mathbb{C}_{p}}$
.
Proof. For every
![]() $\mathfrak{a}\in S_{2}$
, let
$\mathfrak{a}\in S_{2}$
, let
![]() $d_{\mathfrak{a}}$
be the degree of the extension
$d_{\mathfrak{a}}$
be the degree of the extension
![]() $\mathbb{I}_{r,0}/\mathfrak{a}$
over
$\mathbb{I}_{r,0}/\mathfrak{a}$
over
![]() $\mathbb{Q}_{p}$
. Let
$\mathbb{Q}_{p}$
. Let
![]() $\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc},\mathbb{Q}_{p}}$
be the
$\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc},\mathbb{Q}_{p}}$
be the
![]() $\mathbb{Q}_{p}$
-Lie subalgebra of
$\mathbb{Q}_{p}$
-Lie subalgebra of
![]() $\operatorname{M}_{4d_{\mathfrak{a}}}(\mathbb{Q}_{p})$
associated with the image of
$\operatorname{M}_{4d_{\mathfrak{a}}}(\mathbb{Q}_{p})$
associated with the image of
![]() $\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}$
, defined by
$\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}$
, defined by
![]() $\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc},\mathbb{Q}_{p}}=\mathbb{Q}_{p}\cdot \log (\operatorname{Im}\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}})$
. Let
$\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc},\mathbb{Q}_{p}}=\mathbb{Q}_{p}\cdot \log (\operatorname{Im}\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}})$
. Let
![]() $\mathfrak{G}_{r,\mathfrak{a},\mathbb{C}_{p}}^{\operatorname{loc},\mathbb{Q}_{p}}=\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc},\mathbb{Q}_{p}}\,\widehat{\otimes }_{\mathbb{ Q}_{p}}\,\mathbb{C}_{p}$
. As
$\mathfrak{G}_{r,\mathfrak{a},\mathbb{C}_{p}}^{\operatorname{loc},\mathbb{Q}_{p}}=\mathfrak{G}_{r,\mathfrak{a}}^{\operatorname{loc},\mathbb{Q}_{p}}\,\widehat{\otimes }_{\mathbb{ Q}_{p}}\,\mathbb{C}_{p}$
. As
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}^{\times }(\operatorname{Im}\unicode[STIX]{x1D70C}_{r,\mathfrak{a}})$
, we can write
$\operatorname{Im}\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{Q}_{p}}^{\times }(\operatorname{Im}\unicode[STIX]{x1D70C}_{r,\mathfrak{a}})$
, we can write
The representation
![]() $\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}$
satisfies the assumptions of Theorem 7.8, so the Sen operator
$\unicode[STIX]{x1D70C}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}$
satisfies the assumptions of Theorem 7.8, so the Sen operator
![]() $\unicode[STIX]{x1D719}_{r,0,\mathfrak{a}}^{\mathbb{Q}_{p}}$
belongs to
$\unicode[STIX]{x1D719}_{r,0,\mathfrak{a}}^{\mathbb{Q}_{p}}$
belongs to
![]() $\mathfrak{G}_{r,\mathfrak{a},\mathbb{C}_{p}}^{\operatorname{loc},\mathbb{Q}_{p}}$
. By Lemma 7.10(ii)
$\mathfrak{G}_{r,\mathfrak{a},\mathbb{C}_{p}}^{\operatorname{loc},\mathbb{Q}_{p}}$
. By Lemma 7.10(ii)
![]() $\unicode[STIX]{x1D719}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}(\unicode[STIX]{x1D719}_{r,\mathfrak{a}})$
. Then (17) and the injectivity of
$\unicode[STIX]{x1D719}_{r,\mathfrak{a}}^{\mathbb{Q}_{p}}=\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}(\unicode[STIX]{x1D719}_{r,\mathfrak{a}})$
. Then (17) and the injectivity of
![]() $\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}$
give
$\unicode[STIX]{x1D6FC}_{\mathbb{C}_{p}}$
give
As
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}=\mathop{\varprojlim }\nolimits_{\mathfrak{ a}\in S_{2}}\mathfrak{G}_{r,\mathfrak{a},\mathbb{C}_{p}}^{\operatorname{loc}}$
, (16) and (18) imply that
$\mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}=\mathop{\varprojlim }\nolimits_{\mathfrak{ a}\in S_{2}}\mathfrak{G}_{r,\mathfrak{a},\mathbb{C}_{p}}^{\operatorname{loc}}$
, (16) and (18) imply that
![]() $\unicode[STIX]{x1D719}_{\mathbb{B}_{r}}\in \mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}$
.◻
$\unicode[STIX]{x1D719}_{\mathbb{B}_{r}}\in \mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}$
.◻
7.4 The exponential of the Sen operator
We use the work of the previous section to construct an element of
![]() $\operatorname{GL}_{4}(\mathbb{B}_{r})$
that has some specific eigenvalues and normalizes the Lie algebra
$\operatorname{GL}_{4}(\mathbb{B}_{r})$
that has some specific eigenvalues and normalizes the Lie algebra
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}$
. Such an element will be used in §8 to induce a
$\mathfrak{G}_{r,\mathbb{C}_{p}}^{\operatorname{loc}}$
. Such an element will be used in §8 to induce a
![]() $B_{r,\mathbb{C}_{p}}$
-module structure on some subalgebra of
$B_{r,\mathbb{C}_{p}}$
-module structure on some subalgebra of
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}$
, thus replacing the matrix ‘
$\mathfrak{G}_{r,\mathbb{C}_{p}}$
, thus replacing the matrix ‘
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})$
’ of [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15] that is not available in the non-ordinary setting.
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})$
’ of [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15] that is not available in the non-ordinary setting.
Let
![]() $\unicode[STIX]{x1D719}_{r}\in \operatorname{M}_{4}(\mathbb{I}_{r,0,\mathbb{C}_{p}})$
be the Sen operator defined in the previous section. We rescale it to define an element
$\unicode[STIX]{x1D719}_{r}\in \operatorname{M}_{4}(\mathbb{I}_{r,0,\mathbb{C}_{p}})$
be the Sen operator defined in the previous section. We rescale it to define an element
![]() $\unicode[STIX]{x1D719}_{r}^{\prime }=\log (u)\unicode[STIX]{x1D719}_{r}$
, where
$\unicode[STIX]{x1D719}_{r}^{\prime }=\log (u)\unicode[STIX]{x1D719}_{r}$
, where
![]() $u=1+p$
. Let
$u=1+p$
. Let
![]() $(T_{1},T_{2})$
be the images in
$(T_{1},T_{2})$
be the images in
![]() $A_{r}$
of the coordinate functions on the weight space. The logarithms and the exponentials in the following proposition are defined via the usual power series, that converge because of the assumption (exp) we made in the beginning of §7.
$A_{r}$
of the coordinate functions on the weight space. The logarithms and the exponentials in the following proposition are defined via the usual power series, that converge because of the assumption (exp) we made in the beginning of §7.
Lemma 7.12. The eigenvalues of
![]() $\unicode[STIX]{x1D719}_{r}^{\prime }$
are
$\unicode[STIX]{x1D719}_{r}^{\prime }$
are
![]() $0$
,
$0$
,
![]() $\log (u^{-2}(1+T_{2}))$
,
$\log (u^{-2}(1+T_{2}))$
,
![]() $\log (u^{-1}(1+T_{1}))$
and
$\log (u^{-1}(1+T_{1}))$
and
![]() $\log (u^{-3}(1+T_{1})(1+T_{2}))$
. In particular, the exponential series defines an element
$\log (u^{-3}(1+T_{1})(1+T_{2}))$
. In particular, the exponential series defines an element
![]() $\exp (\unicode[STIX]{x1D719}_{r}^{\prime })\in \operatorname{GL}_{4}(\mathbb{I}_{r,0,\mathbb{C}_{p}})$
, of eigenvalues
$\exp (\unicode[STIX]{x1D719}_{r}^{\prime })\in \operatorname{GL}_{4}(\mathbb{I}_{r,0,\mathbb{C}_{p}})$
, of eigenvalues
![]() $1$
,
$1$
,
![]() $u^{-2}(1+T_{2})$
,
$u^{-2}(1+T_{2})$
,
![]() $u^{-1}(1+T_{1})$
and
$u^{-1}(1+T_{1})$
and
![]() $u^{-3}(1+T_{1})(1+T_{2})$
.
$u^{-3}(1+T_{1})(1+T_{2})$
.
Proof. The
![]() $p$
-adic Galois representation
$p$
-adic Galois representation
![]() $\unicode[STIX]{x1D70C}_{f}$
associated with a classical eigenform
$\unicode[STIX]{x1D70C}_{f}$
associated with a classical eigenform
![]() $f$
of weight
$f$
of weight
![]() $(k_{1},k_{2})$
is Hodge–Tate with Hodge–Tate weights
$(k_{1},k_{2})$
is Hodge–Tate with Hodge–Tate weights
![]() $(0,k_{2}-2,k_{1}-1,k_{1}+k_{2}-3)$
. By Theorem 7.7 these weights are the eigenvalues of the Sen operator
$(0,k_{2}-2,k_{1}-1,k_{1}+k_{2}-3)$
. By Theorem 7.7 these weights are the eigenvalues of the Sen operator
![]() $\unicode[STIX]{x1D719}_{f}$
associated with
$\unicode[STIX]{x1D719}_{f}$
associated with
![]() $\unicode[STIX]{x1D70C}_{f}$
. By Lemma 7.10(i), the eigenvalues of
$\unicode[STIX]{x1D70C}_{f}$
. By Lemma 7.10(i), the eigenvalues of
![]() $\unicode[STIX]{x1D719}_{r}$
interpolate those of the operators
$\unicode[STIX]{x1D719}_{r}$
interpolate those of the operators
![]() $\unicode[STIX]{x1D719}_{f}$
when
$\unicode[STIX]{x1D719}_{f}$
when
![]() $f$
varies in the set of classical points of
$f$
varies in the set of classical points of
![]() $A_{r}$
. As such points form a Zariski-dense subset of
$A_{r}$
. As such points form a Zariski-dense subset of
![]() $\operatorname{Spec}A_{r}$
, the interpolation is unique and can be easily computed. The lemma follows from this.◻
$\operatorname{Spec}A_{r}$
, the interpolation is unique and can be easily computed. The lemma follows from this.◻
Let
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}=\unicode[STIX]{x1D704}_{\mathbb{B}_{r,\mathbb{C}_{p}}}(\exp (\unicode[STIX]{x1D719}_{r,0}^{\prime }))$
. By definition,
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}=\unicode[STIX]{x1D704}_{\mathbb{B}_{r,\mathbb{C}_{p}}}(\exp (\unicode[STIX]{x1D719}_{r,0}^{\prime }))$
. By definition,
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
is an element of
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
is an element of
![]() $\operatorname{GL}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
. We show that it has the two properties we need. We define a matrix
$\operatorname{GL}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
. We show that it has the two properties we need. We define a matrix
![]() $C_{T_{1},T_{2}}\in \operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
by
$C_{T_{1},T_{2}}\in \operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
by
Proposition 7.13.
(i) There exists
 $\unicode[STIX]{x1D6FE}\in \operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
satisfying
$\unicode[STIX]{x1D6FE}\in \operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
satisfying
 $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}=\unicode[STIX]{x1D6FE}C_{T_{1},T_{2}}\unicode[STIX]{x1D6FE}^{-1}$
.
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}=\unicode[STIX]{x1D6FE}C_{T_{1},T_{2}}\unicode[STIX]{x1D6FE}^{-1}$
.(ii) The element
 $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
normalizes the Lie algebra
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
normalizes the Lie algebra
 $\mathfrak{G}_{r,\mathbb{C}_{p}}$
.
$\mathfrak{G}_{r,\mathbb{C}_{p}}$
.
Proof. The matrices
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
and
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
and
![]() $C_{T_{1},T_{2}}$
have the same eigenvalues by Lemma 7.12. Hence, there exists
$C_{T_{1},T_{2}}$
have the same eigenvalues by Lemma 7.12. Hence, there exists
![]() $\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
satisfying the equality of part (i) if and only if the difference between any two of the eigenvalues of
$\unicode[STIX]{x1D6FE}\in \operatorname{GL}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
satisfying the equality of part (i) if and only if the difference between any two of the eigenvalues of
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
is invertible in
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
is invertible in
![]() $\mathbb{B}_{r}$
. We check by a direct calculation that each of these differences belongs to an ideal of the form
$\mathbb{B}_{r}$
. We check by a direct calculation that each of these differences belongs to an ideal of the form
![]() $P\cdot \mathbb{B}_{r}$
with
$P\cdot \mathbb{B}_{r}$
with
![]() $P\in S^{\operatorname{bad}}$
, hence it is invertible in
$P\in S^{\operatorname{bad}}$
, hence it is invertible in
![]() $\mathbb{B}_{r}$
by Remark 7.4. As both
$\mathbb{B}_{r}$
by Remark 7.4. As both
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
and
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
and
![]() $C_{T_{1},T_{2}}$
are elements of
$C_{T_{1},T_{2}}$
are elements of
![]() $\operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
, we can take
$\operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
, we can take
![]() $\unicode[STIX]{x1D6FE}\in \operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
.
$\unicode[STIX]{x1D6FE}\in \operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
.
Part (ii) follows from Proposition 7.11. ◻
8 Existence of a Galois level in the residual symmetric cube and full cases
We have all the ingredients we need to state and prove our first main theorem. Let
![]() $h\in \mathbb{Q}^{+,\times }$
. Let
$h\in \mathbb{Q}^{+,\times }$
. Let
![]() $\mathbb{T}_{h}$
be a local component of the
$\mathbb{T}_{h}$
be a local component of the
![]() $h$
-adapted Hecke algebra of genus
$h$
-adapted Hecke algebra of genus
![]() $2$
and level
$2$
and level
![]() $\unicode[STIX]{x1D6E4}_{1}(M)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
. Suppose that condition (exp) of §7 is satisfied and that the residual Galois representation
$\unicode[STIX]{x1D6E4}_{1}(M)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
. Suppose that condition (exp) of §7 is satisfied and that the residual Galois representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}_{h}}$
associated with
$\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}_{h}}$
associated with
![]() $\mathbb{T}_{h}$
is either full or of symmetric cube type in the sense of Definition 3.11. Let
$\mathbb{T}_{h}$
is either full or of symmetric cube type in the sense of Definition 3.11. Let
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a family, i.e. the morphism of finite
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
be a family, i.e. the morphism of finite
![]() $\unicode[STIX]{x1D6EC}_{h}$
-algebras describing an irreducible component of
$\unicode[STIX]{x1D6EC}_{h}$
-algebras describing an irreducible component of
![]() $\mathbb{T}_{h}$
. Let
$\mathbb{T}_{h}$
. Let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the Galois representation associated with
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the Galois representation associated with
![]() $\unicode[STIX]{x1D703}$
. Suppose that
$\unicode[STIX]{x1D703}$
. Suppose that
![]() $\unicode[STIX]{x1D70C}$
is
$\unicode[STIX]{x1D70C}$
is
![]() $\mathbb{Z}_{p}$
-regular in the sense of Definition 3.10. For every radius
$\mathbb{Z}_{p}$
-regular in the sense of Definition 3.10. For every radius
![]() $r$
in the set
$r$
in the set
![]() $\{r_{i}\}\text{}_{i\in \mathbb{N}^{{>}0}}$
defined in §4, let
$\{r_{i}\}\text{}_{i\in \mathbb{N}^{{>}0}}$
defined in §4, let
![]() $\mathfrak{G}_{r}$
be the Lie algebra that we attached to
$\mathfrak{G}_{r}$
be the Lie algebra that we attached to
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}$
in §7.1.
$\operatorname{Im}\unicode[STIX]{x1D70C}$
in §7.1.
Theorem 8.1. There exists a non-zero ideal
![]() $\mathfrak{l}$
of
$\mathfrak{l}$
of
![]() $\mathbb{I}_{0}$
such that
$\mathbb{I}_{0}$
such that
for every
![]() $r\in \{r_{i}\}\text{}_{i\in \mathbb{N}^{{>}0}}$
.
$r\in \{r_{i}\}\text{}_{i\in \mathbb{N}^{{>}0}}$
.
Let
![]() $\unicode[STIX]{x1D6E5}$
be the set of roots of
$\unicode[STIX]{x1D6E5}$
be the set of roots of
![]() $\operatorname{GSp}_{4}$
with respect to our choice of maximal torus. Recall that for
$\operatorname{GSp}_{4}$
with respect to our choice of maximal torus. Recall that for
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
we denote by
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
we denote by
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}}$
the nilpotent subalgebra of
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}}$
the nilpotent subalgebra of
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}$
corresponding to
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}$
corresponding to
![]() $\unicode[STIX]{x1D6FC}$
. Let
$\unicode[STIX]{x1D6FC}$
. Let
![]() $r$
be a radius in the set
$r$
be a radius in the set
![]() $\{r_{i}\}\text{}_{i\geqslant 1}$
. We set
$\{r_{i}\}\text{}_{i\geqslant 1}$
. We set
![]() $\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}=\mathfrak{G}_{r}\cap \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r})$
and
$\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}=\mathfrak{G}_{r}\cap \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r})$
and
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC}}=\mathfrak{G}_{r,\mathbb{C}_{p}}\cap \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
, which coincides with
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC}}=\mathfrak{G}_{r,\mathbb{C}_{p}}\cap \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
, which coincides with
![]() $\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}\,\widehat{\otimes }_{\mathbb{Q}_{p}}\,\mathbb{C}_{p}$
. Via the isomorphisms
$\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}\,\widehat{\otimes }_{\mathbb{Q}_{p}}\,\mathbb{C}_{p}$
. Via the isomorphisms
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r})\cong \mathbb{B}_{r}$
and
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r})\cong \mathbb{B}_{r}$
and
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r,\mathbb{C}_{p}})\cong \mathbb{B}_{r,\mathbb{C}_{p}}$
, we see
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r,\mathbb{C}_{p}})\cong \mathbb{B}_{r,\mathbb{C}_{p}}$
, we see
![]() $\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
as a
$\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
as a
![]() $\mathbb{Q}_{p}$
-vector subspace of
$\mathbb{Q}_{p}$
-vector subspace of
![]() $\mathbb{B}_{r}$
and
$\mathbb{B}_{r}$
and
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC}}$
as a
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC}}$
as a
![]() $\mathbb{C}_{p}$
-vector subspace of
$\mathbb{C}_{p}$
-vector subspace of
![]() $\mathbb{B}_{r,\mathbb{C}_{p}}$
.
$\mathbb{B}_{r,\mathbb{C}_{p}}$
.
Recall that
![]() $U^{\unicode[STIX]{x1D6FC}}$
denotes the one-parameter unipotent subgroup of
$U^{\unicode[STIX]{x1D6FC}}$
denotes the one-parameter unipotent subgroup of
![]() $\operatorname{GSp}_{4}$
associated with the root
$\operatorname{GSp}_{4}$
associated with the root
![]() $\unicode[STIX]{x1D6FC}$
. Let
$\unicode[STIX]{x1D6FC}$
. Let
![]() $H_{r}$
be the normal open subgroup of
$H_{r}$
be the normal open subgroup of
![]() $G_{\mathbb{Q}}$
defined in the beginning of §7. Note that Proposition 6.14 holds with
$G_{\mathbb{Q}}$
defined in the beginning of §7. Note that Proposition 6.14 holds with
![]() $\unicode[STIX]{x1D70C}|_{H_{0}}$
replaced by
$\unicode[STIX]{x1D70C}|_{H_{0}}$
replaced by
![]() $\unicode[STIX]{x1D70C}|_{H_{r}}$
because
$\unicode[STIX]{x1D70C}|_{H_{r}}$
because
![]() $H_{r}$
is open in
$H_{r}$
is open in
![]() $G_{\mathbb{Q}}$
. Let
$G_{\mathbb{Q}}$
. Let
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{r}})=U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })\cap \unicode[STIX]{x1D70C}(H_{r})$
and
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{r}})=U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0}^{\circ })\cap \unicode[STIX]{x1D70C}(H_{r})$
and
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}_{r})=U^{\unicode[STIX]{x1D6FC}}\cap \unicode[STIX]{x1D70C}_{r}(H_{r})$
. Via the isomorphisms
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}_{r})=U^{\unicode[STIX]{x1D6FC}}\cap \unicode[STIX]{x1D70C}_{r}(H_{r})$
. Via the isomorphisms
![]() $U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0})\cong \mathbb{I}_{0}$
and
$U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0})\cong \mathbb{I}_{0}$
and
![]() $U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{r,0})\cong \mathbb{I}_{r,0}$
we identify
$U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{r,0})\cong \mathbb{I}_{r,0}$
we identify
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{0}})$
and
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{0}})$
and
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}_{r})$
with
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}_{r})$
with
![]() $\mathbb{Z}_{p}$
-submodules of
$\mathbb{Z}_{p}$
-submodules of
![]() $\mathbb{I}_{0}$
and
$\mathbb{I}_{0}$
and
![]() $\mathbb{I}_{r,0}$
, respectively. Note that the injection
$\mathbb{I}_{r,0}$
, respectively. Note that the injection
![]() $\mathbb{I}_{0}^{\circ }{\hookrightarrow}\mathbb{I}_{r,0}^{\circ }$
induces an isomorphism of
$\mathbb{I}_{0}^{\circ }{\hookrightarrow}\mathbb{I}_{r,0}^{\circ }$
induces an isomorphism of
![]() $\mathbb{Z}_{p}$
-modules
$\mathbb{Z}_{p}$
-modules
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{0}})\cong U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}_{r})$
.
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{0}})\cong U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}_{r})$
.
We define a nilpotent subalgebra of
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0})$
by
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0})$
by
![]() $\mathfrak{U}_{\mathbb{I}_{r,0}}^{\unicode[STIX]{x1D6FC}}=\mathbb{Q}_{p}\cdot \log (U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}_{r}))$
. We identify
$\mathfrak{U}_{\mathbb{I}_{r,0}}^{\unicode[STIX]{x1D6FC}}=\mathbb{Q}_{p}\cdot \log (U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}_{r}))$
. We identify
![]() $\mathfrak{U}_{\mathbb{I}_{r,0}}^{\unicode[STIX]{x1D6FC}}$
with a
$\mathfrak{U}_{\mathbb{I}_{r,0}}^{\unicode[STIX]{x1D6FC}}$
with a
![]() $\mathbb{Q}_{p}$
-vector subspace of
$\mathbb{Q}_{p}$
-vector subspace of
![]() $\mathbb{I}_{r,0}$
. Note that the natural injection
$\mathbb{I}_{r,0}$
. Note that the natural injection
![]() $\unicode[STIX]{x1D704}_{\mathbb{B}_{r}}:\mathbb{I}_{r,0}{\hookrightarrow}\mathbb{B}_{r}$
induces an injection
$\unicode[STIX]{x1D704}_{\mathbb{B}_{r}}:\mathbb{I}_{r,0}{\hookrightarrow}\mathbb{B}_{r}$
induces an injection
![]() $\mathfrak{U}_{\mathbb{I}_{r,0}}^{\unicode[STIX]{x1D6FC}}{\hookrightarrow}\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
for every
$\mathfrak{U}_{\mathbb{I}_{r,0}}^{\unicode[STIX]{x1D6FC}}{\hookrightarrow}\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
for every
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Lemma 8.2. For every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
and every
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
and every
![]() $r$
, there exists a non-zero ideal
$r$
, there exists a non-zero ideal
![]() $\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
of
$\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
of
![]() $\mathbb{I}_{0}$
, independent of
$\mathbb{I}_{0}$
, independent of
![]() $r$
, such that the
$r$
, such that the
![]() $B_{r}$
-span of
$B_{r}$
-span of
![]() $\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
contains
$\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
contains
![]() $\mathfrak{l}^{\unicode[STIX]{x1D6FC}}\mathbb{B}_{r}$
.
$\mathfrak{l}^{\unicode[STIX]{x1D6FC}}\mathbb{B}_{r}$
.
Proof. Let
![]() $d$
be the dimension of
$d$
be the dimension of
![]() $Q(\mathbb{I}_{0}^{\circ })$
over
$Q(\mathbb{I}_{0}^{\circ })$
over
![]() $Q(\unicode[STIX]{x1D6EC}_{h})$
. Let
$Q(\unicode[STIX]{x1D6EC}_{h})$
. Let
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. By Proposition 6.14 the unipotent subgroup
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. By Proposition 6.14 the unipotent subgroup
![]() $U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{r}})$
contains a basis
$U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{r}})$
contains a basis
![]() $E=\{e_{i}\}\text{}_{i=1,\ldots ,d}$
of a
$E=\{e_{i}\}\text{}_{i=1,\ldots ,d}$
of a
![]() $\unicode[STIX]{x1D6EC}_{h}$
-lattice in
$\unicode[STIX]{x1D6EC}_{h}$
-lattice in
![]() $\mathbb{I}_{0}^{\circ }$
. Lemma 6.6 implies that the
$\mathbb{I}_{0}^{\circ }$
. Lemma 6.6 implies that the
![]() $\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
-span of
$\unicode[STIX]{x1D6EC}_{h}[p^{-1}]$
-span of
![]() $E$
contains a non-zero ideal
$E$
contains a non-zero ideal
![]() $\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
of
$\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
of
![]() $\mathbb{I}_{0}$
. Consider the map
$\mathbb{I}_{0}$
. Consider the map
![]() $\unicode[STIX]{x1D704}^{\unicode[STIX]{x1D6FC}}:U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0})\rightarrow \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r})$
given by the composition
$\unicode[STIX]{x1D704}^{\unicode[STIX]{x1D6FC}}:U^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0})\rightarrow \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r})$
given by the composition
where all the maps have been introduced above. Note that
![]() $\unicode[STIX]{x1D704}^{\unicode[STIX]{x1D6FC}}(U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{0}}))\subset \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
. Let
$\unicode[STIX]{x1D704}^{\unicode[STIX]{x1D6FC}}(U^{\unicode[STIX]{x1D6FC}}(\unicode[STIX]{x1D70C}|_{H_{0}}))\subset \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
. Let
![]() $E_{\mathbb{B}_{r}}=\unicode[STIX]{x1D704}^{\unicode[STIX]{x1D6FC}}(E)$
. As
$E_{\mathbb{B}_{r}}=\unicode[STIX]{x1D704}^{\unicode[STIX]{x1D6FC}}(E)$
. As
![]() $\unicode[STIX]{x1D704}^{\unicode[STIX]{x1D6FC}}$
is a morphism of
$\unicode[STIX]{x1D704}^{\unicode[STIX]{x1D6FC}}$
is a morphism of
![]() $\mathbb{I}_{0}$
-modules we have
$\mathbb{I}_{0}$
-modules we have
By construction and by Remark 7.2, the ideal
![]() $\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
can be chosen independently of
$\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
can be chosen independently of
![]() $r$
.◻
$r$
.◻
Let
![]() $\unicode[STIX]{x1D6FE}$
be an element of
$\unicode[STIX]{x1D6FE}$
be an element of
![]() $\operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
such that
$\operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
such that
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}=\unicode[STIX]{x1D6FE}C_{T_{1},T_{2}}\unicode[STIX]{x1D6FE}^{-1}$
; it exists by Proposition 7.13(i). Let
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}=\unicode[STIX]{x1D6FE}C_{T_{1},T_{2}}\unicode[STIX]{x1D6FE}^{-1}$
; it exists by Proposition 7.13(i). Let
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FE}^{-1}\mathfrak{G}_{r,\mathbb{C}_{p}}\unicode[STIX]{x1D6FE}$
. For each
$\mathfrak{G}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE}}=\unicode[STIX]{x1D6FE}^{-1}\mathfrak{G}_{r,\mathbb{C}_{p}}\unicode[STIX]{x1D6FE}$
. For each
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, let
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}=\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r,\mathbb{C}_{p}})\cap \mathfrak{G}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE}}$
. We prove the following lemma by an argument similar to that of [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, Theorem 4.8].
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}=\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{B}_{r,\mathbb{C}_{p}})\cap \mathfrak{G}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE}}$
. We prove the following lemma by an argument similar to that of [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, Theorem 4.8].
Lemma 8.3. For every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, the Lie algebra
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
, the Lie algebra
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}$
is a
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}$
is a
![]() $B_{r,\mathbb{C}_{p}}$
-submodule of
$B_{r,\mathbb{C}_{p}}$
-submodule of
![]() $\mathbb{B}_{r,\mathbb{C}_{p}}$
.
$\mathbb{B}_{r,\mathbb{C}_{p}}$
.
Proof. By Proposition 7.13(ii), the operator
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
normalizes
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}$
normalizes
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}$
, hence
$\mathfrak{G}_{r,\mathbb{C}_{p}}$
, hence
![]() $C_{T_{1},T_{2}}$
normalizes
$C_{T_{1},T_{2}}$
normalizes
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE}}$
. Let
$\mathfrak{G}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE}}$
. Let
![]() $\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{1}$
and
![]() $\unicode[STIX]{x1D6FC}_{2}$
be the roots sending
$\unicode[STIX]{x1D6FC}_{2}$
be the roots sending
![]() $\operatorname{diag}(t_{1},t_{2},\unicode[STIX]{x1D708}t_{2}^{-1},\unicode[STIX]{x1D708}t_{1}^{-1})\in T_{2}$
to
$\operatorname{diag}(t_{1},t_{2},\unicode[STIX]{x1D708}t_{2}^{-1},\unicode[STIX]{x1D708}t_{1}^{-1})\in T_{2}$
to
![]() $t_{1}/t_{2}$
and
$t_{1}/t_{2}$
and
![]() $\unicode[STIX]{x1D708}^{-1}t_{2}^{2}$
, respectively. With respect to our choice of Borel subgroup, the set of positive roots of
$\unicode[STIX]{x1D708}^{-1}t_{2}^{2}$
, respectively. With respect to our choice of Borel subgroup, the set of positive roots of
![]() $\operatorname{GSp}_{4}$
is
$\operatorname{GSp}_{4}$
is
![]() $\{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2},2\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}\}$
. Conjugation by
$\{\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2},2\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}\}$
. Conjugation by
![]() $C_{T_{1},T_{2}}$
on the
$C_{T_{1},T_{2}}$
on the
![]() $\mathbb{C}_{p}$
-vector space
$\mathbb{C}_{p}$
-vector space
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
induces multiplication by
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
induces multiplication by
![]() $\unicode[STIX]{x1D6FC}_{1}(C_{T_{1},T_{2}})=u^{-2}(1+T_{2})$
. As
$\unicode[STIX]{x1D6FC}_{1}(C_{T_{1},T_{2}})=u^{-2}(1+T_{2})$
. As
![]() $u^{-2}\in \mathbb{Z}_{p}^{\times }$
and
$u^{-2}\in \mathbb{Z}_{p}^{\times }$
and
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}}$
is stable under
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}}$
is stable under
![]() $\operatorname{Ad}(C_{T_{1},T_{2}})$
, multiplication by
$\operatorname{Ad}(C_{T_{1},T_{2}})$
, multiplication by
![]() $1+T_{2}$
on
$1+T_{2}$
on
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
leaves
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
leaves
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}}$
stable. Now we compute
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}}$
stable. Now we compute
where the inclusion
![]() $(1+T_{2})\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}}\subset \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}}$
is the result of the previous sentence. Similarly, conjugation by
$(1+T_{2})\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}}\subset \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}}$
is the result of the previous sentence. Similarly, conjugation by
![]() $C_{T_{1},T_{2}}$
on the
$C_{T_{1},T_{2}}$
on the
![]() $\mathbb{C}_{p}$
-vector space
$\mathbb{C}_{p}$
-vector space
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
induces multiplication by
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
induces multiplication by
![]() $\unicode[STIX]{x1D6FC}_{2}(C_{T_{1},T_{2}})=u\cdot (1+T_{1})/(1+T_{2})$
. As
$\unicode[STIX]{x1D6FC}_{2}(C_{T_{1},T_{2}})=u\cdot (1+T_{1})/(1+T_{2})$
. As
![]() $u\in \mathbb{Z}_{p}^{\times }$
and
$u\in \mathbb{Z}_{p}^{\times }$
and
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{2}}$
is stable under
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{2}}$
is stable under
![]() $\operatorname{Ad}(C_{T_{1},T_{2}})$
, multiplication by
$\operatorname{Ad}(C_{T_{1},T_{2}})$
, multiplication by
![]() $1+T_{2}$
on
$1+T_{2}$
on
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
leaves
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
leaves
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{2}}$
stable. The same calculation as above shows that multiplication by
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{2}}$
stable. The same calculation as above shows that multiplication by
![]() $(1+T_{1})/(1+T_{2})$
on
$(1+T_{1})/(1+T_{2})$
on
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
leaves
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
leaves
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
stable. We deduce that multiplication by
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
stable. We deduce that multiplication by
![]() $1+T_{1}$
also leaves
$1+T_{1}$
also leaves
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
stable. As
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
stable. As
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
is a
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
is a
![]() $\mathbb{C}_{p}$
-vector space, the
$\mathbb{C}_{p}$
-vector space, the
![]() $\mathbb{C}_{p}[T_{1},T_{2}]$
-module structure on
$\mathbb{C}_{p}[T_{1},T_{2}]$
-module structure on
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
induces a
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
induces a
![]() $\mathbb{C}_{p}[T_{1},T_{2}]$
-module structure on
$\mathbb{C}_{p}[T_{1},T_{2}]$
-module structure on
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
. With respect to the
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
. With respect to the
![]() $p$
-adic topology
$p$
-adic topology
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
is complete and
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
is complete and
![]() $\mathbb{C}_{p}[T_{1},T_{2}]$
is dense in
$\mathbb{C}_{p}[T_{1},T_{2}]$
is dense in
![]() $B_{r,\mathbb{C}_{p}}$
, so the
$B_{r,\mathbb{C}_{p}}$
, so the
![]() $B_{r,\mathbb{C}_{p}}$
-module structure on
$B_{r,\mathbb{C}_{p}}$
-module structure on
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
induces a
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}(\mathbb{B}_{r,\mathbb{C}_{p}})$
induces a
![]() $B_{r,\mathbb{C}_{p}}$
-module structure on
$B_{r,\mathbb{C}_{p}}$
-module structure on
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
.
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
.
If
![]() $\unicode[STIX]{x1D6FD}$
is any root, we can write
$\unicode[STIX]{x1D6FD}$
is any root, we can write
 $$\begin{eqnarray}\displaystyle B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}} & = & \displaystyle B_{r,\mathbb{C}_{p}}\cdot [\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}},\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}}]\nonumber\\ \displaystyle & \subset & \displaystyle [B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}},\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}}]\subset [\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}},\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}}]=\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}} & = & \displaystyle B_{r,\mathbb{C}_{p}}\cdot [\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}},\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}}]\nonumber\\ \displaystyle & \subset & \displaystyle [B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}},\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}}]\subset [\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}},\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}}]=\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FD}},\nonumber\end{eqnarray}$$
where the inclusion
![]() $B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}\subset \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
is the result of the previous paragraph.◻
$B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}\subset \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}}$
is the result of the previous paragraph.◻
Proof of Theorem 8.1.
Let
![]() $E_{\mathbb{B}_{r}}\subset \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
be the set defined in the proof of Lemma 8.2. Let
$E_{\mathbb{B}_{r}}\subset \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
be the set defined in the proof of Lemma 8.2. Let
![]() $E_{\mathbb{B}_{r},\mathbb{C}_{p}}=\{e\otimes 1\,|\,e\in E_{\mathbb{B}_{r}}\}\subset \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC}}$
. Consider the Lie subalgebra
$E_{\mathbb{B}_{r},\mathbb{C}_{p}}=\{e\otimes 1\,|\,e\in E_{\mathbb{B}_{r}}\}\subset \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC}}$
. Consider the Lie subalgebra
![]() $B_{r,\mathbb{C}_{p}}\cdot \mathfrak{G}_{r,\mathbb{C}_{p}}$
of
$B_{r,\mathbb{C}_{p}}\cdot \mathfrak{G}_{r,\mathbb{C}_{p}}$
of
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
. For every
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
. For every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
we have
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
we have
![]() $B_{r,\mathbb{C}_{p}}\cdot \mathfrak{G}_{r,\mathbb{C}_{p}}\cap \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(B_{r,\mathbb{C}_{p}})=B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
. By Lemma 8.2 there exists an ideal
$B_{r,\mathbb{C}_{p}}\cdot \mathfrak{G}_{r,\mathbb{C}_{p}}\cap \mathfrak{u}^{\unicode[STIX]{x1D6FC}}(B_{r,\mathbb{C}_{p}})=B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
. By Lemma 8.2 there exists an ideal
![]() $\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
of
$\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
of
![]() $\mathbb{I}_{0}$
, independent of
$\mathbb{I}_{0}$
, independent of
![]() $r$
, such that
$r$
, such that
![]() $\mathfrak{l}^{\unicode[STIX]{x1D6FC}}\cdot \mathbb{B}_{r,\mathbb{C}_{p}}\subset B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
. Let
$\mathfrak{l}^{\unicode[STIX]{x1D6FC}}\cdot \mathbb{B}_{r,\mathbb{C}_{p}}\subset B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
. Let
![]() $\mathfrak{l}_{0}=\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
. Then Lemma 6.11 gives an inclusion
$\mathfrak{l}_{0}=\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
. Then Lemma 6.11 gives an inclusion
As before, let
![]() $\unicode[STIX]{x1D6FE}$
be an element of
$\unicode[STIX]{x1D6FE}$
be an element of
![]() $\operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
satisfying
$\operatorname{GSp}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
satisfying
![]() $\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}=\unicode[STIX]{x1D6FE}C_{T_{1},T_{2}}\unicode[STIX]{x1D6FE}^{-1}$
. The Lie algebra
$\unicode[STIX]{x1D6F7}_{\mathbb{B}_{r}}=\unicode[STIX]{x1D6FE}C_{T_{1},T_{2}}\unicode[STIX]{x1D6FE}^{-1}$
. The Lie algebra
![]() $\mathfrak{l}_{0}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
is stable under
$\mathfrak{l}_{0}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})$
is stable under
![]() $\operatorname{Ad}(\unicode[STIX]{x1D6FE}^{-1})$
, so (20) implies that
$\operatorname{Ad}(\unicode[STIX]{x1D6FE}^{-1})$
, so (20) implies that
![]() $\mathfrak{l}_{0}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})=\unicode[STIX]{x1D6FE}^{-1}(\mathfrak{l}_{0}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}}))\unicode[STIX]{x1D6FE}\subset \unicode[STIX]{x1D6FE}^{-1}(B_{r,\mathbb{C}_{p}}\cdot \mathfrak{G}_{r})\unicode[STIX]{x1D6FE}=B_{r,\mathbb{C}_{p}}\cdot \unicode[STIX]{x1D6FE}^{-1}\mathfrak{G}_{r}\unicode[STIX]{x1D6FE}=B_{r,\mathbb{C}_{p}}\cdot \mathfrak{G}_{r}^{\unicode[STIX]{x1D6FE}}$
. We deduce that, for every
$\mathfrak{l}_{0}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})=\unicode[STIX]{x1D6FE}^{-1}(\mathfrak{l}_{0}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}}))\unicode[STIX]{x1D6FE}\subset \unicode[STIX]{x1D6FE}^{-1}(B_{r,\mathbb{C}_{p}}\cdot \mathfrak{G}_{r})\unicode[STIX]{x1D6FE}=B_{r,\mathbb{C}_{p}}\cdot \unicode[STIX]{x1D6FE}^{-1}\mathfrak{G}_{r}\unicode[STIX]{x1D6FE}=B_{r,\mathbb{C}_{p}}\cdot \mathfrak{G}_{r}^{\unicode[STIX]{x1D6FE}}$
. We deduce that, for every
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
,
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
,
By Lemma 8.3
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}$
is a
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}}$
is a
![]() $B_{r,\mathbb{C}_{p}}$
-submodule of
$B_{r,\mathbb{C}_{p}}$
-submodule of
![]() $\mathfrak{u}_{r}(\mathbb{B}_{r,\mathbb{C}_{p}})$
, so
$\mathfrak{u}_{r}(\mathbb{B}_{r,\mathbb{C}_{p}})$
, so
![]() $B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}=\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}$
. Hence, (21) gives
$B_{r,\mathbb{C}_{p}}\cdot \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}=\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}$
. Hence, (21) gives
for every
![]() $\unicode[STIX]{x1D6FC}$
. Set
$\unicode[STIX]{x1D6FC}$
. Set
![]() $\mathfrak{l}_{1}=\mathfrak{l}_{0}^{2}$
. By Lemma 6.11 and Remark 6.12, applied to the Lie algebra
$\mathfrak{l}_{1}=\mathfrak{l}_{0}^{2}$
. By Lemma 6.11 and Remark 6.12, applied to the Lie algebra
![]() $\mathfrak{G}_{r,\mathbb{C}_{p}}$
and the set of ideals
$\mathfrak{G}_{r,\mathbb{C}_{p}}$
and the set of ideals
![]() $\{\mathfrak{l}_{1}\mathbb{B}_{r}\}\text{}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}$
, (22) implies that
$\{\mathfrak{l}_{1}\mathbb{B}_{r}\}\text{}_{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}$
, (22) implies that
![]() $\mathfrak{l}_{1}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})\subset \mathfrak{G}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE}}$
. Observe that the left-hand side of the last equation is stable under
$\mathfrak{l}_{1}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r,\mathbb{C}_{p}})\subset \mathfrak{G}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE}}$
. Observe that the left-hand side of the last equation is stable under
![]() $\operatorname{Ad}(\unicode[STIX]{x1D6FE})$
, so we can write
$\operatorname{Ad}(\unicode[STIX]{x1D6FE})$
, so we can write
The same argument as in the end of the proof of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Theorem 6.2] shows that the extension of scalars to
![]() $\mathbb{C}_{p}$
in (23) is unnecessary, up to restricting the ideal
$\mathbb{C}_{p}$
in (23) is unnecessary, up to restricting the ideal
![]() $\mathfrak{l}_{1}$
. This amounts essentially to consider the inclusion
$\mathfrak{l}_{1}$
. This amounts essentially to consider the inclusion
![]() $\mathfrak{l}_{1}\cdot \mathbb{B}_{r,\mathbb{C}_{p}}\subset \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC}}$
modulo an ideal
$\mathfrak{l}_{1}\cdot \mathbb{B}_{r,\mathbb{C}_{p}}\subset \mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FC}}$
modulo an ideal
![]() $\mathfrak{a}$
of
$\mathfrak{a}$
of
![]() $\mathbb{I}_{r,0}$
, for every root
$\mathbb{I}_{r,0}$
, for every root
![]() $\unicode[STIX]{x1D6FC}$
, and rewrite it in terms of well-chosen
$\unicode[STIX]{x1D6FC}$
, and rewrite it in terms of well-chosen
![]() $\mathbb{Q}_{p}$
-bases for the
$\mathbb{Q}_{p}$
-bases for the
![]() $\mathbb{Q}_{p}$
-structures of the two sides. The projective limit over
$\mathbb{Q}_{p}$
-structures of the two sides. The projective limit over
![]() $\mathfrak{a}$
then gives the inclusion
$\mathfrak{a}$
then gives the inclusion
![]() $\mathfrak{l}_{1}\cdot \mathbb{B}_{r}\subset \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
. For
$\mathfrak{l}_{1}\cdot \mathbb{B}_{r}\subset \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
. For
![]() $\mathfrak{l}=\mathfrak{l}_{1}^{2}$
, Lemma 6.11 and Corollary 6.12 give
$\mathfrak{l}=\mathfrak{l}_{1}^{2}$
, Lemma 6.11 and Corollary 6.12 give
By definition, we have
![]() $\mathfrak{l}=\mathfrak{l}_{1}^{2}=\mathfrak{l}_{0}^{4}=\left(\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\mathfrak{l}^{\unicode[STIX]{x1D6FC}}\right)^{4}$
. For every
$\mathfrak{l}=\mathfrak{l}_{1}^{2}=\mathfrak{l}_{0}^{4}=\left(\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\mathfrak{l}^{\unicode[STIX]{x1D6FC}}\right)^{4}$
. For every
![]() $\unicode[STIX]{x1D6FC}$
the ideal
$\unicode[STIX]{x1D6FC}$
the ideal
![]() $\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
provided by Lemma 8.2 is independent of
$\mathfrak{l}^{\unicode[STIX]{x1D6FC}}$
provided by Lemma 8.2 is independent of
![]() $r$
, so
$r$
, so
![]() $\mathfrak{l}$
is also independent of
$\mathfrak{l}$
is also independent of
![]() $r$
. This concludes the proof of Theorem 8.1.◻
$r$
. This concludes the proof of Theorem 8.1.◻
Definition 8.4. We call Galois level of
![]() $\unicode[STIX]{x1D703}$
and denote by
$\unicode[STIX]{x1D703}$
and denote by
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}$
the largest ideal of
$\mathfrak{l}_{\unicode[STIX]{x1D703}}$
the largest ideal of
![]() $\mathbb{I}_{0}$
satisfying the inclusion (19).
$\mathbb{I}_{0}$
satisfying the inclusion (19).
8.1 The Galois level of ordinary families
We explain how, for an ordinary family of
![]() $\operatorname{GSp}_{4}$
-eigenforms, we can use our arguments to prove a stronger result than Theorem 8.1. Let
$\operatorname{GSp}_{4}$
-eigenforms, we can use our arguments to prove a stronger result than Theorem 8.1. Let
![]() $M$
be a positive integer. Let
$M$
be a positive integer. Let
![]() $\mathbb{T}^{\operatorname{ord}}$
be a local component of the big ordinary cuspidal Hecke algebra of level
$\mathbb{T}^{\operatorname{ord}}$
be a local component of the big ordinary cuspidal Hecke algebra of level
![]() $\unicode[STIX]{x1D6E4}_{1}(M)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
for
$\unicode[STIX]{x1D6E4}_{1}(M)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
for
![]() $\operatorname{GSp}_{4}$
; it is a finite and flat
$\operatorname{GSp}_{4}$
; it is a finite and flat
![]() $\unicode[STIX]{x1D6EC}_{2}$
-algebra. With the terminology of §4 we consider
$\unicode[STIX]{x1D6EC}_{2}$
-algebra. With the terminology of §4 we consider
![]() $\mathbb{T}^{\operatorname{ord}}$
as the genus
$\mathbb{T}^{\operatorname{ord}}$
as the genus
![]() $2$
,
$2$
,
![]() $0$
-adapted Hecke algebra of the given level. Suppose that the residual representation
$0$
-adapted Hecke algebra of the given level. Suppose that the residual representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}^{\operatorname{ord}}}$
associated with
$\overline{\unicode[STIX]{x1D70C}}_{\mathbb{T}^{\operatorname{ord}}}$
associated with
![]() $\mathbb{T}^{\operatorname{ord}}$
is absolutely irreducible and of
$\mathbb{T}^{\operatorname{ord}}$
is absolutely irreducible and of
![]() $\operatorname{Sym}^{3}$
type in the sense of Definition 3.11. Let
$\operatorname{Sym}^{3}$
type in the sense of Definition 3.11. Let
![]() $\unicode[STIX]{x1D703}:\mathbb{T}^{\operatorname{ord}}\rightarrow \mathbb{I}^{\circ }$
be a family, i.e. the morphism of finite
$\unicode[STIX]{x1D703}:\mathbb{T}^{\operatorname{ord}}\rightarrow \mathbb{I}^{\circ }$
be a family, i.e. the morphism of finite
![]() $\unicode[STIX]{x1D6EC}_{2}$
algebras describing an irreducible component of
$\unicode[STIX]{x1D6EC}_{2}$
algebras describing an irreducible component of
![]() $\mathbb{T}^{\operatorname{ord}}$
. By taking
$\mathbb{T}^{\operatorname{ord}}$
. By taking
![]() $h=0$
and
$h=0$
and
![]() $r_{h}=1$
in the construction in §4 we obtain
$r_{h}=1$
in the construction in §4 we obtain
![]() $\mathbb{T}_{h}=\mathbb{T}^{\operatorname{ord}}$
. Note that all of our arguments and constructions are valid for this algebra; none of them relied on the fact that the slope of the family was positive.
$\mathbb{T}_{h}=\mathbb{T}^{\operatorname{ord}}$
. Note that all of our arguments and constructions are valid for this algebra; none of them relied on the fact that the slope of the family was positive.
We keep all the notation we introduced for the family
![]() $\unicode[STIX]{x1D703}$
. Let
$\unicode[STIX]{x1D703}$
. Let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the Galois representation associated with
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the Galois representation associated with
![]() $\unicode[STIX]{x1D703}$
. Suppose that
$\unicode[STIX]{x1D703}$
. Suppose that
![]() $\unicode[STIX]{x1D70C}$
is
$\unicode[STIX]{x1D70C}$
is
![]() $\mathbb{Z}_{p}$
-regular in the sense of Definition 3.10. Then we have the following.
$\mathbb{Z}_{p}$
-regular in the sense of Definition 3.10. Then we have the following.
Theorem 8.5. There exists a non-zero ideal
![]() $\mathfrak{l}$
of
$\mathfrak{l}$
of
![]() $\mathbb{I}_{0}^{\circ }$
and an element
$\mathbb{I}_{0}^{\circ }$
and an element
![]() $g$
of
$g$
of
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
such that
$\operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
such that
The main difference with respect to the proof of Theorem 8.1 is that relative Sen theory is not necessary anymore, because the exponential of the Sen operator defined in §7.4 is replaced by an element provided by the ordinarity of
![]() $\unicode[STIX]{x1D70C}$
. This is the reason why we do not need the Lie-theoretic constructions and we obtain a group-theoretic result. Note that this also makes the inversion of
$\unicode[STIX]{x1D70C}$
. This is the reason why we do not need the Lie-theoretic constructions and we obtain a group-theoretic result. Note that this also makes the inversion of
![]() $p$
unnecessary. Theorem 8.5 is an analogue of [Reference LangLan16, Theorem 2.4], which deals with ordinary families of
$p$
unnecessary. Theorem 8.5 is an analogue of [Reference LangLan16, Theorem 2.4], which deals with ordinary families of
![]() $\operatorname{GL}_{2}$
-eigenforms, and a generalization to the case where
$\operatorname{GL}_{2}$
-eigenforms, and a generalization to the case where
![]() $\mathbb{I}^{\circ }\neq \unicode[STIX]{x1D6EC}_{2}$
of [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, Theorem 4.8] for
$\mathbb{I}^{\circ }\neq \unicode[STIX]{x1D6EC}_{2}$
of [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15, Theorem 4.8] for
![]() $n=2$
and families of residual symmetric cube type.
$n=2$
and families of residual symmetric cube type.
We only sketch the proof of the theorem, pointing out the differences with respect to that of Theorem 8.1.
Proof. Let
![]() $u=1+p$
, let
$u=1+p$
, let
![]() $\unicode[STIX]{x1D712}$
be the
$\unicode[STIX]{x1D712}$
be the
![]() $p$
-adic cyclotomic character and, for
$p$
-adic cyclotomic character and, for
![]() $\unicode[STIX]{x1D70E}\in \mathbb{I}_{0}^{\circ ,\times }$
, let
$\unicode[STIX]{x1D70E}\in \mathbb{I}_{0}^{\circ ,\times }$
, let
![]() $\operatorname{ur}(\unicode[STIX]{x1D70E}):G_{\mathbb{Q}_{p}}\rightarrow \mathbb{I}_{0}^{\circ ,\times }$
be the unramified character sending a lift of the Frobenius automorphism to
$\operatorname{ur}(\unicode[STIX]{x1D70E}):G_{\mathbb{Q}_{p}}\rightarrow \mathbb{I}_{0}^{\circ ,\times }$
be the unramified character sending a lift of the Frobenius automorphism to
![]() $\unicode[STIX]{x1D70E}$
. By Hida theory, the ordinarity of
$\unicode[STIX]{x1D70E}$
. By Hida theory, the ordinarity of
![]() $\unicode[STIX]{x1D703}$
implies the ordinarity of the Galois representation
$\unicode[STIX]{x1D703}$
implies the ordinarity of the Galois representation
![]() $\unicode[STIX]{x1D70C}$
, in the sense that the restriction of
$\unicode[STIX]{x1D70C}$
, in the sense that the restriction of
![]() $\unicode[STIX]{x1D70C}$
to a decomposition group at
$\unicode[STIX]{x1D70C}$
to a decomposition group at
![]() $p$
is a conjugate of an upper triangular representation with diagonal entries given by
$p$
is a conjugate of an upper triangular representation with diagonal entries given by
for some
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}\in \mathbb{I}_{0}^{\circ ,\times }$
. Consider a conjugate of
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}\in \mathbb{I}_{0}^{\circ ,\times }$
. Consider a conjugate of
![]() $\unicode[STIX]{x1D70C}$
that has the form displayed above. Up to conjugation by an upper triangular matrix, we can suppose that
$\unicode[STIX]{x1D70C}$
that has the form displayed above. Up to conjugation by an upper triangular matrix, we can suppose that
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}$
contains a diagonal
$\operatorname{Im}\unicode[STIX]{x1D70C}$
contains a diagonal
![]() $\mathbb{Z}_{p}$
-regular element. By Proposition 6.3, we can further replace the representation with a conjugate by a diagonal matrix such that
$\mathbb{Z}_{p}$
-regular element. By Proposition 6.3, we can further replace the representation with a conjugate by a diagonal matrix such that
![]() $\unicode[STIX]{x1D70C}(H_{0})\subset \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
. This is true because the basis we start with in the proof of Proposition 6.3 is replaced by a collinear one.
$\unicode[STIX]{x1D70C}(H_{0})\subset \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ })$
. This is true because the basis we start with in the proof of Proposition 6.3 is replaced by a collinear one.
We work from now on with the last one of the conjugates of the original
![]() $\unicode[STIX]{x1D70C}$
mentioned in the previous paragraph; this choice gives the element
$\unicode[STIX]{x1D70C}$
mentioned in the previous paragraph; this choice gives the element
![]() $g$
appearing in Theorem 8.5. It is clear from the form of
$g$
appearing in Theorem 8.5. It is clear from the form of
![]() $\unicode[STIX]{x1D70C}$
that there exists an element
$\unicode[STIX]{x1D70C}$
that there exists an element
![]() $\unicode[STIX]{x1D70E}$
in the inertia subgroup at
$\unicode[STIX]{x1D70E}$
in the inertia subgroup at
![]() $p$
such that
$p$
such that
![]() $\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})=C_{T_{1},T_{2}}$
, where
$\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D70E})=C_{T_{1},T_{2}}$
, where
![]() $C_{T_{1},T_{2}}$
is the matrix defined in §7.4. Hence,
$C_{T_{1},T_{2}}$
is the matrix defined in §7.4. Hence,
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}$
is stable under
$\operatorname{Im}\unicode[STIX]{x1D70C}$
is stable under
![]() $\operatorname{Ad}C_{T_{1},T_{2}}$
. The same argument as in Lemma 8.3, with the nilpotent algebra
$\operatorname{Ad}C_{T_{1},T_{2}}$
. The same argument as in Lemma 8.3, with the nilpotent algebra
![]() $\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}$
replaced by the unipotent subgroup
$\mathfrak{U}_{r,\mathbb{C}_{p}}^{\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FC}}$
replaced by the unipotent subgroup
![]() $U^{\unicode[STIX]{x1D6FC}}(\operatorname{Im}\unicode[STIX]{x1D70C})$
and the extension of rings
$U^{\unicode[STIX]{x1D6FC}}(\operatorname{Im}\unicode[STIX]{x1D70C})$
and the extension of rings
![]() $B_{r}\subset \mathbb{B}_{r}$
replaced by
$B_{r}\subset \mathbb{B}_{r}$
replaced by
![]() $\unicode[STIX]{x1D6EC}_{2}\subset \mathbb{I}_{0}^{\circ }$
, gives
$\unicode[STIX]{x1D6EC}_{2}\subset \mathbb{I}_{0}^{\circ }$
, gives
![]() $U^{\unicode[STIX]{x1D6FC}}(\operatorname{Im}\unicode[STIX]{x1D70C})$
a structure of
$U^{\unicode[STIX]{x1D6FC}}(\operatorname{Im}\unicode[STIX]{x1D70C})$
a structure of
![]() $\unicode[STIX]{x1D6EC}_{2}$
-module for every root
$\unicode[STIX]{x1D6EC}_{2}$
-module for every root
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $\operatorname{Sp}_{4}$
. By Proposition 6.14,
$\operatorname{Sp}_{4}$
. By Proposition 6.14,
![]() $U^{\unicode[STIX]{x1D6FC}}(\operatorname{Im}\unicode[STIX]{x1D70C})$
contains a basis of a
$U^{\unicode[STIX]{x1D6FC}}(\operatorname{Im}\unicode[STIX]{x1D70C})$
contains a basis of a
![]() $\unicode[STIX]{x1D6EC}_{2}$
-lattice in
$\unicode[STIX]{x1D6EC}_{2}$
-lattice in
![]() $\mathbb{I}_{0}^{\circ }$
for every
$\mathbb{I}_{0}^{\circ }$
for every
![]() $\unicode[STIX]{x1D6FC}$
. Hence, by Lemma 6.6,
$\unicode[STIX]{x1D6FC}$
. Hence, by Lemma 6.6,
![]() $U^{\unicode[STIX]{x1D6FC}}(\operatorname{Im}\unicode[STIX]{x1D70C})$
contains a non-zero ideal of
$U^{\unicode[STIX]{x1D6FC}}(\operatorname{Im}\unicode[STIX]{x1D70C})$
contains a non-zero ideal of
![]() $\mathbb{I}_{0}^{\circ }$
for every
$\mathbb{I}_{0}^{\circ }$
for every
![]() $\unicode[STIX]{x1D6FC}$
. By Lemma 6.11 the group
$\unicode[STIX]{x1D6FC}$
. By Lemma 6.11 the group
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}$
contains a non-trivial congruence subgroup of
$\operatorname{Im}\unicode[STIX]{x1D70C}$
contains a non-trivial congruence subgroup of
![]() $\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ })$
.◻
$\operatorname{Sp}_{4}(\mathbb{I}_{0}^{\circ })$
.◻
9 The symmetric cube morphisms of Hecke algebras
Let
![]() $\operatorname{Sym}^{3}:\operatorname{GL}_{2}\rightarrow \operatorname{GSp}_{4}$
be the morphism of group schemes over
$\operatorname{Sym}^{3}:\operatorname{GL}_{2}\rightarrow \operatorname{GSp}_{4}$
be the morphism of group schemes over
![]() $\mathbb{Z}$
defined by the symmetric cube representation of
$\mathbb{Z}$
defined by the symmetric cube representation of
![]() $\operatorname{GL}_{2}$
. If
$\operatorname{GL}_{2}$
. If
![]() $R$
is a ring, we still denote by
$R$
is a ring, we still denote by
![]() $\operatorname{Sym}^{3}$
the morphism
$\operatorname{Sym}^{3}$
the morphism
![]() $\operatorname{GL}_{2}(R)\rightarrow \operatorname{GSp}_{4}(R)$
induced by the morphism of group schemes. For every representation
$\operatorname{GL}_{2}(R)\rightarrow \operatorname{GSp}_{4}(R)$
induced by the morphism of group schemes. For every representation
![]() $\unicode[STIX]{x1D70C}$
of a group with values in
$\unicode[STIX]{x1D70C}$
of a group with values in
![]() $\operatorname{GL}_{2}(R)$
, we set
$\operatorname{GL}_{2}(R)$
, we set
![]() $\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}=\operatorname{Sym}^{3}\circ \,\,\unicode[STIX]{x1D70C}$
.
$\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}=\operatorname{Sym}^{3}\circ \,\,\unicode[STIX]{x1D70C}$
.
Kim and Shahidi [Reference Kim and ShahidiKS02, Theorem B] proved the existence of a Langlands functoriality transfer from
![]() $\operatorname{GL}_{2}$
to
$\operatorname{GL}_{2}$
to
![]() $\operatorname{GL}_{4}$
associated with
$\operatorname{GL}_{4}$
associated with
![]() $\operatorname{Sym}^{3}:\operatorname{GL}_{2}(\mathbb{C})\rightarrow \operatorname{GL}_{4}(\mathbb{C})$
. Thanks to an unpublished result by Jacquet, Piatetski-Shapiro and Shalika [Reference Kim and ShahidiKS02, Theorem 9.1], this transfer descends to
$\operatorname{Sym}^{3}:\operatorname{GL}_{2}(\mathbb{C})\rightarrow \operatorname{GL}_{4}(\mathbb{C})$
. Thanks to an unpublished result by Jacquet, Piatetski-Shapiro and Shalika [Reference Kim and ShahidiKS02, Theorem 9.1], this transfer descends to
![]() $\operatorname{GSp}_{4}$
. If
$\operatorname{GSp}_{4}$
. If
![]() $\unicode[STIX]{x1D70B}$
is an automorphic representation of
$\unicode[STIX]{x1D70B}$
is an automorphic representation of
![]() $\operatorname{GL}_{2}$
, then the automorphic representation
$\operatorname{GL}_{2}$
, then the automorphic representation
![]() $\unicode[STIX]{x1D6F1}=\operatorname{Sym}^{3}\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D6F1}=\operatorname{Sym}^{3}\unicode[STIX]{x1D70B}$
of
![]() $\operatorname{GSp}_{4}$
given by the above construction is globally generic. In particular, it does not correspond to a holomorphic modular form for
$\operatorname{GSp}_{4}$
given by the above construction is globally generic. In particular, it does not correspond to a holomorphic modular form for
![]() $\operatorname{GSp}_{4}$
. However, Ramakrishnan and Shahidi showed that, when
$\operatorname{GSp}_{4}$
. However, Ramakrishnan and Shahidi showed that, when
![]() $\unicode[STIX]{x1D70B}$
is associated with a modular form, the component at infinity
$\unicode[STIX]{x1D70B}$
is associated with a modular form, the component at infinity
![]() $\unicode[STIX]{x1D6F1}_{\infty }$
of
$\unicode[STIX]{x1D6F1}_{\infty }$
of
![]() $\unicode[STIX]{x1D6F1}$
can be replaced by a holomorphic representation
$\unicode[STIX]{x1D6F1}$
can be replaced by a holomorphic representation
![]() $\unicode[STIX]{x1D6F1}_{\infty }^{\operatorname{hol}}$
such that
$\unicode[STIX]{x1D6F1}_{\infty }^{\operatorname{hol}}$
such that
![]() $\unicode[STIX]{x1D6F1}_{f}\otimes \unicode[STIX]{x1D6F1}_{\infty }^{\operatorname{hol}}$
belongs to the
$\unicode[STIX]{x1D6F1}_{f}\otimes \unicode[STIX]{x1D6F1}_{\infty }^{\operatorname{hol}}$
belongs to the
![]() $L$
-packet of
$L$
-packet of
![]() $\unicode[STIX]{x1D6F1}$
. This is the content of [Reference Ramakrishnan and ShahidiRS07, Theorem A
$\unicode[STIX]{x1D6F1}$
. This is the content of [Reference Ramakrishnan and ShahidiRS07, Theorem A
![]() $^{\prime }$
], that we recall below. Note that in [Reference Ramakrishnan and ShahidiRS07, Theorem A
$^{\prime }$
], that we recall below. Note that in [Reference Ramakrishnan and ShahidiRS07, Theorem A
![]() $^{\prime }$
], the theorem is stated only for
$^{\prime }$
], the theorem is stated only for
![]() $\unicode[STIX]{x1D70B}$
associated with a form
$\unicode[STIX]{x1D70B}$
associated with a form
![]() $f$
of level
$f$
of level
![]() $\unicode[STIX]{x1D6E4}_{0}(N)$
and even weight
$\unicode[STIX]{x1D6E4}_{0}(N)$
and even weight
![]() $k\geqslant 2$
, but Ramakrishnan pointed out that the proof also works when
$k\geqslant 2$
, but Ramakrishnan pointed out that the proof also works when
![]() $f$
has level
$f$
has level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
and arbitrary weight
$\unicode[STIX]{x1D6E4}_{1}(N)$
and arbitrary weight
![]() $k\geqslant 2$
.
$k\geqslant 2$
.
Let
![]() $\unicode[STIX]{x1D70B}$
be the automorphic representation of
$\unicode[STIX]{x1D70B}$
be the automorphic representation of
![]() $\operatorname{GL}_{2}(\mathbb{A}_{\mathbb{Q}})$
associated with a cuspidal, non-CM eigenform
$\operatorname{GL}_{2}(\mathbb{A}_{\mathbb{Q}})$
associated with a cuspidal, non-CM eigenform
![]() $f$
of weight
$f$
of weight
![]() $k\geqslant 2$
and level
$k\geqslant 2$
and level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
for some
$\unicode[STIX]{x1D6E4}_{1}(N)$
for some
![]() $N\geqslant 1$
. Let
$N\geqslant 1$
. Let
![]() $p$
be a prime not dividing
$p$
be a prime not dividing
![]() $N$
and let
$N$
and let
![]() $\unicode[STIX]{x1D70C}_{f,p}$
be the
$\unicode[STIX]{x1D70C}_{f,p}$
be the
![]() $p$
-adic Galois representation attached to
$p$
-adic Galois representation attached to
![]() $f$
.
$f$
.
If
![]() $K$
is a compact open subgroup of
$K$
is a compact open subgroup of
![]() $\operatorname{GSp}_{4}(\widehat{\mathbb{Z}})$
, we call the level of
$\operatorname{GSp}_{4}(\widehat{\mathbb{Z}})$
, we call the level of
![]() $K$
the smallest integer
$K$
the smallest integer
![]() $M$
such that
$M$
such that
![]() $K$
contains the principal congruence subgroup of
$K$
contains the principal congruence subgroup of
![]() $\operatorname{GSp}_{4}(\widehat{\mathbb{Z}})$
of level
$\operatorname{GSp}_{4}(\widehat{\mathbb{Z}})$
of level
![]() $M$
. Given an automorphic representation
$M$
. Given an automorphic representation
![]() $\unicode[STIX]{x1D6F1}$
of
$\unicode[STIX]{x1D6F1}$
of
![]() $\operatorname{GSp}_{4}(\mathbb{A}_{\mathbb{Q}})$
, we call the level of
$\operatorname{GSp}_{4}(\mathbb{A}_{\mathbb{Q}})$
, we call the level of
![]() $\unicode[STIX]{x1D6F1}$
the smallest integer
$\unicode[STIX]{x1D6F1}$
the smallest integer
![]() $M$
such that the finite component of
$M$
such that the finite component of
![]() $\unicode[STIX]{x1D6F1}$
admits an invariant vector by a compact open subgroup of
$\unicode[STIX]{x1D6F1}$
admits an invariant vector by a compact open subgroup of
![]() $\operatorname{GSp}_{4}(\widehat{\mathbb{Z}})$
of level
$\operatorname{GSp}_{4}(\widehat{\mathbb{Z}})$
of level
![]() $M$
.
$M$
.
Theorem 9.1 (See [Reference Ramakrishnan and ShahidiRS07, Theorem A
 $^{\prime }$
]).
$^{\prime }$
]).
There exists a cuspidal automorphic representation
![]() $\unicode[STIX]{x1D6F1}^{\operatorname{hol}}=\bigotimes _{v}\unicode[STIX]{x1D6F1}_{v}^{\operatorname{hol}}$
of
$\unicode[STIX]{x1D6F1}^{\operatorname{hol}}=\bigotimes _{v}\unicode[STIX]{x1D6F1}_{v}^{\operatorname{hol}}$
of
![]() $\operatorname{GSp}_{4}(\mathbb{A}_{\mathbb{Q}})$
, satisfying:
$\operatorname{GSp}_{4}(\mathbb{A}_{\mathbb{Q}})$
, satisfying:
(i)
 $\unicode[STIX]{x1D6F1}_{\infty }^{\operatorname{hol}}$
is in the holomorphic discrete series;
$\unicode[STIX]{x1D6F1}_{\infty }^{\operatorname{hol}}$
is in the holomorphic discrete series;(ii)
 $L(s,\unicode[STIX]{x1D6F1}^{\operatorname{hol}})=L(s,\unicode[STIX]{x1D70B},\operatorname{Sym}^{3})$
;
$L(s,\unicode[STIX]{x1D6F1}^{\operatorname{hol}})=L(s,\unicode[STIX]{x1D70B},\operatorname{Sym}^{3})$
;(iii)
 $\unicode[STIX]{x1D6F1}^{\operatorname{hol}}$
is unramified at primes not dividing
$\unicode[STIX]{x1D6F1}^{\operatorname{hol}}$
is unramified at primes not dividing
 $N$
;
$N$
;(iv)
 $\unicode[STIX]{x1D6F1}^{\operatorname{hol}}$
admits an invariant vector by a compact open subgroup
$\unicode[STIX]{x1D6F1}^{\operatorname{hol}}$
admits an invariant vector by a compact open subgroup
 $K$
of
$K$
of
 $\operatorname{GSp}_{4}(\mathbb{A}_{\mathbb{Q}})$
of level
$\operatorname{GSp}_{4}(\mathbb{A}_{\mathbb{Q}})$
of level
 $N(\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p})$
.
$N(\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p})$
.
A simple computation of Hodge–Tate weights gives the following corollary.
Corollary 9.2. Let
![]() $f$
be a cuspidal, non-CM
$f$
be a cuspidal, non-CM
![]() $\operatorname{GL}_{2}$
-eigenform of weight
$\operatorname{GL}_{2}$
-eigenform of weight
![]() $k\geqslant 2$
. For every prime
$k\geqslant 2$
. For every prime
![]() $\ell$
, let
$\ell$
, let
![]() $\unicode[STIX]{x1D70C}_{f,\ell }$
be the
$\unicode[STIX]{x1D70C}_{f,\ell }$
be the
![]() $\ell$
-adic Galois representation associated with
$\ell$
-adic Galois representation associated with
![]() $f$
. There exists a cuspidal
$f$
. There exists a cuspidal
![]() $\operatorname{GSp}_{4}$
-eigenform
$\operatorname{GSp}_{4}$
-eigenform
![]() $F$
of weight
$F$
of weight
![]() $(2k-1,k+1)$
with associated
$(2k-1,k+1)$
with associated
![]() $\ell$
-adic Galois representation
$\ell$
-adic Galois representation
![]() $\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,\ell }$
for every prime
$\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,\ell }$
for every prime
![]() $\ell$
. For every prime
$\ell$
. For every prime
![]() $p$
not dividing
$p$
not dividing
![]() $N$
, the level of
$N$
, the level of
![]() $F$
is a divisor of the prime-to-
$F$
is a divisor of the prime-to-
![]() $p$
conductor of
$p$
conductor of
![]() $\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
.
$\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
.
We denote by
![]() $\operatorname{Sym}^{3}f$
the cuspidal Siegel eigenform given by the corollary. Let
$\operatorname{Sym}^{3}f$
the cuspidal Siegel eigenform given by the corollary. Let
![]() $N(f)$
and
$N(f)$
and
![]() $N(\operatorname{Sym}^{3}f)$
be the levels of
$N(\operatorname{Sym}^{3}f)$
be the levels of
![]() $f$
and
$f$
and
![]() $\operatorname{Sym}^{3}f$
, respectively. We give an upper bound for
$\operatorname{Sym}^{3}f$
, respectively. We give an upper bound for
![]() $N(\operatorname{Sym}^{3}f)$
in terms of
$N(\operatorname{Sym}^{3}f)$
in terms of
![]() $N(f)$
. Let
$N(f)$
. Let
![]() $N(f)=\prod _{i=1}^{d}\ell _{i}^{a_{i}}$
be the decomposition of
$N(f)=\prod _{i=1}^{d}\ell _{i}^{a_{i}}$
be the decomposition of
![]() $N(f)$
in powers of distinct prime factors. For
$N(f)$
in powers of distinct prime factors. For
![]() $i\in \{1,2,\ldots ,d\}$
set
$i\in \{1,2,\ldots ,d\}$
set
We define
![]() $M(f)=\prod _{i=1}^{d}\ell _{i}^{a_{i}^{\prime }}$
.
$M(f)=\prod _{i=1}^{d}\ell _{i}^{a_{i}^{\prime }}$
.
Corollary 9.3. We have
![]() $N(\operatorname{Sym}^{3}f)\mid M(f)$
. In particular,
$N(\operatorname{Sym}^{3}f)\mid M(f)$
. In particular,
![]() $N(\operatorname{Sym}^{3}f)\mid N(f)^{3}$
.
$N(\operatorname{Sym}^{3}f)\mid N(f)^{3}$
.
Proof. At places where the automorphic representation
![]() $\unicode[STIX]{x1D70B}$
giving rise to
$\unicode[STIX]{x1D70B}$
giving rise to
![]() $f$
is Steinberg and Iwahori-spherical, we look at regular unipotent elements in the image of an inertia subgroup at
$f$
is Steinberg and Iwahori-spherical, we look at regular unipotent elements in the image of an inertia subgroup at
![]() $p$
to check that the symmetric cube of
$p$
to check that the symmetric cube of
![]() $\unicode[STIX]{x1D70B}$
is also Iwahori-spherical. At the other places, we give a bound on the conductor of the local Galois representation via Livné’s formula [Reference LivnéLiv89, Proposition 1.1] and apply Theorem 9.1(iv).◻
$\unicode[STIX]{x1D70B}$
is also Iwahori-spherical. At the other places, we give a bound on the conductor of the local Galois representation via Livné’s formula [Reference LivnéLiv89, Proposition 1.1] and apply Theorem 9.1(iv).◻
Borrowing the terminology of [Reference LudwigLud14, §4.3], we say that
![]() $\unicode[STIX]{x1D6E4}_{1}^{(1)}(N)$
and
$\unicode[STIX]{x1D6E4}_{1}^{(1)}(N)$
and
![]() $\unicode[STIX]{x1D6E4}_{1}^{(2)}(N^{3})$
are compatible levels for the symmetric cube transfer for all
$\unicode[STIX]{x1D6E4}_{1}^{(2)}(N^{3})$
are compatible levels for the symmetric cube transfer for all
![]() $N\in \mathbb{N}$
.
$N\in \mathbb{N}$
.
9.1 Constructing the morphisms of Hecke algebras
As usual, we fix an integer
![]() $N\geqslant 1$
and a prime
$N\geqslant 1$
and a prime
![]() $p$
not dividing
$p$
not dividing
![]() $N$
. We work with the abstract Hecke algebras
$N$
. We work with the abstract Hecke algebras
![]() ${\mathcal{H}}_{1}^{N}$
,
${\mathcal{H}}_{1}^{N}$
,
![]() ${\mathcal{H}}_{2}^{N}$
spherical outside
${\mathcal{H}}_{2}^{N}$
spherical outside
![]() $N$
and Iwahoric dilating at
$N$
and Iwahoric dilating at
![]() $p$
. Let
$p$
. Let
![]() $M=N^{3}$
. If
$M=N^{3}$
. If
![]() $f$
is a non-CM
$f$
is a non-CM
![]() $\operatorname{GL}_{2}$
-eigenform of level
$\operatorname{GL}_{2}$
-eigenform of level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
, we denote by
$\unicode[STIX]{x1D6E4}_{1}(N)$
, we denote by
![]() $\operatorname{Sym}^{3}f$
the classical, cuspidal
$\operatorname{Sym}^{3}f$
the classical, cuspidal
![]() $\operatorname{GSp}_{4}$
-eigenform of level
$\operatorname{GSp}_{4}$
-eigenform of level
![]() $\unicode[STIX]{x1D6E4}_{1}(M)$
given by Corollary 9.2. In the following, we define some morphisms of Hecke algebras that allow to recover the system of Hecke eigenvalues of the
$\unicode[STIX]{x1D6E4}_{1}(M)$
given by Corollary 9.2. In the following, we define some morphisms of Hecke algebras that allow to recover the system of Hecke eigenvalues of the
![]() $p$
-stabilizations of
$p$
-stabilizations of
![]() $\operatorname{Sym}^{3}f$
in terms of that of a
$\operatorname{Sym}^{3}f$
in terms of that of a
![]() $p$
-stabilization of
$p$
-stabilization of
![]() $f$
. If
$f$
. If
![]() $\unicode[STIX]{x1D712}$
is a system of Hecke eigenvalues, we write
$\unicode[STIX]{x1D712}$
is a system of Hecke eigenvalues, we write
![]() $\unicode[STIX]{x1D712}_{\ell }$
for its local component at the prime
$\unicode[STIX]{x1D712}_{\ell }$
for its local component at the prime
![]() $\ell$
.
$\ell$
.
Definition 9.4. For every prime
![]() $\ell \nmid Np$
, let
$\ell \nmid Np$
, let
be the morphism defined by
 $$\begin{eqnarray}\displaystyle T_{\ell ,0}^{(2)} & \mapsto & \displaystyle (T_{\ell ,0}^{(1)})^{3},\nonumber\\ \displaystyle T_{\ell ,1}^{(2)} & \mapsto & \displaystyle -(T_{\ell ,1}^{(1)})^{6}+(4\ell -2)T_{\ell ,0}^{(1)}(T_{\ell ,1}^{(1)})^{4}+(6\ell -4\ell ^{2})(T_{\ell ,0}^{(1)})^{2}(T_{\ell ,1}^{(1)})^{2}-3\ell ^{2}(T_{\ell ,0}^{(1)})^{3},\nonumber\\ \displaystyle T_{\ell ,2}^{(2)} & \mapsto & \displaystyle (T_{\ell ,1}^{(1)})^{3}-2\ell T_{\ell ,1}^{(1)}T_{\ell ,0}^{(1)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{\ell ,0}^{(2)} & \mapsto & \displaystyle (T_{\ell ,0}^{(1)})^{3},\nonumber\\ \displaystyle T_{\ell ,1}^{(2)} & \mapsto & \displaystyle -(T_{\ell ,1}^{(1)})^{6}+(4\ell -2)T_{\ell ,0}^{(1)}(T_{\ell ,1}^{(1)})^{4}+(6\ell -4\ell ^{2})(T_{\ell ,0}^{(1)})^{2}(T_{\ell ,1}^{(1)})^{2}-3\ell ^{2}(T_{\ell ,0}^{(1)})^{3},\nonumber\\ \displaystyle T_{\ell ,2}^{(2)} & \mapsto & \displaystyle (T_{\ell ,1}^{(1)})^{3}-2\ell T_{\ell ,1}^{(1)}T_{\ell ,0}^{(1)}.\nonumber\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D706}^{Np}:{\mathcal{H}}_{2}^{Np}\rightarrow {\mathcal{H}}_{1}^{Np}$
be the morphism defined by
$\unicode[STIX]{x1D706}^{Np}:{\mathcal{H}}_{2}^{Np}\rightarrow {\mathcal{H}}_{1}^{Np}$
be the morphism defined by
![]() $\unicode[STIX]{x1D706}^{Np}=\bigotimes _{\ell \nmid Np}\unicode[STIX]{x1D706}_{\ell }$
.
$\unicode[STIX]{x1D706}^{Np}=\bigotimes _{\ell \nmid Np}\unicode[STIX]{x1D706}_{\ell }$
.
Definition 9.5. For
![]() $i\in \{1,2,\ldots ,8\}$
we define morphisms
$i\in \{1,2,\ldots ,8\}$
we define morphisms
For
![]() $i\in \{1,2,3,4\}$
, the morphism
$i\in \{1,2,3,4\}$
, the morphism
![]() $\unicode[STIX]{x1D706}_{i,p}$
is defined on a set of generators of
$\unicode[STIX]{x1D706}_{i,p}$
is defined on a set of generators of
![]() ${\mathcal{H}}(T_{2}(\mathbb{Q}_{p}),T_{2}(\mathbb{Z}_{p}))^{-}$
as follows:
${\mathcal{H}}(T_{2}(\mathbb{Q}_{p}),T_{2}(\mathbb{Z}_{p}))^{-}$
as follows:

For
![]() $i\in \{5,6,7,8\}$
, the morphism
$i\in \{5,6,7,8\}$
, the morphism
![]() $\unicode[STIX]{x1D706}_{i,p}:{\mathcal{H}}(T_{2}(\mathbb{Q}_{p}),T_{2}(\mathbb{Z}_{p}))\rightarrow {\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))$
is given by
$\unicode[STIX]{x1D706}_{i,p}:{\mathcal{H}}(T_{2}(\mathbb{Q}_{p}),T_{2}(\mathbb{Z}_{p}))\rightarrow {\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))$
is given by
where
![]() $\unicode[STIX]{x1D6FF}$
is the automorphism of
$\unicode[STIX]{x1D6FF}$
is the automorphism of
![]() ${\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))$
defined on a set of generators of the subalgebra
${\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))$
defined on a set of generators of the subalgebra
![]() ${\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))^{-}$
by
${\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))^{-}$
by
and extended in the unique way.
Let
![]() $f$
be as in the beginning of the section and let
$f$
be as in the beginning of the section and let
![]() $f^{\operatorname{st}}$
be one of its
$f^{\operatorname{st}}$
be one of its
![]() $p$
-stabilizations. Let
$p$
-stabilizations. Let
![]() $\unicode[STIX]{x1D712}_{1,p}:{\mathcal{H}}(\operatorname{GL}_{2}(\mathbb{Q}_{p}),\operatorname{GL}_{2}(\mathbb{Z}_{p}))\rightarrow \overline{\mathbb{Q}}_{p}$
and
$\unicode[STIX]{x1D712}_{1,p}:{\mathcal{H}}(\operatorname{GL}_{2}(\mathbb{Q}_{p}),\operatorname{GL}_{2}(\mathbb{Z}_{p}))\rightarrow \overline{\mathbb{Q}}_{p}$
and
![]() $\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}:{\mathcal{H}}(\operatorname{GL}_{2}(\mathbb{Q}_{p}),I_{1,p})^{-}\rightarrow \overline{\mathbb{Q}}_{p}$
be the systems of Hecke eigenvalues at
$\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}:{\mathcal{H}}(\operatorname{GL}_{2}(\mathbb{Q}_{p}),I_{1,p})^{-}\rightarrow \overline{\mathbb{Q}}_{p}$
be the systems of Hecke eigenvalues at
![]() $p$
of
$p$
of
![]() $f$
and
$f$
and
![]() $f^{\operatorname{st}}$
, respectively. Note that
$f^{\operatorname{st}}$
, respectively. Note that
![]() $\unicode[STIX]{x1D712}_{1,p}$
is the restriction of
$\unicode[STIX]{x1D712}_{1,p}$
is the restriction of
![]() $\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}$
to the abstract spherical Hecke algebra at
$\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}$
to the abstract spherical Hecke algebra at
![]() $p$
.
$p$
.
Recall from §2.2 that for
![]() $g=1,2$
there is an isomorphism of
$g=1,2$
there is an isomorphism of
![]() $\mathbb{Q}$
-algebras
$\mathbb{Q}$
-algebras
Let
![]() $\unicode[STIX]{x1D704}_{T_{2}}^{I_{2,p}}$
be its inverse. Then
$\unicode[STIX]{x1D704}_{T_{2}}^{I_{2,p}}$
be its inverse. Then
![]() $\unicode[STIX]{x1D712}_{g}^{\operatorname{st}}\circ \,\unicode[STIX]{x1D704}_{T_{g}}^{I_{g,p}}$
is a character
$\unicode[STIX]{x1D712}_{g}^{\operatorname{st}}\circ \,\unicode[STIX]{x1D704}_{T_{g}}^{I_{g,p}}$
is a character
![]() ${\mathcal{H}}(T_{g}(\mathbb{Q}_{p}),T_{g}(\mathbb{Z}_{p}))^{-}\rightarrow \overline{\mathbb{Q}}_{p}$
, that can be extended uniquely to a character
${\mathcal{H}}(T_{g}(\mathbb{Q}_{p}),T_{g}(\mathbb{Z}_{p}))^{-}\rightarrow \overline{\mathbb{Q}}_{p}$
, that can be extended uniquely to a character
![]() $(\unicode[STIX]{x1D712}_{g,p}^{\operatorname{st}}\circ \,\unicode[STIX]{x1D704}_{T_{g}}^{I_{g,p}})^{\operatorname{ext}}:{\mathcal{H}}(T_{g}(\mathbb{Q}_{p}),T_{g}(\mathbb{Z}_{p}))\rightarrow \overline{\mathbb{Q}}_{p}$
.
$(\unicode[STIX]{x1D712}_{g,p}^{\operatorname{st}}\circ \,\unicode[STIX]{x1D704}_{T_{g}}^{I_{g,p}})^{\operatorname{ext}}:{\mathcal{H}}(T_{g}(\mathbb{Q}_{p}),T_{g}(\mathbb{Z}_{p}))\rightarrow \overline{\mathbb{Q}}_{p}$
.
The morphism
![]() $\unicode[STIX]{x1D706}_{1,p}$
factors as
$\unicode[STIX]{x1D706}_{1,p}$
factors as
![]() $\unicode[STIX]{x1D704}_{1,p}^{-}\circ \,\unicode[STIX]{x1D706}_{1,p}^{-}$
for some morphism
$\unicode[STIX]{x1D704}_{1,p}^{-}\circ \,\unicode[STIX]{x1D706}_{1,p}^{-}$
for some morphism
and the natural inclusion
![]() $\unicode[STIX]{x1D704}_{g,p}^{-}:{\mathcal{H}}(T_{g}(\mathbb{Q}_{p}),T_{g}(\mathbb{Z}_{p}))^{-}\rightarrow {\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{p}),I_{g,p})$
.
$\unicode[STIX]{x1D704}_{g,p}^{-}:{\mathcal{H}}(T_{g}(\mathbb{Q}_{p}),T_{g}(\mathbb{Z}_{p}))^{-}\rightarrow {\mathcal{H}}(\operatorname{GSp}_{2g}(\mathbb{Q}_{p}),I_{g,p})$
.
Definition 9.6. We set
![]() $\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}^{Np}\otimes \unicode[STIX]{x1D706}_{1,p}^{-}$
.
$\unicode[STIX]{x1D706}_{1}=\unicode[STIX]{x1D706}^{Np}\otimes \unicode[STIX]{x1D706}_{1,p}^{-}$
.
Let
![]() $\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}:{\mathcal{H}}_{2}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the character defined by:
$\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}:{\mathcal{H}}_{2}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the character defined by:
(i)
 $\unicode[STIX]{x1D712}_{2,\ell }^{\operatorname{st},i}=\unicode[STIX]{x1D712}_{1,\ell }^{\operatorname{st}}\circ \,\unicode[STIX]{x1D706}_{i}$
for every prime
$\unicode[STIX]{x1D712}_{2,\ell }^{\operatorname{st},i}=\unicode[STIX]{x1D712}_{1,\ell }^{\operatorname{st}}\circ \,\unicode[STIX]{x1D706}_{i}$
for every prime
 $\ell \nmid Np$
;
$\ell \nmid Np$
;(ii)
 $\unicode[STIX]{x1D712}_{2,p}^{\operatorname{st},i}=(\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}\circ \,\unicode[STIX]{x1D704}_{I_{1,p}}^{T_{1}})^{\operatorname{ext}}\circ \,\unicode[STIX]{x1D706}_{i,p}\circ \,\unicode[STIX]{x1D704}_{T_{2}}^{I_{2,p}}$
.
$\unicode[STIX]{x1D712}_{2,p}^{\operatorname{st},i}=(\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}\circ \,\unicode[STIX]{x1D704}_{I_{1,p}}^{T_{1}})^{\operatorname{ext}}\circ \,\unicode[STIX]{x1D706}_{i,p}\circ \,\unicode[STIX]{x1D704}_{T_{2}}^{I_{2,p}}$
.
Proposition 9.7. For every
![]() $i\in \{1,2,\ldots ,8\}$
, the form
$i\in \{1,2,\ldots ,8\}$
, the form
![]() $\operatorname{Sym}^{3}f$
has a
$\operatorname{Sym}^{3}f$
has a
![]() $p$
-stabilization
$p$
-stabilization
![]() $(\operatorname{Sym}^{3}f)_{i}^{\operatorname{st}}$
with associated system of Hecke eigenvalues
$(\operatorname{Sym}^{3}f)_{i}^{\operatorname{st}}$
with associated system of Hecke eigenvalues
![]() $\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}$
. Conversely, if
$\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}$
. Conversely, if
![]() $(\operatorname{Sym}^{3}f)^{\operatorname{st}}$
is a
$(\operatorname{Sym}^{3}f)^{\operatorname{st}}$
is a
![]() $p$
-stabilization of
$p$
-stabilization of
![]() $\operatorname{Sym}^{3}f$
with associated system of Hecke eigenvalues
$\operatorname{Sym}^{3}f$
with associated system of Hecke eigenvalues
![]() $\unicode[STIX]{x1D712}_{2}^{\operatorname{st}}$
, then there exists
$\unicode[STIX]{x1D712}_{2}^{\operatorname{st}}$
, then there exists
![]() $i\in \{1,2,\ldots ,8\}$
such that
$i\in \{1,2,\ldots ,8\}$
such that
![]() $\unicode[STIX]{x1D712}_{2}^{\operatorname{st}}=\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}$
.
$\unicode[STIX]{x1D712}_{2}^{\operatorname{st}}=\unicode[STIX]{x1D712}_{2}^{\operatorname{st},i}$
.
Proof. In this proof, we leave the composition with the isomorphism
![]() $\unicode[STIX]{x1D704}_{I_{1,p}}^{T_{1}}$
and
$\unicode[STIX]{x1D704}_{I_{1,p}}^{T_{1}}$
and
![]() $\unicode[STIX]{x1D704}_{I_{2,p}}^{T_{2}}$
implicit and we consider
$\unicode[STIX]{x1D704}_{I_{2,p}}^{T_{2}}$
implicit and we consider
![]() $\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}$
and
$\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}$
and
![]() $\unicode[STIX]{x1D712}_{2,p}^{\operatorname{st}}$
as characters of
$\unicode[STIX]{x1D712}_{2,p}^{\operatorname{st}}$
as characters of
![]() ${\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))^{-}$
and
${\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))^{-}$
and
![]() ${\mathcal{H}}(T_{2}(\mathbb{Q}_{p}),T_{2}(\mathbb{Z}_{p}))^{-}$
, respectively, for notational ease. Let
${\mathcal{H}}(T_{2}(\mathbb{Q}_{p}),T_{2}(\mathbb{Z}_{p}))^{-}$
, respectively, for notational ease. Let
![]() $\unicode[STIX]{x1D70C}_{f,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
be the
$\unicode[STIX]{x1D70C}_{f,p}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
be the
![]() $p$
-adic Galois representation associated with
$p$
-adic Galois representation associated with
![]() $f$
, so that the
$f$
, so that the
![]() $p$
-adic Galois representation associated with
$p$
-adic Galois representation associated with
![]() $\operatorname{Sym}^{3}f$
is
$\operatorname{Sym}^{3}f$
is
![]() $\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
. Via
$\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
. Via
![]() $p$
-adic Hodge theory, we attach to
$p$
-adic Hodge theory, we attach to
![]() $\unicode[STIX]{x1D70C}_{f,p}$
a two-dimensional
$\unicode[STIX]{x1D70C}_{f,p}$
a two-dimensional
![]() $\overline{\mathbb{Q}}_{p}$
-vector space
$\overline{\mathbb{Q}}_{p}$
-vector space
![]() $\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p})$
endowed with a
$\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p})$
endowed with a
![]() $\overline{\mathbb{Q}}_{p}$
-linear Frobenius endomorphism
$\overline{\mathbb{Q}}_{p}$
-linear Frobenius endomorphism
![]() $\unicode[STIX]{x1D711}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p})$
satisfying
$\unicode[STIX]{x1D711}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p})$
satisfying
![]() $\det (1-X\unicode[STIX]{x1D711}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p}))=\unicode[STIX]{x1D712}_{1,p}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))$
.
$\det (1-X\unicode[STIX]{x1D711}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{f,p}))=\unicode[STIX]{x1D712}_{1,p}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))$
.
We use the notation of §2.2.1 for the elements of the Weyl groups of
![]() $\operatorname{GL}_{2}$
and
$\operatorname{GL}_{2}$
and
![]() $\operatorname{GSp}_{4}$
. Let
$\operatorname{GSp}_{4}$
. Let
![]() $\unicode[STIX]{x1D6FC}_{p}$
and
$\unicode[STIX]{x1D6FC}_{p}$
and
![]() $\unicode[STIX]{x1D6FD}_{p}$
be the two roots of
$\unicode[STIX]{x1D6FD}_{p}$
be the two roots of
![]() $\unicode[STIX]{x1D712}_{1,p}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))$
, ordered so that
$\unicode[STIX]{x1D712}_{1,p}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))$
, ordered so that
![]() $\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}(t_{p,1}^{(1)})=\unicode[STIX]{x1D6FC}_{p}$
and
$\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}(t_{p,1}^{(1)})=\unicode[STIX]{x1D6FC}_{p}$
and
![]() $\unicode[STIX]{x1D6FD}_{p}=\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}((t_{p,1}^{(1)})^{w})$
.
$\unicode[STIX]{x1D6FD}_{p}=\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}((t_{p,1}^{(1)})^{w})$
.
Let
![]() $\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p})$
be the four-dimensional
$\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p})$
be the four-dimensional
![]() $\overline{\mathbb{Q}}_{p}$
-vector space attached to
$\overline{\mathbb{Q}}_{p}$
-vector space attached to
![]() $\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p}$
by
$\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p}$
by
![]() $p$
-adic Hodge theory. Denote by
$p$
-adic Hodge theory. Denote by
![]() $\unicode[STIX]{x1D711}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p})$
the Frobenius endomorphism acting on
$\unicode[STIX]{x1D711}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p})$
the Frobenius endomorphism acting on
![]() $\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p})$
. It satisfies
$\mathbf{D}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p})$
. It satisfies
![]() $\det (1-X\unicode[STIX]{x1D711}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p}))=\unicode[STIX]{x1D712}_{2,p}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))$
by [Reference UrbanUrb05, Théorème 1]. The coefficients of
$\det (1-X\unicode[STIX]{x1D711}_{\operatorname{cris}}(\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p}))=\unicode[STIX]{x1D712}_{2,p}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))$
by [Reference UrbanUrb05, Théorème 1]. The coefficients of
![]() $P_{\operatorname{min}}(t_{p,2}^{(2)};X)$
belong to the spherical Hecke algebra at
$P_{\operatorname{min}}(t_{p,2}^{(2)};X)$
belong to the spherical Hecke algebra at
![]() $p$
, so we have
$p$
, so we have
![]() $\unicode[STIX]{x1D712}_{2,p}^{\operatorname{st}}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))=\unicode[STIX]{x1D712}_{2,p}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))$
. From the relation
$\unicode[STIX]{x1D712}_{2,p}^{\operatorname{st}}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))=\unicode[STIX]{x1D712}_{2,p}(P_{\operatorname{min}}(t_{p,2}^{(2)};X))$
. From the relation
![]() $\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p}=\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
and (4) we deduce that
$\unicode[STIX]{x1D70C}_{\operatorname{Sym}^{3}f,p}=\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{f,p}$
and (4) we deduce that
In particular, the sets of roots of the two sides must coincide. As
![]() $t_{\ell ,2}^{(2)}(t_{\ell ,2}^{(2)})^{w_{1}w_{2}}=(t_{\ell ,2}^{(2)})^{w_{1}}(t_{\ell ,2}^{(2)})^{w_{2}}$
we have eight possible choices. Four choices for the
$t_{\ell ,2}^{(2)}(t_{\ell ,2}^{(2)})^{w_{1}w_{2}}=(t_{\ell ,2}^{(2)})^{w_{1}}(t_{\ell ,2}^{(2)})^{w_{2}}$
we have eight possible choices. Four choices for the
![]() $4$
-tuple
$4$
-tuple
are
The other four choices are obtained by exchanging
![]() $\unicode[STIX]{x1D6FC}_{p}$
with
$\unicode[STIX]{x1D6FC}_{p}$
with
![]() $\unicode[STIX]{x1D6FD}_{p}$
in the above.
$\unicode[STIX]{x1D6FD}_{p}$
in the above.
By writing
![]() $\unicode[STIX]{x1D6FC}_{p}=\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}(t_{p,1}^{(1)})$
,
$\unicode[STIX]{x1D6FC}_{p}=\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}(t_{p,1}^{(1)})$
,
![]() $\unicode[STIX]{x1D6FD}_{p}=\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}((t_{p,1}^{(1)})^{w})$
and recalling the relations
$\unicode[STIX]{x1D6FD}_{p}=\unicode[STIX]{x1D712}_{1,p}^{\operatorname{st}}((t_{p,1}^{(1)})^{w})$
and recalling the relations
![]() $t_{p,1}^{(2)}=t_{p,2}^{(2)}(t_{p,2}^{(2)})^{w_{1}}$
and
$t_{p,1}^{(2)}=t_{p,2}^{(2)}(t_{p,2}^{(2)})^{w_{1}}$
and
![]() $t_{p,0}^{(2)}=t_{p,2}^{(2)}(t_{p,2}^{(2)})^{w_{1}w_{2}}$
, we find that the first four choices for the triple
$t_{p,0}^{(2)}=t_{p,2}^{(2)}(t_{p,2}^{(2)})^{w_{1}w_{2}}$
, we find that the first four choices for the triple
are
The four other choices are obtained by replacing
![]() $t_{p,0}^{(1)}$
and
$t_{p,0}^{(1)}$
and
![]() $t_{p,1}^{(1)}$
in the triples above by their images via the automorphism
$t_{p,1}^{(1)}$
in the triples above by their images via the automorphism
![]() $\unicode[STIX]{x1D6FF}$
of
$\unicode[STIX]{x1D6FF}$
of
![]() ${\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))$
defined by (25).
${\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))$
defined by (25).
Let
![]() $\unicode[STIX]{x1D706}_{p}:{\mathcal{H}}(T_{2}(\mathbb{Q}_{p}),T_{2}(\mathbb{Z}_{p}))^{-}\rightarrow {\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))$
be a morphism satisfying
$\unicode[STIX]{x1D706}_{p}:{\mathcal{H}}(T_{2}(\mathbb{Q}_{p}),T_{2}(\mathbb{Z}_{p}))^{-}\rightarrow {\mathcal{H}}(T_{1}(\mathbb{Q}_{p}),T_{1}(\mathbb{Z}_{p}))$
be a morphism satisfying
![]() $\unicode[STIX]{x1D712}_{2}^{\operatorname{st}}=(\unicode[STIX]{x1D712}_{1}^{\operatorname{st}})^{\operatorname{ext}}\circ \,\unicode[STIX]{x1D706}_{p}\circ \,\unicode[STIX]{x1D704}_{2,p}^{-}$
(recall that we leave the maps
$\unicode[STIX]{x1D712}_{2}^{\operatorname{st}}=(\unicode[STIX]{x1D712}_{1}^{\operatorname{st}})^{\operatorname{ext}}\circ \,\unicode[STIX]{x1D706}_{p}\circ \,\unicode[STIX]{x1D704}_{2,p}^{-}$
(recall that we leave the maps
![]() $\unicode[STIX]{x1D704}_{I_{g,p}}^{T_{g}}$
implicit). By the arguments of the previous paragraph, this happens if and only if the triple
$\unicode[STIX]{x1D704}_{I_{g,p}}^{T_{g}}$
implicit). By the arguments of the previous paragraph, this happens if and only if the triple
![]() $(\unicode[STIX]{x1D706}_{i,p}(t_{p,0}^{(2)}),\unicode[STIX]{x1D706}_{i,p}(t_{p,1}^{(2)}),\unicode[STIX]{x1D706}_{i,p}(t_{p,2}^{(2)}))$
coincides with one of the four listed in (26) or the four derived from those by applying
$(\unicode[STIX]{x1D706}_{i,p}(t_{p,0}^{(2)}),\unicode[STIX]{x1D706}_{i,p}(t_{p,1}^{(2)}),\unicode[STIX]{x1D706}_{i,p}(t_{p,2}^{(2)}))$
coincides with one of the four listed in (26) or the four derived from those by applying
![]() $\unicode[STIX]{x1D6FF}$
. A simple check shows that these triples correspond to the choices
$\unicode[STIX]{x1D6FF}$
. A simple check shows that these triples correspond to the choices
![]() $\unicode[STIX]{x1D706}_{p}=\unicode[STIX]{x1D706}_{i,p}$
for
$\unicode[STIX]{x1D706}_{p}=\unicode[STIX]{x1D706}_{i,p}$
for
![]() $i\in \{1,2,\ldots ,8\}$
.◻
$i\in \{1,2,\ldots ,8\}$
.◻
Let
![]() $f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}}$
be a
$f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}}$
be a
![]() $p$
-stabilization of a classical, cuspidal, non-CM
$p$
-stabilization of a classical, cuspidal, non-CM
![]() $\operatorname{GL}_{2}$
-eigenform
$\operatorname{GL}_{2}$
-eigenform
![]() $f$
. Let
$f$
. Let
![]() $h$
be the slope of
$h$
be the slope of
![]() $f$
. For
$f$
. For
![]() $i\in \{1,2,3,4\}$
, denote by
$i\in \{1,2,3,4\}$
, denote by
![]() $\operatorname{Sym}^{3}(f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}})_{i}$
the
$\operatorname{Sym}^{3}(f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}})_{i}$
the
![]() $\operatorname{GSp}_{4}$
-eigenform
$\operatorname{GSp}_{4}$
-eigenform
![]() $(\operatorname{Sym}^{3}f)_{i}^{\operatorname{st}}$
given by Proposition 9.7. The forms
$(\operatorname{Sym}^{3}f)_{i}^{\operatorname{st}}$
given by Proposition 9.7. The forms
![]() $(\operatorname{Sym}^{3}f)_{i}^{\operatorname{st}}$
with
$(\operatorname{Sym}^{3}f)_{i}^{\operatorname{st}}$
with
![]() $5\leqslant i\leqslant 8$
coincide with
$5\leqslant i\leqslant 8$
coincide with
![]() $(\operatorname{Sym}^{3}f_{\unicode[STIX]{x1D6FD}}^{\operatorname{st}})_{i}$
,
$(\operatorname{Sym}^{3}f_{\unicode[STIX]{x1D6FD}}^{\operatorname{st}})_{i}$
,
![]() $1\leqslant i\leqslant 4$
, where
$1\leqslant i\leqslant 4$
, where
![]() $f_{\unicode[STIX]{x1D6FD}}^{\operatorname{st}}$
is the
$f_{\unicode[STIX]{x1D6FD}}^{\operatorname{st}}$
is the
![]() $p$
-stabilization of
$p$
-stabilization of
![]() $f$
different from
$f$
different from
![]() $f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}}$
. Let
$f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}}$
. Let
![]() $k$
and
$k$
and
![]() $h$
be the weight and slope, respectively, of
$h$
be the weight and slope, respectively, of
![]() $f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}}$
. The following corollary is derived from Proposition 9.7 via some simple calculations.
$f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}}$
. The following corollary is derived from Proposition 9.7 via some simple calculations.
Corollary 9.8. The slopes of the forms
![]() $\operatorname{Sym}^{3}(f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}})_{i}$
, with
$\operatorname{Sym}^{3}(f_{\unicode[STIX]{x1D6FC}}^{\operatorname{st}})_{i}$
, with
![]() $1\leqslant i\leqslant 4$
, are
$1\leqslant i\leqslant 4$
, are
If
![]() $f^{\operatorname{st}}$
is a
$f^{\operatorname{st}}$
is a
![]() $p$
-old
$p$
-old
![]() $\operatorname{GL}_{2}$
-eigenform of level
$\operatorname{GL}_{2}$
-eigenform of level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
, we write
$\unicode[STIX]{x1D6E4}_{1}(N)\cap \unicode[STIX]{x1D6E4}_{0}(p)$
, we write
![]() $\unicode[STIX]{x1D712}_{2,f^{\operatorname{st}}}^{i}$
for the system of Hecke eigenvalues of
$\unicode[STIX]{x1D712}_{2,f^{\operatorname{st}}}^{i}$
for the system of Hecke eigenvalues of
![]() $\operatorname{Sym}^{3}(f^{\operatorname{st}})_{i}$
,
$\operatorname{Sym}^{3}(f^{\operatorname{st}})_{i}$
,
![]() $1\leqslant i\leqslant 4$
. For a
$1\leqslant i\leqslant 4$
. For a
![]() $\overline{\mathbb{Q}}_{p}$
-point
$\overline{\mathbb{Q}}_{p}$
-point
![]() $x$
of
$x$
of
![]() ${\mathcal{D}}_{2}^{M}$
let
${\mathcal{D}}_{2}^{M}$
let
![]() $\unicode[STIX]{x1D712}_{x}:{\mathcal{H}}_{2}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the system of Hecke eigenvalues associated with
$\unicode[STIX]{x1D712}_{x}:{\mathcal{H}}_{2}^{N}\rightarrow \overline{\mathbb{Q}}_{p}$
be the system of Hecke eigenvalues associated with
![]() $x$
. For
$x$
. For
![]() $1\leqslant i\leqslant 4$
, let
$1\leqslant i\leqslant 4$
, let
![]() $S_{i}^{\operatorname{Sym}^{3}}$
be the set of
$S_{i}^{\operatorname{Sym}^{3}}$
be the set of
![]() $\overline{\mathbb{Q}}_{p}$
-points
$\overline{\mathbb{Q}}_{p}$
-points
![]() $x$
of
$x$
of
![]() ${\mathcal{D}}_{2}^{M}$
defined by the condition
${\mathcal{D}}_{2}^{M}$
defined by the condition
By combining Corollary 9.8 with the fact that the slope is bounded on an affinoid domain, we obtain the following.
Corollary 9.9. If
![]() $i\neq 1$
, then the set
$i\neq 1$
, then the set
![]() $S_{i}^{\operatorname{Sym}^{3}}$
is discrete in
$S_{i}^{\operatorname{Sym}^{3}}$
is discrete in
![]() ${\mathcal{D}}_{2}^{M}$
.
${\mathcal{D}}_{2}^{M}$
.
Remark 9.10. As a consequence of Corollary 9.9, the only symmetric cube lifts that we can hope to interpolate
![]() $p$
-adically are those in the set
$p$
-adically are those in the set
![]() $S_{1}^{\operatorname{Sym}^{3}}$
.
$S_{1}^{\operatorname{Sym}^{3}}$
.
9.2 The symmetric cube morphism of eigenvarieties
We fix until the end of the paper a continuous representation
![]() $\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{F}}_{p})$
. We let
$\overline{\unicode[STIX]{x1D70C}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{F}}_{p})$
. We let
![]() ${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
be the union of the connected components of
${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
be the union of the connected components of
![]() ${\mathcal{D}}_{1}^{N}$
having
${\mathcal{D}}_{1}^{N}$
having
![]() $\overline{\unicode[STIX]{x1D70C}}$
as associated residual representation. From now on we replace
$\overline{\unicode[STIX]{x1D70C}}$
as associated residual representation. From now on we replace
![]() ${\mathcal{D}}_{1}^{N}$
implicitly with
${\mathcal{D}}_{1}^{N}$
implicitly with
![]() ${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
(that is, we write
${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
(that is, we write
![]() ${\mathcal{D}}_{1}^{N}$
for
${\mathcal{D}}_{1}^{N}$
for
![]() ${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
). The only purpose of this choice is to assure that the symmetric cube morphism of eigenvarieties of Proposition 9.11 is a closed immersion. We also replace implicitly
${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
). The only purpose of this choice is to assure that the symmetric cube morphism of eigenvarieties of Proposition 9.11 is a closed immersion. We also replace implicitly
![]() ${\mathcal{D}}_{2}^{M}$
with
${\mathcal{D}}_{2}^{M}$
with
![]() ${\mathcal{D}}_{2,\operatorname{Sym}^{3}\overline{\unicode[STIX]{x1D70C}}}^{M}$
, because the symmetric cube morphism from
${\mathcal{D}}_{2,\operatorname{Sym}^{3}\overline{\unicode[STIX]{x1D70C}}}^{M}$
, because the symmetric cube morphism from
![]() ${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
will land into this connected component of
${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
will land into this connected component of
![]() ${\mathcal{D}}_{2}^{M}$
.
${\mathcal{D}}_{2}^{M}$
.
There is a map
![]() $\operatorname{Sym}_{1}^{3}$
from the set of classical, non-CM,
$\operatorname{Sym}_{1}^{3}$
from the set of classical, non-CM,
![]() $p$
-old points of
$p$
-old points of
![]() ${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
to the set
${\mathcal{D}}_{1,\overline{\unicode[STIX]{x1D70C}}}^{N}$
to the set
![]() $S_{1}^{\operatorname{Sym}^{3}}$
of Corollary 9.9; it maps a point
$S_{1}^{\operatorname{Sym}^{3}}$
of Corollary 9.9; it maps a point
![]() $x$
corresponding to an eigenform
$x$
corresponding to an eigenform
![]() $f$
to the point of
$f$
to the point of
![]() $S_{1}^{\operatorname{Sym}^{3}}$
corresponding to
$S_{1}^{\operatorname{Sym}^{3}}$
corresponding to
![]() $(\operatorname{Sym}^{3}f_{x})_{1}^{\operatorname{st}}$
. As we are fixing the residual representation
$(\operatorname{Sym}^{3}f_{x})_{1}^{\operatorname{st}}$
. As we are fixing the residual representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
, the map
$\overline{\unicode[STIX]{x1D70C}}$
, the map
![]() $\operatorname{Sym}_{1}^{3}$
is injective. Indeed, one has
$\operatorname{Sym}_{1}^{3}$
is injective. Indeed, one has
![]() $\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}^{\prime }$
for
$\operatorname{Sym}^{3}\unicode[STIX]{x1D70C}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}^{\prime }$
for
![]() $\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}^{\prime }:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
if and only if
$\unicode[STIX]{x1D70C},\unicode[STIX]{x1D70C}^{\prime }:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
if and only if
![]() $\unicode[STIX]{x1D70C}$
is a twist of
$\unicode[STIX]{x1D70C}$
is a twist of
![]() $\unicode[STIX]{x1D70C}^{\prime }$
with a character of order
$\unicode[STIX]{x1D70C}^{\prime }$
with a character of order
![]() $3$
, but this can be checked to be incompatible with them having the same residual representation.
$3$
, but this can be checked to be incompatible with them having the same residual representation.
We remind the reader that we only work on the connected components of identity of the various weights spaces. The association
![]() $k\mapsto (2k-1,k+1)$
is interpolated by the morphism of rigid analytic spaces
$k\mapsto (2k-1,k+1)$
is interpolated by the morphism of rigid analytic spaces
Recall the morphism
![]() $\unicode[STIX]{x1D706}_{1}:{\mathcal{H}}_{2}^{N}\rightarrow {\mathcal{H}}_{1}^{N}$
of Definition 9.6. The following proposition gives a morphism of eigenvarieties that interpolates the map
$\unicode[STIX]{x1D706}_{1}:{\mathcal{H}}_{2}^{N}\rightarrow {\mathcal{H}}_{1}^{N}$
of Definition 9.6. The following proposition gives a morphism of eigenvarieties that interpolates the map
![]() $\operatorname{Sym}_{1}^{3}$
.
$\operatorname{Sym}_{1}^{3}$
.
Proposition 9.11 [Reference ContiCon16, Propositions 3.9.5-7 and Definition 3.9.8].
There exists a closed immersion
![]() $\unicode[STIX]{x1D709}:{\mathcal{D}}_{1}^{N,{\mathcal{G}}}\rightarrow {\mathcal{D}}_{2}^{M}$
of rigid analytic spaces over
$\unicode[STIX]{x1D709}:{\mathcal{D}}_{1}^{N,{\mathcal{G}}}\rightarrow {\mathcal{D}}_{2}^{M}$
of rigid analytic spaces over
![]() $\mathbb{Q}_{p}$
such that the following diagrams commute.
$\mathbb{Q}_{p}$
such that the following diagrams commute.

The proof of Proposition 9.11 presented in [Reference ContiCon16] relies on the results of [Reference Bellaïche and ChenevierBC09, §7.2.3]. One can give an alternative proof using [Reference HansenHan17, Theorem 5.1.6] instead.
Remark 9.12. Let
![]() $f$
be a classical, cuspidal, CM
$f$
be a classical, cuspidal, CM
![]() $\operatorname{GL}_{2}$
-eigenform of level
$\operatorname{GL}_{2}$
-eigenform of level
![]() $\unicode[STIX]{x1D6E4}_{1}(N)$
. As
$\unicode[STIX]{x1D6E4}_{1}(N)$
. As
![]() $f$
is CM, the
$f$
is CM, the
![]() $\operatorname{GSp}_{4}$
-eigenform
$\operatorname{GSp}_{4}$
-eigenform
![]() $\operatorname{Sym}^{3}f$
provided by Corollary 9.2 may not be cuspidal. Suppose that it is not. Let
$\operatorname{Sym}^{3}f$
provided by Corollary 9.2 may not be cuspidal. Suppose that it is not. Let
![]() $x$
be a point of
$x$
be a point of
![]() ${\mathcal{D}}_{1}^{N}$
corresponding to a positive slope
${\mathcal{D}}_{1}^{N}$
corresponding to a positive slope
![]() $p$
-stabilization of
$p$
-stabilization of
![]() $f$
. By [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Corollary 3.6],
$f$
. By [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Corollary 3.6],
![]() $x$
is a CM point of a non-CM component
$x$
is a CM point of a non-CM component
![]() $I$
of
$I$
of
![]() ${\mathcal{D}}_{1}^{N}$
. Then
${\mathcal{D}}_{1}^{N}$
. Then
![]() $\unicode[STIX]{x1D709}(x)$
belongs to the cuspidal eigenvariety
$\unicode[STIX]{x1D709}(x)$
belongs to the cuspidal eigenvariety
![]() ${\mathcal{D}}_{2}^{M}$
, but it is not cuspidal since
${\mathcal{D}}_{2}^{M}$
, but it is not cuspidal since
![]() $\operatorname{Sym}^{3}f$
is not. This means that
$\operatorname{Sym}^{3}f$
is not. This means that
![]() $\unicode[STIX]{x1D709}(x)$
is a non-cuspidal specialization of a cuspidal family of
$\unicode[STIX]{x1D709}(x)$
is a non-cuspidal specialization of a cuspidal family of
![]() $\operatorname{GSp}_{4}$
-eigenforms. Brasca and Rosso [Reference Brasca and RossoBR16] constructed an eigenvariety for
$\operatorname{GSp}_{4}$
-eigenforms. Brasca and Rosso [Reference Brasca and RossoBR16] constructed an eigenvariety for
![]() $\operatorname{GSp}_{4}$
parametrizing the systems of Hecke eigenvalues associated with the non-cuspidal overconvergent eigenforms and they glued it with
$\operatorname{GSp}_{4}$
parametrizing the systems of Hecke eigenvalues associated with the non-cuspidal overconvergent eigenforms and they glued it with
![]() ${\mathcal{D}}_{2}^{M}$
. It should be possible to show that a cuspidal and a non-cuspidal component of this glued eigenvariety cross at
${\mathcal{D}}_{2}^{M}$
. It should be possible to show that a cuspidal and a non-cuspidal component of this glued eigenvariety cross at
![]() $\unicode[STIX]{x1D709}(x)$
.
$\unicode[STIX]{x1D709}(x)$
.
10 The symmetric cube locus on the
 $\text{GSp}_{4}$
-eigenvariety
$\text{GSp}_{4}$
-eigenvariety
The goal of this section is to give two definitions (a Galois-theoretic one and an automorphic one) of a symmetric cube locus on the
![]() $\operatorname{GSp}_{4}$
-eigenvariety and to show that they coincide. This is the content of Theorem 10.1. The main ingredient of the proof is Theorem 3.8. To apply it, we assume from now on that the representation
$\operatorname{GSp}_{4}$
-eigenvariety and to show that they coincide. This is the content of Theorem 10.1. The main ingredient of the proof is Theorem 3.8. To apply it, we assume from now on that the representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
fixed in the beginning of §9.2 satisfies conditions
$\overline{\unicode[STIX]{x1D70C}}$
fixed in the beginning of §9.2 satisfies conditions
![]() $(\ast _{\overline{\unicode[STIX]{x1D70C}}})$
.
$(\ast _{\overline{\unicode[STIX]{x1D70C}}})$
.
In the following,
![]() $p$
is a prime number,
$p$
is a prime number,
![]() $N$
is a positive integer prime to
$N$
is a positive integer prime to
![]() $p$
and
$p$
and
![]() $M=N^{3}$
. Let
$M=N^{3}$
. Let
![]() $T_{1}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{D}}_{1}^{N})$
and
$T_{1}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{D}}_{1}^{N})$
and
![]() $T_{2}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{D}}_{2}^{M})$
be the pseudocharacters provided by Proposition 2.5. By an abuse of notation, if
$T_{2}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{D}}_{2}^{M})$
be the pseudocharacters provided by Proposition 2.5. By an abuse of notation, if
![]() ${\mathcal{V}}_{1}$
and
${\mathcal{V}}_{1}$
and
![]() ${\mathcal{V}}_{2}$
are subvarieties of
${\mathcal{V}}_{2}$
are subvarieties of
![]() ${\mathcal{D}}_{1}^{N}$
and
${\mathcal{D}}_{1}^{N}$
and
![]() ${\mathcal{D}}_{2}^{M}$
, respectively, we still write
${\mathcal{D}}_{2}^{M}$
, respectively, we still write
![]() $\unicode[STIX]{x1D713}_{1}:{\mathcal{H}}_{1}^{N}\rightarrow {\mathcal{O}}({\mathcal{V}}_{1})$
and
$\unicode[STIX]{x1D713}_{1}:{\mathcal{H}}_{1}^{N}\rightarrow {\mathcal{O}}({\mathcal{V}}_{1})$
and
![]() $\unicode[STIX]{x1D713}_{2}:{\mathcal{H}}_{2}^{N}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
for the compositions of
$\unicode[STIX]{x1D713}_{2}:{\mathcal{H}}_{2}^{N}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
for the compositions of
![]() $\unicode[STIX]{x1D713}_{1}$
and
$\unicode[STIX]{x1D713}_{1}$
and
![]() $\unicode[STIX]{x1D713}_{2}$
with the restrictions of analytic functions to
$\unicode[STIX]{x1D713}_{2}$
with the restrictions of analytic functions to
![]() ${\mathcal{V}}_{1}$
and
${\mathcal{V}}_{1}$
and
![]() ${\mathcal{V}}_{2}$
, respectively. We also write
${\mathcal{V}}_{2}$
, respectively. We also write
![]() $T_{{\mathcal{V}}_{1}}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{1})$
and
$T_{{\mathcal{V}}_{1}}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{1})$
and
![]() $T_{{\mathcal{V}}_{2}}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
for the compositions of
$T_{{\mathcal{V}}_{2}}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
for the compositions of
![]() $T_{1}$
and
$T_{1}$
and
![]() $T_{2}$
with the restrictions of analytic functions to
$T_{2}$
with the restrictions of analytic functions to
![]() ${\mathcal{V}}_{1}$
and
${\mathcal{V}}_{1}$
and
![]() ${\mathcal{V}}_{2}$
, respectively.
${\mathcal{V}}_{2}$
, respectively.
Theorem 10.1. Let
![]() ${\mathcal{V}}_{2}$
be a rigid analytic subvariety of
${\mathcal{V}}_{2}$
be a rigid analytic subvariety of
![]() ${\mathcal{D}}_{2}^{M}$
. Consider the following four conditions.
${\mathcal{D}}_{2}^{M}$
. Consider the following four conditions.
(1a) There exists a morphism of rings
 $\unicode[STIX]{x1D713}_{2}^{(1)}:{\mathcal{H}}_{1}^{Np}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
such that the following diagram commutes. (28)
$\unicode[STIX]{x1D713}_{2}^{(1)}:{\mathcal{H}}_{1}^{Np}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
such that the following diagram commutes. (28)
(1b) There exists a pseudocharacter
 $T_{{\mathcal{V}}_{2},1}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
of dimension two such that (29)
$T_{{\mathcal{V}}_{2},1}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
of dimension two such that (29) $$\begin{eqnarray}T_{{\mathcal{V}}_{2}}=\operatorname{Sym}^{3}T_{{\mathcal{V}}_{2},1}.\end{eqnarray}$$
$$\begin{eqnarray}T_{{\mathcal{V}}_{2}}=\operatorname{Sym}^{3}T_{{\mathcal{V}}_{2},1}.\end{eqnarray}$$
(2a) There exists a rigid analytic subvariety
 ${\mathcal{V}}_{1}$
of
${\mathcal{V}}_{1}$
of
 ${\mathcal{D}}_{1}^{N}$
and a morphism of rings
${\mathcal{D}}_{1}^{N}$
and a morphism of rings
 $\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
such that the following diagram commutes. (30)
$\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
such that the following diagram commutes. (30)
(2b) There exists a rigid analytic subvariety
 ${\mathcal{V}}_{1}$
of
${\mathcal{V}}_{1}$
of
 ${\mathcal{D}}_{1}^{N}$
and a morphism of rings
${\mathcal{D}}_{1}^{N}$
and a morphism of rings
 $\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
such that (31)
$\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
such that (31) $$\begin{eqnarray}T_{{\mathcal{V}}_{2}}=\operatorname{Sym}^{3}(\unicode[STIX]{x1D719}\circ \,T_{{\mathcal{V}}_{1}}).\end{eqnarray}$$
$$\begin{eqnarray}T_{{\mathcal{V}}_{2}}=\operatorname{Sym}^{3}(\unicode[STIX]{x1D719}\circ \,T_{{\mathcal{V}}_{1}}).\end{eqnarray}$$
Then:
(i) conditions (1a) and (1b) are equivalent;
(ii) conditions (2a) and (2b) are equivalent;
(iii) condition (2b) implies condition (1b);
(iv) when
 ${\mathcal{V}}_{2}$
is a point, the four conditions are equivalent.
${\mathcal{V}}_{2}$
is a point, the four conditions are equivalent.
Proof. We prove statements (i), (ii) and (iii) for an arbitrary rigid analytic subvariety
![]() ${\mathcal{V}}_{2}$
of
${\mathcal{V}}_{2}$
of
![]() ${\mathcal{D}}_{2}^{M}$
.
${\mathcal{D}}_{2}^{M}$
.
(1a)
![]() $\;\Longrightarrow \;$
(1b). Let
$\;\Longrightarrow \;$
(1b). Let
![]() $\unicode[STIX]{x1D713}_{2}^{(1)}:{\mathcal{H}}_{1}^{Np}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
be a morphism of rings making diagram (28) commute. By the argument in the proof of Proposition 9.7, the commutativity of diagram (28) gives an equality
$\unicode[STIX]{x1D713}_{2}^{(1)}:{\mathcal{H}}_{1}^{Np}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
be a morphism of rings making diagram (28) commute. By the argument in the proof of Proposition 9.7, the commutativity of diagram (28) gives an equality
Choose a character
![]() $\unicode[STIX]{x1D700}_{1}$
satisfying
$\unicode[STIX]{x1D700}_{1}$
satisfying
![]() $\unicode[STIX]{x1D700}_{1}^{6}=\unicode[STIX]{x1D700}$
. For every
$\unicode[STIX]{x1D700}_{1}^{6}=\unicode[STIX]{x1D700}$
. For every
![]() $\ell$
not dividing
$\ell$
not dividing
![]() $Np$
, let
$Np$
, let
![]() $P_{\ell }$
be a polynomial in
$P_{\ell }$
be a polynomial in
![]() ${\mathcal{H}}_{2}^{Np}[X]^{\deg =2}$
satisfying
${\mathcal{H}}_{2}^{Np}[X]^{\deg =2}$
satisfying
Such a polynomial exists thanks to (32) and to Remark 4.8, and it is clearly unique. The roots of
![]() $P_{\ell }$
differ from those of
$P_{\ell }$
differ from those of
![]() $\unicode[STIX]{x1D713}_{2}(P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X))$
by a factor equal to a cubic root of
$\unicode[STIX]{x1D713}_{2}(P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X))$
by a factor equal to a cubic root of
![]() $1$
. The map
$1$
. The map
is continuous with respect to the restriction of the profinite topology on
![]() $G_{\mathbb{Q}}$
. This follows from the fact that the maps
$G_{\mathbb{Q}}$
. This follows from the fact that the maps
and
are continuous on
![]() $\{\unicode[STIX]{x1D6FE}\operatorname{Frob}_{\ell }\unicode[STIX]{x1D6FE}^{-1}\}\text{}_{\ell \nmid Np;\,\unicode[STIX]{x1D6FE}\in G_{\mathbb{Q}}}$
. By Chebotarev’s theorem
$\{\unicode[STIX]{x1D6FE}\operatorname{Frob}_{\ell }\unicode[STIX]{x1D6FE}^{-1}\}\text{}_{\ell \nmid Np;\,\unicode[STIX]{x1D6FE}\in G_{\mathbb{Q}}}$
. By Chebotarev’s theorem
![]() $P$
can be extended to a continuous map
$P$
can be extended to a continuous map
![]() $P:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})[X]^{\deg =2}$
. Now define a map
$P:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})[X]^{\deg =2}$
. Now define a map
![]() $T_{{\mathcal{V}}_{2},1}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
by
$T_{{\mathcal{V}}_{2},1}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
by
![]() $T_{{\mathcal{V}}_{2},1}(g)=(P(g)(-1)P(g)(1))/2$
. We can check that
$T_{{\mathcal{V}}_{2},1}(g)=(P(g)(-1)P(g)(1))/2$
. We can check that
![]() $T_{{\mathcal{V}}_{2},1}$
is a pseudocharacter of dimension two. Its characteristic polynomial is
$T_{{\mathcal{V}}_{2},1}$
is a pseudocharacter of dimension two. Its characteristic polynomial is
![]() $P$
, so the fact that
$P$
, so the fact that
![]() $T_{{\mathcal{V}}_{2}}=\operatorname{Sym}^{3}T_{{\mathcal{V}}_{2},1}$
follows from (33).
$T_{{\mathcal{V}}_{2}}=\operatorname{Sym}^{3}T_{{\mathcal{V}}_{2},1}$
follows from (33).
(1b)
![]() $\;\Longrightarrow \;$
(1a). Suppose that there exists a pseudocharacter
$\;\Longrightarrow \;$
(1a). Suppose that there exists a pseudocharacter
![]() $T_{{\mathcal{V}}_{2},1}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}_{{\mathcal{V}}_{2}}$
such that
$T_{{\mathcal{V}}_{2},1}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}_{{\mathcal{V}}_{2}}$
such that
![]() $T_{{\mathcal{V}}_{2}}=\operatorname{Sym}^{3}T_{{\mathcal{V}}_{2},1}$
. Then
$T_{{\mathcal{V}}_{2}}=\operatorname{Sym}^{3}T_{{\mathcal{V}}_{2},1}$
. Then
![]() $P_{\operatorname{char}}(T_{{\mathcal{V}}_{2}})=\operatorname{Sym}^{3}P_{\operatorname{char}}(T_{{\mathcal{V}}_{2},1})$
. By evaluating the two polynomials at
$P_{\operatorname{char}}(T_{{\mathcal{V}}_{2}})=\operatorname{Sym}^{3}P_{\operatorname{char}}(T_{{\mathcal{V}}_{2},1})$
. By evaluating the two polynomials at
![]() $\operatorname{Frob}_{\ell }$
we obtain
$\operatorname{Frob}_{\ell }$
we obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{2}(P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X)) & = & \displaystyle P_{\operatorname{char}}(T_{{\mathcal{V}}_{2}})(\operatorname{Frob}_{\ell })=\operatorname{Sym}^{3}P_{\operatorname{char}}(T_{{\mathcal{V}}_{2},1})(\operatorname{Frob}_{\ell })\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Sym}^{3}\left(X^{2}-T_{{\mathcal{V}}_{2},1}(\operatorname{Frob}_{\ell })X+\frac{T_{{\mathcal{V}}_{2},1}(\operatorname{Frob}_{\ell })^{2}-T_{{\mathcal{V}}_{2},1}(\operatorname{Frob}_{\ell }^{2})}{2}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}_{2}(P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X)) & = & \displaystyle P_{\operatorname{char}}(T_{{\mathcal{V}}_{2}})(\operatorname{Frob}_{\ell })=\operatorname{Sym}^{3}P_{\operatorname{char}}(T_{{\mathcal{V}}_{2},1})(\operatorname{Frob}_{\ell })\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Sym}^{3}\left(X^{2}-T_{{\mathcal{V}}_{2},1}(\operatorname{Frob}_{\ell })X+\frac{T_{{\mathcal{V}}_{2},1}(\operatorname{Frob}_{\ell })^{2}-T_{{\mathcal{V}}_{2},1}(\operatorname{Frob}_{\ell }^{2})}{2}\right),\end{eqnarray}$$
where the first equality is given by Proposition 2.5 and the last one comes from a trivial calculation. Let
![]() $\unicode[STIX]{x1D713}_{2}^{(1)}:{\mathcal{H}}_{1}^{Np}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
be a morphism of rings satisfying
$\unicode[STIX]{x1D713}_{2}^{(1)}:{\mathcal{H}}_{1}^{Np}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
be a morphism of rings satisfying
for every
![]() $\ell \nmid Np$
. It is clear that such a morphism exists and is unique. Note that the right-hand side of (36) is
$\ell \nmid Np$
. It is clear that such a morphism exists and is unique. Note that the right-hand side of (36) is
![]() $\unicode[STIX]{x1D713}_{2}^{(1)}(P_{\operatorname{min}}(t_{\ell ,1}^{(1)};X))$
. Then (35) gives
$\unicode[STIX]{x1D713}_{2}^{(1)}(P_{\operatorname{min}}(t_{\ell ,1}^{(1)};X))$
. Then (35) gives
Exactly as in the proof of Proposition 9.7, by developing the two polynomials and comparing their coefficients we obtain that
![]() $\unicode[STIX]{x1D713}_{2}=\unicode[STIX]{x1D713}_{2}^{(1)}\circ \,\unicode[STIX]{x1D706}^{Np}$
. Hence
$\unicode[STIX]{x1D713}_{2}=\unicode[STIX]{x1D713}_{2}^{(1)}\circ \,\unicode[STIX]{x1D706}^{Np}$
. Hence
![]() $\unicode[STIX]{x1D713}_{2}^{(1)}$
fits into diagram (28).
$\unicode[STIX]{x1D713}_{2}^{(1)}$
fits into diagram (28).
(2a)
![]() $\;\Longleftrightarrow \;$
(2b). Let
$\;\Longleftrightarrow \;$
(2b). Let
![]() ${\mathcal{V}}_{1}$
be a subvariety of
${\mathcal{V}}_{1}$
be a subvariety of
![]() ${\mathcal{D}}_{1}^{N}$
and let
${\mathcal{D}}_{1}^{N}$
and let
![]() $\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
be a morphism of rings. We show that the couple
$\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
be a morphism of rings. We show that the couple
![]() $({\mathcal{V}}_{1},\unicode[STIX]{x1D719})$
satisfies condition (2a) if and only if it satisfies condition (2b). For
$({\mathcal{V}}_{1},\unicode[STIX]{x1D719})$
satisfies condition (2a) if and only if it satisfies condition (2b). For
![]() $g=1,2$
and every prime
$g=1,2$
and every prime
![]() $\ell \nmid Np$
Proposition 2.5 gives
$\ell \nmid Np$
Proposition 2.5 gives
The argument in the proof of Proposition 9.7 gives an equality
As the set
![]() $\{\unicode[STIX]{x1D6FE}\operatorname{Frob}_{\ell }\unicode[STIX]{x1D6FE}^{-1}\}\text{}_{\ell \nmid Np;\,\unicode[STIX]{x1D6FE}\in G_{\mathbb{Q}}}$
is dense in
$\{\unicode[STIX]{x1D6FE}\operatorname{Frob}_{\ell }\unicode[STIX]{x1D6FE}^{-1}\}\text{}_{\ell \nmid Np;\,\unicode[STIX]{x1D6FE}\in G_{\mathbb{Q}}}$
is dense in
![]() $G_{\mathbb{Q}}$
, the pseudocharacters
$G_{\mathbb{Q}}$
, the pseudocharacters
![]() $\operatorname{Sym}^{3}(\unicode[STIX]{x1D719}\circ \,T_{{\mathcal{V}}_{1}})$
and
$\operatorname{Sym}^{3}(\unicode[STIX]{x1D719}\circ \,T_{{\mathcal{V}}_{1}})$
and
![]() $T_{{\mathcal{V}}_{2}}$
coincide if and only if their characteristic polynomials coincide on
$T_{{\mathcal{V}}_{2}}$
coincide if and only if their characteristic polynomials coincide on
![]() $\operatorname{Frob}_{\ell }$
for every
$\operatorname{Frob}_{\ell }$
for every
![]() $\ell \nmid Np$
. By (37), the condition above is equivalent to
$\ell \nmid Np$
. By (37), the condition above is equivalent to
for every
![]() $\ell \nmid Np$
. Thanks to (38) the left-hand side can be rewritten as
$\ell \nmid Np$
. Thanks to (38) the left-hand side can be rewritten as
When
![]() $\ell$
varies over the primes not dividing
$\ell$
varies over the primes not dividing
![]() $Np$
the coefficients of the polynomials
$Np$
the coefficients of the polynomials
![]() $P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X)$
generate the Hecke algebra
$P_{\operatorname{min}}(t_{\ell ,2}^{(2)};X)$
generate the Hecke algebra
![]() ${\mathcal{H}}_{2}^{Np}$
. Hence, the equality of the right-hand sides of the last two equations holds if and only if
${\mathcal{H}}_{2}^{Np}$
. Hence, the equality of the right-hand sides of the last two equations holds if and only if
![]() $\unicode[STIX]{x1D719}\circ \,\unicode[STIX]{x1D713}_{1}\circ \,\unicode[STIX]{x1D706}^{Np}=\unicode[STIX]{x1D713}_{2}$
.
$\unicode[STIX]{x1D719}\circ \,\unicode[STIX]{x1D713}_{1}\circ \,\unicode[STIX]{x1D706}^{Np}=\unicode[STIX]{x1D713}_{2}$
.
(2b)
![]() $\;\Longrightarrow \;$
(1b). Suppose that condition (2b) is satisfied by some closed subvariety
$\;\Longrightarrow \;$
(1b). Suppose that condition (2b) is satisfied by some closed subvariety
![]() ${\mathcal{V}}_{1}$
of
${\mathcal{V}}_{1}$
of
![]() ${\mathcal{D}}_{1}^{N}$
and some morphism of rings
${\mathcal{D}}_{1}^{N}$
and some morphism of rings
![]() $\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
. Consider the pseudocharacter
$\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
. Consider the pseudocharacter
![]() $T_{{\mathcal{V}}_{2},1}=\unicode[STIX]{x1D719}\circ \,T_{{\mathcal{V}}_{1}}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
. Clearly
$T_{{\mathcal{V}}_{2},1}=\unicode[STIX]{x1D719}\circ \,T_{{\mathcal{V}}_{1}}:G_{\mathbb{Q}}\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
. Clearly
![]() $T_{{\mathcal{V}}_{2},1}$
satisfies condition (1b).
$T_{{\mathcal{V}}_{2},1}$
satisfies condition (1b).
It remains to prove that condition (1b)
![]() $\;\Longrightarrow \;$
condition (2b) when
$\;\Longrightarrow \;$
condition (2b) when
![]() ${\mathcal{V}}_{2}$
is a
${\mathcal{V}}_{2}$
is a
![]() $\overline{\mathbb{Q}}_{p}$
-point of
$\overline{\mathbb{Q}}_{p}$
-point of
![]() ${\mathcal{D}}_{2}^{M}$
. Here, we need to apply Theorem 3.8. Write
${\mathcal{D}}_{2}^{M}$
. Here, we need to apply Theorem 3.8. Write
![]() $x_{2}$
for the point
$x_{2}$
for the point
![]() ${\mathcal{V}}_{2}$
; the system of eigenvalues
${\mathcal{V}}_{2}$
; the system of eigenvalues
![]() $\unicode[STIX]{x1D713}_{x_{2}}$
is that of a classical
$\unicode[STIX]{x1D713}_{x_{2}}$
is that of a classical
![]() $\operatorname{GSp}_{4}$
-eigenform. By Remark 2.6(i)
$\operatorname{GSp}_{4}$
-eigenform. By Remark 2.6(i)
![]() $T_{x_{2}}$
is the pseudocharacter associated with a representation
$T_{x_{2}}$
is the pseudocharacter associated with a representation
![]() $\unicode[STIX]{x1D70C}_{x_{2}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\overline{\mathbb{Q}}_{p})$
. Let
$\unicode[STIX]{x1D70C}_{x_{2}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{4}(\overline{\mathbb{Q}}_{p})$
. Let
![]() $E$
be a finite extension of
$E$
be a finite extension of
![]() $\mathbb{Q}_{p}$
over which
$\mathbb{Q}_{p}$
over which
![]() $\unicode[STIX]{x1D70C}_{x_{2}}$
is defined. Suppose that
$\unicode[STIX]{x1D70C}_{x_{2}}$
is defined. Suppose that
![]() $x_{2}$
satisfies condition (1b). Let
$x_{2}$
satisfies condition (1b). Let
![]() $T_{x_{2},1}:G_{\mathbb{Q}}\rightarrow \overline{\mathbb{Q}}_{p}$
be a pseudocharacter such that
$T_{x_{2},1}:G_{\mathbb{Q}}\rightarrow \overline{\mathbb{Q}}_{p}$
be a pseudocharacter such that
![]() $T_{x_{2}}\cong \operatorname{Sym}^{3}T_{x_{2},1}$
. By Taylor’s theorem in [Reference TaylorTay91] there exists a representation
$T_{x_{2}}\cong \operatorname{Sym}^{3}T_{x_{2},1}$
. By Taylor’s theorem in [Reference TaylorTay91] there exists a representation
![]() $\unicode[STIX]{x1D70C}_{x_{2},1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
such that
$\unicode[STIX]{x1D70C}_{x_{2},1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{Q}}_{p})$
such that
![]() $T_{x_{2},1}=\operatorname{Tr}(\unicode[STIX]{x1D70C}_{x_{2},1})$
. From the definition of the symmetric cube of a pseudocharacter, we deduce that
$T_{x_{2},1}=\operatorname{Tr}(\unicode[STIX]{x1D70C}_{x_{2},1})$
. From the definition of the symmetric cube of a pseudocharacter, we deduce that
![]() $\unicode[STIX]{x1D70C}_{x_{2}}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{x_{2},1}$
. As
$\unicode[STIX]{x1D70C}_{x_{2}}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{x_{2},1}$
. As
![]() $\unicode[STIX]{x1D70C}_{x_{2}}$
is attached to an overconvergent
$\unicode[STIX]{x1D70C}_{x_{2}}$
is attached to an overconvergent
![]() $\operatorname{GSp}_{4}$
-eigenform, Theorem 3.8(ii) implies that
$\operatorname{GSp}_{4}$
-eigenform, Theorem 3.8(ii) implies that
![]() $\unicode[STIX]{x1D70C}_{x_{2},1}$
is the
$\unicode[STIX]{x1D70C}_{x_{2},1}$
is the
![]() $p$
-adic Galois representation attached to an overconvergent
$p$
-adic Galois representation attached to an overconvergent
![]() $\operatorname{GL}_{2}$
-eigenform
$\operatorname{GL}_{2}$
-eigenform
![]() $f$
. Such a form defines a point
$f$
. Such a form defines a point
![]() $x_{1}$
of the eigencurve
$x_{1}$
of the eigencurve
![]() ${\mathcal{D}}_{1}^{N}$
. Thus, the subvariety
${\mathcal{D}}_{1}^{N}$
. Thus, the subvariety
![]() ${\mathcal{V}}_{1}=x_{1}$
satisfies condition (2b).◻
${\mathcal{V}}_{1}=x_{1}$
satisfies condition (2b).◻
In light of Theorem 10.1, we give the following definitions.
Definition 10.2.
(i) We say that a subvariety
 ${\mathcal{V}}_{2}$
of
${\mathcal{V}}_{2}$
of
 ${\mathcal{D}}_{2}^{M}$
is of
${\mathcal{D}}_{2}^{M}$
is of
 $\operatorname{Sym}^{3}$
type if it satisfies the equivalent conditions (2a) and (2b) of Theorem 10.1.
$\operatorname{Sym}^{3}$
type if it satisfies the equivalent conditions (2a) and (2b) of Theorem 10.1.(ii) The
 $\operatorname{Sym}^{3}$
-locus of
$\operatorname{Sym}^{3}$
-locus of
 ${\mathcal{D}}_{2}^{M}$
is the set of points of
${\mathcal{D}}_{2}^{M}$
is the set of points of
 ${\mathcal{D}}_{2}^{M}$
of
${\mathcal{D}}_{2}^{M}$
of
 $\operatorname{Sym}^{3}$
type.
$\operatorname{Sym}^{3}$
type.
Recall the closed immersion
![]() $\unicode[STIX]{x1D704}:{\mathcal{W}}_{1}^{\circ }\rightarrow {\mathcal{W}}_{2}^{\circ }$
defined in §9.2. Let
$\unicode[STIX]{x1D704}:{\mathcal{W}}_{1}^{\circ }\rightarrow {\mathcal{W}}_{2}^{\circ }$
defined in §9.2. Let
![]() ${\mathcal{D}}_{2,\unicode[STIX]{x1D704}}^{M}$
be the one-dimensional subvariety of
${\mathcal{D}}_{2,\unicode[STIX]{x1D704}}^{M}$
be the one-dimensional subvariety of
![]() ${\mathcal{D}}_{2}^{M}$
fitting in the following Cartesian diagram.
${\mathcal{D}}_{2}^{M}$
fitting in the following Cartesian diagram.

The following lemma follows from a simple computation involving the generalized Hodge–Tate weights of a point of
![]() $\operatorname{Sym}^{3}$
type.
$\operatorname{Sym}^{3}$
type.
Lemma 10.3. The
![]() $\operatorname{Sym}^{3}$
-locus of
$\operatorname{Sym}^{3}$
-locus of
![]() ${\mathcal{D}}_{2}^{M}$
is contained in the one-dimensional subvariety
${\mathcal{D}}_{2}^{M}$
is contained in the one-dimensional subvariety
![]() ${\mathcal{D}}_{2,\unicode[STIX]{x1D704}}^{M}$
.
${\mathcal{D}}_{2,\unicode[STIX]{x1D704}}^{M}$
.
The
![]() $\operatorname{Sym}^{3}$
-locus of
$\operatorname{Sym}^{3}$
-locus of
![]() ${\mathcal{D}}_{2}^{M}$
admits a Hecke-theoretic definition thanks to condition (2b) of Theorem 10.1.
${\mathcal{D}}_{2}^{M}$
admits a Hecke-theoretic definition thanks to condition (2b) of Theorem 10.1.
We define an ideal
![]() ${\mathcal{I}}_{\operatorname{Sym}^{3}}$
of
${\mathcal{I}}_{\operatorname{Sym}^{3}}$
of
![]() ${\mathcal{O}}({\mathcal{D}}_{2}^{M})$
by
${\mathcal{O}}({\mathcal{D}}_{2}^{M})$
by
We denote by
![]() ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
the analytic Zariski subvariety of
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
the analytic Zariski subvariety of
![]() ${\mathcal{D}}_{2}^{M}$
defined as the zero locus of the ideal
${\mathcal{D}}_{2}^{M}$
defined as the zero locus of the ideal
![]() ${\mathcal{I}}_{\operatorname{Sym}^{3}}$
.
${\mathcal{I}}_{\operatorname{Sym}^{3}}$
.
Proposition 10.4.
(i) The
 $\operatorname{Sym}^{3}$
-locus of
$\operatorname{Sym}^{3}$
-locus of
 ${\mathcal{D}}_{2}^{M}$
is the set of points underlying
${\mathcal{D}}_{2}^{M}$
is the set of points underlying
 ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
.
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
.(ii) The variety
 ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
is of
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
is of
 $\operatorname{Sym}^{3}$
type.
$\operatorname{Sym}^{3}$
type.(iii) A rigid analytic subvariety
 ${\mathcal{V}}_{2}$
of
${\mathcal{V}}_{2}$
of
 ${\mathcal{D}}_{2}^{M}$
is of
${\mathcal{D}}_{2}^{M}$
is of
 $\operatorname{Sym}^{3}$
type if and only if it is a subvariety of
$\operatorname{Sym}^{3}$
type if and only if it is a subvariety of
 ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
.
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
.(iv) A rigid analytic subvariety
 ${\mathcal{V}}_{2}$
of
${\mathcal{V}}_{2}$
of
 ${\mathcal{D}}_{2}^{M}$
satisfies conditions (1a) and (1b) of Theorem 10.1 if and only if it is a subvariety of
${\mathcal{D}}_{2}^{M}$
satisfies conditions (1a) and (1b) of Theorem 10.1 if and only if it is a subvariety of
 ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
.
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
.
Proof. Statements (i) and (ii), together with the ‘if’ implications of statements (iii) and (iv), follow immediately from the definition of
![]() ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
. If
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
. If
![]() ${\mathcal{V}}_{2}$
satisfies condition (2a) of Theorem 10.1, then one has
${\mathcal{V}}_{2}$
satisfies condition (2a) of Theorem 10.1, then one has
![]() $\unicode[STIX]{x1D713}_{2}=\unicode[STIX]{x1D719}\circ \,\unicode[STIX]{x1D713}_{1}\circ \,\unicode[STIX]{x1D706}^{Np}$
for some
$\unicode[STIX]{x1D713}_{2}=\unicode[STIX]{x1D719}\circ \,\unicode[STIX]{x1D713}_{1}\circ \,\unicode[STIX]{x1D706}^{Np}$
for some
![]() $\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
, so
$\unicode[STIX]{x1D719}:{\mathcal{O}}({\mathcal{V}}_{1})\rightarrow {\mathcal{O}}({\mathcal{V}}_{2})$
, so
![]() $\unicode[STIX]{x1D713}_{2}$
must vanish on
$\unicode[STIX]{x1D713}_{2}$
must vanish on
![]() $\ker (\unicode[STIX]{x1D713}_{1}\circ \,\unicode[STIX]{x1D706}^{Np})$
, giving the ‘only if’ implication of statement (iii).
$\ker (\unicode[STIX]{x1D713}_{1}\circ \,\unicode[STIX]{x1D706}^{Np})$
, giving the ‘only if’ implication of statement (iii).
For the remaining direction of statement (iv), let
![]() ${\mathcal{V}}_{2}$
be a rigid analytic subvariety of
${\mathcal{V}}_{2}$
be a rigid analytic subvariety of
![]() ${\mathcal{D}}_{2}^{M}$
satisfying conditions (1a) and (1b) of Theorem 10.1. Let
${\mathcal{D}}_{2}^{M}$
satisfying conditions (1a) and (1b) of Theorem 10.1. Let
![]() $x_{2}$
by a point of
$x_{2}$
by a point of
![]() ${\mathcal{V}}_{2}$
. Then
${\mathcal{V}}_{2}$
. Then
![]() $x_{2}$
satisfies conditions (1a) and (1b). By Theorem 10.1,
$x_{2}$
satisfies conditions (1a) and (1b). By Theorem 10.1,
![]() $x_{2}$
also satisfies conditions (2a) and (2b), so it is a point of
$x_{2}$
also satisfies conditions (2a) and (2b), so it is a point of
![]() ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
. We conclude that
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
. We conclude that
![]() ${\mathcal{V}}_{2}$
is a subvariety of
${\mathcal{V}}_{2}$
is a subvariety of
![]() ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
.◻
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
.◻
Remark 10.5. By Proposition 10.4 the
![]() $\operatorname{Sym}^{3}$
-locus in
$\operatorname{Sym}^{3}$
-locus in
![]() ${\mathcal{D}}_{2}^{M}$
can be given the structure of a Zariski-closed rigid analytic subspace. From now on, we will always consider the
${\mathcal{D}}_{2}^{M}$
can be given the structure of a Zariski-closed rigid analytic subspace. From now on, we will always consider the
![]() $\operatorname{Sym}^{3}$
-locus as equipped with this structure and we will identify it with the subvariety
$\operatorname{Sym}^{3}$
-locus as equipped with this structure and we will identify it with the subvariety
![]() ${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
of
${\mathcal{D}}_{2,\operatorname{Sym}^{3}}^{M}$
of
![]() ${\mathcal{D}}_{2}^{M}$
.
${\mathcal{D}}_{2}^{M}$
.
Proposition 10.4(i) and Lemma 10.3 give the following.
Corollary 10.6. The
![]() $\operatorname{Sym}^{3}$
-locus intersects each irreducible component of
$\operatorname{Sym}^{3}$
-locus intersects each irreducible component of
![]() ${\mathcal{D}}_{2}^{M}$
in a proper analytic subvariety of dimension at most
${\mathcal{D}}_{2}^{M}$
in a proper analytic subvariety of dimension at most
![]() $1$
.
$1$
.
Propositions 10.4(iii) and (iv) allow us to improve the result of Theorem 10.1.
Corollary 10.7. For every rigid analytic subvariety
![]() ${\mathcal{V}}_{2}$
of
${\mathcal{V}}_{2}$
of
![]() ${\mathcal{D}}_{2}^{M}$
, conditions (1a), (1b), (2a) and (2b) of Theorem 10.1 are equivalent.
${\mathcal{D}}_{2}^{M}$
, conditions (1a), (1b), (2a) and (2b) of Theorem 10.1 are equivalent.
11 An automorphic description of the Galois level
11.1 The fortuitous
 $\operatorname{Sym}^{3}$
-congruence ideal of a finite slope family
$\operatorname{Sym}^{3}$
-congruence ideal of a finite slope family
Let
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}{\twoheadrightarrow}\mathbb{I}^{\circ }$
be a finite slope family and let
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}{\twoheadrightarrow}\mathbb{I}^{\circ }$
be a finite slope family and let
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the representation associated with
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
be the representation associated with
![]() $\unicode[STIX]{x1D703}$
in the previous section. Recall that
$\unicode[STIX]{x1D703}$
in the previous section. Recall that
![]() $\overline{\unicode[STIX]{x1D70C}}$
is absolutely irreducible by assumption. We also assume that
$\overline{\unicode[STIX]{x1D70C}}$
is absolutely irreducible by assumption. We also assume that
![]() $\unicode[STIX]{x1D70C}$
is
$\unicode[STIX]{x1D70C}$
is
![]() $\mathbb{Z}_{p}$
-regular and of residual
$\mathbb{Z}_{p}$
-regular and of residual
![]() $\operatorname{Sym}^{3}$
type, as in Definitions 3.10 and 3.11. In this section, we define a ‘fortuitous congruence ideal’ for the family
$\operatorname{Sym}^{3}$
type, as in Definitions 3.10 and 3.11. In this section, we define a ‘fortuitous congruence ideal’ for the family
![]() $\unicode[STIX]{x1D703}$
. It is the ideal describing the intersection of the
$\unicode[STIX]{x1D703}$
. It is the ideal describing the intersection of the
![]() $\operatorname{Sym}^{3}$
-locus of
$\operatorname{Sym}^{3}$
-locus of
![]() ${\mathcal{D}}_{2}^{M}$
with the family
${\mathcal{D}}_{2}^{M}$
with the family
![]() $\unicode[STIX]{x1D703}$
. Recall that the
$\unicode[STIX]{x1D703}$
. Recall that the
![]() $\operatorname{Sym}^{3}$
-locus is the zero locus of the ideal
$\operatorname{Sym}^{3}$
-locus is the zero locus of the ideal
![]() ${\mathcal{I}}_{\operatorname{Sym}^{3}}$
of
${\mathcal{I}}_{\operatorname{Sym}^{3}}$
of
![]() ${\mathcal{O}}({\mathcal{D}}_{2}^{M})^{\circ }$
defined in §10 and that
${\mathcal{O}}({\mathcal{D}}_{2}^{M})^{\circ }$
defined in §10 and that
![]() $r_{{\mathcal{D}}_{2,B_{h}}^{M,h}}:{\mathcal{O}}({\mathcal{D}}_{2}^{M})^{\circ }\rightarrow \mathbb{T}_{h}$
denotes the restriction of analytic functions.
$r_{{\mathcal{D}}_{2,B_{h}}^{M,h}}:{\mathcal{O}}({\mathcal{D}}_{2}^{M})^{\circ }\rightarrow \mathbb{T}_{h}$
denotes the restriction of analytic functions.
Definition 11.1. The fortuitous
![]() $\operatorname{Sym}^{3}$
-congruence ideal for the family
$\operatorname{Sym}^{3}$
-congruence ideal for the family
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
is the ideal of
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
is the ideal of
![]() $\mathbb{I}_{0}^{\circ }$
defined by
$\mathbb{I}_{0}^{\circ }$
defined by
In most cases, we will simply refer to
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
as the ‘congruence ideal’. The next proposition describes its main properties. Let
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
as the ‘congruence ideal’. The next proposition describes its main properties. Let
![]() $\mathfrak{I}$
be an ideal of
$\mathfrak{I}$
be an ideal of
![]() $\mathbb{I}^{\circ }$
and let
$\mathbb{I}^{\circ }$
and let
![]() $\mathfrak{I}_{\operatorname{Tr}}=\mathfrak{I}\cap \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. Let
$\mathfrak{I}_{\operatorname{Tr}}=\mathfrak{I}\cap \mathbb{I}_{\operatorname{Tr}}^{\circ }$
. Let
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{I}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{I}_{\operatorname{Tr}})$
be the reduction of
$\unicode[STIX]{x1D70C}_{\mathfrak{I}}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ }/\mathfrak{I}_{\operatorname{Tr}})$
be the reduction of
![]() $\unicode[STIX]{x1D70C}$
modulo
$\unicode[STIX]{x1D70C}$
modulo
![]() $\mathfrak{I}$
. If
$\mathfrak{I}$
. If
![]() $\unicode[STIX]{x1D703}_{1}:\mathbb{T}_{h,1}\rightarrow \mathbb{J}$
is a finite slope family of
$\unicode[STIX]{x1D703}_{1}:\mathbb{T}_{h,1}\rightarrow \mathbb{J}$
is a finite slope family of
![]() $\operatorname{GL}_{2}$
-eigenforms we denote by
$\operatorname{GL}_{2}$
-eigenforms we denote by
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}_{1}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{J})$
the associated Galois representation. For an ideal
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}_{1}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{J})$
the associated Galois representation. For an ideal
![]() ${\mathcal{J}}$
of
${\mathcal{J}}$
of
![]() $\mathbb{J}$
we let
$\mathbb{J}$
we let
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}_{1},{\mathcal{J}}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{J}/{\mathcal{J}})$
be the reduction of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}_{1},{\mathcal{J}}}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{J}/{\mathcal{J}})$
be the reduction of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}_{1}}$
modulo
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}_{1}}$
modulo
![]() ${\mathcal{J}}$
.
${\mathcal{J}}$
.
For an ideal
![]() $\mathfrak{I}$
of
$\mathfrak{I}$
of
![]() $\mathbb{I}_{0}^{\circ }$
we denote by
$\mathbb{I}_{0}^{\circ }$
we denote by
![]() $\unicode[STIX]{x1D70C}_{\mathfrak{I}}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{I})$
the reduction of
$\unicode[STIX]{x1D70C}_{\mathfrak{I}}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0}^{\circ }/\mathfrak{I})$
the reduction of
![]() $\unicode[STIX]{x1D70C}|_{H_{0}}$
modulo
$\unicode[STIX]{x1D70C}|_{H_{0}}$
modulo
![]() $\mathfrak{I}$
. We give the following characterization of
$\mathfrak{I}$
. We give the following characterization of
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
.
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
.
Lemma 11.2. Let
![]() $P_{0}$
be a prime ideal of
$P_{0}$
be a prime ideal of
![]() $\mathbb{I}_{0}^{\circ }$
. The following are equivalent:
$\mathbb{I}_{0}^{\circ }$
. The following are equivalent:
(i)
 $P_{0}\supset \mathfrak{c}_{\unicode[STIX]{x1D703}}$
;
$P_{0}\supset \mathfrak{c}_{\unicode[STIX]{x1D703}}$
;(ii) there exists a finite extension
 $\mathbb{I}^{\prime }$
of
$\mathbb{I}^{\prime }$
of
 $\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
and a representation
$\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
and a representation
 $\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ },1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{I}^{\prime })$
such that
$\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ },1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{I}^{\prime })$
such that
 $\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ },1}$
over
$\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ },1}$
over
 $\mathbb{I}^{\prime }$
;
$\mathbb{I}^{\prime }$
;(iii) for one prime
 $P$
of
$P$
of
 $\mathbb{I}_{\operatorname{Tr}}^{\circ }$
lying above
$\mathbb{I}_{\operatorname{Tr}}^{\circ }$
lying above
 $P_{0}$
, there exists a finite extension
$P_{0}$
, there exists a finite extension
 $\mathfrak{I}^{\prime }$
of
$\mathfrak{I}^{\prime }$
of
 $\mathbb{I}_{\operatorname{Tr}}^{\circ }/P$
and a representation
$\mathbb{I}_{\operatorname{Tr}}^{\circ }/P$
and a representation
 $\unicode[STIX]{x1D70C}_{P,1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{I}^{\prime })$
such that
$\unicode[STIX]{x1D70C}_{P,1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\mathbb{I}^{\prime })$
such that
 $\unicode[STIX]{x1D70C}_{P}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{P,1}$
over
$\unicode[STIX]{x1D70C}_{P}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{P,1}$
over
 $\mathbb{I}^{\prime }$
;
$\mathbb{I}^{\prime }$
;(iv) there exists a representation
 $\unicode[STIX]{x1D70C}_{P_{0},1}:H_{0}\rightarrow \operatorname{GL}_{2}(\mathbb{I}_{0}^{\circ }/\mathfrak{I})$
such that
$\unicode[STIX]{x1D70C}_{P_{0},1}:H_{0}\rightarrow \operatorname{GL}_{2}(\mathbb{I}_{0}^{\circ }/\mathfrak{I})$
such that
 $\unicode[STIX]{x1D70C}_{P_{0}}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{P_{0},1}$
over
$\unicode[STIX]{x1D70C}_{P_{0}}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{P_{0},1}$
over
 $\mathbb{I}_{0}^{\circ }/\mathfrak{I}$
.
$\mathbb{I}_{0}^{\circ }/\mathfrak{I}$
.
Note that we did not specify the image in the weight space of the admissible subdomain of
![]() ${\mathcal{D}}_{1}^{N}$
associated with the family
${\mathcal{D}}_{1}^{N}$
associated with the family
![]() $\unicode[STIX]{x1D703}_{1}$
. It is the preimage in
$\unicode[STIX]{x1D703}_{1}$
. It is the preimage in
![]() ${\mathcal{W}}_{1}^{\circ }$
of the disc
${\mathcal{W}}_{1}^{\circ }$
of the disc
![]() $B_{2,h}$
via the immersion
$B_{2,h}$
via the immersion
![]() $\unicode[STIX]{x1D704}:{\mathcal{W}}_{1}^{\circ }\rightarrow {\mathcal{W}}_{2}^{\circ }$
defined in §9.2.
$\unicode[STIX]{x1D704}:{\mathcal{W}}_{1}^{\circ }\rightarrow {\mathcal{W}}_{2}^{\circ }$
defined in §9.2.
Proof. As all the coefficient rings are local and all the residual representations are absolutely irreducible, we can apply the results of §10 by replacing pseudocharacters everywhere with the associated representations, that exist by [Reference RouquierRou96, Corollary 5.2] and are defined over the ring of coefficients of the pseudocharacter by Carayol’s theorem [Reference CarayolCar94, Théorème 1].
Now the equivalence (i)
![]() $\;\Longleftrightarrow \;$
(ii) follows from Proposition 10.4(iv) applied to the rigid analytic variety
$\;\Longleftrightarrow \;$
(ii) follows from Proposition 10.4(iv) applied to the rigid analytic variety
![]() ${\mathcal{V}}_{2}=I$
. The equivalence (ii)
${\mathcal{V}}_{2}=I$
. The equivalence (ii)
![]() $\;\Longleftrightarrow \;$
(iii) follows from Proposition 10.4(iii) by checking that the slopes satisfy the required inequality: this is a consequence of Corollary 9.8 and Remark 9.10.
$\;\Longleftrightarrow \;$
(iii) follows from Proposition 10.4(iii) by checking that the slopes satisfy the required inequality: this is a consequence of Corollary 9.8 and Remark 9.10.
If condition (iii) is satisfied by some
![]() $\unicode[STIX]{x1D70C}_{P_{0},1}$
, then
$\unicode[STIX]{x1D70C}_{P_{0},1}$
, then
![]() $\unicode[STIX]{x1D70C}_{P_{0},1}=\unicode[STIX]{x1D70C}_{P,1}|_{H_{0}}$
satisfies condition (iv). If condition (iv) holds, then the image of
$\unicode[STIX]{x1D70C}_{P_{0},1}=\unicode[STIX]{x1D70C}_{P,1}|_{H_{0}}$
satisfies condition (iv). If condition (iv) holds, then the image of
![]() $\unicode[STIX]{x1D70C}_{P_{0}}$
is contained in
$\unicode[STIX]{x1D70C}_{P_{0}}$
is contained in
![]() $\operatorname{Sym}^{3}\operatorname{GL}_{2}(\mathbb{I}_{0}^{\circ }/\mathfrak{I})$
. As
$\operatorname{Sym}^{3}\operatorname{GL}_{2}(\mathbb{I}_{0}^{\circ }/\mathfrak{I})$
. As
![]() $\unicode[STIX]{x1D70C}_{P_{0}}=\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }}|_{H_{0}}$
Lemma 3.14 implies that, after extending the coefficients to a finite extension
$\unicode[STIX]{x1D70C}_{P_{0}}=\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }}|_{H_{0}}$
Lemma 3.14 implies that, after extending the coefficients to a finite extension
![]() $\mathbb{I}_{0}^{\prime }$
of
$\mathbb{I}_{0}^{\prime }$
of
![]() $\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
the image of
$\mathbb{I}_{\operatorname{Tr}}^{\circ }/P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }$
the image of
![]() $\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }}$
is contained in
$\unicode[STIX]{x1D70C}_{P_{0}\mathbb{I}_{\operatorname{Tr}}^{\circ }}$
is contained in
![]() $\operatorname{Sym}^{3}\operatorname{GL}_{2}(\mathbb{I}_{0}^{\prime })$
. This gives condition (ii), completing the proof.◻
$\operatorname{Sym}^{3}\operatorname{GL}_{2}(\mathbb{I}_{0}^{\prime })$
. This gives condition (ii), completing the proof.◻
We gather some information on the congruence ideal.
Lemma 11.3.
(i) The ideal
 $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
is of height one. In particular, it is non-zero.
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
is of height one. In particular, it is non-zero.(ii) If there is no representation
 $\overline{\unicode[STIX]{x1D70C}}_{1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{F}}_{p})$
satisfying
$\overline{\unicode[STIX]{x1D70C}}_{1}:G_{\mathbb{Q}}\rightarrow \operatorname{GL}_{2}(\overline{\mathbb{F}}_{p})$
satisfying
 $\overline{\unicode[STIX]{x1D70C}}\cong \operatorname{Sym}^{3}\overline{\unicode[STIX]{x1D70C}}_{1}$
, then
$\overline{\unicode[STIX]{x1D70C}}\cong \operatorname{Sym}^{3}\overline{\unicode[STIX]{x1D70C}}_{1}$
, then
 $\mathfrak{c}_{\unicode[STIX]{x1D703}}=\mathbb{I}_{0}^{\circ }$
.
$\mathfrak{c}_{\unicode[STIX]{x1D703}}=\mathbb{I}_{0}^{\circ }$
.(iii) Suppose that there exists a non-CM classical point
 $x\in {\mathcal{D}}_{1}^{N}$
of weight
$x\in {\mathcal{D}}_{1}^{N}$
of weight
 $k$
such that
$k$
such that
 $\operatorname{sl}(x)\leqslant h/7$
and
$\operatorname{sl}(x)\leqslant h/7$
and
 $\unicode[STIX]{x1D704}(k)\in B_{2,h}$
and
$\unicode[STIX]{x1D704}(k)\in B_{2,h}$
and
 $k>h-4$
. Then there exists a family
$k>h-4$
. Then there exists a family
 $\unicode[STIX]{x1D703}$
of
$\unicode[STIX]{x1D703}$
of
 $\operatorname{GSp}_{4}$
-eigenforms of slope bounded by
$\operatorname{GSp}_{4}$
-eigenforms of slope bounded by
 $h$
such that
$h$
such that
 $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
has a prime divisor of height
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
has a prime divisor of height
 $1$
.
$1$
.
Proof. Part (i) is an immediate consequence of Corollary 10.6. Part (ii) follows trivially from the definition of
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
. We prove part (iii). Let
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
. We prove part (iii). Let
![]() $x$
be a point satisfying the assumptions of part (iii) and let
$x$
be a point satisfying the assumptions of part (iii) and let
![]() $f$
be the corresponding classical
$f$
be the corresponding classical
![]() $\operatorname{GL}_{2}$
-eigenform. Let
$\operatorname{GL}_{2}$
-eigenform. Let
![]() $\operatorname{Sym}^{3}x$
be the point of
$\operatorname{Sym}^{3}x$
be the point of
![]() ${\mathcal{D}}_{2}^{M}$
that corresponds to the form
${\mathcal{D}}_{2}^{M}$
that corresponds to the form
![]() $(\operatorname{Sym}^{3}f)_{1}^{\operatorname{st}}$
defined in Proposition 9.7. Let
$(\operatorname{Sym}^{3}f)_{1}^{\operatorname{st}}$
defined in Proposition 9.7. Let
![]() $\unicode[STIX]{x1D709}:{\mathcal{D}}_{1}^{N,{\mathcal{G}}}\rightarrow {\mathcal{D}}_{2}^{M}$
be the map of rigid analytic spaces given by Proposition 9.11. The image of an irreducible component
$\unicode[STIX]{x1D709}:{\mathcal{D}}_{1}^{N,{\mathcal{G}}}\rightarrow {\mathcal{D}}_{2}^{M}$
be the map of rigid analytic spaces given by Proposition 9.11. The image of an irreducible component
![]() $J$
of
$J$
of
![]() ${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
containing
${\mathcal{D}}_{1}^{N,{\mathcal{G}}}$
containing
![]() $x$
is an irreducible component of
$x$
is an irreducible component of
![]() ${\mathcal{D}}_{2}^{M}$
that contains
${\mathcal{D}}_{2}^{M}$
that contains
![]() $\unicode[STIX]{x1D709}(J)$
. By Corollary 9.8, we have
$\unicode[STIX]{x1D709}(J)$
. By Corollary 9.8, we have
![]() $\operatorname{sl}(\operatorname{Sym}^{3}x)\leqslant h$
. As
$\operatorname{sl}(\operatorname{Sym}^{3}x)\leqslant h$
. As
![]() $k+1>h-3$
, the weight map is étale at the point
$k+1>h-3$
, the weight map is étale at the point
![]() $\operatorname{Sym}^{3}x$
, so there exists only one irreducible component of
$\operatorname{Sym}^{3}x$
, so there exists only one irreducible component of
![]() ${\mathcal{D}}_{2}^{M}$
containing
${\mathcal{D}}_{2}^{M}$
containing
![]() $\operatorname{Sym}^{3}x$
. We denote by
$\operatorname{Sym}^{3}x$
. We denote by
![]() $\unicode[STIX]{x1D703}$
the finite slope family supported in such a component and containing
$\unicode[STIX]{x1D703}$
the finite slope family supported in such a component and containing
![]() $\operatorname{Sym}^{3}x$
, and by
$\operatorname{Sym}^{3}x$
, and by
![]() $I$
the support of
$I$
the support of
![]() $\unicode[STIX]{x1D703}$
. By our last remark, the space
$\unicode[STIX]{x1D703}$
. By our last remark, the space
![]() $\unicode[STIX]{x1D709}(J)$
intersects the admissible domain
$\unicode[STIX]{x1D709}(J)$
intersects the admissible domain
![]() $I$
in a one-dimensional subspace. The ideal of
$I$
in a one-dimensional subspace. The ideal of
![]() $\mathbb{I}^{\circ }={\mathcal{O}}(I)^{\circ }$
consisting of elements that vanish on
$\mathbb{I}^{\circ }={\mathcal{O}}(I)^{\circ }$
consisting of elements that vanish on
![]() $\unicode[STIX]{x1D709}(J)$
is a height-one ideal of
$\unicode[STIX]{x1D709}(J)$
is a height-one ideal of
![]() $I$
that divides the congruence ideal
$I$
that divides the congruence ideal
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
. In particular,
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
. In particular,
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
admits a height-one prime divisor.◻
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
admits a height-one prime divisor.◻
The fortuitous
![]() $\operatorname{Sym}^{3}$
-congruence ideal is an analogue of the congruence ideal of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Definition 3.10]. There is an important difference between the situation studied here and in [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] and those treated in [Reference HidaHid15, Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15]. In [Reference HidaHid15, Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15], the congruence ideal describes the locus of intersection between a fixed ‘general’ family (i.e. such that its specializations are not lifts of forms from a smaller group) and the ‘non-general’ families. Such non-general families are obtained as the
$\operatorname{Sym}^{3}$
-congruence ideal is an analogue of the congruence ideal of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Definition 3.10]. There is an important difference between the situation studied here and in [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16] and those treated in [Reference HidaHid15, Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15]. In [Reference HidaHid15, Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15], the congruence ideal describes the locus of intersection between a fixed ‘general’ family (i.e. such that its specializations are not lifts of forms from a smaller group) and the ‘non-general’ families. Such non-general families are obtained as the
![]() $p$
-adic lift of families of overconvergent eigenforms for smaller groups (e.g.
$p$
-adic lift of families of overconvergent eigenforms for smaller groups (e.g.
![]() $\operatorname{GL}_{1/K}$
for an imaginary quadratic field
$\operatorname{GL}_{1/K}$
for an imaginary quadratic field
![]() $K$
in the case of CM families of
$K$
in the case of CM families of
![]() $\operatorname{GL}_{2}$
-eigenforms, as in [Reference HidaHid15], and
$\operatorname{GL}_{2}$
-eigenforms, as in [Reference HidaHid15], and
![]() $\operatorname{GL}_{2/F}$
for a real quadratic field
$\operatorname{GL}_{2/F}$
for a real quadratic field
![]() $F$
in the case of ‘twisted Yoshida type’ families of
$F$
in the case of ‘twisted Yoshida type’ families of
![]() $\operatorname{GSp}_{4}$
-eigenforms, as in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15]). In our setting, there are no non-general families: the overconvergent
$\operatorname{GSp}_{4}$
-eigenforms, as in [Reference Hida, Tilouine, Dieulefait, Faltings, Heath-Brown, Manin, Moroz and WintenbergerHT15]). In our setting, there are no non-general families: the overconvergent
![]() $\operatorname{GSp}_{4}$
-eigenforms that are lifts of overconvergent eigenforms for smaller groups must be of
$\operatorname{GSp}_{4}$
-eigenforms that are lifts of overconvergent eigenforms for smaller groups must be of
![]() $\operatorname{Sym}^{3}$
type by Lemma 3.15 and Theorem 3.8, and we know that the
$\operatorname{Sym}^{3}$
type by Lemma 3.15 and Theorem 3.8, and we know that the
![]() $\operatorname{Sym}^{3}$
-locus on the
$\operatorname{Sym}^{3}$
-locus on the
![]() $\operatorname{GSp}_{4}$
-eigenvariety does not contain any two-dimensional irreducible component by Lemma 11.3(i). Hence, the ideal
$\operatorname{GSp}_{4}$
-eigenvariety does not contain any two-dimensional irreducible component by Lemma 11.3(i). Hence, the ideal
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
measures the locus of points that are of
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
measures the locus of points that are of
![]() $\operatorname{Sym}^{3}$
type, without belonging to a two-dimensional family of
$\operatorname{Sym}^{3}$
type, without belonging to a two-dimensional family of
![]() $\operatorname{Sym}^{3}$
type. For this reason, we call it the ‘fortuitous’
$\operatorname{Sym}^{3}$
type. For this reason, we call it the ‘fortuitous’
![]() $\operatorname{Sym}^{3}$
-congruence ideal. This is a higher-dimensional analogue of the situation of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16], where it is shown that the positive slope CM points do not form one-dimensional families, but appear as isolated points on the irreducible components of the eigencurve (see [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Corollary 3.6]).
$\operatorname{Sym}^{3}$
-congruence ideal. This is a higher-dimensional analogue of the situation of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16], where it is shown that the positive slope CM points do not form one-dimensional families, but appear as isolated points on the irreducible components of the eigencurve (see [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Corollary 3.6]).
11.2 Comparison of the Galois level with the congruence ideal
In §8, we attached a Galois level to a family of finite slope
![]() $\operatorname{GSp}_{4}$
-eigenforms. The goal of this section is to compare this Galois theoretic objects with the congruence ideal introduced in §11.1, that is an object defined in terms of congruences of overconvergent automorphic forms.
$\operatorname{GSp}_{4}$
-eigenforms. The goal of this section is to compare this Galois theoretic objects with the congruence ideal introduced in §11.1, that is an object defined in terms of congruences of overconvergent automorphic forms.
We work in the setting of Theorem 8.1. In particular,
![]() $h$
is a positive rational number,
$h$
is a positive rational number,
![]() $\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
is a family of
$\unicode[STIX]{x1D703}:\mathbb{T}_{h}\rightarrow \mathbb{I}^{\circ }$
is a family of
![]() $\operatorname{GSp}_{4}$
-eigenforms of slope bounded by
$\operatorname{GSp}_{4}$
-eigenforms of slope bounded by
![]() $h$
and
$h$
and
![]() $\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
is the Galois representation associated with
$\unicode[STIX]{x1D70C}:G_{\mathbb{Q}}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{\operatorname{Tr}}^{\circ })$
is the Galois representation associated with
![]() $\unicode[STIX]{x1D703}$
. We make the same assumptions on
$\unicode[STIX]{x1D703}$
. We make the same assumptions on
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D70C}$
as in Theorem 8.1; in particular,
$\unicode[STIX]{x1D70C}$
as in Theorem 8.1; in particular,
![]() $\unicode[STIX]{x1D70C}$
is
$\unicode[STIX]{x1D70C}$
is
![]() $\mathbb{Z}_{p}$
-regular and the residual representation
$\mathbb{Z}_{p}$
-regular and the residual representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
is either full or of symmetric cube type. With the family
$\overline{\unicode[STIX]{x1D70C}}$
is either full or of symmetric cube type. With the family
![]() $\unicode[STIX]{x1D703}$
we associate two ideals of
$\unicode[STIX]{x1D703}$
we associate two ideals of
![]() $\mathbb{I}_{0}$
:
$\mathbb{I}_{0}$
:
– the ideal
 $\mathfrak{c}_{\unicode[STIX]{x1D703}}\cdot \mathbb{I}_{0}$
, where
$\mathfrak{c}_{\unicode[STIX]{x1D703}}\cdot \mathbb{I}_{0}$
, where
 $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
is the fortuitous
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
is the fortuitous
 $(\operatorname{Sym}^{3},\mathbb{I}_{0}^{\circ })$
-congruence ideal (see Definition 11.1);
$(\operatorname{Sym}^{3},\mathbb{I}_{0}^{\circ })$
-congruence ideal (see Definition 11.1);– the Galois level
 $\mathfrak{l}_{\unicode[STIX]{x1D703}}$
(see Definition 8.4).
$\mathfrak{l}_{\unicode[STIX]{x1D703}}$
(see Definition 8.4).
To simplify notation, we write
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
for
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
for
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}\cdot \mathbb{I}_{0}$
. For every ring
$\mathfrak{c}_{\unicode[STIX]{x1D703}}\cdot \mathbb{I}_{0}$
. For every ring
![]() $R$
and every ideal
$R$
and every ideal
![]() $\mathfrak{I}$
of
$\mathfrak{I}$
of
![]() $R$
, we denote by
$R$
, we denote by
![]() $V_{R}(\mathfrak{I})$
the set of primes of
$V_{R}(\mathfrak{I})$
the set of primes of
![]() $R$
containing
$R$
containing
![]() $\mathfrak{I}$
. The theorem below is an analogue of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Theorem 6.2]. The set
$\mathfrak{I}$
. The theorem below is an analogue of [Reference Conti, Iovita, Tilouine, Loeffler and ZerbesCIT16, Theorem 6.2]. The set
![]() $S^{\operatorname{bad}}$
of ‘bad’ primes of
$S^{\operatorname{bad}}$
of ‘bad’ primes of
![]() $\mathbb{I}_{0}^{\circ }$
was defined in §7.1. Note that
$\mathbb{I}_{0}^{\circ }$
was defined in §7.1. Note that
![]() $V_{\mathbb{I}_{0}}(\mathfrak{l}_{\unicode[STIX]{x1D703}})\cap S^{\operatorname{bad}}$
is empty because the property defining the Galois level only involves
$V_{\mathbb{I}_{0}}(\mathfrak{l}_{\unicode[STIX]{x1D703}})\cap S^{\operatorname{bad}}$
is empty because the property defining the Galois level only involves
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}\cdot \mathbb{B}_{r}$
, and the primes in
$\mathfrak{l}_{\unicode[STIX]{x1D703}}\cdot \mathbb{B}_{r}$
, and the primes in
![]() $S^{\operatorname{bad}}$
are invertible in
$S^{\operatorname{bad}}$
are invertible in
![]() $\mathbb{B}_{r}$
.
$\mathbb{B}_{r}$
.
Theorem 11.4. There is an equality of sets
![]() $V_{\mathbb{I}_{0}}(\mathfrak{c}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}=V_{\mathbb{I}_{0}}(\mathfrak{l}_{\unicode[STIX]{x1D703}})$
.
$V_{\mathbb{I}_{0}}(\mathfrak{c}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}=V_{\mathbb{I}_{0}}(\mathfrak{l}_{\unicode[STIX]{x1D703}})$
.
Recall that there is a natural inclusion
![]() $\unicode[STIX]{x1D704}_{r}:\mathbb{I}_{0}{\hookrightarrow}\mathbb{I}_{r,0}$
.
$\unicode[STIX]{x1D704}_{r}:\mathbb{I}_{0}{\hookrightarrow}\mathbb{I}_{r,0}$
.
Proof. First we prove that
![]() $V_{\mathbb{I}_{0}}(\mathfrak{c}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}\subset V_{\mathbb{I}_{0}}(\mathfrak{l}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}$
. Choose a radius
$V_{\mathbb{I}_{0}}(\mathfrak{c}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}\subset V_{\mathbb{I}_{0}}(\mathfrak{l}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}$
. Choose a radius
![]() $r$
in the set
$r$
in the set
![]() $\{r_{i}\}\text{}_{i\in \mathbb{N}^{{>}0}}$
defined in §4. Let
$\{r_{i}\}\text{}_{i\in \mathbb{N}^{{>}0}}$
defined in §4. Let
![]() $P\in V_{\mathbb{I}_{0}}(\mathfrak{c}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}$
and let
$P\in V_{\mathbb{I}_{0}}(\mathfrak{c}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}$
and let
![]() $\unicode[STIX]{x1D70C}_{P}$
be the reduction of
$\unicode[STIX]{x1D70C}_{P}$
be the reduction of
![]() $\unicode[STIX]{x1D70C}|_{H_{0}}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0})$
modulo
$\unicode[STIX]{x1D70C}|_{H_{0}}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{0})$
modulo
![]() $P$
. By Proposition 11.2 there exists a representation
$P$
. By Proposition 11.2 there exists a representation
![]() $\unicode[STIX]{x1D70C}_{P,1}:H_{0}\rightarrow \operatorname{GL}_{2}(\mathbb{I}_{0}/P)$
such that
$\unicode[STIX]{x1D70C}_{P,1}:H_{0}\rightarrow \operatorname{GL}_{2}(\mathbb{I}_{0}/P)$
such that
![]() $\unicode[STIX]{x1D70C}_{P}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{P,1}$
. Let
$\unicode[STIX]{x1D70C}_{P}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{P,1}$
. Let
![]() $\unicode[STIX]{x1D70C}_{r,P}=\unicode[STIX]{x1D704}_{r}\circ \,\unicode[STIX]{x1D70C}_{P}$
and
$\unicode[STIX]{x1D70C}_{r,P}=\unicode[STIX]{x1D704}_{r}\circ \,\unicode[STIX]{x1D70C}_{P}$
and
![]() $\unicode[STIX]{x1D70C}_{r,P,1}=\unicode[STIX]{x1D704}_{r}\circ \,\unicode[STIX]{x1D70C}_{P,1}$
. The isomorphism above gives
$\unicode[STIX]{x1D70C}_{r,P,1}=\unicode[STIX]{x1D704}_{r}\circ \,\unicode[STIX]{x1D70C}_{P,1}$
. The isomorphism above gives
![]() $\unicode[STIX]{x1D70C}_{r,P}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{r,P,1}$
.
$\unicode[STIX]{x1D70C}_{r,P}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{r,P,1}$
.
Suppose by contradiction that
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}\not \subset P$
. By the definition of
$\mathfrak{l}_{\unicode[STIX]{x1D703}}\not \subset P$
. By the definition of
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}$
, we have
$\mathfrak{l}_{\unicode[STIX]{x1D703}}$
, we have
![]() $\mathfrak{G}_{r}\supset \mathfrak{l}_{\unicode[STIX]{x1D703}}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})$
. Recall that
$\mathfrak{G}_{r}\supset \mathfrak{l}_{\unicode[STIX]{x1D703}}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})$
. Recall that
![]() $\mathbb{B}_{r}/P=\mathbb{I}_{r,0}/P$
by the construction of
$\mathbb{B}_{r}/P=\mathbb{I}_{r,0}/P$
by the construction of
![]() $\mathbb{B}_{r}$
. By looking at the previous inclusion modulo
$\mathbb{B}_{r}$
. By looking at the previous inclusion modulo
![]() $P$
, we obtain
$P$
, we obtain
As
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}\not \subset P$
, we have
$\mathfrak{l}_{\unicode[STIX]{x1D703}}\not \subset P$
, we have
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}/(P\cap \mathfrak{l}_{\unicode[STIX]{x1D703}})\neq 0$
. By definition,
$\mathfrak{l}_{\unicode[STIX]{x1D703}}/(P\cap \mathfrak{l}_{\unicode[STIX]{x1D703}})\neq 0$
. By definition,
![]() $\mathfrak{G}_{r,P}=\mathbb{Q}_{p}\cdot \log \operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}$
. By our previous argument
$\mathfrak{G}_{r,P}=\mathbb{Q}_{p}\cdot \log \operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}$
. By our previous argument
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}\subset \operatorname{Sym}^{3}\operatorname{GL}_{2}(\mathbb{I}_{r,0}/P\mathbb{I}_{r,0})$
, so
$\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}\subset \operatorname{Sym}^{3}\operatorname{GL}_{2}(\mathbb{I}_{r,0}/P\mathbb{I}_{r,0})$
, so
![]() $\log \operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}$
cannot contain a subalgebra of the form
$\log \operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}$
cannot contain a subalgebra of the form
![]() $\mathfrak{I}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0}/P\mathbb{I}_{r,0})$
for a non-zero ideal
$\mathfrak{I}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{I}_{r,0}/P\mathbb{I}_{r,0})$
for a non-zero ideal
![]() $\mathfrak{I}$
of
$\mathfrak{I}$
of
![]() $\mathbb{I}_{r,0}/P\mathbb{I}_{r,0}$
. This contradicts (39).
$\mathbb{I}_{r,0}/P\mathbb{I}_{r,0}$
. This contradicts (39).
We prove the inclusion
![]() $V_{\mathbb{I}_{0}}(\mathfrak{l}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}\subset V_{\mathbb{I}_{0}}(\mathfrak{c}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}$
. Let
$V_{\mathbb{I}_{0}}(\mathfrak{l}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}\subset V_{\mathbb{I}_{0}}(\mathfrak{c}_{\unicode[STIX]{x1D703}})-S^{\operatorname{bad}}$
. Let
![]() $P$
be a prime of
$P$
be a prime of
![]() $\mathbb{I}_{0}$
. We have to show that if
$\mathbb{I}_{0}$
. We have to show that if
![]() $P\notin S^{\operatorname{bad}}$
and
$P\notin S^{\operatorname{bad}}$
and
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}\subset P$
, then
$\mathfrak{l}_{\unicode[STIX]{x1D703}}\subset P$
, then
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}\subset P$
. Every prime of
$\mathfrak{c}_{\unicode[STIX]{x1D703}}\subset P$
. Every prime of
![]() $\mathbb{I}_{0}$
is the intersection of the maximal ideals that contain it, so it is sufficient to show the previous implication when
$\mathbb{I}_{0}$
is the intersection of the maximal ideals that contain it, so it is sufficient to show the previous implication when
![]() $P$
is a maximal ideal.
$P$
is a maximal ideal.
Let
![]() $P$
be a maximal ideal of
$P$
be a maximal ideal of
![]() $\mathbb{I}_{0}$
such that
$\mathbb{I}_{0}$
such that
![]() $P\notin S^{\operatorname{bad}}$
and
$P\notin S^{\operatorname{bad}}$
and
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}\subset P$
. Let
$\mathfrak{l}_{\unicode[STIX]{x1D703}}\subset P$
. Let
![]() $\unicode[STIX]{x1D705}_{P}$
be the residue field
$\unicode[STIX]{x1D705}_{P}$
be the residue field
![]() $\mathbb{I}_{0}/P$
. We define two ideals of
$\mathbb{I}_{0}/P$
. We define two ideals of
![]() $\mathbb{I}_{r,0}$
by
$\mathbb{I}_{r,0}$
by
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703},r}=\unicode[STIX]{x1D704}_{r}(\mathfrak{l}_{\unicode[STIX]{x1D703}})\mathbb{I}_{r,0}$
and
$\mathfrak{l}_{\unicode[STIX]{x1D703},r}=\unicode[STIX]{x1D704}_{r}(\mathfrak{l}_{\unicode[STIX]{x1D703}})\mathbb{I}_{r,0}$
and
![]() $P_{r}=\unicode[STIX]{x1D704}_{r}(P)\mathbb{I}_{r,0}$
. Note that
$P_{r}=\unicode[STIX]{x1D704}_{r}(P)\mathbb{I}_{r,0}$
. Note that
![]() $\unicode[STIX]{x1D704}_{r}$
induces an isomorphism
$\unicode[STIX]{x1D704}_{r}$
induces an isomorphism
![]() $\mathbb{I}_{0}/P\cong \mathbb{I}_{r,0}/P_{r}$
. In particular,
$\mathbb{I}_{0}/P\cong \mathbb{I}_{r,0}/P_{r}$
. In particular,
![]() $P_{r}$
is maximal in
$P_{r}$
is maximal in
![]() $\mathbb{I}_{r,0}$
and
$\mathbb{I}_{r,0}$
and
![]() $\mathbb{I}_{r,0}/P_{r}\cong \unicode[STIX]{x1D705}_{P}$
, which is a local field.
$\mathbb{I}_{r,0}/P_{r}\cong \unicode[STIX]{x1D705}_{P}$
, which is a local field.
As before, let
![]() $\unicode[STIX]{x1D70C}_{r,P}=\unicode[STIX]{x1D704}_{r}\circ \,\unicode[STIX]{x1D70C}_{P}$
. The residual representation
$\unicode[STIX]{x1D70C}_{r,P}=\unicode[STIX]{x1D704}_{r}\circ \,\unicode[STIX]{x1D70C}_{P}$
. The residual representation
![]() $\overline{\unicode[STIX]{x1D70C}}_{r,P}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r,0}^{\circ }/\mathfrak{m}_{\mathbb{I}_{r,0}^{\circ }})$
associated with
$\overline{\unicode[STIX]{x1D70C}}_{r,P}:H_{0}\rightarrow \operatorname{GSp}_{4}(\mathbb{I}_{r,0}^{\circ }/\mathfrak{m}_{\mathbb{I}_{r,0}^{\circ }})$
associated with
![]() $\unicode[STIX]{x1D70C}_{r,P}$
coincides with
$\unicode[STIX]{x1D70C}_{r,P}$
coincides with
![]() $\overline{\unicode[STIX]{x1D70C}}|_{H_{0}}$
. In particular,
$\overline{\unicode[STIX]{x1D70C}}|_{H_{0}}$
. In particular,
![]() $\unicode[STIX]{x1D70C}_{r,P}$
is of residual
$\unicode[STIX]{x1D70C}_{r,P}$
is of residual
![]() $\operatorname{Sym}^{3}$
type in the sense of Definition 3.11. Let
$\operatorname{Sym}^{3}$
type in the sense of Definition 3.11. Let
![]() $G_{r,P}=\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}$
and
$G_{r,P}=\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}$
and
![]() $G_{r,P}^{\circ }$
be the connected component of the identity in
$G_{r,P}^{\circ }$
be the connected component of the identity in
![]() $G_{r,P}$
. Let
$G_{r,P}$
. Let
![]() $\overline{G_{r,P}^{\circ }}^{\operatorname{Zar}}$
be the Zariski-closure of
$\overline{G_{r,P}^{\circ }}^{\operatorname{Zar}}$
be the Zariski-closure of
![]() $G_{r,P}^{\circ }$
in
$G_{r,P}^{\circ }$
in
![]() $\operatorname{GSp}_{4}(\mathbb{I}_{r,0}/P_{r})$
. As
$\operatorname{GSp}_{4}(\mathbb{I}_{r,0}/P_{r})$
. As
![]() $\unicode[STIX]{x1D70C}_{r,P}$
is residually either full or of symmetric cube type, by the classification preceding Lemma 3.15 one of the following must hold:
$\unicode[STIX]{x1D70C}_{r,P}$
is residually either full or of symmetric cube type, by the classification preceding Lemma 3.15 one of the following must hold:
(i) the algebraic group
 $\overline{G_{r,P}^{\circ }}^{\operatorname{Zar}}$
is isomorphic to
$\overline{G_{r,P}^{\circ }}^{\operatorname{Zar}}$
is isomorphic to
 $\operatorname{Sym}^{3}\operatorname{SL}_{2}$
over
$\operatorname{Sym}^{3}\operatorname{SL}_{2}$
over
 $\mathbb{I}_{r,0}/P_{r}$
;
$\mathbb{I}_{r,0}/P_{r}$
;(ii) the algebraic group
 $\overline{G_{r,P}^{\circ }}^{\operatorname{Zar}}$
is isomorphic to
$\overline{G_{r,P}^{\circ }}^{\operatorname{Zar}}$
is isomorphic to
 $\operatorname{Sp}_{4}$
over
$\operatorname{Sp}_{4}$
over
 $\mathbb{I}_{r,0}/P_{r}$
.
$\mathbb{I}_{r,0}/P_{r}$
.
In both cases, let
![]() $H^{0}$
denote the normal open subgroup of
$H^{0}$
denote the normal open subgroup of
![]() $H_{0}$
satisfying
$H_{0}$
satisfying
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}|_{H^{0}}=G_{r,P}^{\circ }$
. As
$\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}|_{H^{0}}=G_{r,P}^{\circ }$
. As
![]() $H_{0}$
is open and normal in
$H_{0}$
is open and normal in
![]() $G_{\mathbb{Q}}$
,
$G_{\mathbb{Q}}$
,
![]() $H^{0}$
is also open and normal in
$H^{0}$
is also open and normal in
![]() $G_{\mathbb{Q}}$
. In case (i), there exists a representation
$G_{\mathbb{Q}}$
. In case (i), there exists a representation
![]() $\unicode[STIX]{x1D70C}_{r,P}^{0}:H^{0}\rightarrow \operatorname{GL}_{2}(\mathbb{I}_{r,0}/P_{r})$
such that
$\unicode[STIX]{x1D70C}_{r,P}^{0}:H^{0}\rightarrow \operatorname{GL}_{2}(\mathbb{I}_{r,0}/P_{r})$
such that
![]() $\unicode[STIX]{x1D70C}_{r,P}|_{H^{0}}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{r,P}^{0}$
. As the image of
$\unicode[STIX]{x1D70C}_{r,P}|_{H^{0}}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{r,P}^{0}$
. As the image of
![]() $\unicode[STIX]{x1D70C}_{r,P}|_{H^{0}}$
is Zariski-dense in the copy of
$\unicode[STIX]{x1D70C}_{r,P}|_{H^{0}}$
is Zariski-dense in the copy of
![]() $\operatorname{SL}_{2}(\mathbb{I}_{r,0}/P_{r})$
embedded via the symmetric cube map, the image of
$\operatorname{SL}_{2}(\mathbb{I}_{r,0}/P_{r})$
embedded via the symmetric cube map, the image of
![]() $\unicode[STIX]{x1D70C}_{r,P}^{0}$
is Zariski-dense in
$\unicode[STIX]{x1D70C}_{r,P}^{0}$
is Zariski-dense in
![]() $\operatorname{SL}_{2}(\mathbb{I}_{r,0}/P_{r})$
. From Lemma 3.14, we deduce that
$\operatorname{SL}_{2}(\mathbb{I}_{r,0}/P_{r})$
. From Lemma 3.14, we deduce that
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}^{0}$
contains a congruence subgroup of
$\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}^{0}$
contains a congruence subgroup of
![]() $\operatorname{SL}_{2}(\mathbb{I}_{r,0}/P_{r})$
. Now the hypotheses of Lemma 3.14 are satisfied by the representation
$\operatorname{SL}_{2}(\mathbb{I}_{r,0}/P_{r})$
. Now the hypotheses of Lemma 3.14 are satisfied by the representation
![]() $\unicode[STIX]{x1D70C}_{r,P}^{0}$
and the group
$\unicode[STIX]{x1D70C}_{r,P}^{0}$
and the group
![]() $H^{0}$
, so we conclude that there exists a representation
$H^{0}$
, so we conclude that there exists a representation
![]() $\unicode[STIX]{x1D70C}_{H_{0},r,P}^{\prime }:H_{0}\rightarrow \operatorname{GL}_{2}(\mathbb{I}_{r,0}/P_{r})$
such that
$\unicode[STIX]{x1D70C}_{H_{0},r,P}^{\prime }:H_{0}\rightarrow \operatorname{GL}_{2}(\mathbb{I}_{r,0}/P_{r})$
such that
![]() $\unicode[STIX]{x1D70C}_{H_{0},r,P}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{H_{0},r,P}^{\prime }$
. By Lemma 11.2, the prime
$\unicode[STIX]{x1D70C}_{H_{0},r,P}\cong \operatorname{Sym}^{3}\unicode[STIX]{x1D70C}_{H_{0},r,P}^{\prime }$
. By Lemma 11.2, the prime
![]() $P$
must contain
$P$
must contain
![]() $\mathfrak{c}_{\unicode[STIX]{x1D703}}$
, as desired.
$\mathfrak{c}_{\unicode[STIX]{x1D703}}$
, as desired.
We show that case (ii) never occurs. Suppose by contradiction that
![]() $\overline{G_{H_{0},r,P}^{\circ }}^{\operatorname{Zar}}\cong \operatorname{Sp}_{4}$
over
$\overline{G_{H_{0},r,P}^{\circ }}^{\operatorname{Zar}}\cong \operatorname{Sp}_{4}$
over
![]() $\mathbb{I}_{r,0}/P_{r}$
. By Propositions 5.11 and 5.14, we know that the field
$\mathbb{I}_{r,0}/P_{r}$
. By Propositions 5.11 and 5.14, we know that the field
![]() $\mathbb{I}_{0}/P$
is generated over
$\mathbb{I}_{0}/P$
is generated over
![]() $\mathbb{Q}_{p}$
by the traces of
$\mathbb{Q}_{p}$
by the traces of
![]() $\operatorname{Ad}(\unicode[STIX]{x1D70C}_{P}|_{H_{0}})$
. Hence, the field
$\operatorname{Ad}(\unicode[STIX]{x1D70C}_{P}|_{H_{0}})$
. Hence, the field
![]() $\mathbb{I}_{r,0}/P_{r}$
is generated over
$\mathbb{I}_{r,0}/P_{r}$
is generated over
![]() $\mathbb{Q}_{p}$
by the traces of
$\mathbb{Q}_{p}$
by the traces of
![]() $\operatorname{Ad}\unicode[STIX]{x1D70C}_{r,P}$
. By Theorem 3.13 applied to
$\operatorname{Ad}\unicode[STIX]{x1D70C}_{r,P}$
. By Theorem 3.13 applied to
![]() $\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}$
, there exists a non-zero ideal
$\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}$
, there exists a non-zero ideal
![]() $\mathfrak{l}_{r,P}$
of
$\mathfrak{l}_{r,P}$
of
![]() $\mathbb{I}_{r,0}/P_{r}$
such that
$\mathbb{I}_{r,0}/P_{r}$
such that
![]() $G_{r,P}$
contains the principal congruence subgroup
$G_{r,P}$
contains the principal congruence subgroup
![]() $\unicode[STIX]{x1D6E4}_{\mathbb{I}_{r,0}/P_{r}}(\mathfrak{l}_{r,P})$
of
$\unicode[STIX]{x1D6E4}_{\mathbb{I}_{r,0}/P_{r}}(\mathfrak{l}_{r,P})$
of
![]() $\operatorname{Sp}_{4}(\mathbb{I}_{r,0}/P_{r})$
. By definition
$\operatorname{Sp}_{4}(\mathbb{I}_{r,0}/P_{r})$
. By definition
![]() $\mathfrak{G}_{r,P}=\mathbb{Q}_{p}\cdot \log (\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}|_{H_{r}})$
, where
$\mathfrak{G}_{r,P}=\mathbb{Q}_{p}\cdot \log (\operatorname{Im}\unicode[STIX]{x1D70C}_{r,P}|_{H_{r}})$
, where
![]() $H_{r}$
is open in
$H_{r}$
is open in
![]() $G_{\mathbb{Q}}$
, so up to replacing
$G_{\mathbb{Q}}$
, so up to replacing
![]() $\mathfrak{l}_{r,P}$
by a smaller non-zero ideal we have
$\mathfrak{l}_{r,P}$
by a smaller non-zero ideal we have
The algebras
![]() $\mathfrak{G}_{r,P}$
are independent of
$\mathfrak{G}_{r,P}$
are independent of
![]() $r$
in the sense of Remark 7.3, so there exists an ideal
$r$
in the sense of Remark 7.3, so there exists an ideal
![]() $\mathfrak{l}_{P}$
of
$\mathfrak{l}_{P}$
of
![]() $\mathbb{I}_{0}/P$
such that, for every
$\mathbb{I}_{0}/P$
such that, for every
![]() $r$
in the set
$r$
in the set
![]() $\{r_{i}\}\text{}_{i\geqslant 1}$
, the ideal
$\{r_{i}\}\text{}_{i\geqslant 1}$
, the ideal
![]() $\mathfrak{l}_{r,P}=\unicode[STIX]{x1D704}_{r}(\mathfrak{l}_{P})$
satisfies (40). We choose the ideals
$\mathfrak{l}_{r,P}=\unicode[STIX]{x1D704}_{r}(\mathfrak{l}_{P})$
satisfies (40). We choose the ideals
![]() $\mathfrak{l}_{r,P}$
of this form.
$\mathfrak{l}_{r,P}$
of this form.
As before,
![]() $\unicode[STIX]{x1D6E5}$
is the set of roots of
$\unicode[STIX]{x1D6E5}$
is the set of roots of
![]() $\operatorname{GSp}_{4}$
with respect to the chosen maximal torus. Let
$\operatorname{GSp}_{4}$
with respect to the chosen maximal torus. Let
![]() $\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Let
$\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}$
. Let
![]() $\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
and
$\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
and
![]() $\mathfrak{U}_{r,P_{r}}^{\unicode[STIX]{x1D6FC}}$
be the nilpotent Lie subalgebras of
$\mathfrak{U}_{r,P_{r}}^{\unicode[STIX]{x1D6FC}}$
be the nilpotent Lie subalgebras of
![]() $\mathfrak{G}_{r}$
and
$\mathfrak{G}_{r}$
and
![]() $\mathfrak{G}_{r,P_{r}}$
, respectively, corresponding to
$\mathfrak{G}_{r,P_{r}}$
, respectively, corresponding to
![]() $\unicode[STIX]{x1D6FC}$
. We denote by
$\unicode[STIX]{x1D6FC}$
. We denote by
![]() $\unicode[STIX]{x1D70B}_{P_{r}}$
the projection
$\unicode[STIX]{x1D70B}_{P_{r}}$
the projection
![]() $\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})\rightarrow \mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r}/P_{r}\mathbb{B}_{r})$
. Clearly
$\mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})\rightarrow \mathfrak{g}\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r}/P_{r}\mathbb{B}_{r})$
. Clearly
![]() $\mathfrak{G}_{r,P_{r}}=\unicode[STIX]{x1D70B}_{P_{r}}(\mathfrak{G}_{r})$
, so
$\mathfrak{G}_{r,P_{r}}=\unicode[STIX]{x1D70B}_{P_{r}}(\mathfrak{G}_{r})$
, so
![]() $\mathfrak{U}_{r,P_{r}}^{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D70B}_{P_{r}}(\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}})$
. Equation (40) gives
$\mathfrak{U}_{r,P_{r}}^{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D70B}_{P_{r}}(\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}})$
. Equation (40) gives
![]() $\mathfrak{l}_{r,P}\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{r,0}/P_{r})\subset \mathfrak{U}_{r,P_{r}}^{\unicode[STIX]{x1D6FC}}$
. Choose a subset
$\mathfrak{l}_{r,P}\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{r,0}/P_{r})\subset \mathfrak{U}_{r,P_{r}}^{\unicode[STIX]{x1D6FC}}$
. Choose a subset
![]() $A_{P}^{\unicode[STIX]{x1D6FC}}$
of
$A_{P}^{\unicode[STIX]{x1D6FC}}$
of
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0})$
such that, for every
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0})$
such that, for every
![]() $r$
,
$r$
,
![]() $\unicode[STIX]{x1D704}_{r}(A_{P}^{\unicode[STIX]{x1D6FC}})\subset \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
and
$\unicode[STIX]{x1D704}_{r}(A_{P}^{\unicode[STIX]{x1D6FC}})\subset \mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
and
![]() $\unicode[STIX]{x1D70B}_{P_{r}}(\unicode[STIX]{x1D704}_{r}(A_{P}^{\unicode[STIX]{x1D6FC}}))=\mathfrak{l}_{r,P}\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{r,0}/P_{r})$
. Such a set exists because the algebras
$\unicode[STIX]{x1D70B}_{P_{r}}(\unicode[STIX]{x1D704}_{r}(A_{P}^{\unicode[STIX]{x1D6FC}}))=\mathfrak{l}_{r,P}\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{r,0}/P_{r})$
. Such a set exists because the algebras
![]() $\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
are independent of
$\mathfrak{U}_{r}^{\unicode[STIX]{x1D6FC}}$
are independent of
![]() $r$
by Remark 7.3 and the ideals
$r$
by Remark 7.3 and the ideals
![]() $\mathfrak{l}_{r,P}$
have been chosen of the form
$\mathfrak{l}_{r,P}$
have been chosen of the form
![]() $\unicode[STIX]{x1D704}_{r}(\mathfrak{l}_{P})$
. Let
$\unicode[STIX]{x1D704}_{r}(\mathfrak{l}_{P})$
. Let
![]() $\mathfrak{A}_{P}$
be the ideal generated by
$\mathfrak{A}_{P}$
be the ideal generated by
![]() $A_{P}$
in
$A_{P}$
in
![]() $\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0})$
and set
$\mathfrak{u}^{\unicode[STIX]{x1D6FC}}(\mathbb{I}_{0})$
and set
![]() $\mathfrak{A}_{P}=\left(\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\mathfrak{A}_{P}^{\unicode[STIX]{x1D6FC}}\right)^{4}$
. By the same argument as in the proof of Theorem 8.1, the ideal
$\mathfrak{A}_{P}=\left(\prod _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}}\mathfrak{A}_{P}^{\unicode[STIX]{x1D6FC}}\right)^{4}$
. By the same argument as in the proof of Theorem 8.1, the ideal
![]() $\mathfrak{A}_{P}$
satisfies
$\mathfrak{A}_{P}$
satisfies
As
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})\subset \mathfrak{G}_{r}$
for every
$\mathfrak{l}_{\unicode[STIX]{x1D703}}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})\subset \mathfrak{G}_{r}$
for every
![]() $r$
, we also have
$r$
, we also have
![]() $(\mathfrak{l}_{\unicode[STIX]{x1D703}}+\mathfrak{A}_{P}^{\unicode[STIX]{x1D6FC}})\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})\subset \mathfrak{G}_{r}$
for every
$(\mathfrak{l}_{\unicode[STIX]{x1D703}}+\mathfrak{A}_{P}^{\unicode[STIX]{x1D6FC}})\mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})\subset \mathfrak{G}_{r}$
for every
![]() $r$
.
$r$
.
By assumption
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}\subset P$
, so
$\mathfrak{l}_{\unicode[STIX]{x1D703}}\subset P$
, so
![]() $\unicode[STIX]{x1D70B}_{P}(\mathfrak{l}_{\unicode[STIX]{x1D703}})=0$
. By the definition of
$\unicode[STIX]{x1D70B}_{P}(\mathfrak{l}_{\unicode[STIX]{x1D703}})=0$
. By the definition of
![]() $\mathfrak{A}_{P}$
, we have
$\mathfrak{A}_{P}$
, we have
![]() $\unicode[STIX]{x1D70B}_{P}(\mathfrak{A}_{P})\supset \unicode[STIX]{x1D70B}_{P}(A_{P})=\mathfrak{l}_{P}$
, so
$\unicode[STIX]{x1D70B}_{P}(\mathfrak{A}_{P})\supset \unicode[STIX]{x1D70B}_{P}(A_{P})=\mathfrak{l}_{P}$
, so
![]() $\unicode[STIX]{x1D70B}_{P}(\mathfrak{l}_{\unicode[STIX]{x1D703}}+\mathfrak{A}_{P})=\mathfrak{l}_{P}$
. We deduce that
$\unicode[STIX]{x1D70B}_{P}(\mathfrak{l}_{\unicode[STIX]{x1D703}}+\mathfrak{A}_{P})=\mathfrak{l}_{P}$
. We deduce that
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}+\mathfrak{A}_{P}$
is strictly larger than
$\mathfrak{l}_{\unicode[STIX]{x1D703}}+\mathfrak{A}_{P}$
is strictly larger than
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}$
. This contradicts the fact that
$\mathfrak{l}_{\unicode[STIX]{x1D703}}$
. This contradicts the fact that
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}$
is the largest among the ideals
$\mathfrak{l}_{\unicode[STIX]{x1D703}}$
is the largest among the ideals
![]() $\mathfrak{l}$
of
$\mathfrak{l}$
of
![]() $\mathbb{I}_{0}$
satisfying
$\mathbb{I}_{0}$
satisfying
![]() $\mathfrak{l}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})\subset \mathfrak{G}_{r}$
.◻
$\mathfrak{l}\cdot \mathfrak{s}\mathfrak{p}_{4}(\mathbb{B}_{r})\subset \mathfrak{G}_{r}$
.◻
By combining Theorem 11.4 and Lemma 11.3(ii), we obtain the following.
Corollary 11.5. When the residual representation
![]() $\overline{\unicode[STIX]{x1D70C}}$
is full, the Galois level
$\overline{\unicode[STIX]{x1D70C}}$
is full, the Galois level
![]() $\mathfrak{l}_{\unicode[STIX]{x1D703}}$
is trivial.
$\mathfrak{l}_{\unicode[STIX]{x1D703}}$
is trivial.
Acknowledgements
The results in this paper were obtained as part of the work for my Ph.D. thesis at the Laboratoire Analyse, Géométrie et Applications of Université Paris 13. I would like to thank my advisor, Jacques Tilouine, for having suggested that I work on the subject presented here and for having guided me in the preparation of the thesis. I wish to thank all the members of the équipe Arithmétique et Géométrie Algébrique of Université Paris 13 of the past three years for creating an excellent working environment. The preparation of the paper was completed while I was a postdoctoral fellow at Concordia University in Montreal. I thank Adrian Iovita for inviting me there and for his helpful suggestions. I also wish to thank Anne-Marie Aubert, Kevin Buzzard, Denis Benois, Joël Bellaïche, Huan Chen, Gaëtan Chenevier, Giovanni Di Matteo, Taiweng Deng, Mladen Dimitrov, Yiwen Ding, Haruzo Hida, Jaclyn Lang, Shinan Liu, Giovanni Rosso, Benjamin Schraen and Benoît Stroh for useful discussions. Finally, I thank the anonymous referee for his careful reading and interesting comments.