Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-03T17:51:52.378Z Has data issue: false hasContentIssue false
  • English
  • Français

RATE-ADAPTIVE BOOTSTRAP FOR POSSIBLY MISSPECIFIED GMM

Published online by Cambridge University Press:  22 January 2024

Han Hong  and
Jessie Li
Han Hong
Affiliation:
Stanford University
Jessie Li*
Affiliation:
University of California, Santa Cruz
*
Address correspondence to Jessie Li, Department of Economics, University of California, Santa Cruz, Santa Cruz, CA, USA; e-mail: jeqli@ucsc.edu.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider inference for possibly misspecified GMM models based on possibly nonsmooth moment conditions. While it is well known that misspecified GMM estimators with smooth moments remain 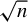$\sqrt {n}$ consistent and asymptotically normal, globally misspecified nonsmooth GMM estimators are 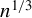$n^{1/3}$ consistent when either the weighting matrix is fixed or when the weighting matrix is estimated at the 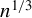$n^{1/3}$ rate or faster. Because the estimator’s nonstandard asymptotic distribution cannot be consistently estimated using the standard bootstrap, we propose an alternative rate-adaptive bootstrap procedure that consistently estimates the asymptotic distribution regardless of whether the GMM estimator is smooth or nonsmooth, correctly or incorrectly specified. Monte Carlo simulations for the smooth and nonsmooth cases confirm that our rate-adaptive bootstrap confidence intervals exhibit empirical coverage close to the nominal level.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 51
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

We thank three anonymous referees, Denis Chetverikov, Ivan Fernandez-Val, Jean-Jacques Forneron, Hiroaki Kaido, Peter Phillips, Zhongjun Qu, Yinchu Zhu, and participants in conferences and seminars for helpful comments.

References

Armstrong, T. B., & Kolesár, M. (2021). Sensitivity analysis using approximate moment condition models. Quantitative Economics , 12(1), 77–108.CrossRefGoogle Scholar
Berkowitz, D., Caner, M., & Fang, Y. (2012). The validity of instruments revisited. Journal of Econometrics , 166(2), 255–266.CrossRefGoogle Scholar
Bickel, P. J., & Freedman, D. A. (1981). Some asymptotic theory for the bootstrap. Annals of Statistics , 9(6), 1196–1217.CrossRefGoogle Scholar
Bonhomme, S., & Weidner, M. (2022). Minimizing sensitivity to model misspecification. Quantitative Economics , 13(3), 907–954.CrossRefGoogle Scholar
Brown, B. W., & Newey, W. K. (2002). Generalized method of moments, efficient bootstrapping, and improved inference. Journal of Business & Economic Statistics , 20(4), 507–517.CrossRefGoogle Scholar
Cattaneo, J., & Nagasawa, K. (2020). Bootstrap-based inference for cube root asymptotics. Econometrica , 88(5), 2203–2219.CrossRefGoogle Scholar
Cattaneo, M. D., & Jansson, M. (2018). Kernel-based semiparametric estimators: Small bandwidth asymptotics and bootstrap consistency. Econometrica , 86(3), 955–995.CrossRefGoogle Scholar
Cattaneo, M. D., & Jansson, M. (2022) Average density estimators: Efficiency and bootstrap consistency. Econometric Theory , 38(6), 1140–1174.CrossRefGoogle Scholar
Cheng, X., Liao, Z., & Shi, R. (2019). On uniform asymptotic risk of averaging GMM estimators. Quantitative Economics , 10(3), 931–979.CrossRefGoogle Scholar
Chernozhukov, V., & Hansen, C. (2005). An IV model of quantile treatment effects. Econometrica , 73(1), 245–261.CrossRefGoogle Scholar
Chernozhukov, V., & Hong, H. (2003) An MCMC approach to classical estimation. Journal of Econometrics , 115(2), 293–346.CrossRefGoogle Scholar
Creel, M., Gao, J., Hong, H., & Kristensen, D. (2015). Bayesian indirect inference and the ABC of GMM. PubMed Central. https://doi.org/10.48550/arXiv.1512.07385 CrossRefGoogle Scholar
Dudley, R. M. (1987). Universal Donsker classes and metric entropy. Annals of Probability , 15(4), 1306–1326.CrossRefGoogle Scholar
Giurcanu, M., & Presnell, B. (2018). Bootstrap inference for misspecified moment condition models. Annals of the Institute of Statistical Mathematics , 70(3), 605–630.CrossRefGoogle Scholar
Guggenberger, P. (2012). On the asymptotic size distortion of tests when instruments locally violate the exogeneity assumption. Econometric Theory , 28(2), 387–421.CrossRefGoogle Scholar
Hall, A. R., & Inoue, A. (2003). The large sample behaviour of the generalized method of moments estimator in misspecified models. Journal of Econometrics , 114(2), 361–394.CrossRefGoogle Scholar
Hall, P., & Horowitz, J. L. (1996). Bootstrap critical values for tests based on generalized-method-of-moments estimators. Econometrica , 64(4), 891–916.CrossRefGoogle Scholar
Hansen, B. E., & Lee, S. (2021). Inference for iterated GMM under misspecification. Econometrica , 89(3), 1419–1447.CrossRefGoogle Scholar
Hong, H., & Li, J. (2020). The numerical bootstrap. Annals of Statistics , 48(1), 397–412.CrossRefGoogle Scholar
Honoré, B. E., & Hu, L. (2004a). Estimation of cross sectional and panel data censored regression models with endogeneity. Journal of Econometrics , 122(2), 293–316.CrossRefGoogle Scholar
Honoré, B. E., & Hu, L. (2004b). On the performance of some robust instrumental variables estimators. Journal of Business & Economic Statistics , 22(1), 30–39.CrossRefGoogle Scholar
Jun, S. J., Pinkse, J., & Wan, Y. (2015). Classical Laplace estimation for $\sqrt[3]{\mathrm{n}}$ -consistent estimators: Improved convergence rates and rate-adaptive inference. Journal of Econometrics , 187(1), 201–216.CrossRefGoogle Scholar
Kim, J., & Pollard, D. (1990). Cube root asymptotics. Annals of Statistics , 18(1), 191–219.CrossRefGoogle Scholar
Kosorok, M. R. (2007). Introduction to empirical processes and semiparametric inference . Springer.Google Scholar
Lee, S. (2014). Asymptotic refinements of a misspecification-robust bootstrap for generalized method of moments estimators. Journal of Econometrics , 178, 398–413.CrossRefGoogle Scholar
Lehmann, E. L., & Romano, J. P. (2006). Testing statistical hypotheses . Springer Science & Business Media.Google Scholar
McFadden, D. (1989). A method of simulated moments for estimation of discrete response models without numerical integration. Econometrica , 57(5), 995–1026.CrossRefGoogle Scholar
Newey, W., & McFadden, D. (1994). Large sample estimation and hypothesis testing. In Engle, R., & McFadden, D. (Eds.), Handbook of econometrics (Vol. 4, pp. 2113–2241). North-Holland.Google Scholar
Pakes, A., & Pollard, D. (1989). Simulation and the asymptotics of optimization estimators. Econometrica , 57(5), 1027–1057.CrossRefGoogle Scholar
Phillips, P. C. B. (2015). Halbert White Jr. memorial JFEC lecture: Pitfalls and possibilities in predictive regression. Journal of Financial Econometrics , 13(3), 521–555.CrossRefGoogle Scholar
Politis, D., Romano, J., & Wolf, M. (1999). Subsampling . Springer Series in Statistics. Springer.CrossRefGoogle Scholar
Pollard, D. (1989). Asymptotics via empirical processes. Statistical Science , 4(4), 341–354.Google Scholar
Pollard, D. (1991) Asymptotics for least absolute deviation regression estimators. Econometric Theory , 7(2), 186–199.CrossRefGoogle Scholar
Serfling, R. J. (1980). Approximation theorems of mathematical statistics (Vol. 162). John Wiley & Sons.CrossRefGoogle Scholar
van der Vaart, A. W. (2000). Asymptotic statistics . Cambridge Series in Statistical and Probabilistic Mathematics (Vol. 3). Cambridge University Press).Google Scholar
van der Vaart, A. W., & Wellner, J. (1996). Weak convergence and empirical processes . Springer.CrossRefGoogle Scholar
Wellner, J. A. , & Zhan, Y. (1996). Bootstrapping Z-estimators. University of Washington Department of Statistics Technical Report, 308. Google Scholar
Zhou, Z., Mentch, L., & Hooker, G. (2021). V-statistics and variance estimation. Journal of Machine Learning Research , 22(287), 1–48.Google Scholar