Online ordering is currently unavailable due to technical issues. We apologise for any delays responding to customers while we resolve this. For further updates please visit our website: https://www.cambridge.org/news-and-insights/technical-incident
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 21 January 2009
We consider an equation with constant coefficients
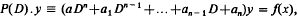
where a≠0 and f(x) is continuous in a suitable interval. Suppose that the symbolic polynomial P(D) has been fully decomposed into its (real or complex) linear factors, so that the equation may be written
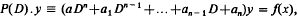
where b1, …, bq are distinct, and m1+…+mq = n. The Complementary Function being now known, we may write down a particular integral of (1) by Cauchy's method.
You have
Access
