Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-06-02T09:16:22.369Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded complexity, mean equicontinuity and discrete spectrum

Part of: Ergodic theory Topological dynamics

Published online by Cambridge University Press:  07 October 2019

WEN HUANG ,
JIAN LI Open the ORCID record for JIAN LI [Opens in a new window] ,
JEAN-PAUL THOUVENOT ,
LEIYE XU  and
XIANGDONG YE
WEN HUANG
Affiliation:
Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Sciences and Department of Mathematics, University of Science and Technology of China, Hefei, Anhui230026, China email wenh@mail.ustc.edu.cn, leoasa@mail.ustc.edu.cn, yexd@ustc.edu.cn
JIAN LI
Affiliation:
Department of Mathematics, Shantou University, Shantou, Guangdong515063, P.R. China email lijian09@mail.ustc.edu.cn
JEAN-PAUL THOUVENOT
Affiliation:
Université Paris 6-LPMA, case courrier 188, 4 place Jussieu, 75252Paris Cedex 05, France email jeanpaul.thouvenot@gmail.com
LEIYE XU
Affiliation:
Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Sciences and Department of Mathematics, University of Science and Technology of China, Hefei, Anhui230026, China email wenh@mail.ustc.edu.cn, leoasa@mail.ustc.edu.cn, yexd@ustc.edu.cn
XIANGDONG YE
Affiliation:
Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Sciences and Department of Mathematics, University of Science and Technology of China, Hefei, Anhui230026, China email wenh@mail.ustc.edu.cn, leoasa@mail.ustc.edu.cn, yexd@ustc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

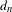We study dynamical systems that have bounded complexity with respect to three kinds metrics: the Bowen metric $d_{n}$, the max-mean metric 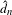$\hat{d}_{n}$ and the mean metric 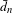$\bar{d}_{n}$, both in topological dynamics and ergodic theory. It is shown that a topological dynamical system 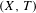$(X,T)$ has bounded complexity with respect to 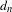$d_{n}$ (respectively 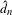$\hat{d}_{n}$) if and only if it is equicontinuous (respectively equicontinuous in the mean). However, we construct minimal systems that have bounded complexity with respect to 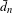$\bar{d}_{n}$ but that are not equicontinuous in the mean. It turns out that an invariant measure $\unicode[STIX]{x1D707}$ on 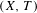$(X,T)$ has bounded complexity with respect to 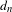$d_{n}$ if and only if 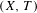$(X,T)$ is $\unicode[STIX]{x1D707}$-equicontinuous. Meanwhile, it is shown that $\unicode[STIX]{x1D707}$ has bounded complexity with respect to 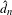$\hat{d}_{n}$ if and only if $\unicode[STIX]{x1D707}$ has bounded complexity with respect to 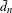$\bar{d}_{n}$, if and only if 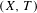$(X,T)$ is $\unicode[STIX]{x1D707}$-mean equicontinuous and if and only if it has discrete spectrum.

Keywords

bounded complexityequicontinuitymean equicontinuitydiscrete spectrum

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification
Secondary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 2 , February 2021 , pp. 494 - 533
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, J.. Mean-L-stable systems. Illinois J. Math. 3 (1959), 566–579.10.1215/ijm/1255455462CrossRefGoogle Scholar
Blanchard, F., Host, B. and Maass, A.. Topological complexity. Ergod. Th. & Dynam. Sys. 20(3) (2000), 641–662.10.1017/S0143385700000341CrossRefGoogle Scholar
Cyr, V. and Kra, B.. Nonexpansive ℤ2 -subdynamics and Nivat’s conjecture. Trans. Amer. Math. Soc. 367(9) (2015), 6487–6537.CrossRefGoogle Scholar
Cyr, V. and Kra, B.. Personal communication, 2018.Google Scholar
Dudley, R.. Real Analysis and Probability. Cambridge University Press, Cambridge, 2002.10.1017/CBO9780511755347CrossRefGoogle Scholar
Downarowicz, T.. Minimal models for noninvertible and not uniquely ergodic systems. Israel J. Math. 156 (2006), 93–110.10.1007/BF02773826CrossRefGoogle Scholar
Downarowicz, T. and Glasner, E.. Isomorphic extensions and applications. Topol. Methods Nonlinear Anal. 48 (2016), 321–338.Google Scholar
Edeko, N.. On the isomorphism problem for non-minimal transformations with discrete spectrum. Discrete Contin. Dyn. Syst. A 39(10) (2019), 6001–6021.CrossRefGoogle Scholar
Furstenberg, H.. Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601.10.2307/2372899CrossRefGoogle Scholar
Ferenczi, S.. Measure-theoretic complexity of ergodic systems. Israel J. Math. 100(1) (1997), 189–207.10.1007/BF02773640CrossRefGoogle Scholar
Fomin, S.. On dynamical systems with a purely point spectrum. Dokl. Akad. Nauk SSSR 77 (1951), 29–32 (In Russian).Google Scholar
García-Ramos, F.. A characterization of 𝜇-equicontinuity for topological dynamical systems. Proc. Amer. Math. Soc. 145(8) (2017), 3357–3368.10.1090/proc/13404CrossRefGoogle Scholar
García-Ramos, F.. Weak forms of topological and measure theoretical equicontinuity: relationships with discrete spectrum and sequence entropy. Ergod. Th. & Dynam. Sys. 37 (2017), 1211–1237.CrossRefGoogle Scholar
García-Ramos, F. and Jin, L.. Mean proximality and mean Li–Yorke chaos. Proc. Amer. Math. Soc. 145 (2017), 2959–2969.10.1090/proc/13440CrossRefGoogle Scholar
Host, B. and Kra, B.. Nilpotent Structures in Ergodic Theory (Mathematical Surveys and Monographs, 236) . American Mathematical Society, Providence, RI, 2018.10.1090/surv/236CrossRefGoogle Scholar
Host, B., Kra, B. and Maass, A.. Complexity of nilsystems and systems lacking nilfactors. J. Anal. Math. 124 (2014), 261–295.CrossRefGoogle Scholar
Huang, W., Lu, P. and Ye, X.. Measure-theoretical sensitivity and equicontinuity. Israel J. Math. 183 (2011), 233–283.10.1007/s11856-011-0049-xCrossRefGoogle Scholar
Huang, W., Wang, Z. and Ye, X.. Measure complexity and Möbius disjointness. Adv. Math. 347 (2019), 827–858.CrossRefGoogle Scholar
Huang, W. and Xu, L.. Special flow, weak mixing and complexity. Commun. Math. Stat. 7(1) (2019), 85–122.CrossRefGoogle Scholar
Huang, W., Xu, L. and Ye, X.. A minimal distal map on the torus with sub-exponential measure complexity. Ergod. Th. & Dynam. Sys. (2018), published online, doi:10.1017/etds.2018.57.Google Scholar
Katok, A.. Lyapunov exponents, entropy and the periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.CrossRefGoogle Scholar
Kornfeld, I. and Ormes, N.. Topological realizations of families of ergodic automorphisms, multitowers and orbit equivalence. Israel J. Math. 155 (2006), 335–357.10.1007/BF02773959CrossRefGoogle Scholar
Kwiatkowski, J.. Classification of non-ergodic dynamical systems with discrete spectra. Comment. Math. Prace Mat. 22 (1981), 263–274.Google Scholar
Li, J.. Measure-theoretic sensitivity via finite partitions. Nonlinearity 29 (2016), 2133–2144.CrossRefGoogle Scholar
Li, J., Tu, S. and Ye, X.. Mean equicontinuity and mean sensitivity. Ergod. Th. & Dynam. Sys. 35 (2015), 2587–2612.CrossRefGoogle Scholar
Li, J.. How chaotic is an almost mean equicontinuous system? Discrete Contin. Dyn. Syst. A 38(9) (2018), 4727–4744.CrossRefGoogle Scholar
Lindenstrauss, E. and Tsukamoto, M.. From rate distortion theory to metric mean dimension: variational principle. IEEE Trans. Inform. Theory 64(5) (2018), 3590–3609.CrossRefGoogle Scholar
Mañé, R.. Ergodic Theory and Differentiable Dynamics. Springer, Berlin, 1987.CrossRefGoogle Scholar
Oxtoby, J. C.. Ergodic sets. Bull. Amer. Math. Soc. (N.S.) 58 (1952), 116–136.10.1090/S0002-9904-1952-09580-XCrossRefGoogle Scholar
Scarpellini, B.. Stability properties of flows with pure point spectrum. J. Lond. Math. Soc. (2) 26(3) (1982), 451–464.CrossRefGoogle Scholar
Qiu, J. and Zhao, J.. A note on mean equicontinuity. J. Dynam. Differential Equations (2018), published online, doi:10.1007/s10884-018-9716-5.Google Scholar
Vershik, A., Zatitskiy, P. and Petrov, F.. Geometry and dynamics of admissible metrics in measure spaces. Cent. Eur. J. Math. 11(3) (2013), 379–400.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.10.1007/978-1-4612-5775-2CrossRefGoogle Scholar
Velozo, A. and Velozo, R.. Rate distortion theory, metric mean dimension and measure theoretic entropy. Preprint, 2017, arXiv:1707.05762.Google Scholar
Yu, T.. Measure-theoretic mean equicontinuity and bounded complexity. J. Difference Equ. 267(11) (2019), 6152–6170.10.1016/j.jde.2019.06.017CrossRefGoogle Scholar