Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-06-10T11:31:11.128Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuity of the spectrum of quasi-periodic Schrödinger operators with finitely differentiable potentials

Published online by Cambridge University Press:  06 July 2018

XIN ZHAO
XIN ZHAO*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, China email njuzhaox@126.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the spectrum of discrete quasi-periodic Schrödinger operators on 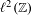$\ell ^{2}(\mathbb{Z})$ with the potentials 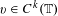$v\in C^{k}(\mathbb{T})$. For sufficiently large 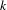$k$, we show that the Lebesgue measure of the spectrum at irrational frequencies is the limit of the Lebesgue measure of the spectrum of its periodic approximants. This gives a partial answer to the problem proposed in Jitomirskaya and Mavi [Continuity of the measure of the spectrum for quasiperiodic schrödinger operator with rough potentials. Comm. Math. Phys.325 (2014), 585–601]. Our results are based on a generalization of the rigidity theorem in Avila and Krikorian [Reducibility or non-uniform hyperbolicity for quasiperiodic Schrödinger cocycles. Ann. of Math. (2)164 (2006), 911–940]; more precisely, we prove that in the 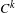$C^{k}$ case, for almost every frequency 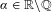$\unicode[STIX]{x1D6FC}\in \mathbb{R}\backslash \mathbb{Q}$ and for almost every 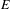$E$, the corresponding quasi-periodic Schrödinger cocycles are either reducible or non-uniformly hyperbolic.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 2 , February 2020 , pp. 564 - 576
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubry, S. and André, G.. Analyticity breaking and Anderson localization in incommensurate lattices. Ann. Israeli Phys. Soc. 3 (1980), 133–164.Google Scholar
Avila, A.. Global theory of one-frequency Schrödinger operators. Acta Math. 215 (2015), 1–54.Google Scholar
Avila, A., Fayad, B. and Krikorian, R.. A KAM scheme for SL(2, ℝ) cocycles with Liouvillean frequencies. Geom. Funct. Anal. 21 (2011), 1001–1019.Google Scholar
Avila, A. and Krikorian, R.. Reducibility or non-uniform hyperbolicity for quasiperiodic Schrödinger cocycles. Ann. of Math. (2) 164 (2006), 911–940.Google Scholar
Avila, A. and Krikorian, R.. Monotonic cocycles. Invent. Math. 202 (2015), 271–331.Google Scholar
Avron, J., Mouche, P. H. M. V. and Simon, B.. On the measure of the spectrum for the almost Mathieu operator. Comm. Math. Phys. 132 (1990), 103–118.Google Scholar
Avron, J. and Simon, B.. Almost periodic Schrödinger operators II. The integrated density of states. Duke Math. J. 50 (1983), 369–381.Google Scholar
Bjerklöv, K.. The dynamics of a class of quasi-periodic Schrödinger cocycles. Ann. Henri Poincaré 16 (2015), 961–1031.Google Scholar
Cai, A. and Ge, L.. Reducibility of finitely differentiable quasi-periodic cocycles and its spectral applications. Preprint, 2017, arXiv:1712.09041.Google Scholar
Chavaudret, C.. Strong almost reducibility for analytic and gevrey quasi-periodic cocycles. Bull. Soc. Math. France 141 (2011), 47–106.Google Scholar
Chavaudret, C.. Almost reducibility for finitely differentiable SL(2, ℝ)-valued quasi-periodic cocycles. Nonlinearity 25 (2012), 481–494.Google Scholar
Choi, M., Elliot, G. and Yui, N.. Gauss polynomials and the ratation algebra. Invent. Math. 99 (1990), 225–246.Google Scholar
Dinaburg, E. and Sinai, Ya.. The one-dimentional Schrödinger equation with a quasi-periodic potential. Funct. Anal. Appl. 9 (1975), 279–289.Google Scholar
Eliasson, L.. Floquet solutions for the 1-dimensional quasi-periodic Schrödinger equation. Commun. Math. Phys. 146 (1992), 447–482.Google Scholar
Elliot, G.. Gaps in the spectrum of an almost periodic Schrödinger operator. C. R. Math. Rep. Acad. Sci. Canada 4 (1982), 225–259.Google Scholar
Fröhlich, J., Spencer, T. and Wittwer, P.. Localization for a class of one dimensional quasi-periodic Schrödinger operators. Commun. Math. Phys. 132 (1990), 5–25.Google Scholar
Haro, A. and Puig, J.. A Thouless formular and Aubry duality for long-range Schrödinger skew-products. Nonlinearity 26 (2013), 1163–1187.Google Scholar
Herman, M.. Une méthode pour minorer les exposants de Lyapunov et quelques exemples montrant le caractère local d’un théorème d’arnol’d et de Mooser sur le tore de dimension 2. Comment. Math. Helv. 58 (1983), 453–502.Google Scholar
Hou, X. and You, J.. Almost reducibility and non-perturbative reducibility of quasiperiodic linear systems. Invent. Math. 190 (2012), 209–260.Google Scholar
Jitomirskaya, S. and Krasovsky, I.. Continuity of the measure of the spectrum for discrete quasiperiodic operators. Math. Res. Lett. 9 (2002), 413–421.Google Scholar
Jitomirskaya, S. and Last, Y.. Anderson localization for almost Mathieu operator, III. Semi-uniform localization, continuity of gaps, and the measue of the spectrum. Comm. Math. Phys. 195 (1998), 1–14.Google Scholar
Jitomirskaya, S. and Marx, C.. Analytic quasi-periodic Schrödinger operators and rational frequency approximants. Geom. Funct. Anal. 22 (2012), 1407–1443.Google Scholar
Jitomirskaya, S. and Mavi, R.. Continuity of the measure of the spectrum for quasiperiodic schrödinger operator with rough potentials. Comm. Math. Phys. 325 (2014), 585–601.Google Scholar
Johnson, R. and Moser, J.. The rotation number for almost periodic potentials. Comm. Math. Phys. 84 (1982), 403–438.Google Scholar
Last, Y.. Zero measure spectrum for the almost Mathieu operator. Comm. Math. Phys. 164 (1994), 421–432.Google Scholar
Leguil, M., You, J., Zhao, Z. and Zhou, Q.. Asymptotics of spectral gaps of quasi-periodic Schrödinger operators. Preprint, 2017, arXiv:1712.04700.Google Scholar
Moser, J. and Pöschel, J.. An extension of a result by Dinaburg and Sinai on quasi-periodic potentials. Comment. Math. Helv. 59 (1984), 39–85.Google Scholar
Puig, J.. A nonperturbative Eliasson’s reducibility theorem. Nonlinearity 19 (2006), 355–376.Google Scholar
Simon, B.. Fifteen problems in mathematical physics. Perspectives in Mathematics. Basel, Birkhäuser, 1994, pp. 423–454.Google Scholar
Simon, B.. Schrödinger operators in the twentieth century. J. Math. Phys. 41 (2000), 3523–3555.Google Scholar
Sinai, Ya.. Anderson localization for one-dimensional difference Schrödinger operator with quasi-periodic potential. J. Stat. Phys. 46 (1987), 861–909.Google Scholar
Wang, Y. and You, J.. Example of discontinuity of the Lyapunov exponent in the smooth quasi-periodic cocycles. Duke Math. J. 162 (2013), 2363–2412.Google Scholar
Wang, Y. and Zhang, Z.. Uniform positivity and continuity of Lyapunov exponents for a class of C 2 quasiperiodic Schrödinger cocycles. J. Funct. Anal. 268 (2015), 2525–2585.Google Scholar