No CrossRef data available.
Article contents
Existence and non-existence of solutions to the coboundary equation for measure-preserving systems
Published online by Cambridge University Press: 04 July 2022
Abstract
A fundamental question in the field of cohomology of dynamical systems is to determine when there are solutions to the coboundary equation:
 $$ \begin{align*} f = g - g \circ T. \end{align*} $$
$$ \begin{align*} f = g - g \circ T. \end{align*} $$
In many cases, T is given to be an ergodic invertible measure-preserving transformation on a standard probability space
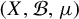 $(X, {\mathcal B}, \mu )$
and
$(X, {\mathcal B}, \mu )$
and
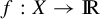 is contained in
is contained in
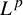 $L^p$
for
$L^p$
for
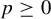 $p \geq 0$
. We extend previous results by showing for any measurable f that is non-zero on a set of positive measure, the class of measure-preserving T with a measurable solution g is meager (including the case where
$p \geq 0$
. We extend previous results by showing for any measurable f that is non-zero on a set of positive measure, the class of measure-preserving T with a measurable solution g is meager (including the case where
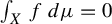 $\int _X f\,d\mu = 0$
). From this fact, a natural question arises: given f, does there always exist a solution pair T and g? In regards to this question, our main results are as follows. Given measurable f, there exist an ergodic invertible measure-preserving transformation T and measurable function g such that
$\int _X f\,d\mu = 0$
). From this fact, a natural question arises: given f, does there always exist a solution pair T and g? In regards to this question, our main results are as follows. Given measurable f, there exist an ergodic invertible measure-preserving transformation T and measurable function g such that
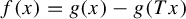 $f(x) = g(x) - g(Tx)$
for almost every (a.e.)
$f(x) = g(x) - g(Tx)$
for almost every (a.e.)
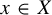 $x\in X$
, if and only if
$x\in X$
, if and only if
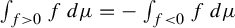 $\int _{f> 0} f\,d\mu = - \int _{f < 0} f\,d\mu $
(whether finite or
$\int _{f> 0} f\,d\mu = - \int _{f < 0} f\,d\mu $
(whether finite or
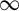 $\infty $
). Given mean-zero
$\infty $
). Given mean-zero
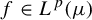 $f \in L^p(\mu )$
for
$f \in L^p(\mu )$
for
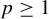 $p \geq 1$
, there exist an ergodic invertible measure-preserving T and
$p \geq 1$
, there exist an ergodic invertible measure-preserving T and
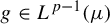 $g \in L^{p-1}(\mu )$
such that
$g \in L^{p-1}(\mu )$
such that
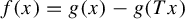 $f(x) = g(x) - g( Tx )$
for a.e.
$f(x) = g(x) - g( Tx )$
for a.e.
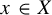 $x \in X$
. In some sense, the previous existence result is the best possible. For
$x \in X$
. In some sense, the previous existence result is the best possible. For
 $p \geq 1$
, there exists a dense
$p \geq 1$
, there exists a dense
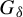 $G_{\delta }$
set of mean-zero
$G_{\delta }$
set of mean-zero
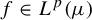 $f \in L^p(\mu )$
such that for any ergodic invertible measure-preserving T and any measurable g such that
$f \in L^p(\mu )$
such that for any ergodic invertible measure-preserving T and any measurable g such that
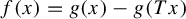 $f(x) = g(x) - g(Tx)$
almost everywhere, then
$f(x) = g(x) - g(Tx)$
almost everywhere, then
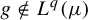 $g \notin L^q(\mu )$
for
$g \notin L^q(\mu )$
for
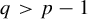 $q> p - 1$
. Finally, it is shown that we cannot expect finite moments for solutions g, when
$q> p - 1$
. Finally, it is shown that we cannot expect finite moments for solutions g, when
 $f \in L^1(\mu )$
. In particular, given any
$f \in L^1(\mu )$
. In particular, given any
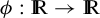 such that
such that
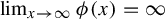 $\lim _{x\to \infty } \phi (x) = \infty $
, there exist mean-zero
$\lim _{x\to \infty } \phi (x) = \infty $
, there exist mean-zero
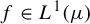 $f \in L^1(\mu )$
such that for any solutions T and g, the transfer function g satisfies:
$f \in L^1(\mu )$
such that for any solutions T and g, the transfer function g satisfies:
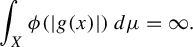 $$ \begin{align*} \int_{X} \phi ( | g(x) | )\,d\mu = \infty. \end{align*} $$
$$ \begin{align*} \int_{X} \phi ( | g(x) | )\,d\mu = \infty. \end{align*} $$
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press





