Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-06-12T00:40:42.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise equidistribution and translates of measures on homogeneous spaces

Published online by Cambridge University Press:  10 July 2018

OSAMA KHALIL
OSAMA KHALIL*
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA email khalil.37@osu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 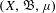$(X,\mathfrak{B},\unicode[STIX]{x1D707})$ be a Borel probability space. Let 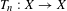$T_{n}:X\rightarrow X$ be a sequence of continuous transformations on 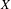$X$. Let $\unicode[STIX]{x1D708}$ be a probability measure on 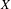$X$ such that 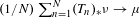$(1/N)\sum _{n=1}^{N}(T_{n})_{\ast }\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D707}$ in the weak-$\ast$ topology. Under general conditions, we show that for $\unicode[STIX]{x1D708}$ almost every 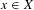$x\in X$, the measures 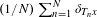$(1/N)\sum _{n=1}^{N}\unicode[STIX]{x1D6FF}_{T_{n}x}$ become equidistributed towards $\unicode[STIX]{x1D707}$ if 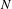$N$ is restricted to a set of full upper density. We present applications of these results to translates of closed orbits of Lie groups on homogeneous spaces. As a corollary, we prove equidistribution of exponentially sparse orbits of the horocycle flow on quotients of 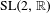$\text{SL}(2,\mathbb{R})$, starting from every point in almost every direction.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 2 , February 2020 , pp. 453 - 477
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benoist, Y. and Oh, H.. Effective equidistribution of S-integral points on symmetric varieties. Ann. Inst. Fourier (Grenoble) 62 (2012), 1889–1942.Google Scholar
Bourgain, J.. Pointwise ergodic theorems for arithmetic sets. Publ. Math. Inst. Hautes Études Sci. 69 (1989), 5–41.Google Scholar
Chaika, J. and Eskin, A.. Every flat surface is Birkhoff and Oseledets generic in almost every direction. J. Mod. Dyn. 9 (2015), 1–23.Google Scholar
Eskin, A. and McMullen, C.. Mixing, counting, and equidistribution in Lie groups. Duke Math. J. 71(07) (1993), 181–209.Google Scholar
Eskin, A., Mozes, S. and Shah, N.. Unipotent flows and counting lattice points on homogeneous varieties. Ann. of Math. (2) 143 (1996), 253–299.Google Scholar
Einsiedler, M. and Ward, T.. Ergodic Theory with a View Towards Number Theory (Graduate Texts in Mathematics, 59) . Springer, London, 2011.Google Scholar
Flaminio, L., Forni, G. and Tanis, J.. Effective equidistribution of twisted horocycle flows and horocycle maps. Geom. Funct. Anal. 26 (2016), 1359–1448.Google Scholar
Groemer, H.. On the symmetric difference metric for convex bodies. Beitr. Algebra Geom. 41 (2000), 107–114.Google Scholar
Kleinbock, D., Shi, R. and Weiss, B.. Pointwise equidistribution with an error rate and with respect to unbounded functions. Math. Ann. 367 (2017), 857–879.Google Scholar
Mozes, S.. Mixing of all orders of Lie groups actions. Invent. Math. 107 (1992), 235–242.Google Scholar
Ratner, M.. On Raghunathan’s measure conjecture. Ann. of Math. (2) 134 (1991), 545–607.Google Scholar
Schlichtkrull, H.. Hyperfunctions and Harmonic Analysis on Symmetric Spaces (Progress in Mathematics, 49) . Birkhäuser, Boston, MA, 1984.Google Scholar
Shah, N. A.. Limit distributions of polynomial trajectories on homogeneous spaces. Duke Math. J. 75(09) (1994), 711–732.Google Scholar
Shi, R.. Pointwise equidistribution for one parameter diagonalizable group action on homogeneous space. Preprint, 2014, arXiv:1405.2067.Google Scholar
Sarnak, P. and Ubis, A.. The horocycle flow at prime times. J. Math. Pures Appl. (9) 103(feb 2015) 575–618.Google Scholar
Tanis, J. and Vishe, P.. Uniform bounds for period integrals and sparse equidistribution. Int. Math. Res. Not. IMRN 2015 (2015), 13728.Google Scholar
Venkatesh, A.. Sparse equidistribution problems, period bounds and subconvexity. Ann. of Math. (2) 172 (2010), 989–1094.Google Scholar
Zheng, C.. Sparse equidistribution of unipotent orbits in finite-volume quotients of PSL(2, ℝ). J. Mod. Dyn. 10 (2016), 1–21.Google Scholar