Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-06-15T21:42:14.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and convergence of two discrete schemes for a degenerate solutal non-isothermal phase-field model

Published online by Cambridge University Press:  30 April 2009

Francisco Guillén-González  and
Juan Vicente Gutiérrez-Santacreu
Francisco Guillén-González
Affiliation:
Dpto. E.D.A.N., University of Sevilla, Aptdo. 1160, 41080 Sevilla, Spain. guillen@us.es; juanvi@us.es
Juan Vicente Gutiérrez-Santacreu
Affiliation:
Dpto. E.D.A.N., University of Sevilla, Aptdo. 1160, 41080 Sevilla, Spain. guillen@us.es; juanvi@us.es
Get access

Abstract

We analyze two numerical schemes of Euler type in time and C0 finite-element type with $\mathbb{P}_1$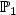-approximation in space for solving a phase-field model of a binary alloy with thermal properties. This model is written as a highly non-linear parabolic system with three unknowns: phase-field, solute concentration and temperature, where the diffusion for the temperature and solute concentration may degenerate. The first scheme is nonlinear, unconditionally stable and convergent. The other scheme is linear but conditionally stable and convergent. A maximum principle is avoided in both schemes, using a truncation operator on the L2 projection onto the $\mathbb{P}_0$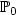 finite element for the discrete concentration. In addition, for the model when the heat conductivity and solute diffusion coefficients are constants, optimal error estimates for both schemes are shown based on stability estimates.

Keywords

Phase-field modelsdiffuse interface modelsolidification processdegenerate parabolic systemsbackward Euler schemesfinite elementsstabilityconvergenceerror estimates.
Type
Research Article
Information
ESAIM: Mathematical Modelling and Numerical Analysis , Volume 43 , Issue 3 , May 2009 , pp. 563 - 589
Copyright
© EDP Sciences, SMAI, 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boldrini, J.L. and Planas, G., Weak solutions of a phase-field model for phase change of an alloy with thermal properties. Math. Methods Appl. Sci. 25 (2002) 1177–1193. CrossRef
J.L. Boldrini and C. Vaz, A semidiscretization scheme for a phase-field type model for solidification. Port. Math. (N.S.) 63 (2006) 261–292.
S. Brenner and L.R. Scott, The Mathematical Theory of Finite Element Methods, Texts in Applied Mathathematics 15. Springer-Verlag, Berlin (1994).
Burman, E., Kessler, D. and Rappaz, J., Convergence of the finite element method applied to an anisotropic phase-field model. Ann. Math. Blaise Pascal 11 (2004) 67–94. CrossRef
Caginalp, G. and Xie, W., Phase-field and sharp-interface alloy models. Phys. Rev. E 48 (1993) 1897–1909. CrossRef
A. Ern and J.L.Guermond, Theory and practice of finite elements, Applied Mathematical Sciences 159. Springer, New York (2004).
Feng, X. and Prohl, A., Analysis of a fully discrete finite element method for the phase field model and approximation of its sharp interface limits. Math. Comp. 73 (2004) 541–567. CrossRef
Guillén-González, F. and Gutiérrez-Santacreu, J.V., Unconditional stability and convergence of a fully discrete scheme for 2D viscous fluids models with mass diffusion. Math. Comp. 77 (2008) 1495–1524 (electronic). CrossRef
O. Kavian, Introduction à la Théorie des Points Critiques, Mathématiques et Applications 13. Springer, Berlin (1993).
Kessler, D. and Scheid, J.F., A priori error estimates of a finite-element method for an isothermal phase-field model related to the solidification process of a binary alloy. IMA J. Numer. Anal. 22 (2002) 281–305. CrossRef
Rannacher, R. and Scott, R., Some optimal error estimates for piecewise linear finite element approximations. Math. Comp. 38 (1982) 437–445. CrossRef
Scheid, J.F., Global solutions to a degenerate solutal phase field model for the solidification of a binary alloy. Nonlinear Anal. 5 (2004) 207–217. CrossRef
J. Simon, Compact sets in the Space Lp(0,T;B). Ann. Mat. Pura Appl. 146 (1987) 65–97.