No CrossRef data available.
Article contents
Boolean lattices in finite alternating and symmetric groups
Published online by Cambridge University Press: 13 November 2020
Abstract
Given a group G and a subgroup H, we let 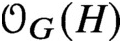 $\mathcal {O}_G(H)$ denote the lattice of subgroups of G containing H. This article provides a classification of the subgroups H of G such that
$\mathcal {O}_G(H)$ denote the lattice of subgroups of G containing H. This article provides a classification of the subgroups H of G such that 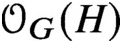 $\mathcal {O}_{G}(H)$ is Boolean of rank at least
$\mathcal {O}_{G}(H)$ is Boolean of rank at least 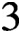 $3$ when G is a finite alternating or symmetric group. Besides some sporadic examples and some twisted versions, there are two different types of such lattices. One type arises by taking stabilisers of chains of regular partitions, and the other arises by taking stabilisers of chains of regular product structures. As an application, we prove in this case a conjecture on Boolean overgroup lattices related to the dual Ore’s theorem and to a problem of Kenneth Brown.
$3$ when G is a finite alternating or symmetric group. Besides some sporadic examples and some twisted versions, there are two different types of such lattices. One type arises by taking stabilisers of chains of regular partitions, and the other arises by taking stabilisers of chains of regular product structures. As an application, we prove in this case a conjecture on Boolean overgroup lattices related to the dual Ore’s theorem and to a problem of Kenneth Brown.
MSC classification
Information
- Type
- Algebra
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
 ${2}_2^B(q)$
and of the Ree groups
${2}_2^B(q)$
and of the Ree groups
 ${2}_2^G(q)$
’, Pacific J. Math. 240(1) (2009), 185—200.CrossRefGoogle Scholar
${2}_2^G(q)$
’, Pacific J. Math. 240(1) (2009), 185—200.CrossRefGoogle Scholar

