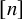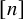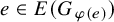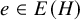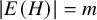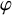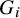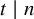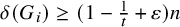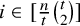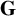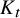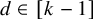1 Introduction
1.1 Rainbow extremal graph theory
A natural variant of the extremal problems concerns rainbow substructures in edge-colored graphs. From our knowledge, two types of host graphs have been studied: one class is the properly edge-colored graphs, which was first considered by Keevash et al. [Reference Janson, Łuczak and Ruciński22] – they initiated a systematic study of the rainbow Turán number, where for a fixed H and an integer n, the rainbow Turán number for H is the maximum number of edges in a properly edge-colored graph on n vertices which does not contain a rainbow H; the other class is the edge-colored multigraphs, which is equivalent to the graph system language in the Abstract, and is the main object of study in this paper. Although the two problems are different, a common scheme can be formulated as below. A k-uniform hypergraph, k-graph for short, is a pair
![]() $H=(V, E)$
, where V is a finite set of vertices and
$H=(V, E)$
, where V is a finite set of vertices and
![]() $E\subseteq \binom {V}{k}$
. We identify a hypergraph H with its edge set, writing
$E\subseteq \binom {V}{k}$
. We identify a hypergraph H with its edge set, writing
![]() $e\in H$
for
$e\in H$
for
![]() $e\in E(H)$
. We write subgraph instead of sub-k-graph or subhypergraph for brevity.
$e\in E(H)$
. We write subgraph instead of sub-k-graph or subhypergraph for brevity.
Definition 1.1. A k-graph system
![]() $\textbf {G}=\{G_1,\ldots ,G_m\}$
is a collection of not necessarily distinct k-graphs on the same vertex set V. Then a k-graph H on V is rainbow if there exists an injection
$\textbf {G}=\{G_1,\ldots ,G_m\}$
is a collection of not necessarily distinct k-graphs on the same vertex set V. Then a k-graph H on V is rainbow if there exists an injection
![]() $\varphi : E(H)\rightarrow [m]$
, such that
$\varphi : E(H)\rightarrow [m]$
, such that
![]() $e\in E(G_{\varphi (e)})$
for each
$e\in E(G_{\varphi (e)})$
for each
![]() $e\in E(H)$
.
$e\in E(H)$
.
Since
![]() $\varphi $
is an injection, it follows that all edges of H are from different members of
$\varphi $
is an injection, it follows that all edges of H are from different members of
![]() $\mathit {\mathbf {G}}$
. When
$\mathit {\mathbf {G}}$
. When
![]() $m=e(H)$
,
$m=e(H)$
,
![]() $\varphi $
is a bijection, and thus H contains exactly one edge from each
$\varphi $
is a bijection, and thus H contains exactly one edge from each
![]() $H_i$
. Note that each
$H_i$
. Note that each
![]() $G_i$
can be seen as the collection of edges with color i. Given a k-graph system
$G_i$
can be seen as the collection of edges with color i. Given a k-graph system
![]() $\mathit {\mathbf {G}}$
, the color set of a graph H, denoted by
$\mathit {\mathbf {G}}$
, the color set of a graph H, denoted by
![]() $C(H)$
, is the index set of all edges, that is
$C(H)$
, is the index set of all edges, that is
![]() $\{i:E(G_i)\cap E(H) \neq \emptyset \}$
. Note that if
$\{i:E(G_i)\cap E(H) \neq \emptyset \}$
. Note that if
![]() $|E(H)|=m$
, then a rainbow H consists of exactly one edge from each
$|E(H)|=m$
, then a rainbow H consists of exactly one edge from each
![]() $G_i$
. As for the edge-colored multigraphs, a recent breakthrough of Aharoni et al. [Reference Aharoni, DeVos, de la Maza, Montejano and Šámal2] establishes a rainbow version of the Mantel’s [Reference Pippenger and Spencer41] theorem: for
$G_i$
. As for the edge-colored multigraphs, a recent breakthrough of Aharoni et al. [Reference Aharoni, DeVos, de la Maza, Montejano and Šámal2] establishes a rainbow version of the Mantel’s [Reference Pippenger and Spencer41] theorem: for
![]() $\boldsymbol{G} =\{G_1,G_2,G_3\}$
on the same n-vertex set, if
$\boldsymbol{G} =\{G_1,G_2,G_3\}$
on the same n-vertex set, if
![]() $e(G_i)>\tau n^2$
for
$e(G_i)>\tau n^2$
for
![]() $i\in [3]$
, where
$i\in [3]$
, where
![]() $\tau \approx 0.2557$
, then
$\tau \approx 0.2557$
, then
![]() $\boldsymbol{G}$
contains a rainbow triangle. Moreover, the constant
$\boldsymbol{G}$
contains a rainbow triangle. Moreover, the constant
![]() $\tau $
is best possible. Towards a better understanding of the rainbow structures, Aharoni et al. [Reference Aharoni, DeVos, de la Maza, Montejano and Šámal2] conjectured a rainbow version of the Dirac’s [Reference Pokrovskiy42] theorem: for
$\tau $
is best possible. Towards a better understanding of the rainbow structures, Aharoni et al. [Reference Aharoni, DeVos, de la Maza, Montejano and Šámal2] conjectured a rainbow version of the Dirac’s [Reference Pokrovskiy42] theorem: for
![]() $|V|=n\geq 3$
and
$|V|=n\geq 3$
and
![]() $\mathit {\mathbf {G}}=\{G_1,\dots , G_n\}$
on V, if
$\mathit {\mathbf {G}}=\{G_1,\dots , G_n\}$
on V, if
![]() $\delta (G_i)\geq n/2$
for each
$\delta (G_i)\geq n/2$
for each
![]() $i\in [n]$
, then
$i\in [n]$
, then
![]() $\mathit {\mathbf {G}}$
contains a rainbow Hamilton cycle. This was recently verified asymptotically by Cheng et al. [Reference Cheng, Wang and Zhao9], and completely by Joos and Kim [Reference Huang, Loh and Sudakov21].
$\mathit {\mathbf {G}}$
contains a rainbow Hamilton cycle. This was recently verified asymptotically by Cheng et al. [Reference Cheng, Wang and Zhao9], and completely by Joos and Kim [Reference Huang, Loh and Sudakov21].
A natural next step is to study rainbow analogues of graph factors, which we define now. Given graphs F and G, an F-tiling is a set of vertex-disjoint copies of F in G. A perfect F-
![]() $tiling$
(or an F-factor) of G is an F-tiling covering all the vertices of G. Finding sufficient conditions for the existence of an F-factor is one of the central areas of research in extremal graph theory. The celebrated Hajnal–Szemerédi theorem reads as follows.
$tiling$
(or an F-factor) of G is an F-tiling covering all the vertices of G. Finding sufficient conditions for the existence of an F-factor is one of the central areas of research in extremal graph theory. The celebrated Hajnal–Szemerédi theorem reads as follows.
Theorem 1.2 (Hajnal–Szemerédi [Reference Frankl and Kupavskii17], Corrádi–Hajnal [Reference Corrádi and Hajnal10] for
 $t=3$
).
$t=3$
).
Every n-vertex graph G with
![]() $n\in t\mathbb {N}$
and
$n\in t\mathbb {N}$
and
![]() $\delta (G)\geq (1-\frac {1}{t})n$
has a
$\delta (G)\geq (1-\frac {1}{t})n$
has a
![]() $K_t$
-factor. Moreover, the minimum degree condition is sharp.
$K_t$
-factor. Moreover, the minimum degree condition is sharp.
A short and elegant proof was later given by Kierstead and Kostochka [Reference Keevash and Mycroft26]. The minimum degree threshold forcing an F-factor for arbitrary F was obtained by Kühn and Osthus [Reference Komlós, Sárközy and Szemerédi29, Reference Kühn, Osthus and Treglown30], improving earlier results of Alon and Yuster [Reference Alon and Yuster7] and Komlós et al. [Reference Khan27].
1.2 Our results
In this paper, we study rainbow clique-factors under a few different contexts. Our first result is an asymptotical version of the rainbow Hajnal–Szemerédi theorem.
Theorem 1.3. For every
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $t\in \mathbb N$
, there exists
$t\in \mathbb N$
, there exists
![]() $n_0\in \mathbb {N}$
, such that the following holds for all integers
$n_0\in \mathbb {N}$
, such that the following holds for all integers
![]() $n\geq n_0$
and
$n\geq n_0$
and
![]() $n\in t\mathbb {N}$
. Let
$n\in t\mathbb {N}$
. Let
![]() $m=\frac {n}{t}\binom {t}{2}$
and
$m=\frac {n}{t}\binom {t}{2}$
and
![]() $\textbf {G}=\{G_1,\ldots , G_m\}$
be an n-vertex graph system. If
$\textbf {G}=\{G_1,\ldots , G_m\}$
be an n-vertex graph system. If
![]() $\delta (G_i)\geq (1-\frac {1}{t}+\varepsilon )n$
for each i, then
$\delta (G_i)\geq (1-\frac {1}{t}+\varepsilon )n$
for each i, then
![]() $\textbf {G}$
contains a rainbow
$\textbf {G}$
contains a rainbow
![]() $K_t$
-factor.
$K_t$
-factor.
The minimum degree conditions are asymptotically best possible, as seen by setting all
![]() $G_i$
to be identical and then referring to the optimality of Theorem 1.2. In fact, this naive construction serves as a simple lower bound for all “rainbow” problems, certifying that the rainbow version is at least “as hard as” the single host graph version (although the aforementioned rainbow Mantel’s theorem says that the rainbow version can be strictly “harder”).
$G_i$
to be identical and then referring to the optimality of Theorem 1.2. In fact, this naive construction serves as a simple lower bound for all “rainbow” problems, certifying that the rainbow version is at least “as hard as” the single host graph version (although the aforementioned rainbow Mantel’s theorem says that the rainbow version can be strictly “harder”).
It is natural to seek analogues of the Hajnal–Szemerédi theorem in the digraph and oriented graph settings, where we consider factors of directed cliques, namely, tournaments. We consider digraphs with no loops and at most one edge in each direction between every pair of vertices. Let
![]() $T_k$
be the transitive tournament on k vertices, where a transitive tournament is an orientation of a complete graph D with the property that if
$T_k$
be the transitive tournament on k vertices, where a transitive tournament is an orientation of a complete graph D with the property that if
![]() $xy$
and
$xy$
and
![]() $yz$
are arcs in D with
$yz$
are arcs in D with
![]() $x\neq z$
, then the arc
$x\neq z$
, then the arc
![]() $xz$
is also in D. The minimum semidegree
$xz$
is also in D. The minimum semidegree
![]() $\delta ^0(G)$
of a digraph G is the minimum of its minimum out-degree
$\delta ^0(G)$
of a digraph G is the minimum of its minimum out-degree
![]() $\delta ^+(G)$
and its minimum in-degree
$\delta ^+(G)$
and its minimum in-degree
![]() $\delta ^-(G)$
.
$\delta ^-(G)$
.
Czygrinow et al. [Reference Czygrinow, DeBiasio, Kierstead and Molla12] proved that every digraph G on n vertices with
![]() $\delta ^+(G)\geq (1-1/k)n$
contains a perfect
$\delta ^+(G)\geq (1-1/k)n$
contains a perfect
![]() $T_k$
-tiling for integers
$T_k$
-tiling for integers
![]() $n,k$
with
$n,k$
with
![]() $k\mid n$
. Let
$k\mid n$
. Let
![]() $\mathcal {T}_k$
be the family of all tournaments on k vertices, Treglown [Reference Montgomery, Müyesser and Pehova40] proved that given an integer
$\mathcal {T}_k$
be the family of all tournaments on k vertices, Treglown [Reference Montgomery, Müyesser and Pehova40] proved that given an integer
![]() $k\geq 3$
, there exists an
$k\geq 3$
, there exists an
![]() $n_0 \in \mathbb {N}$
, such that the following holds. Suppose
$n_0 \in \mathbb {N}$
, such that the following holds. Suppose
![]() $T\in \mathcal {T}_k$
, and D is a digraph on
$T\in \mathcal {T}_k$
, and D is a digraph on
![]() $n\geq n_0$
vertices, where
$n\geq n_0$
vertices, where
![]() $k\mid n$
. If
$k\mid n$
. If
![]() $\delta ^0(D)\geq (1-1/k)n$
, then there exists a T-factor. For more results, see [Reference Czygrinow, Kierstead and Molla13, Reference Montgomery, Müyesser and Pehova40]. In this paper, we prove the following extensions of Theorem 1.3 for digraphs.
$\delta ^0(D)\geq (1-1/k)n$
, then there exists a T-factor. For more results, see [Reference Czygrinow, Kierstead and Molla13, Reference Montgomery, Müyesser and Pehova40]. In this paper, we prove the following extensions of Theorem 1.3 for digraphs.
Theorem 1.4. For every integer
![]() $k\ge 3$
and real
$k\ge 3$
and real
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $n_0\in \mathbb {N}$
, such that the following holds for all integers
$n_0\in \mathbb {N}$
, such that the following holds for all integers
![]() $n\geq n_0$
and
$n\geq n_0$
and
![]() $n\in k\mathbb {N}$
. If
$n\in k\mathbb {N}$
. If
![]() $\textbf {D}=\{D_1,\ldots ,D_m\}$
,
$\textbf {D}=\{D_1,\ldots ,D_m\}$
,
![]() $m=\frac {n}{k}\binom {k}{2}$
, is a collection of n-vertex digraphs on the same vertex set such that
$m=\frac {n}{k}\binom {k}{2}$
, is a collection of n-vertex digraphs on the same vertex set such that
![]() $\delta ^+(D_i)\geq (1-\frac {1}{k}+\varepsilon )n$
, then
$\delta ^+(D_i)\geq (1-\frac {1}{k}+\varepsilon )n$
, then
![]() $\textbf {D}$
contains a rainbow
$\textbf {D}$
contains a rainbow
![]() $T_k$
-factor.
$T_k$
-factor.
Theorem 1.5. For every integer
![]() $k\ge 3$
,
$k\ge 3$
,
![]() $T\in \mathcal {T}_k$
, and real
$T\in \mathcal {T}_k$
, and real
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $n_0 \in \mathbb {N}$
, such that the following holds for all integers
$n_0 \in \mathbb {N}$
, such that the following holds for all integers
![]() $n\geq n_0$
and
$n\geq n_0$
and
![]() $n\in k\mathbb {N}$
. If
$n\in k\mathbb {N}$
. If
![]() $\textbf {D}=\{D_1,\ldots ,D_m\}$
,
$\textbf {D}=\{D_1,\ldots ,D_m\}$
,
![]() $m=\frac {n}{k}\binom {k}{2}$
, is a collection of n-vertex digraphs on the same vertex set such that
$m=\frac {n}{k}\binom {k}{2}$
, is a collection of n-vertex digraphs on the same vertex set such that
![]() $\delta ^0(D_i)\geq (1-\frac {1}{k}+\varepsilon )n$
, then
$\delta ^0(D_i)\geq (1-\frac {1}{k}+\varepsilon )n$
, then
![]() $\textbf {D}$
contains a rainbow T-factor.
$\textbf {D}$
contains a rainbow T-factor.
We next discuss the partite setting. Suppose
![]() $V_1,\ldots , V_k$
are disjoint vertex sets each of order n, and G is a k-partite graph on vertex classes
$V_1,\ldots , V_k$
are disjoint vertex sets each of order n, and G is a k-partite graph on vertex classes
![]() $V_1,\ldots , V_k$
(that is, G is a graph on the vertex set
$V_1,\ldots , V_k$
(that is, G is a graph on the vertex set
![]() $V_1\cup \cdots \cup V_k$
, such that no edge of G has both end vertices in the same class). We define the partite minimum degree of G, denoted by
$V_1\cup \cdots \cup V_k$
, such that no edge of G has both end vertices in the same class). We define the partite minimum degree of G, denoted by
![]() $\delta '(G)$
, to be the largest m such that every vertex has at least m neighbors in each part other than its own, that is
$\delta '(G)$
, to be the largest m such that every vertex has at least m neighbors in each part other than its own, that is
where
![]() $N(v)$
denotes the neighborhood of v. Fischer [Reference Dirac15] conjectured that if
$N(v)$
denotes the neighborhood of v. Fischer [Reference Dirac15] conjectured that if
![]() $\delta '(G)\geq (1-1/k)n$
, then G has a
$\delta '(G)\geq (1-1/k)n$
, then G has a
![]() $K_k$
-factor. Recently, an approximate version of this conjecture assuming the degree condition
$K_k$
-factor. Recently, an approximate version of this conjecture assuming the degree condition
![]() $\delta '(G)\geq (1-1/k+o(1))n$
was proved independently by Keevash and Mycroft [Reference Joos and Kim23], and by Lo and Markström [Reference Kühn and Outhus32] (a corrected exact version was given by Keevash and Mycroft [Reference Keevash, Mubayi, Sudakov and Verstraëte24], in fact, they obtain a more general result for r-partite graphs with
$\delta '(G)\geq (1-1/k+o(1))n$
was proved independently by Keevash and Mycroft [Reference Joos and Kim23], and by Lo and Markström [Reference Kühn and Outhus32] (a corrected exact version was given by Keevash and Mycroft [Reference Keevash, Mubayi, Sudakov and Verstraëte24], in fact, they obtain a more general result for r-partite graphs with
![]() $r\ge k$
). We extend this approximate version to the rainbow setting.
$r\ge k$
). We extend this approximate version to the rainbow setting.
Theorem 1.6. For every
![]() $\varepsilon>0$
and integer k, there exists
$\varepsilon>0$
and integer k, there exists
![]() $n_0\in \mathbb {N}$
, such that the following holds for all integers
$n_0\in \mathbb {N}$
, such that the following holds for all integers
![]() $n\geq n_0$
. If
$n\geq n_0$
. If
![]() $\textbf {G}=\{G_1,\ldots ,G_{n\binom {k}{2}}\}$
is a collection of k-partite graphs with a common partition
$\textbf {G}=\{G_1,\ldots ,G_{n\binom {k}{2}}\}$
is a collection of k-partite graphs with a common partition
![]() $V_1,\ldots ,V_k$
each of size n, such that
$V_1,\ldots ,V_k$
each of size n, such that
![]() $\delta '(G_i)\geq (1-\frac {1}{k}+\varepsilon )n$
, then
$\delta '(G_i)\geq (1-\frac {1}{k}+\varepsilon )n$
, then
![]() $\textbf {G}$
contains a rainbow
$\textbf {G}$
contains a rainbow
![]() $K_k$
-factor.
$K_k$
-factor.
A matching in H is a collection of vertex-disjoint edges of H. A perfect matching in H is a matching that covers all vertices of H. Given
![]() $d\in [k-1]$
, the minimum d-degree of a k-graph H, denoted by
$d\in [k-1]$
, the minimum d-degree of a k-graph H, denoted by
![]() $\delta _d(H)$
, is defined as the minimum of
$\delta _d(H)$
, is defined as the minimum of
![]() $d_H(S)$
over all d-sets S of
$d_H(S)$
over all d-sets S of
![]() $V(H)$
, where
$V(H)$
, where
![]() $d_H(S)$
denotes the number of edges containing S. Another main result of this paper is to settle the rainbow version of minimum d-degree-type results for perfect matchings in k-graphs for all
$d_H(S)$
denotes the number of edges containing S. Another main result of this paper is to settle the rainbow version of minimum d-degree-type results for perfect matchings in k-graphs for all
![]() $d\in [k-1]$
, in a sense that the minimum d-degree condition which forces a perfect matching in a single k-graph is essentially sufficient to force a rainbow perfect matching in a k-graph system. Note that Joos and Kim [Reference Huang, Loh and Sudakov21] proved that
$d\in [k-1]$
, in a sense that the minimum d-degree condition which forces a perfect matching in a single k-graph is essentially sufficient to force a rainbow perfect matching in a k-graph system. Note that Joos and Kim [Reference Huang, Loh and Sudakov21] proved that
![]() $\delta (G_i)\geq n/2$
guarantees a rainbow perfect matching in an n-vertex graph system.
$\delta (G_i)\geq n/2$
guarantees a rainbow perfect matching in an n-vertex graph system.
It is well-known that perfect matchings are closely related to its fractional counterpart. Given a k-graph H, a fractional matching is a function
![]() $f: E(H)\to [0,1]$
, subject to the requirement that
$f: E(H)\to [0,1]$
, subject to the requirement that
![]() $\sum _{e:v\in e}f(e)\le 1$
, for every
$\sum _{e:v\in e}f(e)\le 1$
, for every
![]() $v\in V(H)$
. Furthermore, if equality holds for every
$v\in V(H)$
. Furthermore, if equality holds for every
![]() $v\in V(H)$
, then we call the fractional matching perfect. Denote the maximum size of a fractional matching of H by
$v\in V(H)$
, then we call the fractional matching perfect. Denote the maximum size of a fractional matching of H by
![]() $\nu ^*(H)=\max _f \Sigma _{e\in E(H)} f(e)$
. Let
$\nu ^*(H)=\max _f \Sigma _{e\in E(H)} f(e)$
. Let
![]() $c_{k,d}$
be the minimum d-degree threshold for perfect fractional matchings in k-graphs, namely, for every
$c_{k,d}$
be the minimum d-degree threshold for perfect fractional matchings in k-graphs, namely, for every
![]() $\varepsilon>0$
and sufficiently large
$\varepsilon>0$
and sufficiently large
![]() $n\in \mathbb N$
, every n-vertex k-graph H with
$n\in \mathbb N$
, every n-vertex k-graph H with
![]() $\delta _d(H)\ge (c_{k,d}+\varepsilon )\binom {n-d}{k-d}$
contains a perfect fractional matching. It is known that [Reference Alon, Frankl, Huang, Rödl, Ruciński and Sudakov5] every n-vertex k-graph H with
$\delta _d(H)\ge (c_{k,d}+\varepsilon )\binom {n-d}{k-d}$
contains a perfect fractional matching. It is known that [Reference Alon, Frankl, Huang, Rödl, Ruciński and Sudakov5] every n-vertex k-graph H with
![]() $\delta _d(H)\ge (\max \{c_{k,d}, 1/2\}+o(1))\binom {n-d}{k-d}$
has a perfect matching, and this condition is asymptotically best possible. However, determining the parameter
$\delta _d(H)\ge (\max \{c_{k,d}, 1/2\}+o(1))\binom {n-d}{k-d}$
has a perfect matching, and this condition is asymptotically best possible. However, determining the parameter
![]() $c_{k,d}$
is a major open problem in this field, and we refer to [Reference Fischer16] for related results and discussions.
$c_{k,d}$
is a major open problem in this field, and we refer to [Reference Fischer16] for related results and discussions.
Theorem 1.7. For every
![]() $\varepsilon>0$
and integer
$\varepsilon>0$
and integer
![]() $d\in [k-1]$
, there exists
$d\in [k-1]$
, there exists
![]() $n_0\in \mathbb N$
, such that the following holds for all integers
$n_0\in \mathbb N$
, such that the following holds for all integers
![]() $n\geq n_0$
and
$n\geq n_0$
and
![]() $n\in k\mathbb {N}$
. Every n-vertex k-graph system
$n\in k\mathbb {N}$
. Every n-vertex k-graph system
![]() $\textbf {G}=\{G_1, \dots , G_{\frac {n}{k}}\}$
with
$\textbf {G}=\{G_1, \dots , G_{\frac {n}{k}}\}$
with
![]() $\delta _d(G_i)\geq (\max \{c_{k,d}, \frac {1}{2}\}+\varepsilon )\binom {n-d}{k-d}$
for each i contains a rainbow perfect matching.
$\delta _d(G_i)\geq (\max \{c_{k,d}, \frac {1}{2}\}+\varepsilon )\binom {n-d}{k-d}$
for each i contains a rainbow perfect matching.
Related work. Aharoni and Howard [Reference Aharoni and Howard3] conjectured that given an n-vertex k-graph system
![]() ${\boldsymbol{G}=\{G_1,\ldots ,G_m\}}$
, if
${\boldsymbol{G}=\{G_1,\ldots ,G_m\}}$
, if
![]() $e(G_i)>\max \{\binom {n}{k}-\binom {n-m+1}{k},\binom {km-1}{k}\}$
for
$e(G_i)>\max \{\binom {n}{k}-\binom {n-m+1}{k},\binom {km-1}{k}\}$
for
![]() $i\in [m]$
, then
$i\in [m]$
, then
![]() $\boldsymbol{G}$
contains a rainbow matching of size m. The conjecture is known for
$\boldsymbol{G}$
contains a rainbow matching of size m. The conjecture is known for
![]() $n>3k^2m$
by a result of Huang et al. [Reference Hajnal and Szemerédi19], and for
$n>3k^2m$
by a result of Huang et al. [Reference Hajnal and Szemerédi19], and for
![]() $m<n/(2k)$
and sufficiently large n by a recent result of Lu et al. [Reference Lo and Markström34]. For the case
$m<n/(2k)$
and sufficiently large n by a recent result of Lu et al. [Reference Lo and Markström34]. For the case
![]() $k=3$
, Lu et al. [Reference Lu, Wang and Yu36] showed that for sufficiently large
$k=3$
, Lu et al. [Reference Lu, Wang and Yu36] showed that for sufficiently large
![]() $n\in 3\mathbb {N}$
, given a
$n\in 3\mathbb {N}$
, given a
![]() $3$
-graph system
$3$
-graph system
![]() $\boldsymbol{G}=\{G_1,\ldots ,G_{n/3}\}$
, if
$\boldsymbol{G}=\{G_1,\ldots ,G_{n/3}\}$
, if
![]() $\delta _1(G_i)>\binom {n-1}{2}-\binom {2n/3}{2}$
for
$\delta _1(G_i)>\binom {n-1}{2}-\binom {2n/3}{2}$
for
![]() $i\in [n/3]$
, then
$i\in [n/3]$
, then
![]() $\boldsymbol{G}$
contains a rainbow perfect matching (note that the single host 3-graph case was proved by Kühn et al. [Reference Kierstead and Kostochka28] and independently by Khan [Reference Keevash and Mycroft25]).
$\boldsymbol{G}$
contains a rainbow perfect matching (note that the single host 3-graph case was proved by Kühn et al. [Reference Kierstead and Kostochka28] and independently by Khan [Reference Keevash and Mycroft25]).
On a slightly different setup, Huang et al. [Reference Frankl and Rodl18] obtained a generalization of the Erdős Matching Conjecture to properly colored k-graph systems
![]() $\mathit {\mathbf {G}}$
and verified it for
$\mathit {\mathbf {G}}$
and verified it for
![]() $n\geq 3k^2m$
, where
$n\geq 3k^2m$
, where
![]() $\boldsymbol{G}=\{G_1,\ldots ,G_m\}$
and each
$\boldsymbol{G}=\{G_1,\ldots ,G_m\}$
and each
![]() $G_i$
is an n-vertex properly colored k-graph. For general F-factors, Coulson et al. [Reference Coulson, Keevash, Perarnau and Yepremyan11] proved that essentially the minimum d-degree threshold guaranteeing an F-factor in a single k-graph also forces a rainbow F-factor in any edge-coloring of G that satisfies certain natural local conditions. We refer the reader to [Reference Aharoni, Briggs, Holzman and Jiang1, Reference Aharoni and Howard4, Reference Barát, Gyárfás and Sárközy8, Reference Drisko14, Reference Kühn and Outhus31, Reference Kupavskii33, Reference Lu, Wang and Yu35, Reference Lu, Yu and Yuan38] for more results.
$G_i$
is an n-vertex properly colored k-graph. For general F-factors, Coulson et al. [Reference Coulson, Keevash, Perarnau and Yepremyan11] proved that essentially the minimum d-degree threshold guaranteeing an F-factor in a single k-graph also forces a rainbow F-factor in any edge-coloring of G that satisfies certain natural local conditions. We refer the reader to [Reference Aharoni, Briggs, Holzman and Jiang1, Reference Aharoni and Howard4, Reference Barát, Gyárfás and Sárközy8, Reference Drisko14, Reference Kühn and Outhus31, Reference Kupavskii33, Reference Lu, Wang and Yu35, Reference Lu, Yu and Yuan38] for more results.
2 Proof ideas and a general framework for rainbow F-factors
Our proof is under the framework of the absorption method, pioneered by Rödlet al. [Reference Mantel39], which reduces the problem of finding a spanning subgraph to building an absorption structure and an almost spanning structure. Tailored to our problem, the naive idea is to build a rainbow absorption structure and a rainbow almost F-factor. Moreover, the rainbow absorption structure must be able to deal with (i.e., absorb) an arbitrary leftover of vertices, as well as a leftover of colors.
2.1 A general framework for rainbow F-factors
To state our general theorem for rainbow F-factors, we need some general notation that captures all of our contexts. We shall consider a directed k-graph (Dk-graph) H, with edge set
![]() $E(H)\subseteq \binom {V(H)}k\times \{+, -\}$
, that is, each edge consists of k vertices and a direction taken from
$E(H)\subseteq \binom {V(H)}k\times \{+, -\}$
, that is, each edge consists of k vertices and a direction taken from
![]() $\{+, -\}$
. This way, a directed (
$\{+, -\}$
. This way, a directed (
![]() $2$
-)graph can be recognized as a graph with an ordered vertex set, and edges following (or against) the order of the enumeration are oriented by
$2$
-)graph can be recognized as a graph with an ordered vertex set, and edges following (or against) the order of the enumeration are oriented by
![]() $+$
(or
$+$
(or
![]() $-$
).
$-$
).
Given a Dk-graph
![]() $H=(V,E)$
, for
$H=(V,E)$
, for
![]() $E'\subseteq E$
, we write
$E'\subseteq E$
, we write
![]() $H[E']$
for the subgraph of H with edge set
$H[E']$
for the subgraph of H with edge set
![]() $E'$
and vertex set
$E'$
and vertex set
![]() $\cup _{e\in E'} E'$
. For
$\cup _{e\in E'} E'$
. For
![]() $V'\subseteq V$
, if
$V'\subseteq V$
, if
![]() $H'\subseteq H$
contains all edges of H with vertices in
$H'\subseteq H$
contains all edges of H with vertices in
![]() $V'$
, then
$V'$
, then
![]() $H'$
is an induced subgraph of H. Denote it by
$H'$
is an induced subgraph of H. Denote it by
![]() $H[V']$
. If there is an F-tiling in H whose vertex set is
$H[V']$
. If there is an F-tiling in H whose vertex set is
![]() $V'$
, then we say that
$V'$
, then we say that
![]() $V'$
spans an F-tiling. Given another Dk-graph
$V'$
spans an F-tiling. Given another Dk-graph
![]() $H_1=(V_1,E_1)$
, we set
$H_1=(V_1,E_1)$
, we set
![]() $H\cup H_1:= (V\cup V_1, E\cup E_1)$
.
$H\cup H_1:= (V\cup V_1, E\cup E_1)$
.
Given a Dk-graph F with b vertices and f edges, a Dk-graph system
![]() $\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{\frac {n}{b}f}\}$
on vertex V and a subset
$\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{\frac {n}{b}f}\}$
on vertex V and a subset
![]() $V'\subseteq V$
. Let
$V'\subseteq V$
. Let
![]() $\mathit {\mathbf {G}}[V']=\{G_1[V'], \ldots , G_{\frac {n}{b}f}[V']\}$
be the induced Dk-graph system on
$\mathit {\mathbf {G}}[V']=\{G_1[V'], \ldots , G_{\frac {n}{b}f}[V']\}$
be the induced Dk-graph system on
![]() $V'$
. If
$V'$
. If
![]() $|V'|\in b\mathbb {N}$
and there exists a rainbow perfect F-tiling inside
$|V'|\in b\mathbb {N}$
and there exists a rainbow perfect F-tiling inside
![]() $\mathit {\mathbf {G}}[V']$
whose color set is
$\mathit {\mathbf {G}}[V']$
whose color set is
![]() $C\subseteq [nf/b]$
, then we say that
$C\subseteq [nf/b]$
, then we say that
![]() $V'$
spans a rainbow F-tiling in
$V'$
spans a rainbow F-tiling in
![]() $\mathit {\mathbf {G}}$
with color set C. Let
$\mathit {\mathbf {G}}$
with color set C. Let
![]() $A_1$
and
$A_1$
and
![]() $A_2$
be two rainbow Dk-graphs in
$A_2$
be two rainbow Dk-graphs in
![]() $\mathit {\mathbf {G}}$
with color set
$\mathit {\mathbf {G}}$
with color set
![]() $C_1$
and
$C_1$
and
![]() $C_2$
, respectively, we set
$C_2$
, respectively, we set
![]() $A_1\cup A_2$
to be a Dk-graph with vertex set
$A_1\cup A_2$
to be a Dk-graph with vertex set
![]() $V(A_1)\cup V(A_2)$
, edge set
$V(A_1)\cup V(A_2)$
, edge set
![]() $E(A_1)\cup E(A_2)$
, and color set
$E(A_1)\cup E(A_2)$
, and color set
![]() $C_1\cup C_2$
. The following general minimum degree condition captures all of our contexts.
$C_1\cup C_2$
. The following general minimum degree condition captures all of our contexts.
Definition 2.1. Let H be a Dk-graph and
![]() $d\in [k-1]$
, a minimum d-degree
$d\in [k-1]$
, a minimum d-degree
![]() $\delta ^*_d(H)$
corresponding to a certain (implicit) degree rule can be defined as follows. There exists
$\delta ^*_d(H)$
corresponding to a certain (implicit) degree rule can be defined as follows. There exists
![]() $\ell \in \mathbb {N}$
, such that for any d-set
$\ell \in \mathbb {N}$
, such that for any d-set
![]() $S\subseteq V(H)$
, let
$S\subseteq V(H)$
, let
where
![]() $E_i$
is a set of edges of H that each contains S as a subset. Let
$E_i$
is a set of edges of H that each contains S as a subset. Let
![]() $\deg ^*(S):=\min _{i\in [\ell ]}|E_i|$
and
$\deg ^*(S):=\min _{i\in [\ell ]}|E_i|$
and
![]() $\delta ^*_d(H):=\min _{S\subseteq \binom {V}{d}}\deg ^*(S)$
.
$\delta ^*_d(H):=\min _{S\subseteq \binom {V}{d}}\deg ^*(S)$
.
We list all the instances of minimum degrees used in this paper.
-
• When H is a k-graph, we can take
 $\ell =1$
and
$\ell =1$
and
 $E_1$
as all edges containing S, thus
$E_1$
as all edges containing S, thus
 $\deg ^*(S)=|E_1|$
and
$\deg ^*(S)=|E_1|$
and
 $\delta ^*_d(H)$
represents the standard minimum d-degree of H.
$\delta ^*_d(H)$
represents the standard minimum d-degree of H. -
• When H is a k-partite 2-graph, we can take
 $\ell =k-1$
, where
$\ell =k-1$
, where
 $E_i$
consists of the edges from
$E_i$
consists of the edges from
 $S=\{v\}$
to
$S=\{v\}$
to
 $V_i$
for
$V_i$
for
 $i\in [k]\setminus \{j:v\in V_j\}$
, thus
$i\in [k]\setminus \{j:v\in V_j\}$
, thus
 $\deg ^*(S)=\min \{|E_i|:i\in [k]\setminus \{j:v\in V_j\}\}$
and
$\deg ^*(S)=\min \{|E_i|:i\in [k]\setminus \{j:v\in V_j\}\}$
and
 $\delta ^*_1(H)$
represents the minimum partite degree of H.
$\delta ^*_1(H)$
represents the minimum partite degree of H. -
• When H is a directed graph and
 $S=\{v\}$
for a given vertex v, we can take
$S=\{v\}$
for a given vertex v, we can take
 $\ell =1$
and take
$\ell =1$
and take
 $E_1$
as the sets of out(in)-edges, thus,
$E_1$
as the sets of out(in)-edges, thus,
 $\deg ^*(S)=|E_1|$
and
$\deg ^*(S)=|E_1|$
and
 $\delta ^*_1(H)$
represents the minimum out(in)-degree of H.
$\delta ^*_1(H)$
represents the minimum out(in)-degree of H. -
• When H is a directed graph and
 $S=\{v\}$
for a given vertex v, we can take
$S=\{v\}$
for a given vertex v, we can take
 $\ell =2$
and take
$\ell =2$
and take
 $E_1, E_2$
as the sets of in-edges and out-edges, respectively, thus,
$E_1, E_2$
as the sets of in-edges and out-edges, respectively, thus,
 $\deg ^*(S)=\min \{|E_1|,|E_2|\}$
and
$\deg ^*(S)=\min \{|E_1|,|E_2|\}$
and
 $\delta ^*_1(H)$
represents the minimum semidegree of H.
$\delta ^*_1(H)$
represents the minimum semidegree of H.
Throughout the rest of this paper, let F be a Dk-graph with b vertices and f edges. We first define an absorber without colors. Given a set B of b vertices, a Dk-graph
![]() $A^0=A_1^0\cup A_2^0$
is called an F-absorber for B if
$A^0=A_1^0\cup A_2^0$
is called an F-absorber for B if
-
•
 $V(A^0)=B\dot \cup L$
Footnote
1
,
$V(A^0)=B\dot \cup L$
Footnote
1
, -
•
 $A_1^0$
is an F-factor on L, and
$A_1^0$
is an F-factor on L, and
 $A_2^0$
is an F-factor on
$A_2^0$
is an F-factor on
 $B\cup L$
.
$B\cup L$
.
Note that
![]() $|V(A^0)|$
is always a constant in this paper. Naturally, we give the definition of rainbow F-absorber as follows.
$|V(A^0)|$
is always a constant in this paper. Naturally, we give the definition of rainbow F-absorber as follows.
Definition 2.2 (Rainbow F-absorber).
Let
![]() $\textbf G=\{G_1,\dots , G_{nf/b}\}$
be a Dk-graph system on V and F be a Dk-graph with b vertices and f edges. For every b-set B in V and every f-set C in
$\textbf G=\{G_1,\dots , G_{nf/b}\}$
be a Dk-graph system on V and F be a Dk-graph with b vertices and f edges. For every b-set B in V and every f-set C in
![]() $[nf/b]$
,
$[nf/b]$
,
![]() $A=A_1\cup A_2$
is called a rainbow F-absorber for
$A=A_1\cup A_2$
is called a rainbow F-absorber for
![]() $(B,C)$
if
$(B,C)$
if
-
•
 $V(A)=B\dot \cup L$
,
$V(A)=B\dot \cup L$
, -
•
 $A_1$
is a rainbow F-factor on L with color set
$A_1$
is a rainbow F-factor on L with color set
 $C_1$
, and
$C_1$
, and
 $A_2$
is a rainbow F-factor on
$A_2$
is a rainbow F-factor on
 $B\cup L$
with color set
$B\cup L$
with color set
 $C_1\cup C$
.
$C_1\cup C$
.
A rainbow F-absorber for
![]() $(B, C)$
works in the following way:
$(B, C)$
works in the following way:
![]() $A_1$
is a rainbow F-tiling with color set
$A_1$
is a rainbow F-tiling with color set
![]() $C_1$
, thus, if the vertices of B and the colors C are available, then we can switch to
$C_1$
, thus, if the vertices of B and the colors C are available, then we can switch to
![]() $A_2$
and get a larger rainbow F-tiling. For example (see Figure 1), let
$A_2$
and get a larger rainbow F-tiling. For example (see Figure 1), let
![]() $\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{n}\}$
be a graph system on n-vertex set V. For any
$\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{n}\}$
be a graph system on n-vertex set V. For any
![]() $B=\{v_1,v_2,v_3\}$
and
$B=\{v_1,v_2,v_3\}$
and
![]() $C=\{i,j,k\}$
, we construct a rainbow triangle-absorber A for
$C=\{i,j,k\}$
, we construct a rainbow triangle-absorber A for
![]() $(B,C)$
, where
$(B,C)$
, where
![]() $V(A)=B\cup \{v_4,\ldots ,v_{12}\}$
.
$V(A)=B\cup \{v_4,\ldots ,v_{12}\}$
.
![]() $\{v_4v_7v_8,v_5v_9v_{10},v_6v_{11}v_{12}\}$
is a family of rainbow triangles with color set
$\{v_4v_7v_8,v_5v_9v_{10},v_6v_{11}v_{12}\}$
is a family of rainbow triangles with color set
![]() $C_1$
, which serves as
$C_1$
, which serves as
![]() $A_1$
.
$A_1$
.
![]() $\{v_1v_7v_8,v_2v_9v_{10},v_3v_{11}v_{12},v_4v_5v_6\}$
is a family of rainbow triangles with color set
$\{v_1v_7v_8,v_2v_9v_{10},v_3v_{11}v_{12},v_4v_5v_6\}$
is a family of rainbow triangles with color set
![]() $C_1\cup \{i,j,k\}$
, which serves as
$C_1\cup \{i,j,k\}$
, which serves as
![]() $A_2$
. Now we introduce one of the main parameters
$A_2$
. Now we introduce one of the main parameters
![]() $c_{d,F}^{\mathrm {abs,*}}$
. Roughly speaking, it is the minimum degree threshold, such that all b-sets are contained in many rainbow F-absorbers.
$c_{d,F}^{\mathrm {abs,*}}$
. Roughly speaking, it is the minimum degree threshold, such that all b-sets are contained in many rainbow F-absorbers.
Definition 2.3 (
 $c_{d,F}^{\mathrm {abs,*}}$
: Rainbow absorption threshold).
$c_{d,F}^{\mathrm {abs,*}}$
: Rainbow absorption threshold).
Fix an F-absorber
![]() $A^0=A^0_1\cup A^0_2$
, and let m be the number of vertex disjoint copies of F in
$A^0=A^0_1\cup A^0_2$
, and let m be the number of vertex disjoint copies of F in
![]() $A^0_2$
. Let
$A^0_2$
. Let
![]() $c_{d,F,A^0}\in (0,1)$
be the infimum of reals
$c_{d,F,A^0}\in (0,1)$
be the infimum of reals
![]() $c>0$
, such that for every
$c>0$
, such that for every
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $\varepsilon '>0$
, such that the following holds for sufficiently large
$\varepsilon '>0$
, such that the following holds for sufficiently large
![]() $n\in \mathbb {N}$
, where
$n\in \mathbb {N}$
, where
![]() $d\in [k-1]$
. Let
$d\in [k-1]$
. Let
![]() $\textbf G=\{G_1,\dots , G_{nf/b}\}$
be an n-vertex Dk-graph system on V. If
$\textbf G=\{G_1,\dots , G_{nf/b}\}$
be an n-vertex Dk-graph system on V. If
![]() $\delta _d^*(G_i)\ge (c+\varepsilon )\binom {n-d}{k-d}$
for
$\delta _d^*(G_i)\ge (c+\varepsilon )\binom {n-d}{k-d}$
for
![]() $i\in [nf/b]$
, then for every b-set B in V and every f-set C in
$i\in [nf/b]$
, then for every b-set B in V and every f-set C in
![]() $[nf/b]$
with the form
$[nf/b]$
with the form
![]() $[(i-1)f,if]$
for some
$[(i-1)f,if]$
for some
![]() $i\in [n/b]$
, there are at least
$i\in [n/b]$
, there are at least
![]() $\varepsilon ' n^{(m-1)(b+1)}$
rainbow F-absorbers A with color set
$\varepsilon ' n^{(m-1)(b+1)}$
rainbow F-absorbers A with color set
![]() $C(A_1^0)\cup C$
whose underlying graph is isomorphic to
$C(A_1^0)\cup C$
whose underlying graph is isomorphic to
![]() $A^0$
, such that
$A^0$
, such that
![]() $C(A_1^0)=[(i_1-1)f+1,i_1f]\cup [(i_2-1)f+1,i_2f]\cup \cdots \cup [(i_{m-1}-1)f+1,i_{m-1}f]$
, where
$C(A_1^0)=[(i_1-1)f+1,i_1f]\cup [(i_2-1)f+1,i_2f]\cup \cdots \cup [(i_{m-1}-1)f+1,i_{m-1}f]$
, where
![]() $i_j\in [n/b]$
for each
$i_j\in [n/b]$
for each
![]() $j\in [m-1]$
and
$j\in [m-1]$
and
![]() $i_{j_1}\neq i_{j_2}$
for distinct
$i_{j_1}\neq i_{j_2}$
for distinct
![]() $j_1,j_2\in [m-1]$
. Let
$j_1,j_2\in [m-1]$
. Let
![]() $c_{d,F}^{\mathrm {abs,*}}:=\inf c_{d,F,A^0}$
, where the infimum is over all F-absorbers
$c_{d,F}^{\mathrm {abs,*}}:=\inf c_{d,F,A^0}$
, where the infimum is over all F-absorbers
![]() $A^0$
.
$A^0$
.

Figure 1 A rainbow triangle-absorber A for
![]() $(B,C)$
.
$(B,C)$
.
We next define a threshold parameter for the rainbow almost F-factor in a similar fashion. We use the following auxiliary b-graph
![]() $H_F$
. Given a Dk-graph F with b vertices and f edges, and an n-vertex Dk-graph system
$H_F$
. Given a Dk-graph F with b vertices and f edges, and an n-vertex Dk-graph system
![]() $\mathit {\mathbf {H}}=\{H_1,\dots , H_{f}\}$
on V, let
$\mathit {\mathbf {H}}=\{H_1,\dots , H_{f}\}$
on V, let
![]() $H_F$
be the (undirected) b-graph with vertex set
$H_F$
be the (undirected) b-graph with vertex set
![]() $V(H_F)=V$
and edge set
$V(H_F)=V$
and edge set
![]() $E(H_F)=\{V(F'):F'\ \mathrm {is\ a\ rainbow\ copy\ of}\ F\ \mathrm {with\ color\ set}\ [f]\}$
.
$E(H_F)=\{V(F'):F'\ \mathrm {is\ a\ rainbow\ copy\ of}\ F\ \mathrm {with\ color\ set}\ [f]\}$
.
Definition 2.4 (
 $c_{d,F}^{\mathrm {cov,*}}$
: Rainbow almost F-factor threshold).
$c_{d,F}^{\mathrm {cov,*}}$
: Rainbow almost F-factor threshold).
Let
![]() $c_{d,F}^{\mathrm {cov,*}}\in (0,1)$
be the infimum of reals
$c_{d,F}^{\mathrm {cov,*}}\in (0,1)$
be the infimum of reals
![]() $c>0$
, such that for every
$c>0$
, such that for every
![]() $\varepsilon>0$
, the following holds for sufficiently large
$\varepsilon>0$
, the following holds for sufficiently large
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
![]() $\textbf H=\{H_1,\dots , H_{f}\}$
be an n-vertex Dk-graph system. If
$\textbf H=\{H_1,\dots , H_{f}\}$
be an n-vertex Dk-graph system. If
![]() $\delta _d^*(H_i)\ge (c+\varepsilon )\binom {n-d}{k-d}$
for every
$\delta _d^*(H_i)\ge (c+\varepsilon )\binom {n-d}{k-d}$
for every
![]() $i\in [f]$
, then the b-graph
$i\in [f]$
, then the b-graph
![]() $H_F$
has a perfect fractional matching.
$H_F$
has a perfect fractional matching.
The property of “having a perfect fractional matching” is required in
![]() $H_F$
, which is a single host graph. This definition (and our proofs supporting it) establishes a close relation between the rainbow F-factor problem and the classical F-factor problem with no colors.
$H_F$
, which is a single host graph. This definition (and our proofs supporting it) establishes a close relation between the rainbow F-factor problem and the classical F-factor problem with no colors.
Now we are ready to state our general result on rainbow F-factors.
Theorem 2.5. Let F be a Dk-graph with b vertices and f edges. For any
![]() $\varepsilon>0$
and integer
$\varepsilon>0$
and integer
![]() $d\in [k-1]$
, the following holds for sufficiently large
$d\in [k-1]$
, the following holds for sufficiently large
![]() $n\in b\mathbb {N}$
. Let
$n\in b\mathbb {N}$
. Let
![]() $\textbf G=\{G_1,\dots , G_{nf/b}\}$
be an n-vertex Dk-graph system on V. If
$\textbf G=\{G_1,\dots , G_{nf/b}\}$
be an n-vertex Dk-graph system on V. If
![]() $\delta _d^*(G_i)\ge (\max \{c_{d, F}^{\mathrm {abs,*}}, c_{d, F}^{\mathrm {cov,*}}\}+\varepsilon )\binom {n-d}{k-d}$
for
$\delta _d^*(G_i)\ge (\max \{c_{d, F}^{\mathrm {abs,*}}, c_{d, F}^{\mathrm {cov,*}}\}+\varepsilon )\binom {n-d}{k-d}$
for
![]() $i\in [nf/b]$
, then
$i\in [nf/b]$
, then
![]() $\textbf G$
contains a rainbow F-factor.
$\textbf G$
contains a rainbow F-factor.
Theorem 2.5 reduces the rainbow F-factor problem to two subproblems, namely, the enumeration of rainbow F-absorbers and the study of perfect fractional matchings in
![]() $H_F$
. In our proofs of Theorems 1.3–1.7, the first subproblem is done by greedy constructions of the
$H_F$
. In our proofs of Theorems 1.3–1.7, the first subproblem is done by greedy constructions of the
![]() $K_t$
-absorbers with the minimum degree condition. Note that the second subproblem is trivial by definition for Theorem 1.7. For Theorems 1.3–1.6, we achieve it by converting the problem to the setting of complexes (downward-closed hypergraphs) and then applying a result of Keevash and Mycroft [Reference Joos and Kim23] on perfect fractional matchings, which is a nice application of the Farkas’s Lemma for linear programming. To conclude, we remark that the main benefit from Theorem 2.5 is that both of these two subproblems only concern finitely many colors. From this aspect, Theorem 2.5 irons out significant difficulties on the rainbow spanning structure problem due to an unbound number of colors. Thus, it is likely that Theorem 2.5 will find more applications in this area.
$K_t$
-absorbers with the minimum degree condition. Note that the second subproblem is trivial by definition for Theorem 1.7. For Theorems 1.3–1.6, we achieve it by converting the problem to the setting of complexes (downward-closed hypergraphs) and then applying a result of Keevash and Mycroft [Reference Joos and Kim23] on perfect fractional matchings, which is a nice application of the Farkas’s Lemma for linear programming. To conclude, we remark that the main benefit from Theorem 2.5 is that both of these two subproblems only concern finitely many colors. From this aspect, Theorem 2.5 irons out significant difficulties on the rainbow spanning structure problem due to an unbound number of colors. Thus, it is likely that Theorem 2.5 will find more applications in this area.
3 Notation and preliminary
For a hypergraph H, the 2-degree of a pair of vertices is the number of edges containing this pair and
![]() $\Delta _2(H)$
denotes the maximum 2-degree in H. For reals
$\Delta _2(H)$
denotes the maximum 2-degree in H. For reals
![]() $a, b$
, and c, we write
$a, b$
, and c, we write
![]() $a = (1\pm b)c$
for
$a = (1\pm b)c$
for
![]() $(1-b)c \leq a\leq (1+b)c$
. We need the following result which was attributed to Pippenger [Reference Lu and Yu37] (see Theorem 4.7.1 in [Reference Alon and Spencer6]), following Frankl and Rödl [Reference Rödl, Ruciński and Szemerédi43]. A cover in a hypergraph H is a set of edges, such that each vertex of H is in at least one edge of the set.
$(1-b)c \leq a\leq (1+b)c$
. We need the following result which was attributed to Pippenger [Reference Lu and Yu37] (see Theorem 4.7.1 in [Reference Alon and Spencer6]), following Frankl and Rödl [Reference Rödl, Ruciński and Szemerédi43]. A cover in a hypergraph H is a set of edges, such that each vertex of H is in at least one edge of the set.
Lemma 3.1 [Reference Lu and Yu37].
For every integer
![]() $k\geq 2$
,
$k\geq 2$
,
![]() $r\geq 1$
, and
$r\geq 1$
, and
![]() $a>0$
, there exist
$a>0$
, there exist
![]() $\gamma =\gamma (k,r,a)>0$
and
$\gamma =\gamma (k,r,a)>0$
and
![]() $d_0=d_0(d,r,a)$
, such that the following holds for every
$d_0=d_0(d,r,a)$
, such that the following holds for every
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $D\geq d_0$
. Every k-graph
$D\geq d_0$
. Every k-graph
![]() $H=(V,E)$
on V of n vertices in which all vertices have positive degrees and which satisfies the following conditions:
$H=(V,E)$
on V of n vertices in which all vertices have positive degrees and which satisfies the following conditions:
-
• For all vertices
 $x\in V$
but at most
$x\in V$
but at most
 $\gamma n$
of them,
$\gamma n$
of them,
 $d_H(x)=(1\pm \gamma )D$
.
$d_H(x)=(1\pm \gamma )D$
. -
• For all
 $x\in V$
,
$x\in V$
,
 $d_H(x)<rD$
.
$d_H(x)<rD$
. -
•
 $\Delta _2(H)<\gamma D$
.
$\Delta _2(H)<\gamma D$
.
contains a cover of at most
![]() $(1+a)(n/k)$
edges.
$(1+a)(n/k)$
edges.
The following well-known concentration results, that is Chernoff bounds, can be found in Appendix A in [Reference Alon and Spencer6] and Theorem 2.8, inequalities (2.9) and (2.11) in [Reference Huang, Li and Wang20]. Denote a binomial random variable with parameters n and p by
![]() $Bi(n,p)$
. Bernoulli’ distribution is the discrete probability distribution of a random variable which takes the value 1 with probability p and the value 0 with probability 1–p. Janson’s inequality [Reference Alon and Spencer6].
$Bi(n,p)$
. Bernoulli’ distribution is the discrete probability distribution of a random variable which takes the value 1 with probability p and the value 0 with probability 1–p. Janson’s inequality [Reference Alon and Spencer6].
Lemma 3.2 (Chernoff inequality for small deviation).
If
![]() $X=\sum _{i=1}^nX_i$
, where
$X=\sum _{i=1}^nX_i$
, where
![]() $X_1,\ldots ,X_n$
are mutually independent random variables, each
$X_1,\ldots ,X_n$
are mutually independent random variables, each
![]() $X_i$
has Bernoulli distribution with expectation
$X_i$
has Bernoulli distribution with expectation
![]() $p_i$
and
$p_i$
and
![]() $\alpha \leq 3/2$
, then
$\alpha \leq 3/2$
, then
In particular, when
![]() $X\sim Bi(n,p)$
and
$X\sim Bi(n,p)$
and
![]() $\lambda <\frac {3}{2}np$
, then
$\lambda <\frac {3}{2}np$
, then
Lemma 3.3 (Chernoff inequality for large deviation).
If
![]() $X=\sum _{i=1}^nX_i$
, where
$X=\sum _{i=1}^nX_i$
, where
![]() $X_1,\ldots ,X_n$
are mutually independent random variables, each random variable
$X_1,\ldots ,X_n$
are mutually independent random variables, each random variable
![]() $X_i$
has Bernoulli distribution with expectation
$X_i$
has Bernoulli distribution with expectation
![]() $p_i$
and
$p_i$
and
![]() $x\geq 7\mathbb {E}[X]$
, then
$x\geq 7\mathbb {E}[X]$
, then
We also need the Janson’s inequality to provide an exponential upper bound for the lower tail of a sum of dependent zero-one random variables.
Lemma 3.4 (Theorem 8.7.2 in [Reference Alon and Spencer6]).
Let
![]() $\Gamma $
be a finite set and
$\Gamma $
be a finite set and
![]() $p_i\in [0,1]$
be a real for
$p_i\in [0,1]$
be a real for
![]() $i\in \Gamma $
. Let
$i\in \Gamma $
. Let
![]() $\Gamma _p$
be a random subset of
$\Gamma _p$
be a random subset of
![]() $\Gamma $
, such that the elements are chosen independently with
$\Gamma $
, such that the elements are chosen independently with
![]() $\mathbb {P}[i\in \Gamma _p]=p_i$
for
$\mathbb {P}[i\in \Gamma _p]=p_i$
for
![]() $i\in \Gamma $
. Let M be a family of subsets of
$i\in \Gamma $
. Let M be a family of subsets of
![]() $\Gamma $
. For every
$\Gamma $
. For every
![]() $A_i\in M$
, let
$A_i\in M$
, let
![]() $I_{A_i}=1$
if
$I_{A_i}=1$
if
![]() $A_i\subseteq \Gamma _p$
and 0 otherwise. Let
$A_i\subseteq \Gamma _p$
and 0 otherwise. Let
![]() $B_i$
be the event that
$B_i$
be the event that
![]() $A_i\subseteq \Gamma _p$
. For
$A_i\subseteq \Gamma _p$
. For
![]() $A_i, A_j\in M$
, we write
$A_i, A_j\in M$
, we write
![]() $i\sim j$
if
$i\sim j$
if
![]() $B_i$
and
$B_i$
and
![]() $B_j$
are not pairwise independent, in other words,
$B_j$
are not pairwise independent, in other words,
![]() $A_i\cap A_j\neq \emptyset $
. Define
$A_i\cap A_j\neq \emptyset $
. Define
![]() $X=\Sigma _{A_i\in M}I_{A_i}$
,
$X=\Sigma _{A_i\in M}I_{A_i}$
,
![]() $\lambda =\mathbb {E}[X]$
,
$\lambda =\mathbb {E}[X]$
,
![]() $\Delta =\sum \limits _{i\sim j}\mathbb {P}[B_i\wedge B_j]$
, then
$\Delta =\sum \limits _{i\sim j}\mathbb {P}[B_i\wedge B_j]$
, then
4 Rainbow Absorption Method
4.1 Rainbow Absorption Lemma
In this section, we prove a rainbow version of the absorption lemma via probabilistic method. The only difference is that we use the following auxiliary hypergraph which makes it applicable to the rainbow setting.
Definition 4.1. We call a hypergraph H a
![]() $(1,b)$
-graph, if
$(1,b)$
-graph, if
![]() $V(H)$
can be partitioned into
$V(H)$
can be partitioned into
![]() $A\cup B$
and
$A\cup B$
and
![]() $E(H)$
is a family of
$E(H)$
is a family of
![]() $(1+b)$
-sets, each of which contains exactly one vertex in A and b vertices in B.
$(1+b)$
-sets, each of which contains exactly one vertex in A and b vertices in B.
For a
![]() $(1,b)$
-graph H with partition
$(1,b)$
-graph H with partition
![]() $A\dot \cup B$
, a
$A\dot \cup B$
, a
![]() $(1,d)$
-subset D of
$(1,d)$
-subset D of
![]() $V(H)$
is a
$V(H)$
is a
![]() $(d+1)$
-tuple, where
$(d+1)$
-tuple, where
![]() $|D\cap A|=1$
and
$|D\cap A|=1$
and
![]() $|D\cap B|=d$
. A
$|D\cap B|=d$
. A
![]() $(1,b)$
-graph H with partition classes
$(1,b)$
-graph H with partition classes
![]() $A,B$
is balanced if
$A,B$
is balanced if
![]() $b|A|=|B|$
. We say that a set
$b|A|=|B|$
. We say that a set
![]() $S\subseteq V(H)$
is balanced if
$S\subseteq V(H)$
is balanced if
![]() $b|S\cap A|=|S\cap B|$
.
$b|S\cap A|=|S\cap B|$
.
Given an n-vertex Dk-graph system
![]() $\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{nf/b}\}$
on V, we first construct a sequence of hypergraphs
$\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{nf/b}\}$
on V, we first construct a sequence of hypergraphs
![]() $H_{F_1}',\ldots ,H_{F_{n/b}}'$
, each of which is a b-graph with vertex set
$H_{F_1}',\ldots ,H_{F_{n/b}}'$
, each of which is a b-graph with vertex set
![]() $V(H_{F_i}')=V$
and edge set
$V(H_{F_i}')=V$
and edge set
![]() $E(H_{F_i}')=\{e\in \binom {V}{b}$
: e spans a rainbow copy of F with color set
$E(H_{F_i}')=\{e\in \binom {V}{b}$
: e spans a rainbow copy of F with color set
![]() $I_i=[(i-1)f+1,if]\}$
. We define an auxiliary
$I_i=[(i-1)f+1,if]\}$
. We define an auxiliary
![]() $(1,b)$
-graph
$(1,b)$
-graph
![]() $H_{\mathit {\mathbf {G}}}$
of
$H_{\mathit {\mathbf {G}}}$
of
![]() $\mathit {\mathbf {G}}$
as follows.
$\mathit {\mathbf {G}}$
as follows.
Definition 4.2. Let
![]() $H_{\textbf {G}}$
be an auxiliary
$H_{\textbf {G}}$
be an auxiliary
![]() $(1,b)$
-graph of
$(1,b)$
-graph of
![]() $\textbf {G}$
with vertex set
$\textbf {G}$
with vertex set
![]() $V'=[n/b]\cup V$
and edge set
$V'=[n/b]\cup V$
and edge set
![]() $\{\{i\}\cup e: i\in [n/b], e\in H_{F_i}'\}$
.
$\{\{i\}\cup e: i\in [n/b], e\in H_{F_i}'\}$
.
For any edge
![]() $e\in E(H_{\mathit {\mathbf {G}}})$
, if
$e\in E(H_{\mathit {\mathbf {G}}})$
, if
![]() $A\subseteq V(H_{\mathit {\mathbf {G}}})$
and
$A\subseteq V(H_{\mathit {\mathbf {G}}})$
and
![]() $|A|$
is divisible by
$|A|$
is divisible by
![]() $b+1$
, then
$b+1$
, then
![]() $A\in \binom {(b+1)n}{a}$
is an absorber for e, if
$A\in \binom {(b+1)n}{a}$
is an absorber for e, if
![]() $e\subseteq A$
, there is a perfect matching in
$e\subseteq A$
, there is a perfect matching in
![]() $H_{\mathit {\mathbf {G}}}[A]$
and there is a perfect matching in
$H_{\mathit {\mathbf {G}}}[A]$
and there is a perfect matching in
![]() $H_{\mathit {\mathbf {G}}}[A\setminus e]$
. Let
$H_{\mathit {\mathbf {G}}}[A\setminus e]$
. Let
![]() $\mathcal {L}(e)$
denote the set of absorbers for e in
$\mathcal {L}(e)$
denote the set of absorbers for e in
![]() $H_{\mathit {\mathbf {G}}}$
.
$H_{\mathit {\mathbf {G}}}$
.
Lemma 4.3 (Rainbow Absorption Lemma).
Let F be a Dk-graph with b vertices and f edges and
![]() $A^0$
be a rainbow F-absorber. The maximum vertex-disjoint copies of F of
$A^0$
be a rainbow F-absorber. The maximum vertex-disjoint copies of F of
![]() $A^0$
is m. For every
$A^0$
is m. For every
![]() $\varepsilon>0$
, there exist
$\varepsilon>0$
, there exist
![]() $\gamma ,\gamma _1$
, and
$\gamma ,\gamma _1$
, and
![]() $n_0$
, such that the following holds for all integers
$n_0$
, such that the following holds for all integers
![]() $n\geq n_0$
. Suppose that
$n\geq n_0$
. Suppose that
![]() $\textbf {G}=\{G_1,\ldots ,G_{\frac {n}{b}f}\}$
is an n-vertex Dk-graph system on V and
$\textbf {G}=\{G_1,\ldots ,G_{\frac {n}{b}f}\}$
is an n-vertex Dk-graph system on V and
![]() $\delta _d^*(G_i)\geq (c_{d,F}^{\mathrm {abs,*}}+\varepsilon )\binom {n-d}{k-d}$
and
$\delta _d^*(G_i)\geq (c_{d,F}^{\mathrm {abs,*}}+\varepsilon )\binom {n-d}{k-d}$
and
![]() $H_{\textbf {G}}$
is the auxiliary
$H_{\textbf {G}}$
is the auxiliary
![]() $(1,b)$
-graph of
$(1,b)$
-graph of
![]() $\textbf {G}$
, then there exists a matching M in
$\textbf {G}$
, then there exists a matching M in
![]() $H_{\textbf {G}}$
with size at most
$H_{\textbf {G}}$
with size at most
![]() $2\gamma (m-1)n$
, such that for every balanced set
$2\gamma (m-1)n$
, such that for every balanced set
![]() $U\subseteq \left ([n/b]\cup V\right )\setminus V(M)$
of size at most
$U\subseteq \left ([n/b]\cup V\right )\setminus V(M)$
of size at most
![]() $\gamma _1n$
,
$\gamma _1n$
,
![]() $V(M)\cup U$
spans a matching in
$V(M)\cup U$
spans a matching in
![]() $H_{\textbf {G}}$
.
$H_{\textbf {G}}$
.
Proof. Let
![]() $1/n\ll \gamma _1\ll \alpha \ll \gamma \ll \varepsilon '\ll \varepsilon $
. Note that a matching of size m in
$1/n\ll \gamma _1\ll \alpha \ll \gamma \ll \varepsilon '\ll \varepsilon $
. Note that a matching of size m in
![]() $H_{\mathit {\mathbf {G}}}$
corresponds to a rainbow F-absorber in
$H_{\mathit {\mathbf {G}}}$
corresponds to a rainbow F-absorber in
![]() $\boldsymbol{G}$
. Choose a family
$\boldsymbol{G}$
. Choose a family
![]() $\mathcal {F}$
of matchings of size
$\mathcal {F}$
of matchings of size
![]() $m-1$
from
$m-1$
from
![]() $H_{\mathit {\mathbf {G}}}$
by including each matching of size
$H_{\mathit {\mathbf {G}}}$
by including each matching of size
![]() $m-1$
independently at random with probability
$m-1$
independently at random with probability
Note that
![]() $|\mathcal {F}|, |\mathcal {L}(e)\cap \mathcal {F}|$
are binomial random variables with expectations
$|\mathcal {F}|, |\mathcal {L}(e)\cap \mathcal {F}|$
are binomial random variables with expectations
The latter inequality holds since for any edge e of
![]() $H_{\mathit {\mathbf {G}}}$
,
$H_{\mathit {\mathbf {G}}}$
,
![]() $|\mathcal {L}(e)|\geq \varepsilon 'n^{(m-1)(b+1)}$
by the minimum degree assumption and Definition 2.3. By Lemma 3.2, with probability
$|\mathcal {L}(e)|\geq \varepsilon 'n^{(m-1)(b+1)}$
by the minimum degree assumption and Definition 2.3. By Lemma 3.2, with probability
![]() $1-o(1)$
, the family
$1-o(1)$
, the family
![]() $\mathcal {F}$
satisfies the following properties.
$\mathcal {F}$
satisfies the following properties.
-
(1)
 $|\mathcal {F}|\leq 2\mathbb {E}|\mathcal {F}|\leq 2\gamma n$
,
$|\mathcal {F}|\leq 2\mathbb {E}|\mathcal {F}|\leq 2\gamma n$
, -
(2)
 $|\mathcal {L}(e)\cap \mathcal {F}|\geq \frac {1}{2}\mathbb {E}|\mathcal {L}(e)\cap \mathcal {F}|\geq \frac {1}{2}\gamma \varepsilon 'n$
for any
$|\mathcal {L}(e)\cap \mathcal {F}|\geq \frac {1}{2}\mathbb {E}|\mathcal {L}(e)\cap \mathcal {F}|\geq \frac {1}{2}\gamma \varepsilon 'n$
for any
 $e\in E(H_{\mathit {\mathbf {G}}})$
.
$e\in E(H_{\mathit {\mathbf {G}}})$
.
Moreover, we can also bound the expected number of pairs of intersecting members of
![]() $\mathcal {F}$
by
$\mathcal {F}$
by
Thus, by Markov’s Inequality [Reference Alon and Spencer6], we derive that with probability at least
![]() $1/2$
,
$1/2$
,
![]() $\mathcal {F}$
contains at most
$\mathcal {F}$
contains at most
![]() $\frac {1}{4}\gamma \varepsilon 'n$
pairs of intersecting members of
$\frac {1}{4}\gamma \varepsilon 'n$
pairs of intersecting members of
![]() $\mathcal {F}$
. Remove one member from each of the intersecting pairs in
$\mathcal {F}$
. Remove one member from each of the intersecting pairs in
![]() $\mathcal {F}$
. Thus, the resulting family, say
$\mathcal {F}$
. Thus, the resulting family, say
![]() $\mathcal {F}'$
, consists of pairwise disjoint matchings of size
$\mathcal {F}'$
, consists of pairwise disjoint matchings of size
![]() $m-1$
that satisfies
$m-1$
that satisfies
-
(1)
 $|\mathcal {F}'|\leq 2\gamma n$
,
$|\mathcal {F}'|\leq 2\gamma n$
, -
(2)
 $|\mathcal {L}(e)\cap \mathcal {F}|\geq \frac {1}{2}\gamma \varepsilon 'n- \frac {1}{4}\gamma \varepsilon 'n\geq \alpha n$
for any
$|\mathcal {L}(e)\cap \mathcal {F}|\geq \frac {1}{2}\gamma \varepsilon 'n- \frac {1}{4}\gamma \varepsilon 'n\geq \alpha n$
for any
 $e\in E(H_{\mathit {\mathbf {G}}})$
.
$e\in E(H_{\mathit {\mathbf {G}}})$
.
Therefore, the union of members in
![]() $\mathcal {F}'$
is a matching in
$\mathcal {F}'$
is a matching in
![]() $H_{\mathit {\mathbf {G}}}$
of size at most
$H_{\mathit {\mathbf {G}}}$
of size at most
![]() $2\gamma (m-1)n$
and can (greedily) absorb a balanced set U of size at most
$2\gamma (m-1)n$
and can (greedily) absorb a balanced set U of size at most
![]() $\gamma _1n$
since
$\gamma _1n$
since
![]() $\gamma _1\ll \alpha $
.
$\gamma _1\ll \alpha $
.
4.2 Enumeration of rainbow absorbers
In this section, we give two examples of rainbow absorbers. The first one is as follows. Recall that
![]() $T_k$
is the transitive tournament on k vertices.
$T_k$
is the transitive tournament on k vertices.
4.2.1 Rainbow
 $T_k$
-absorber
$T_k$
-absorber
For the proof of Theorem 1.4, we show that
For any k-set
![]() $S=\{u_1,u_2,\ldots ,u_k\}$
in V and every
$S=\{u_1,u_2,\ldots ,u_k\}$
in V and every
![]() $\binom {k}{2}$
-set
$\binom {k}{2}$
-set
![]() $C=[(j-1)\binom {k}{2}+1,j\binom {k}{2}]$
, where
$C=[(j-1)\binom {k}{2}+1,j\binom {k}{2}]$
, where
![]() $j\in [\frac {n}{k}]$
, we define a rainbow
$j\in [\frac {n}{k}]$
, we define a rainbow
![]() $T_k$
-absorber A for
$T_k$
-absorber A for
![]() $(S,C)$
as follows (see Figure 2).
$(S,C)$
as follows (see Figure 2).
-
•
 $A_1=A-S=\{T_k^1,\ldots ,T_k^k\}$
is a rainbow
$A_1=A-S=\{T_k^1,\ldots ,T_k^k\}$
is a rainbow
 $T_k$
-tiling with
$T_k$
-tiling with
 $C(T_k^i)=[(j_i-1)\binom {k}{2}+1,j_i\binom {k}{2}]$
, where
$C(T_k^i)=[(j_i-1)\binom {k}{2}+1,j_i\binom {k}{2}]$
, where
 $j_i\in [n/k]$
for
$j_i\in [n/k]$
for
 $i\in [k]$
and
$i\in [k]$
and
 $A_2=\{T_k^{0},T_k^{1'},\ldots ,T_k^{k'}\}$
is a rainbow
$A_2=\{T_k^{0},T_k^{1'},\ldots ,T_k^{k'}\}$
is a rainbow
 $T_k$
-tiling with
$T_k$
-tiling with
 $C(T_k^{0})=C$
and
$C(T_k^{0})=C$
and
 $C(T_k^{i'})=[(j_i-1)\binom {k}{2}+1,j_i\binom {k}{2}]$
, where
$C(T_k^{i'})=[(j_i-1)\binom {k}{2}+1,j_i\binom {k}{2}]$
, where
 $j_i\in [n/k]$
for
$j_i\in [n/k]$
for
 $i\in [k]$
.
$i\in [k]$
. -
• We can choose a rainbow
 $T_k^{0}$
that is isomorphic to
$T_k^{0}$
that is isomorphic to
 $T_k$
with color set C, such that
$T_k$
with color set C, such that
 $V(T_k^{0})=\{v_1,v_2,\ldots ,v_k\}$
, where
$V(T_k^{0})=\{v_1,v_2,\ldots ,v_k\}$
, where
 $v_i\in V(T_k^i)$
and
$v_i\in V(T_k^i)$
and
 $V(T_k^{i'})=V(T_k^i)\backslash \{v_i\}\cup \{u_i\}, i\in [k]$
.
$V(T_k^{i'})=V(T_k^i)\backslash \{v_i\}\cup \{u_i\}, i\in [k]$
. -
•
 $c(u_ix)=c(v_ix)$
for each
$c(u_ix)=c(v_ix)$
for each
 $x\in V(A_1\backslash V(T_k^{0}))$
, and
$x\in V(A_1\backslash V(T_k^{0}))$
, and
 $c(xy)$
in
$c(xy)$
in
 $T_k^i$
is the same as
$T_k^i$
is the same as
 $c(xy)$
in
$c(xy)$
in
 $T_k^{i'}$
for
$T_k^{i'}$
for
 $i\in [k]$
and
$i\in [k]$
and
 $x,y\in V(A_1\backslash V(T_k^{0}))$
.
$x,y\in V(A_1\backslash V(T_k^{0}))$
.

Figure 2 Illustration of the rainbow absorbers (with directions omitted).
Suppose
![]() $\delta (D_i^+)\ge (1-1/k+\varepsilon )n$
for
$\delta (D_i^+)\ge (1-1/k+\varepsilon )n$
for
![]() $i\in [\frac {n}{k}\binom {k}{2}]$
. For any k-set S in V and every
$i\in [\frac {n}{k}\binom {k}{2}]$
. For any k-set S in V and every
![]() $\binom {k}{2}$
-set
$\binom {k}{2}$
-set
![]() $C=[(j-1)\binom {k}{2}+1,j\binom {k}{2}]$
, where
$C=[(j-1)\binom {k}{2}+1,j\binom {k}{2}]$
, where
![]() $j\in [\frac {n}{k}]$
, we denote the family of rainbow
$j\in [\frac {n}{k}]$
, we denote the family of rainbow
![]() $T_k$
-absorbers for
$T_k$
-absorbers for
![]() $(S,C)$
by
$(S,C)$
by
![]() $\mathcal {A}(S,C)$
.
$\mathcal {A}(S,C)$
.
Claim 4.4. For any k-set
![]() $S=\{u_1,u_2,\ldots ,u_k\}$
in V and every
$S=\{u_1,u_2,\ldots ,u_k\}$
in V and every
![]() $\binom {k}{2}$
-set
$\binom {k}{2}$
-set
![]() $C=[(j-1)\binom {k}{2}+1,j\binom {k}{2}]$
where
$C=[(j-1)\binom {k}{2}+1,j\binom {k}{2}]$
where
![]() $j\in [\frac {n}{k}]$
, we have
$j\in [\frac {n}{k}]$
, we have
![]() $|\mathcal {A}(S,C)|\geq \varepsilon ^{k^2+k}n^{k^2+k}$
.
$|\mathcal {A}(S,C)|\geq \varepsilon ^{k^2+k}n^{k^2+k}$
.
Proof. Fixing a k-set
![]() $S=\{u_1,u_2,\ldots ,u_k\}$
in V and a
$S=\{u_1,u_2,\ldots ,u_k\}$
in V and a
![]() $\binom {k}{2}$
-set
$\binom {k}{2}$
-set
![]() $C=[(j-1)\binom {k}{2}+1,j\binom {k}{2}]$
for some
$C=[(j-1)\binom {k}{2}+1,j\binom {k}{2}]$
for some
![]() $j\in [\frac {n}{k}]$
, we construct rainbow absorbers for
$j\in [\frac {n}{k}]$
, we construct rainbow absorbers for
![]() $(S,C)$
. We choose
$(S,C)$
. We choose
![]() $[(j_{i}-1)\binom {k}{2}+1,j_i\binom {k}{2}]$
for
$[(j_{i}-1)\binom {k}{2}+1,j_i\binom {k}{2}]$
for
![]() $i\in [k]$
arbitrarily, there are
$i\in [k]$
arbitrarily, there are
![]() $(\frac {n}{k}-1)(\frac {n}{k}-2)\cdots (\frac {n}{k}-k)\geq \varepsilon ^kn^k$
choices. Next, we choose a rainbow
$(\frac {n}{k}-1)(\frac {n}{k}-2)\cdots (\frac {n}{k}-k)\geq \varepsilon ^kn^k$
choices. Next, we choose a rainbow
![]() $T_k^0$
with color set C. Due to the minimum out-degree of
$T_k^0$
with color set C. Due to the minimum out-degree of
![]() $D_i$
, the number of choices for
$D_i$
, the number of choices for
![]() $T_k^0$
is at least
$T_k^0$
is at least
 $$\begin{align*}(n-k)\left((1-\frac{1}{k}+\varepsilon)n-(k+1)\right) \cdots \left(\frac{1}{k}+(k-1)\varepsilon n-(2k-1)\right)\geq \varepsilon^kn^k. \end{align*}$$
$$\begin{align*}(n-k)\left((1-\frac{1}{k}+\varepsilon)n-(k+1)\right) \cdots \left(\frac{1}{k}+(k-1)\varepsilon n-(2k-1)\right)\geq \varepsilon^kn^k. \end{align*}$$
Now we fix one such
![]() $U=\{v_1,v_2,\ldots ,v_k\}$
. For each
$U=\{v_1,v_2,\ldots ,v_k\}$
. For each
![]() $i\in [k]$
and each pair
$i\in [k]$
and each pair
![]() $\{u_i,v_i\}$
, suppose we succeed in choosing a set
$\{u_i,v_i\}$
, suppose we succeed in choosing a set
![]() $S_i$
, such that
$S_i$
, such that
![]() $S_i$
is disjoint to
$S_i$
is disjoint to
![]() $W_{i-1} = \cup _{j\in [i-1]}S_j\cup S\cup U$
, then
$W_{i-1} = \cup _{j\in [i-1]}S_j\cup S\cup U$
, then
![]() $V(T_k^{i'})=S_i\cup \{u_i\}$
spans a rainbow
$V(T_k^{i'})=S_i\cup \{u_i\}$
spans a rainbow
![]() $T_k$
in
$T_k$
in
![]() $\mathit {\mathbf {D}}$
with color set
$\mathit {\mathbf {D}}$
with color set
![]() $[(j_i-1)\binom {k}{2}+1,j_i\binom {k}{2}]$
while so does
$[(j_i-1)\binom {k}{2}+1,j_i\binom {k}{2}]$
while so does
![]() $V(T_k^i)=S_i\cup \{v_i\}$
.
$V(T_k^i)=S_i\cup \{v_i\}$
.
For the first vertex in
![]() $S_1$
, the number of choices is at least
$S_1$
, the number of choices is at least
![]() $(1-\frac {2}{k}+2\varepsilon )n-2k$
, for the last vertex in
$(1-\frac {2}{k}+2\varepsilon )n-2k$
, for the last vertex in
![]() $S_1$
, the number of choices is in
$S_1$
, the number of choices is in
![]() $k\varepsilon n-(3k-1)$
. Since
$k\varepsilon n-(3k-1)$
. Since
![]() $\frac {1}{n}\ll \varepsilon $
, the number of choices for
$\frac {1}{n}\ll \varepsilon $
, the number of choices for
![]() $S_1$
is at least
$S_1$
is at least
 $$\begin{align*}\left((1-\frac{2}{k}+2\varepsilon)n-2k\right) \cdots (k\varepsilon n-(3k-1))\geq\varepsilon^{k-1}n^{k-1}. \end{align*}$$
$$\begin{align*}\left((1-\frac{2}{k}+2\varepsilon)n-2k\right) \cdots (k\varepsilon n-(3k-1))\geq\varepsilon^{k-1}n^{k-1}. \end{align*}$$
Similarly, the minimum out-degree implies that for
![]() $i\in [2,k]$
, there are at least
$i\in [2,k]$
, there are at least
![]() $\varepsilon ^{k-1}n^{k-1}$
choices for
$\varepsilon ^{k-1}n^{k-1}$
choices for
![]() $S_i$
and, in total, we obtain
$S_i$
and, in total, we obtain
![]() $\varepsilon ^{k^2+k}n^{k^2+k}$
rainbow
$\varepsilon ^{k^2+k}n^{k^2+k}$
rainbow
![]() $T_k$
-absorbers for S.
$T_k$
-absorbers for S.
4.2.2 Rainbow edge-absorber
For the proof of Theorem 1.7, we show that
Given an n-vertex k-graph system
![]() $\mathit {\mathbf {G}}$
on V with
$\mathit {\mathbf {G}}$
on V with
![]() $\delta _d(G_i)\geq (\frac {1}{2}+\varepsilon )\binom {n-d}{k-d}$
for
$\delta _d(G_i)\geq (\frac {1}{2}+\varepsilon )\binom {n-d}{k-d}$
for
![]() $i\in [n/k]$
, we first construct a
$i\in [n/k]$
, we first construct a
![]() $(1,k)$
-graph
$(1,k)$
-graph
![]() $H_{\mathit {\mathbf {G}}}$
with vertex set
$H_{\mathit {\mathbf {G}}}$
with vertex set
![]() $[n/k]\cup V$
and edge set
$[n/k]\cup V$
and edge set
![]() $\{\{i\}\cup e:e\in H_i,i\in [n/k]\}$
. Next, we construct a specific rainbow edge-absorber. For any k-set
$\{\{i\}\cup e:e\in H_i,i\in [n/k]\}$
. Next, we construct a specific rainbow edge-absorber. For any k-set
![]() $T=\{v_1,\ldots ,v_k\}$
in V and every color
$T=\{v_1,\ldots ,v_k\}$
in V and every color
![]() $c_1\in [n/k]$
, we give a rainbow absorber
$c_1\in [n/k]$
, we give a rainbow absorber
![]() $A=A_1\cup A_2$
for
$A=A_1\cup A_2$
for
![]() $(T,c_1)$
as follows.
$(T,c_1)$
as follows.
-
•
 $A_1=\{M_2,\ldots ,M_k\}$
is a set of
$A_1=\{M_2,\ldots ,M_k\}$
is a set of
 $k-1$
disjoint edges in
$k-1$
disjoint edges in
 $H_{\mathit {\mathbf {G}}}$
, where
$H_{\mathit {\mathbf {G}}}$
, where
 $c_i\in M_i(i\in [2,k])$
.
$c_i\in M_i(i\in [2,k])$
. -
• There is a vertex
 $u_i(i\in [2,k])$
from each
$u_i(i\in [2,k])$
from each
 $V(M_i)$
, such that
$V(M_i)$
, such that
 $\{u_2,\ldots ,u_k, v_1, c_1\}\in E(H_{\mathit {\mathbf {G}}})$
and
$\{u_2,\ldots ,u_k, v_1, c_1\}\in E(H_{\mathit {\mathbf {G}}})$
and
 $(V(M_i)\setminus \{u_i\})\cup \{v_i\}\in E(H_{\mathit {\mathbf {G}}})$
for
$(V(M_i)\setminus \{u_i\})\cup \{v_i\}\in E(H_{\mathit {\mathbf {G}}})$
for
 $i\in [2,k]$
. Let
$i\in [2,k]$
. Let
 $A_2$
be
$A_2$
be
 $\{\{u_2,\ldots ,u_k, v_1, c_1\},(V(M_2)\setminus \{u_2\})\cup \{v_2\},\ldots ,(V(M_k)\setminus \{u_k\})\cup \{v_k\}\}$
.
$\{\{u_2,\ldots ,u_k, v_1, c_1\},(V(M_2)\setminus \{u_2\})\cup \{v_2\},\ldots ,(V(M_k)\setminus \{u_k\})\cup \{v_k\}\}$
.
For any k-set T in V and every color
![]() $c_1\in [n/k]$
, we denote the family of such rainbow edge-absorbers for
$c_1\in [n/k]$
, we denote the family of such rainbow edge-absorbers for
![]() $(T,c_1)$
by
$(T,c_1)$
by
![]() $\mathcal {A}(T,c_1)$
.
$\mathcal {A}(T,c_1)$
.
Claim 4.5.
![]() $|\mathcal {A}(T,c_1)|\geq \varepsilon ^{2k-2}n^{k-1} \binom {n-1}{k-1}^k/2$
.
$|\mathcal {A}(T,c_1)|\geq \varepsilon ^{2k-2}n^{k-1} \binom {n-1}{k-1}^k/2$
.
Proof. Fix
![]() $c_1\in [n/k]$
and
$c_1\in [n/k]$
and
![]() $T=\{v_1,\ldots ,v_k\}\subseteq V$
. Choose
$T=\{v_1,\ldots ,v_k\}\subseteq V$
. Choose
![]() $(c_2,\ldots ,c_k)$
arbitrarily from
$(c_2,\ldots ,c_k)$
arbitrarily from
![]() $[n/k]$
, and there are at least
$[n/k]$
, and there are at least
![]() $(\frac {n}{k}-1)\cdots (\frac {n}{k}-(k-1))\geq \varepsilon ^{k-1}n^{k-1}$
choices. Fix such
$(\frac {n}{k}-1)\cdots (\frac {n}{k}-(k-1))\geq \varepsilon ^{k-1}n^{k-1}$
choices. Fix such
![]() $(c_2,\ldots ,c_k)$
. Next, we construct
$(c_2,\ldots ,c_k)$
. Next, we construct
![]() $M_2,\ldots ,M_k$
, and note that there are at most
$M_2,\ldots ,M_k$
, and note that there are at most
![]() $(k-1)\binom {n-1}{k-2}\leq \varepsilon \binom {n-1}{k-1}$
edges which contain
$(k-1)\binom {n-1}{k-2}\leq \varepsilon \binom {n-1}{k-1}$
edges which contain
![]() $c_1, v_1$
, and
$c_1, v_1$
, and
![]() $v_j$
for some
$v_j$
for some
![]() $j\in [2,k]$
. Due to the minimum degree assumption, there are at least
$j\in [2,k]$
. Due to the minimum degree assumption, there are at least
![]() $\frac {1}{2}\binom {n-1}{k-1}$
edges containing
$\frac {1}{2}\binom {n-1}{k-1}$
edges containing
![]() $v_1$
and
$v_1$
and
![]() $c_1$
but none of
$c_1$
but none of
![]() $v_2,\ldots ,v_k$
. We fix such one edge
$v_2,\ldots ,v_k$
. We fix such one edge
![]() $\{c_1,v_1,u_2,\ldots ,u_k\}$
and set
$\{c_1,v_1,u_2,\ldots ,u_k\}$
and set
![]() $U_1=\{u_2,\ldots ,u_k\}$
. For each
$U_1=\{u_2,\ldots ,u_k\}$
. For each
![]() $i\in [2,k]$
and each pair
$i\in [2,k]$
and each pair
![]() $\{u_i,v_i\}$
, suppose we succeed in choosing a set
$\{u_i,v_i\}$
, suppose we succeed in choosing a set
![]() $U_i$
, such that
$U_i$
, such that
![]() $U_i$
is disjoint with
$U_i$
is disjoint with
![]() $W_{i-1}=\cup _{j\in [i-1]}U_j\cup T$
and both
$W_{i-1}=\cup _{j\in [i-1]}U_j\cup T$
and both
![]() $U_i\cup \{u_i,c_i\}$
and
$U_i\cup \{u_i,c_i\}$
and
![]() $U_i\cup \{v_i, c_i\}$
are edges in
$U_i\cup \{v_i, c_i\}$
are edges in
![]() $\tilde {H}$
, then for a fixed
$\tilde {H}$
, then for a fixed
![]() $i\in [2,k]$
, we call such a choice
$i\in [2,k]$
, we call such a choice
![]() $U_i$
good.
$U_i$
good.
Note that in each step
![]() $i\in [2,k]$
, there are
$i\in [2,k]$
, there are
![]() $k+(i-1)(k-1)\leq k^2$
vertices in
$k+(i-1)(k-1)\leq k^2$
vertices in
![]() $W_{i-1}$
, thus the number of edges with color
$W_{i-1}$
, thus the number of edges with color
![]() $c_i$
intersecting
$c_i$
intersecting
![]() $u_i$
and at least one other vertex in
$u_i$
and at least one other vertex in
![]() $W_{i-1}$
is at most
$W_{i-1}$
is at most
![]() $k^2\binom {n-1}{k-2}$
. So the minimum degree assumption implies that for each
$k^2\binom {n-1}{k-2}$
. So the minimum degree assumption implies that for each
![]() $i\in [2,k]$
, there are at least
$i\in [2,k]$
, there are at least
![]() $2\varepsilon \binom {n-1}{k-1}-2k^2\binom {n-1}{k-2}\geq \varepsilon \binom {n-1}{k-1}$
choices for
$2\varepsilon \binom {n-1}{k-1}-2k^2\binom {n-1}{k-2}\geq \varepsilon \binom {n-1}{k-1}$
choices for
![]() $U_i$
, and, in total, we obtain
$U_i$
, and, in total, we obtain
![]() $\varepsilon ^{2k-2}n^{k-1} \binom {n-1}{k-1}^k/2$
rainbow absorbers for
$\varepsilon ^{2k-2}n^{k-1} \binom {n-1}{k-1}^k/2$
rainbow absorbers for
![]() $(T,c_1)$
.
$(T,c_1)$
.
5 Rainbow almost cover
The goal of this section is to prove the following lemma, an important component of the proof of Theorem 2.5.
Lemma 5.1 (Rainbow almost cover lemma).
Let F be a Dk-graph with b vertices and f edges. For every
![]() $\varepsilon , \phi>0$
and integer
$\varepsilon , \phi>0$
and integer
![]() $d\in [k-1]$
, the following holds for sufficiently large
$d\in [k-1]$
, the following holds for sufficiently large
![]() $n\in b\mathbb {N}$
. Suppose that
$n\in b\mathbb {N}$
. Suppose that
![]() $\textbf {G}=\{G_1,\ldots ,G_{nf/b}\}$
is an n-vertex Dk-graph system on V, such that
$\textbf {G}=\{G_1,\ldots ,G_{nf/b}\}$
is an n-vertex Dk-graph system on V, such that
![]() $\delta _d^*(G_i)\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon )\binom {n-d}{k-d}$
for
$\delta _d^*(G_i)\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon )\binom {n-d}{k-d}$
for
![]() $i\in [nf/b]$
, then
$i\in [nf/b]$
, then
![]() $\textbf {G}$
contains a rainbow F-tiling covering all but at most
$\textbf {G}$
contains a rainbow F-tiling covering all but at most
![]() $\phi n$
vertices.
$\phi n$
vertices.
For a k-graph H, a fractional cover is a function
![]() $\omega :V(H)\to [0,1]$
, subject to the requirement
$\omega :V(H)\to [0,1]$
, subject to the requirement
![]() $\sum _{v:v\in e}\omega (v)\geq 1$
for every
$\sum _{v:v\in e}\omega (v)\geq 1$
for every
![]() $e\in E(H)$
. Denote the minimum fractional cover size by
$e\in E(H)$
. Denote the minimum fractional cover size by
![]() $\tau ^*(H)=\min _\omega \Sigma _{v\in V(H)}\omega (v)$
. The conclusion
$\tau ^*(H)=\min _\omega \Sigma _{v\in V(H)}\omega (v)$
. The conclusion
![]() $\nu ^*(H)=\tau ^*(H)$
for any hypergraph follows from the linear programming (LP)-duality. For n-vertex k-graphs, we trivially have
$\nu ^*(H)=\tau ^*(H)$
for any hypergraph follows from the linear programming (LP)-duality. For n-vertex k-graphs, we trivially have
![]() $\nu ^*(H)=\tau ^*(H)\le \frac {n}{k}$
.
$\nu ^*(H)=\tau ^*(H)\le \frac {n}{k}$
.
We construct another
![]() $(1,b)$
-graph
$(1,b)$
-graph
![]() $\tilde {H}$
on
$\tilde {H}$
on
![]() $[\frac {nf}{b}]\cup V$
with edge set
$[\frac {nf}{b}]\cup V$
with edge set
![]() $E(\tilde {H})=\{\{i\}\cup e:e\in H_i$
for all
$E(\tilde {H})=\{\{i\}\cup e:e\in H_i$
for all
![]() $i\in [nf/b]\}$
. A
$i\in [nf/b]\}$
. A
![]() $(1,k-1)$
-subset S of
$(1,k-1)$
-subset S of
![]() $V(\tilde {H})$
contains one vertex in
$V(\tilde {H})$
contains one vertex in
![]() $[\frac {nf}{b}]$
and
$[\frac {nf}{b}]$
and
![]() $k-1$
vertices in V. Let
$k-1$
vertices in V. Let
![]() $\delta _{1,k-1}(\tilde {H}):=\min \{\deg _{\tilde {H}}(S):\ S \text { is a } (1,k-1)\text {-subset of } V(\tilde {H})\}$
, where
$\delta _{1,k-1}(\tilde {H}):=\min \{\deg _{\tilde {H}}(S):\ S \text { is a } (1,k-1)\text {-subset of } V(\tilde {H})\}$
, where
![]() $\deg _{\tilde {H}}(S)$
denotes the number of edges in
$\deg _{\tilde {H}}(S)$
denotes the number of edges in
![]() $\tilde {H}$
containing S. The proof of the following claim is by now a standard argument on fractional matchings and covers.
$\tilde {H}$
containing S. The proof of the following claim is by now a standard argument on fractional matchings and covers.
Claim 5.2. If each
![]() $H_{F_i}'$
contains a perfect fractional matching for
$H_{F_i}'$
contains a perfect fractional matching for
![]() $i\in [\frac {n}{b}]$
, then the auxiliary
$i\in [\frac {n}{b}]$
, then the auxiliary
![]() $(1,b)$
-graph
$(1,b)$
-graph
![]() $H_{\textbf {G}}$
of
$H_{\textbf {G}}$
of
![]() $\textbf {G}$
contains a perfect fractional matching.
$\textbf {G}$
contains a perfect fractional matching.
Proof. By the duality theorem, we transform the maximum fractional matching problem into the minimum fractional cover problem. Since
![]() $\tau ^*(H_{\mathit {\mathbf {G}}})=\nu ^*(H_{\mathit {\mathbf {G}}})\leq \frac {n}{b}$
, it suffices to show that
$\tau ^*(H_{\mathit {\mathbf {G}}})=\nu ^*(H_{\mathit {\mathbf {G}}})\leq \frac {n}{b}$
, it suffices to show that
![]() $\tau ^*(H_{\mathit {\mathbf {G}}})\geq \frac {n}{b}$
to obtain
$\tau ^*(H_{\mathit {\mathbf {G}}})\geq \frac {n}{b}$
to obtain
![]() $\nu ^*(H_{\mathit {\mathbf {G}}})=\frac {n}{b}$
. Let
$\nu ^*(H_{\mathit {\mathbf {G}}})=\frac {n}{b}$
. Let
![]() $\omega $
be the minimum fractional cover of
$\omega $
be the minimum fractional cover of
![]() $H_{\mathit {\mathbf {G}}}$
, and take
$H_{\mathit {\mathbf {G}}}$
, and take
![]() $i_1 \in [n/b]$
, such that
$i_1 \in [n/b]$
, such that
![]() $\omega (i_1):=\min _{i\in [n/b]}\omega (i)$
. We may assume that
$\omega (i_1):=\min _{i\in [n/b]}\omega (i)$
. We may assume that
![]() $\omega (i_1)=1-x<1$
, since otherwise,
$\omega (i_1)=1-x<1$
, since otherwise,
![]() $\omega ([n/b])\geq \frac {n}{b}$
, and we are done. By definition, we get
$\omega ([n/b])\geq \frac {n}{b}$
, and we are done. By definition, we get
![]() $\omega (e)\geq 1-\omega (i_1)= x$
for every
$\omega (e)\geq 1-\omega (i_1)= x$
for every
![]() $e\in H^{\prime }_{F_{i_1}}$
. We define a new weight function
$e\in H^{\prime }_{F_{i_1}}$
. We define a new weight function
![]() $\omega '$
on V by setting
$\omega '$
on V by setting
![]() $\omega '(v)=\frac {\omega (v)}{x}$
for every vertex
$\omega '(v)=\frac {\omega (v)}{x}$
for every vertex
![]() $v\in V$
. Thus,
$v\in V$
. Thus,
![]() $\omega '$
is a fractional cover of
$\omega '$
is a fractional cover of
![]() $H_{F_{i_1}}'$
because for each
$H_{F_{i_1}}'$
because for each
![]() $e\in H^{\prime }_{F_{i_1}}$
,
$e\in H^{\prime }_{F_{i_1}}$
,
![]() $\omega '(e)=\frac {\omega (e)}{x}\geq 1$
. Recall that
$\omega '(e)=\frac {\omega (e)}{x}\geq 1$
. Recall that
![]() $H^{\prime }_{F_{i_1}}$
has a perfect fractional matching, and thus,
$H^{\prime }_{F_{i_1}}$
has a perfect fractional matching, and thus,
![]() $\omega '(V)\geq \tau ^*(H_{F_{i_1}}')\geq \frac {n}{b}$
which implies that
$\omega '(V)\geq \tau ^*(H_{F_{i_1}}')\geq \frac {n}{b}$
which implies that
![]() $\omega (V)\geq \frac {xn}{b}$
. Therefore,
$\omega (V)\geq \frac {xn}{b}$
. Therefore,
Hence,
![]() $\tau ^*(H_{\mathit {\mathbf {G}}})=\frac {n}{b}$
, that is
$\tau ^*(H_{\mathit {\mathbf {G}}})=\frac {n}{b}$
, that is
![]() $H_{\mathit {\mathbf {G}}}$
contains a perfect fractional matching.
$H_{\mathit {\mathbf {G}}}$
contains a perfect fractional matching.
In this section, given an n-vertex Dk-graph system
![]() $\mathit {\mathbf {G}}$
, we shall construct an auxiliary
$\mathit {\mathbf {G}}$
, we shall construct an auxiliary
![]() $(1,b)$
-graph
$(1,b)$
-graph
![]() $H_{\mathit {\mathbf {G}}}$
of
$H_{\mathit {\mathbf {G}}}$
of
![]() $\mathit {\mathbf {G}}$
and a sequence of random subgraphs of
$\mathit {\mathbf {G}}$
and a sequence of random subgraphs of
![]() $H_{\mathit {\mathbf {G}}}$
. Then, we use the properties of them to get a “near regular” spanning subgraph for the sake of applying Lemma 3.1.
$H_{\mathit {\mathbf {G}}}$
. Then, we use the properties of them to get a “near regular” spanning subgraph for the sake of applying Lemma 3.1.
The proof is based on a two-round randomization, which is already used in [Reference Alon, Frankl, Huang, Rödl, Ruciński and Sudakov5, Reference Lo and Markström34, Reference Lu, Wang and Yu36]. Since we work with balanced
![]() $(1,b)$
-graphs, we need to make sure that each random graph is balanced. In order to achieve this, we modify the randomization process by fixing an arbitrarily small and balanced set
$(1,b)$
-graphs, we need to make sure that each random graph is balanced. In order to achieve this, we modify the randomization process by fixing an arbitrarily small and balanced set
![]() $S\subseteq V(H_{\mathit {\mathbf {G}}})$
. This is done in Fact 1.
$S\subseteq V(H_{\mathit {\mathbf {G}}})$
. This is done in Fact 1.
Let
![]() $H_{\mathit {\mathbf {G}}}$
be the auxiliary
$H_{\mathit {\mathbf {G}}}$
be the auxiliary
![]() $(1,b)$
-graph of
$(1,b)$
-graph of
![]() $\mathit {\mathbf {G}}$
with partition classes A, B, and
$\mathit {\mathbf {G}}$
with partition classes A, B, and
![]() $b|A|=|B|$
, where A is the color set and
$b|A|=|B|$
, where A is the color set and
![]() $B=V$
. Let
$B=V$
. Let
![]() $S\subseteq V(H_{\mathit {\mathbf {G}}})$
be a set of vertices, such that
$S\subseteq V(H_{\mathit {\mathbf {G}}})$
be a set of vertices, such that
![]() $|S\cap A|=n^{0.99}/b$
and
$|S\cap A|=n^{0.99}/b$
and
![]() $|S\cap B|=n^{0.99}$
. The desired subgraph
$|S\cap B|=n^{0.99}$
. The desired subgraph
![]() $H"$
is obtained by two rounds of randomization. As a preparation to the first round, we choose every vertex randomly and uniformly with probability
$H"$
is obtained by two rounds of randomization. As a preparation to the first round, we choose every vertex randomly and uniformly with probability
![]() $p=n^{-0.9}$
to get a random subset R of
$p=n^{-0.9}$
to get a random subset R of
![]() $V(H_{\mathit {\mathbf {G}}})$
. Take
$V(H_{\mathit {\mathbf {G}}})$
. Take
![]() $n^{1.1}$
independent copies of R, and denote them by
$n^{1.1}$
independent copies of R, and denote them by
![]() $R_{i+}$
,
$R_{i+}$
,
![]() $i\in [n^{1.1}]$
, that is each
$i\in [n^{1.1}]$
, that is each
![]() $R_{i+}$
is chosen in the same way as R independently. Define
$R_{i+}$
is chosen in the same way as R independently. Define
![]() $R_{i-}=R_{i+}\setminus S$
for
$R_{i-}=R_{i+}\setminus S$
for
![]() $i\in [n^{1.1}]$
.
$i\in [n^{1.1}]$
.
Fact 1. Let
![]() $n,H_{\textbf {G}}, A, B, S$
, and
$n,H_{\textbf {G}}, A, B, S$
, and
![]() $R_{i-}, R_{i+}$
be given as above. Then, with probability
$R_{i-}, R_{i+}$
be given as above. Then, with probability
![]() $1-o(1)$
, there exist subgraphs
$1-o(1)$
, there exist subgraphs
![]() $R_i, i\in [n^{1.1}]$
, such that
$R_i, i\in [n^{1.1}]$
, such that
![]() $R_{i-}\subseteq R_i \subseteq R_{i+}$
and
$R_{i-}\subseteq R_i \subseteq R_{i+}$
and
![]() $R_i$
is balanced.
$R_i$
is balanced.
The following two lemmas together construct the desired sparse regular k-graph we need.
Lemma 5.3. Given an n-vertex Dk-graph system
![]() $\textbf {G}=\{G_1,\ldots ,G_{nf/b}\}$
on V, let
$\textbf {G}=\{G_1,\ldots ,G_{nf/b}\}$
on V, let
![]() $H_{\textbf {G}}$
be the auxiliary
$H_{\textbf {G}}$
be the auxiliary
![]() $(1,b)$
-graph of
$(1,b)$
-graph of
![]() $\textbf {G}$
. For each
$\textbf {G}$
. For each
![]() $X\subseteq V(H_{\textbf {G}})$
, let
$X\subseteq V(H_{\textbf {G}})$
, let
![]() $Y_X^+:=|\{i:X\subseteq R_{i+}\}|$
and
$Y_X^+:=|\{i:X\subseteq R_{i+}\}|$
and
![]() $Y_X:=|\{i:X\subseteq R_i\}|$
. Let
$Y_X:=|\{i:X\subseteq R_i\}|$
. Let
![]() $\tilde {H}$
be with vertex set
$\tilde {H}$
be with vertex set
![]() $[\frac {nf}{b}]\cup V$
and edge set
$[\frac {nf}{b}]\cup V$
and edge set
![]() $E(\tilde {H})=\{\{i\}\cup e:e\in G_i$
for all
$E(\tilde {H})=\{\{i\}\cup e:e\in G_i$
for all
![]() $i\in [nf/b]\}$
. Then with probability at least
$i\in [nf/b]\}$
. Then with probability at least
![]() $1-o(1)$
, we have
$1-o(1)$
, we have
-
(1)
 $|R_i|=(1/b+1+o(1))n^{0.1}$
for all
$|R_i|=(1/b+1+o(1))n^{0.1}$
for all
 $i\in [n^{1.1}]$
.
$i\in [n^{1.1}]$
. -
(2)
 $Y_{\{v\}}=(1+o(1))n^{0.2}$
for
$Y_{\{v\}}=(1+o(1))n^{0.2}$
for
 $v\in V(H_{\textbf {G}})\setminus S$
and
$v\in V(H_{\textbf {G}})\setminus S$
and
 $Y_{\{v\}}\leq (1+o(1))n^{0.2}$
for
$Y_{\{v\}}\leq (1+o(1))n^{0.2}$
for
 $v\in S$
.
$v\in S$
. -
(3)
 $Y_{\{u,v\}}\leq 2$
for all
$Y_{\{u,v\}}\leq 2$
for all
 $\{u,v\}\subseteq V(H_{\textbf {G}})$
.
$\{u,v\}\subseteq V(H_{\textbf {G}})$
. -
(4)
 $Y_e\leq 1$
for all
$Y_e\leq 1$
for all
 $e\in E(H_{\textbf {G}})$
.
$e\in E(H_{\textbf {G}})$
. -
(5) Suppose that
 $V(R_i)=C_i\cup V_i$
, we have
$V(R_i)=C_i\cup V_i$
, we have
 $\delta _{1,d}(\tilde {H}[\bigcup _{j\in C_i}[(j-1)f+1,jf]\cup V_i])\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /4)\binom {|R_{i+}\cap B|-d}{k-d}-|R_{i+}\cap B\cap S|\binom {|R_{i+}\cap B|-d-1}{k-d-1}\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /8)\binom {|R_i\cap B|-d}{k-d}$
.
$\delta _{1,d}(\tilde {H}[\bigcup _{j\in C_i}[(j-1)f+1,jf]\cup V_i])\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /4)\binom {|R_{i+}\cap B|-d}{k-d}-|R_{i+}\cap B\cap S|\binom {|R_{i+}\cap B|-d-1}{k-d-1}\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /8)\binom {|R_i\cap B|-d}{k-d}$
.
Lemma 5.4. Let
![]() $n, H_{\textbf {G}}, S, R_i$
,
$n, H_{\textbf {G}}, S, R_i$
,
![]() $i\in [n^{1.1}]$
be given as in Lemma 5.3, such that each
$i\in [n^{1.1}]$
be given as in Lemma 5.3, such that each
![]() $H_{\textbf {G}}[R_i]$
is a balanced
$H_{\textbf {G}}[R_i]$
is a balanced
![]() $(1,b)$
-graph and has a perfect fractional matching
$(1,b)$
-graph and has a perfect fractional matching
![]() $\omega _i$
. Then there exists a spanning subgraph
$\omega _i$
. Then there exists a spanning subgraph
![]() $H"$
of
$H"$
of
![]() $H^*=\cup _iH_{\textbf {G}}[R_i]$
, such that
$H^*=\cup _iH_{\textbf {G}}[R_i]$
, such that
-
•
 $d_{H"}(v)\leq (1+o(1))n^{0.2}$
for
$d_{H"}(v)\leq (1+o(1))n^{0.2}$
for
 $v\in S$
,
$v\in S$
, -
•
 $d_{H"}(v)=(1+o(1))n^{0.2}$
for all
$d_{H"}(v)=(1+o(1))n^{0.2}$
for all
 $v\in V(H_{\textbf {G}})\setminus S$
,
$v\in V(H_{\textbf {G}})\setminus S$
, -
•
 $\Delta _2(H")\leq n^{0.1}$
.
$\Delta _2(H")\leq n^{0.1}$
.
The proofs follow the lines as in [Reference Alon, Frankl, Huang, Rödl, Ruciński and Sudakov5, Reference Lo and Markström34, Reference Lu, Wang and Yu36], and thus, we put them in the Appendix.
Proof of Lemma 5.1.
By the definition of
![]() $c_{d,F}^{\mathrm {cov,*}}$
, Lemma 5.3 (5), and Claim 5.2, there exists a perfect fractional matching
$c_{d,F}^{\mathrm {cov,*}}$
, Lemma 5.3 (5), and Claim 5.2, there exists a perfect fractional matching
![]() $\omega _i$
in every subgraph
$\omega _i$
in every subgraph
![]() $H_{\mathit {\mathbf {G}}}[R_i]$
,
$H_{\mathit {\mathbf {G}}}[R_i]$
,
![]() $i\in [n^{1.1}]$
. By Lemma 5.4, there is a spanning subgraph
$i\in [n^{1.1}]$
. By Lemma 5.4, there is a spanning subgraph
![]() $H"$
of
$H"$
of
![]() $H^*=\cup _iH_{\mathit {\mathbf {G}}}[R_i]$
, such that
$H^*=\cup _iH_{\mathit {\mathbf {G}}}[R_i]$
, such that
![]() $d_{H"}(v)\leq (1+o(1))n^{0.2}$
for each
$d_{H"}(v)\leq (1+o(1))n^{0.2}$
for each
![]() $v\in S$
,
$v\in S$
,
![]() $d_{H"}(v)=(1+o(1))n^{0.2}$
for all
$d_{H"}(v)=(1+o(1))n^{0.2}$
for all
![]() $v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
and
$v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
and
![]() $\Delta _2(H")\leq n^{0.1}$
. Hence, by Lemma 3.1 (by setting
$\Delta _2(H")\leq n^{0.1}$
. Hence, by Lemma 3.1 (by setting
![]() $D=n^{0.2}$
),
$D=n^{0.2}$
),
![]() $H"$
contains a cover of at most
$H"$
contains a cover of at most
![]() $\frac {n+n/b}{1+b}(1+a)$
edges which implies that
$\frac {n+n/b}{1+b}(1+a)$
edges which implies that
![]() $H"$
contains a matching of size at least
$H"$
contains a matching of size at least
![]() $\frac {n+n/b}{1+b}(1-a(1+b-1))$
, where a is a constant satisfying
$\frac {n+n/b}{1+b}(1-a(1+b-1))$
, where a is a constant satisfying
![]() $0<a<\phi /(1+b-1)$
. Hence,
$0<a<\phi /(1+b-1)$
. Hence,
![]() $H_{\mathit {\mathbf {G}}}$
contains a matching covering all but at most
$H_{\mathit {\mathbf {G}}}$
contains a matching covering all but at most
![]() $\phi (n+n/b)$
vertices.
$\phi (n+n/b)$
vertices.
6 The proof of Theorem 2.5
Proof. Suppose that
![]() $\frac {1}{n}\ll \phi \ll \gamma _1\ll \gamma \ll \varepsilon '\ll \varepsilon $
, where
$\frac {1}{n}\ll \phi \ll \gamma _1\ll \gamma \ll \varepsilon '\ll \varepsilon $
, where
![]() $\varepsilon ', \gamma $
,
$\varepsilon ', \gamma $
,
![]() $\gamma _1$
are defined in Lemma 4.3 and
$\gamma _1$
are defined in Lemma 4.3 and
![]() $\phi $
,
$\phi $
,
![]() $\varepsilon $
in Lemma 5.1. Let
$\varepsilon $
in Lemma 5.1. Let
![]() $H_{\mathit {\mathbf {G}}}$
be the auxiliary
$H_{\mathit {\mathbf {G}}}$
be the auxiliary
![]() $(1,b)$
-graph of
$(1,b)$
-graph of
![]() $\mathit {\mathbf {G}}$
. By Lemma 4.3, we get a matching M in
$\mathit {\mathbf {G}}$
. By Lemma 4.3, we get a matching M in
![]() $H_{\boldsymbol{G}}$
of size at most
$H_{\boldsymbol{G}}$
of size at most
![]() $2\gamma (m-1)n$
, such that for every balanced set
$2\gamma (m-1)n$
, such that for every balanced set
![]() $U\subseteq [n/b]\cup V\setminus V(M)$
of size at most
$U\subseteq [n/b]\cup V\setminus V(M)$
of size at most
![]() $\gamma _1n$
,
$\gamma _1n$
,
![]() $V(M)\cup U$
spans a matching in
$V(M)\cup U$
spans a matching in
![]() $H_{\mathit {\mathbf {G}}}$
. Let
$H_{\mathit {\mathbf {G}}}$
. Let
![]() $\boldsymbol{G}' =\{G_1^{\prime },\ldots ,G_{nf/b}'\}$
be the induced Dk-graph system of
$\boldsymbol{G}' =\{G_1^{\prime },\ldots ,G_{nf/b}'\}$
be the induced Dk-graph system of
![]() $\boldsymbol{G}$
on
$\boldsymbol{G}$
on
![]() $V'$
, where
$V'$
, where
![]() $V':=V\setminus V(M)$
. Denote the subsystem of
$V':=V\setminus V(M)$
. Denote the subsystem of
![]() $\boldsymbol{G}'$
by
$\boldsymbol{G}'$
by
![]() $\boldsymbol{G}^{\prime }_I=\{G_i'\mid i\in I=[nf/b]\backslash \bigcup _{j\in V(M)\cap [n/b]}[(j-1)f+1,jf]\}$
. We still have
$\boldsymbol{G}^{\prime }_I=\{G_i'\mid i\in I=[nf/b]\backslash \bigcup _{j\in V(M)\cap [n/b]}[(j-1)f+1,jf]\}$
. We still have
![]() $\delta _d(G_i')\geq (\max \{c_{d,F}^{\mathrm {abs,*}},c_{d,F}^{\mathrm {cov,*}}\}+\frac {\varepsilon }{2})\binom {n-d}{k-d}$
for
$\delta _d(G_i')\geq (\max \{c_{d,F}^{\mathrm {abs,*}},c_{d,F}^{\mathrm {cov,*}}\}+\frac {\varepsilon }{2})\binom {n-d}{k-d}$
for
![]() $i\in I$
, since
$i\in I$
, since
![]() $2\gamma (m-1) n\binom {n-d-1}{k-d-1}\leq \frac {\varepsilon }{2}\binom {n-d}{k-d}$
. Then, we construct the new auxiliary
$2\gamma (m-1) n\binom {n-d-1}{k-d-1}\leq \frac {\varepsilon }{2}\binom {n-d}{k-d}$
. Then, we construct the new auxiliary
![]() $(1,b)$
-graph
$(1,b)$
-graph
![]() $H_{\boldsymbol{G}_I^{\prime }}$
of
$H_{\boldsymbol{G}_I^{\prime }}$
of
![]() $\boldsymbol{G}_I^{\prime }$
.
$\boldsymbol{G}_I^{\prime }$
.
By Lemma 5.1,
![]() $H_{\boldsymbol{G}_I^{\prime }}$
contains a matching
$H_{\boldsymbol{G}_I^{\prime }}$
contains a matching
![]() $M_1$
covering all but at most
$M_1$
covering all but at most
![]() $\phi |V'|\leq \phi (n+n/b)$
vertices. Suppose
$\phi |V'|\leq \phi (n+n/b)$
vertices. Suppose
![]() $W_1=[n/b]\cup V\setminus (V(M)\cup V(M_1))$
, hence,
$W_1=[n/b]\cup V\setminus (V(M)\cup V(M_1))$
, hence,
![]() $|W_1|\leq \phi (n+n/b)\leq \gamma _1n$
and
$|W_1|\leq \phi (n+n/b)\leq \gamma _1n$
and
![]() $W_1$
is balanced. By Lemma 4.3,
$W_1$
is balanced. By Lemma 4.3,
![]() $V(M)\cup W_1$
spans a matching
$V(M)\cup W_1$
spans a matching
![]() $M_2$
in
$M_2$
in
![]() $H_{\mathit {\mathbf {G}}}$
and therefore
$H_{\mathit {\mathbf {G}}}$
and therefore
![]() $M_1\cup M_2$
is a perfect matching in
$M_1\cup M_2$
is a perfect matching in
![]() $H_{\mathit {\mathbf {G}}}$
, which yields a rainbow F-factor in
$H_{\mathit {\mathbf {G}}}$
, which yields a rainbow F-factor in
![]() $\boldsymbol{G}$
.
$\boldsymbol{G}$
.
In the next few sections, we prove our results in Section 1 (Theorems 1.4 – 1.7), and by Theorem 2.5, it suffices to specify the
![]() $\delta _d^*$
we use and bound the parameters
$\delta _d^*$
we use and bound the parameters
![]() $c_{d,F}^{\mathrm { abs,*}}$
and
$c_{d,F}^{\mathrm { abs,*}}$
and
![]() $c_{d,F}^{\mathrm {cov,*}}$
. Note also that we will not present a proof of Theorem 1.3, as it follows from either of the two directed extensions.
$c_{d,F}^{\mathrm {cov,*}}$
. Note also that we will not present a proof of Theorem 1.3, as it follows from either of the two directed extensions.
7 The proofs of Theorems 1.4 and 1.5
For Theorem 1.4, to apply Theorem 2.5, we set
![]() $\delta _1^*$
as the minimum out-degree
$\delta _1^*$
as the minimum out-degree
![]() $\delta ^+$
. Given that
$\delta ^+$
. Given that
![]() $\delta ^+(D_i)\geq (1-\frac {1}{k}+\varepsilon )n$
for
$\delta ^+(D_i)\geq (1-\frac {1}{k}+\varepsilon )n$
for
![]() $i\in [\frac {n}{k}\binom {k}{2}]$
, by Theorem 2.5, it remains to prove that
$i\in [\frac {n}{k}\binom {k}{2}]$
, by Theorem 2.5, it remains to prove that
![]() $c_{1,T_k}^{\mathrm {abs,+}}, c_{1,T_k}^{\mathrm {cov,+}}\leq 1-\frac {1}{k}$
.
$c_{1,T_k}^{\mathrm {abs,+}}, c_{1,T_k}^{\mathrm {cov,+}}\leq 1-\frac {1}{k}$
.
Similarly, for Theorem 1.5, we set
![]() $\delta _1^*$
as the minimum semidegree
$\delta _1^*$
as the minimum semidegree
![]() $\delta ^0$
. Given
$\delta ^0$
. Given
![]() $T\in \mathcal T_k$
and
$T\in \mathcal T_k$
and
![]() $\delta ^0(D_i)\geq (1-\frac {1}{k}+\varepsilon )n$
for
$\delta ^0(D_i)\geq (1-\frac {1}{k}+\varepsilon )n$
for
![]() $i\in [\frac {n}{k}\binom {k}{2}]$
, by Theorem 2.5, it remains to prove that
$i\in [\frac {n}{k}\binom {k}{2}]$
, by Theorem 2.5, it remains to prove that
![]() $c_{1,T}^{\mathrm {abs,0}}, c_{1,T}^{\mathrm {cov,0}}\leq 1-\frac {1}{k}$
.
$c_{1,T}^{\mathrm {abs,0}}, c_{1,T}^{\mathrm {cov,0}}\leq 1-\frac {1}{k}$
.
Since the proofs are similar, we only show that
![]() $c_{1,T_k}^{\mathrm {abs,+}}, c_{1,T_k}^{\mathrm {cov,+}}\leq 1-\frac {1}{k}$
for Theorem 1.4. Recall that
$c_{1,T_k}^{\mathrm {abs,+}}, c_{1,T_k}^{\mathrm {cov,+}}\leq 1-\frac {1}{k}$
for Theorem 1.4. Recall that
![]() $T_k$
is the transitive tournament on k vertices. Note that
$T_k$
is the transitive tournament on k vertices. Note that
![]() $c_{1,T_k}^{\mathrm {abs,+}}\leq 1-\frac {1}{k}$
is exactly (1).
$c_{1,T_k}^{\mathrm {abs,+}}\leq 1-\frac {1}{k}$
is exactly (1).
We partition the n-vertex digraph system
![]() $\mathit {\mathbf {D}}$
into
$\mathit {\mathbf {D}}$
into
![]() $[n/k]$
subsystems
$[n/k]$
subsystems
![]() $\mathit {\mathbf {D}}_1,\ldots ,\mathit {\mathbf {D}}_{n/k}$
, where
$\mathit {\mathbf {D}}_1,\ldots ,\mathit {\mathbf {D}}_{n/k}$
, where
![]() $\mathit {\mathbf {D}}_i=\{D_{(i-1)\binom {k}{2}+1},\ldots ,D_{i\binom {k}{2}}\}$
. Define
$\mathit {\mathbf {D}}_i=\{D_{(i-1)\binom {k}{2}+1},\ldots ,D_{i\binom {k}{2}}\}$
. Define
![]() $H_{T_k, i}$
as the k-graph which consists of rainbow copies of
$H_{T_k, i}$
as the k-graph which consists of rainbow copies of
![]() $T_k$
on
$T_k$
on
![]() $\mathit {\mathbf {D}}_i$
with color set
$\mathit {\mathbf {D}}_i$
with color set
![]() $[(i-1)\binom {k}{2}+1,i\binom {k}{2}]$
. We shall show that each
$[(i-1)\binom {k}{2}+1,i\binom {k}{2}]$
. We shall show that each
![]() $H_{T_k, i}$
has a perfect fractional matching.
$H_{T_k, i}$
has a perfect fractional matching.
Claim 7.1. For
![]() $i\in [n/k]$
,
$i\in [n/k]$
,
![]() $H_{T_k, i}$
has a perfect fractional matching.
$H_{T_k, i}$
has a perfect fractional matching.
A k-complex is a hypergraph J, such that every edge of J has size at most k,
![]() $\emptyset \in J$
and is closed under inclusion, that is if
$\emptyset \in J$
and is closed under inclusion, that is if
![]() $e \in J$
and
$e \in J$
and
![]() $e'\subseteq e$
, then
$e'\subseteq e$
, then
![]() $e' \in J$
. We refer to the edges of size r in J as r-edges of J and write
$e' \in J$
. We refer to the edges of size r in J as r-edges of J and write
![]() $J_r$
to denote the r-graph on
$J_r$
to denote the r-graph on
![]() $V(J)$
formed by these edges. We introduce the following notion of degree in a k-system J. For any edge e of J, the degree
$V(J)$
formed by these edges. We introduce the following notion of degree in a k-system J. For any edge e of J, the degree
![]() $d(e)$
of e is the number of (
$d(e)$
of e is the number of (
![]() $|e|$
+1)-edges
$|e|$
+1)-edges
![]() $e'$
of J which contains e as a subset (note that this is not the standard notion of degree used in k-graphs, in which the degree of a set is the number of edges containing it). The minimum r-degree of J, denoted by
$e'$
of J which contains e as a subset (note that this is not the standard notion of degree used in k-graphs, in which the degree of a set is the number of edges containing it). The minimum r-degree of J, denoted by
![]() $\delta _r(J)$
, is the minimum of
$\delta _r(J)$
, is the minimum of
![]() $d(e)$
taken over all r-edges
$d(e)$
taken over all r-edges
![]() $e\in J$
. Trivially,
$e\in J$
. Trivially,
![]() $\delta _0(J)=|V(J)|$
. So every r-edge of J is contained in at least
$\delta _0(J)=|V(J)|$
. So every r-edge of J is contained in at least
![]() $\delta _r(J)$
(
$\delta _r(J)$
(
![]() $r+1$
)-edges of J. The degree sequence of J is
$r+1$
)-edges of J. The degree sequence of J is
Lemma 7.2 (Lemma 3.6, [Reference Joos and Kim23]).
If the complex J satisfies
![]() $\delta (J)\geq (n, \frac {k-1}{k}n, \frac {k-2}{k}n,\ldots , \frac {1}{k}n)$
, then
$\delta (J)\geq (n, \frac {k-1}{k}n, \frac {k-2}{k}n,\ldots , \frac {1}{k}n)$
, then
![]() $J_k$
contains a perfect fractional matching.
$J_k$
contains a perfect fractional matching.
To prove Claim 7.1, we construct the clique k-complex
![]() $J^i$
for each
$J^i$
for each
![]() $\boldsymbol{D}_i$
,
$\boldsymbol{D}_i$
,
![]() $i\in [n/k]$
, which has vertex set V and edge set
$i\in [n/k]$
, which has vertex set V and edge set
![]() $E(J^i_r)$
, where each edge is a rainbow
$E(J^i_r)$
, where each edge is a rainbow
![]() $T_r$
with color set
$T_r$
with color set
![]() $[(i-1)\binom {k}{2}+1, (i-1)\binom {k}{2}+\binom {r}{2}]$
for each
$[(i-1)\binom {k}{2}+1, (i-1)\binom {k}{2}+\binom {r}{2}]$
for each
![]() $r\in [k]$
and
$r\in [k]$
and
![]() $i\in [n/k]$
. Note that for each i, the top level
$i\in [n/k]$
. Note that for each i, the top level
![]() $J_k^i$
is exactly
$J_k^i$
is exactly
![]() $H_{T_k, i}$
. By the out-degree condition, we get
$H_{T_k, i}$
. By the out-degree condition, we get
Therefore, Claim 7.1 follows from Lemma 7.2, and we are done.
For completeness, we include the short proof of Lemma 7.2 given in [Reference Joos and Kim23]. Given points
![]() $\mathbf {x}_1,\ldots ,\mathbf {x}_s\in \mathbb {R}^d$
, we define their positive cone as
$\mathbf {x}_1,\ldots ,\mathbf {x}_s\in \mathbb {R}^d$
, we define their positive cone as
![]() $PC(\textbf {x}_1,\ldots ,\textbf {x}_s):=\{\sum _{j\in [s]}\lambda _j\textbf {x}_j:\lambda _1,\ldots ,\lambda _s\geq 0\}$
. Recall that V is the n-vertex set, for any
$PC(\textbf {x}_1,\ldots ,\textbf {x}_s):=\{\sum _{j\in [s]}\lambda _j\textbf {x}_j:\lambda _1,\ldots ,\lambda _s\geq 0\}$
. Recall that V is the n-vertex set, for any
![]() $S\subseteq V$
, the characteristic vector
$S\subseteq V$
, the characteristic vector
![]() $\chi (S)$
of S is the binary vector in
$\chi (S)$
of S is the binary vector in
![]() $\mathbb {R}^n$
, such that
$\mathbb {R}^n$
, such that
![]() $\chi (S)_i=1$
if and only if
$\chi (S)_i=1$
if and only if
![]() $i\in S$
. Given a k-graph H, if H has a perfect fractional matching
$i\in S$
. Given a k-graph H, if H has a perfect fractional matching
![]() $\omega $
, then
$\omega $
, then
![]() $\textbf {1}\in PC(\chi (e):e\in H)$
, since
$\textbf {1}\in PC(\chi (e):e\in H)$
, since
![]() $\sum _{e\in H}\omega (e)\chi (e)=\textbf {1}$
. The well-known Farkas’ lemma reads as follows.
$\sum _{e\in H}\omega (e)\chi (e)=\textbf {1}$
. The well-known Farkas’ lemma reads as follows.
Lemma 7.3 (Farkas’ lemma).
Suppose
![]() $\textbf {v}\in \mathbb {R}^n\backslash PC(Y)$
for some finite set
$\textbf {v}\in \mathbb {R}^n\backslash PC(Y)$
for some finite set
![]() $Y\subseteq \mathbb {R}^n$
. Then there is some
$Y\subseteq \mathbb {R}^n$
. Then there is some
![]() $\textbf {a}\in \mathbb {R}^n$
, such that
$\textbf {a}\in \mathbb {R}^n$
, such that
![]() $\textbf {a}\cdot \textbf {y}\geq 0$
for every
$\textbf {a}\cdot \textbf {y}\geq 0$
for every
![]() $\textbf {y}\in Y$
and
$\textbf {y}\in Y$
and
![]() $\textbf {a}\cdot \textbf {v}<0$
.
$\textbf {a}\cdot \textbf {v}<0$
.
Proof of Lemma 7.2.
Suppose that
![]() $J_k$
does not contain a perfect fractional matching, this means that
$J_k$
does not contain a perfect fractional matching, this means that
![]() $\textbf {1}\notin PC(\chi (e):e\in J_k)$
. Then, by Lemma 7.3, there is some
$\textbf {1}\notin PC(\chi (e):e\in J_k)$
. Then, by Lemma 7.3, there is some
![]() $\textbf {a}\in \mathbb {R}^n$
, such that
$\textbf {a}\in \mathbb {R}^n$
, such that
![]() $\textbf {a}\cdot \textbf {1}<0$
and
$\textbf {a}\cdot \textbf {1}<0$
and
![]() $\textbf {a}\cdot \chi (e)\geq 0$
for every
$\textbf {a}\cdot \chi (e)\geq 0$
for every
![]() $e\in J_k$
. Let
$e\in J_k$
. Let
![]() $V=\{v_1,\ldots ,v_n\}$
and
$V=\{v_1,\ldots ,v_n\}$
and
![]() $\textbf {a}=(a_1,\ldots ,a_n)$
, satisfying
$\textbf {a}=(a_1,\ldots ,a_n)$
, satisfying
![]() $a_1\leq a_2\leq \cdots \leq a_n$
.
$a_1\leq a_2\leq \cdots \leq a_n$
.
We first build a k-edge
![]() $e=\{v_{d_1},\ldots ,v_{d_k}\}\in J_k$
, such that
$e=\{v_{d_1},\ldots ,v_{d_k}\}\in J_k$
, such that
![]() $d_j\le \frac {j-1}kn+1, j\in [k]$
as follows. Choose
$d_j\le \frac {j-1}kn+1, j\in [k]$
as follows. Choose
![]() $d_1=1$
and, having chosen
$d_1=1$
and, having chosen
![]() $d_1,\dots , d_j$
, the choice of
$d_1,\dots , d_j$
, the choice of
![]() $d_{j+1}$
is guaranteed by
$d_{j+1}$
is guaranteed by
![]() $\delta _j(J)\ge (1-j/k)n$
. As
$\delta _j(J)\ge (1-j/k)n$
. As
![]() $e\in J_k$
, we have
$e\in J_k$
, we have
![]() $\textbf {a}\cdot \chi (e)\ge 0$
. Consider
$\textbf {a}\cdot \chi (e)\ge 0$
. Consider
![]() $\{S_i=\{v_i,v_{i+n/k},\ldots ,v_{i+(k-1)n/k}\}:i\in [n/k]\}$
which form a partition of V, thus
$\{S_i=\{v_i,v_{i+n/k},\ldots ,v_{i+(k-1)n/k}\}:i\in [n/k]\}$
which form a partition of V, thus
![]() $\sum _{i\in [n/k]}\textbf {a}\cdot \chi (S_i)=\textbf {a}\cdot \textbf {1}<0$
. However, as the indices of vertices of e precede those of
$\sum _{i\in [n/k]}\textbf {a}\cdot \chi (S_i)=\textbf {a}\cdot \textbf {1}<0$
. However, as the indices of vertices of e precede those of
![]() $S_i$
one-by-one and
$S_i$
one-by-one and
![]() $a_1\leq a_2\leq \cdots \leq a_n$
, we have for each i,
$a_1\leq a_2\leq \cdots \leq a_n$
, we have for each i,
![]() $\textbf {a}\cdot \chi (S_i)\ge \textbf {a}\cdot \chi (e)\ge 0$
, a contradiction.
$\textbf {a}\cdot \chi (S_i)\ge \textbf {a}\cdot \chi (e)\ge 0$
, a contradiction.
8 The proof of Theorem 1.6
For Theorem 1.6, we set
![]() $\delta _1^*$
as the minimum partite-degree
$\delta _1^*$
as the minimum partite-degree
![]() $\delta '$
. Let
$\delta '$
. Let
![]() $\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{n\binom {k}{2}}\}$
be a collection of k-partite graphs with a common partition
$\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{n\binom {k}{2}}\}$
be a collection of k-partite graphs with a common partition
![]() $V_1,\ldots ,V_k$
, each of size n, such that
$V_1,\ldots ,V_k$
, each of size n, such that
![]() $\delta '(G_i)\geq (1-1/k+\varepsilon )n$
for
$\delta '(G_i)\geq (1-1/k+\varepsilon )n$
for
![]() $i\in [n\binom {k}{2}]$
. By Theorem 2.5, it remains to prove that
$i\in [n\binom {k}{2}]$
. By Theorem 2.5, it remains to prove that
![]() $c_{1, K_k}^{\mathrm {abs,'}}, c_{1,K_k}^{\mathrm {cov,'}}\leq 1-\frac {1}{k}$
. The conclusion that
$c_{1, K_k}^{\mathrm {abs,'}}, c_{1,K_k}^{\mathrm {cov,'}}\leq 1-\frac {1}{k}$
. The conclusion that
![]() $c_{1,K_k}^{\mathrm {abs,'}}\leq 1-\frac {1}{k}$
can be similarly derived as (1) in Section 4.2.1 and thus omitted. We next show how to obtain
$c_{1,K_k}^{\mathrm {abs,'}}\leq 1-\frac {1}{k}$
can be similarly derived as (1) in Section 4.2.1 and thus omitted. We next show how to obtain
![]() $c_{1,K_k}^{\mathrm {cov,'}}\leq 1-\frac {1}{k}$
.
$c_{1,K_k}^{\mathrm {cov,'}}\leq 1-\frac {1}{k}$
.
Let H be a k-graph, and let
![]() $\mathcal {P}$
be a partition of
$\mathcal {P}$
be a partition of
![]() $V(H)$
. Then we say a set
$V(H)$
. Then we say a set
![]() $S\subseteq V(H)$
is k-partite if it has one vertex in any part of
$S\subseteq V(H)$
is k-partite if it has one vertex in any part of
![]() $\mathcal {P}$
, and that H is k-partite if every edge of H is k-partite. Let V be a set of vertices, let
$\mathcal {P}$
, and that H is k-partite if every edge of H is k-partite. Let V be a set of vertices, let
![]() $\mathcal {P}$
be a partition of V into k parts
$\mathcal {P}$
be a partition of V into k parts
![]() $V_1,\ldots , V_k$
, and let J be a k-partite k-system on V. For each
$V_1,\ldots , V_k$
, and let J be a k-partite k-system on V. For each
![]() $0\leq j\leq k-1$
, we define the partite minimum j-degree
$0\leq j\leq k-1$
, we define the partite minimum j-degree
![]() $\delta ^*_j(J)$
as the largest m, such that any j-edge e has at least m extensions to a
$\delta ^*_j(J)$
as the largest m, such that any j-edge e has at least m extensions to a
![]() $(j+1)$
-edge in any part not used by e, that is
$(j+1)$
-edge in any part not used by e, that is
The partite degree sequence is
![]() $\delta ^*(J)=(\delta ^*_0(J),\ldots ,\delta ^*_{k-1}(J))$
.
$\delta ^*(J)=(\delta ^*_0(J),\ldots ,\delta ^*_{k-1}(J))$
.
To obtain
![]() $c_{1,K_k}^{\mathrm {cov,'}}$
, we use the following lemma, which is a special case of [Reference Joos and Kim23, Lemma 7.2]. Again we present the short proof of Lemma 8.1 given in [Reference Joos and Kim23].
$c_{1,K_k}^{\mathrm {cov,'}}$
, we use the following lemma, which is a special case of [Reference Joos and Kim23, Lemma 7.2]. Again we present the short proof of Lemma 8.1 given in [Reference Joos and Kim23].
Lemma 8.1. Let V be a set partitioned into k parts
![]() $V_1,\ldots ,V_k$
, each of size n, and let J be a k-partite k-system on V, such that
$V_1,\ldots ,V_k$
, each of size n, and let J be a k-partite k-system on V, such that
 $$\begin{align*}\delta^*(J)\geq \left(n, \frac{(k-1)n}{k},\frac{(k-2)n}{k},\ldots,\frac{n}{k} \right).\end{align*}$$
$$\begin{align*}\delta^*(J)\geq \left(n, \frac{(k-1)n}{k},\frac{(k-2)n}{k},\ldots,\frac{n}{k} \right).\end{align*}$$
Then
![]() $J_k$
contains a perfect fractional matching.
$J_k$
contains a perfect fractional matching.
Proof. Suppose that
![]() $J_k$
does not contain a perfect fractional matching, this means that
$J_k$
does not contain a perfect fractional matching, this means that
![]() $\textbf {1}\notin PC(\chi (e):e\in J_k)$
. Then, by Lemma 7.3, there is some
$\textbf {1}\notin PC(\chi (e):e\in J_k)$
. Then, by Lemma 7.3, there is some
![]() $\textbf {a}\in \mathbb {R}^{kn}$
, such that
$\textbf {a}\in \mathbb {R}^{kn}$
, such that
![]() $\textbf {a}\cdot \textbf {1}<0$
and
$\textbf {a}\cdot \textbf {1}<0$
and
![]() $\textbf {a}\chi (e)\geq 0$
for every
$\textbf {a}\chi (e)\geq 0$
for every
![]() $e\in J_k$
. Let
$e\in J_k$
. Let
![]() $V=\{v_{1,1},\ldots ,v_{1,n},v_{2,1},\ldots ,v_{2,n},\ldots ,v_{k,1},\ldots ,v_{k,n}\}$
and
$V=\{v_{1,1},\ldots ,v_{1,n},v_{2,1},\ldots ,v_{2,n},\ldots ,v_{k,1},\ldots ,v_{k,n}\}$
and
satisfying that
![]() $a_{j,\frac {(j-1)n}{k}+1}\leq \cdots \leq a_{j,n}\leq a_{j,1}\leq \ldots \leq a_{j,\frac {(j-1)n}{k}}$
for each
$a_{j,\frac {(j-1)n}{k}+1}\leq \cdots \leq a_{j,n}\leq a_{j,1}\leq \ldots \leq a_{j,\frac {(j-1)n}{k}}$
for each
![]() $j\in [k]$
.
$j\in [k]$
.
We first build a k-edge
![]() $e=\{v_{1,d_1},v_{2,d_2}\ldots ,v_{k,d_k}\}\in J_k$
, such that
$e=\{v_{1,d_1},v_{2,d_2}\ldots ,v_{k,d_k}\}\in J_k$
, such that
![]() $d_j\le \frac {j-1}kn+1, j\in [k]$
as follows. Choose
$d_j\le \frac {j-1}kn+1, j\in [k]$
as follows. Choose
![]() $d_1=1$
and, having chosen
$d_1=1$
and, having chosen
![]() $d_1,\dots , d_j$
, the choice of
$d_1,\dots , d_j$
, the choice of
![]() $d_{j+1}$
is guaranteed by
$d_{j+1}$
is guaranteed by
![]() $\delta _j(J)\ge (1-j/k)n$
. As
$\delta _j(J)\ge (1-j/k)n$
. As
![]() $e\in J_k$
, we have
$e\in J_k$
, we have
![]() $\textbf {a}\cdot \chi (e)\ge 0$
. Consider
$\textbf {a}\cdot \chi (e)\ge 0$
. Consider
![]() $\{S_i=\{v_{1,i},v_{2,i},\ldots ,v_{k,i}\}:i\in [n]\}$
which forms a partition of V, thus
$\{S_i=\{v_{1,i},v_{2,i},\ldots ,v_{k,i}\}:i\in [n]\}$
which forms a partition of V, thus
![]() $\sum _{i\in [n]}\textbf {a}\cdot \chi (S_i)=\textbf {a}\cdot \textbf {1}<0$
. However, we have for each i,
$\sum _{i\in [n]}\textbf {a}\cdot \chi (S_i)=\textbf {a}\cdot \textbf {1}<0$
. However, we have for each i,
![]() $\textbf {a}\cdot \chi (S_i)\ge \textbf {a}\cdot \chi (e)\ge 0$
, as
$\textbf {a}\cdot \chi (S_i)\ge \textbf {a}\cdot \chi (e)\ge 0$
, as
![]() $a_{j,\frac {(j-1)n}{k}+1}\leq \cdots \leq a_{j,n}\leq a_{j,1}\leq \ldots \leq a_{j,\frac {(j-1)n}{k}}$
for each
$a_{j,\frac {(j-1)n}{k}+1}\leq \cdots \leq a_{j,n}\leq a_{j,1}\leq \ldots \leq a_{j,\frac {(j-1)n}{k}}$
for each
![]() $j\in [k]$
, a contradiction.
$j\in [k]$
, a contradiction.
We partition the
![]() $kn$
-vertex k-partite graph system
$kn$
-vertex k-partite graph system
![]() $\mathit {\mathbf {G}}$
on V into n subsystems
$\mathit {\mathbf {G}}$
on V into n subsystems
![]() $\mathit {\mathbf {G}}_1,\ldots ,\mathit {\mathbf {G}}_{n}$
, where
$\mathit {\mathbf {G}}_1,\ldots ,\mathit {\mathbf {G}}_{n}$
, where
![]() $\mathit {\mathbf {G}}_i=\{G_{(i-1)\binom {k}{2}+1},\ldots ,G_{i\binom {k}{2}}\}$
for
$\mathit {\mathbf {G}}_i=\{G_{(i-1)\binom {k}{2}+1},\ldots ,G_{i\binom {k}{2}}\}$
for
![]() $i\in [n]$
. The clique k-complex
$i\in [n]$
. The clique k-complex
![]() $J^i$
of a k-partite graph system
$J^i$
of a k-partite graph system
![]() $\boldsymbol{G}_i$
is with vertex set V and edge set
$\boldsymbol{G}_i$
is with vertex set V and edge set
![]() $E(J^i_r)$
, where each edge is a rainbow
$E(J^i_r)$
, where each edge is a rainbow
![]() $K_r$
with color set
$K_r$
with color set
![]() $[(i-1)\binom {k}{2}+1,(i-1)\binom {k}{2}+\binom {r}{2}]$
for each
$[(i-1)\binom {k}{2}+1,(i-1)\binom {k}{2}+\binom {r}{2}]$
for each
![]() $r\in [k]$
and
$r\in [k]$
and
![]() $i\in [n]$
. In
$i\in [n]$
. In
![]() $\mathit {\mathbf {G}}$
, by the degree condition, we get for each
$\mathit {\mathbf {G}}$
, by the degree condition, we get for each
![]() $i\in [n]$
,
$i\in [n]$
,
 $$\begin{align*}\delta^*(J^i)\geq \left(n,\left(1-\frac{1}{k}+\varepsilon\right)n,\ldots,\left(\frac{1}{k}+\varepsilon\right)n\right). \end{align*}$$
$$\begin{align*}\delta^*(J^i)\geq \left(n,\left(1-\frac{1}{k}+\varepsilon\right)n,\ldots,\left(\frac{1}{k}+\varepsilon\right)n\right). \end{align*}$$
By Lemma 8.1,
![]() $J_k^i$
contains a perfect fractional matching. Therefore,
$J_k^i$
contains a perfect fractional matching. Therefore,
![]() $c_{1,K_k}^{\mathrm {cov,'}}\leq 1-\frac {1}{k}$
.
$c_{1,K_k}^{\mathrm {cov,'}}\leq 1-\frac {1}{k}$
.
9 The proof of Theorem 1.7
Note that
![]() $c_{d,F}^{\mathrm {{abs},d}}\leq \frac {1}{2}$
is given in (2). By Definition 2.4, we trivially have
$c_{d,F}^{\mathrm {{abs},d}}\leq \frac {1}{2}$
is given in (2). By Definition 2.4, we trivially have
![]() $c_{d,F}^{\mathrm {{cov},d}}\leq c_{k,d}$
, where F is an edge. By Theorem 2.5, the proof of Theorem 1.7 is completed.
$c_{d,F}^{\mathrm {{cov},d}}\leq c_{k,d}$
, where F is an edge. By Theorem 2.5, the proof of Theorem 1.7 is completed.
10 Concluding remarks
In this paper, we studied the rainbow version of clique-factor problems in graph and hypergraph systems. The most desirable question is to prove an exact version of the rainbow Hajnal–Szemerédi theorem, which we put as a conjecture here.
Conjecture 10.1. Let
![]() $\textbf {G}=\{G_1, G_2,\ldots , G_{\frac {n}{t}\binom {t}{2}}\}$
be an n-vertex graph system. If
$\textbf {G}=\{G_1, G_2,\ldots , G_{\frac {n}{t}\binom {t}{2}}\}$
be an n-vertex graph system. If
![]() $\delta (G_i)\geq (1-\frac {1}{t})n$
for
$\delta (G_i)\geq (1-\frac {1}{t})n$
for
![]() $i\in [\frac {n}{t}\binom {t}{2}]$
, then
$i\in [\frac {n}{t}\binom {t}{2}]$
, then
![]() $\textbf {G}$
contains a rainbow
$\textbf {G}$
contains a rainbow
![]() $K_t$
-factor.
$K_t$
-factor.
Appendix A The postponed proofs
Below, we restate and prove Fact 1 and Lemmas 5.3 and 5.4.
Fact 1. Let
![]() $n,H_{\mathit {\mathbf {G}}},A,B,S$
and
$n,H_{\mathit {\mathbf {G}}},A,B,S$
and
![]() $R_{i-}, R_{i+}$
be given as above. Then, with probability
$R_{i-}, R_{i+}$
be given as above. Then, with probability
![]() $1-o(1)$
, there exist subgraphs
$1-o(1)$
, there exist subgraphs
![]() $R_i, i\in [n^{1.1}]$
, such that
$R_i, i\in [n^{1.1}]$
, such that
![]() $R_{i-}\subseteq R_i \subseteq R_{i+}$
and
$R_{i-}\subseteq R_i \subseteq R_{i+}$
and
![]() $R_i$
is balanced.
$R_i$
is balanced.
Proof. Recall that
![]() $|A|=n/b, |B|=n, |S\cap A|=n^{0.99}/b$
and
$|A|=n/b, |B|=n, |S\cap A|=n^{0.99}/b$
and
![]() $|S\cap B|=n^{0.99}$
, thus
$|S\cap B|=n^{0.99}$
, thus
 $$\begin{align*}\mathbb{E}[|R_{i+}\cap A|]&=n^{0.1}/b,\\\mathbb{E}[|R_{i+}\cap A\cap S|]7&=n^{0.09}/b,\\\mathbb{E}[|R_{i+}\cap B|]&=n^{0.1},\\\mathbb{E}[|R_{i+}\cap B\cap S|]77&=n^{0.09}.\end{align*}$$
$$\begin{align*}\mathbb{E}[|R_{i+}\cap A|]&=n^{0.1}/b,\\\mathbb{E}[|R_{i+}\cap A\cap S|]7&=n^{0.09}/b,\\\mathbb{E}[|R_{i+}\cap B|]&=n^{0.1},\\\mathbb{E}[|R_{i+}\cap B\cap S|]77&=n^{0.09}.\end{align*}$$
By Lemma 3.2, we have
 $$\begin{align*}\mathbb{P}[||R_{i+}\cap A|-n^{0.1}/b|\geq n^{0.08}]&\leq e^{-\Omega(n^{0.06})},\\\mathbb{P}[||R_{i+}\cap A\cap S|-n^{0.09}/b|\geq n^{0.08}]&\leq e^{-\Omega(n^{0.07})},\\\mathbb{P}[||R_{i+}\cap B|-n^{0.1}|\geq n^{0.08}]&\leq e^{-\Omega(n^{0.06})},\\\mathbb{P}[||R_{i+}\cap B\cap S|-n^{0.09}/b|\geq n^{0.08}]&\leq e^{-\Omega(n^{0.07})}.\end{align*}$$
$$\begin{align*}\mathbb{P}[||R_{i+}\cap A|-n^{0.1}/b|\geq n^{0.08}]&\leq e^{-\Omega(n^{0.06})},\\\mathbb{P}[||R_{i+}\cap A\cap S|-n^{0.09}/b|\geq n^{0.08}]&\leq e^{-\Omega(n^{0.07})},\\\mathbb{P}[||R_{i+}\cap B|-n^{0.1}|\geq n^{0.08}]&\leq e^{-\Omega(n^{0.06})},\\\mathbb{P}[||R_{i+}\cap B\cap S|-n^{0.09}/b|\geq n^{0.08}]&\leq e^{-\Omega(n^{0.07})}.\end{align*}$$
Thus, with probability
![]() $1-o(1)$
, for all
$1-o(1)$
, for all
![]() $i\in [n^{1.1}]$
,
$i\in [n^{1.1}]$
,
 $$\begin{align*}|R_{i+}\cap A|\in[n^{0.1}/b&-n^{0.08},n^{0.1}/b+n^{0.08}],\\|R_{i+}\cap A\cap S|&=(1+o(1))n^{0.09}/b,\\|R_{i+}\cap B|\in[n^{0.1}&-n^{0.08},n^{0.1}+n^{0.08}],\\|R_{i+}\cap B\cap S|&=(1+o(1))n^{0.09}.\end{align*}$$
$$\begin{align*}|R_{i+}\cap A|\in[n^{0.1}/b&-n^{0.08},n^{0.1}/b+n^{0.08}],\\|R_{i+}\cap A\cap S|&=(1+o(1))n^{0.09}/b,\\|R_{i+}\cap B|\in[n^{0.1}&-n^{0.08},n^{0.1}+n^{0.08}],\\|R_{i+}\cap B\cap S|&=(1+o(1))n^{0.09}.\end{align*}$$
Therefore,
![]() $|b|R_{i+}\cap A|-|R_{i+}\cap B||\leq (b+1)n^{0.08}<\min \{|R_{i+}\cap A\cap S|,|R_{i+}\cap B\cap S|\}$
. Hence, with probability
$|b|R_{i+}\cap A|-|R_{i+}\cap B||\leq (b+1)n^{0.08}<\min \{|R_{i+}\cap A\cap S|,|R_{i+}\cap B\cap S|\}$
. Hence, with probability
![]() $1-o(1)$
,
$1-o(1)$
,
![]() $R_i$
can be balanced for
$R_i$
can be balanced for
![]() $i\in [n^{1.1}]$
.
$i\in [n^{1.1}]$
.
Lemma 5.3. Given an n-vertex Dk-graph system
![]() $\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{nf/b}\}$
on V, let
$\mathit {\mathbf {G}}=\{G_1,\ldots ,G_{nf/b}\}$
on V, let
![]() $H_{\mathit {\mathbf {G}}}$
be the auxiliary
$H_{\mathit {\mathbf {G}}}$
be the auxiliary
![]() $(1,b)$
-graph of
$(1,b)$
-graph of
![]() $\mathit {\mathbf {G}}$
. For each
$\mathit {\mathbf {G}}$
. For each
![]() $X\subseteq V(H_{\mathit {\mathbf {G}}})$
, let
$X\subseteq V(H_{\mathit {\mathbf {G}}})$
, let
![]() $Y_X^+:=|\{i:X\subseteq R_{i+}\}|$
and
$Y_X^+:=|\{i:X\subseteq R_{i+}\}|$
and
![]() $Y_X:=|\{i:X\subseteq R_i\}|$
. Let
$Y_X:=|\{i:X\subseteq R_i\}|$
. Let
![]() $\tilde {H}$
be with vertex set
$\tilde {H}$
be with vertex set
![]() $[\frac {nf}{b}]\cup V$
and edge set
$[\frac {nf}{b}]\cup V$
and edge set
![]() $E(\tilde {H})=\{\{i\}\cup e:e\in G_i$
for all
$E(\tilde {H})=\{\{i\}\cup e:e\in G_i$
for all
![]() $i\in [nf/b]\}$
. Then, with probability at least
$i\in [nf/b]\}$
. Then, with probability at least
![]() $1-o(1)$
, we have
$1-o(1)$
, we have
-
(1)
 $|R_i|=(1/b+1+o(1))n^{0.1}$
for all
$|R_i|=(1/b+1+o(1))n^{0.1}$
for all
 $i\in [n^{1.1}]$
.
$i\in [n^{1.1}]$
. -
(2)
 $Y_{\{v\}}=(1+o(1))n^{0.2}$
for
$Y_{\{v\}}=(1+o(1))n^{0.2}$
for
 $v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
, and
$v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
, and
 $Y_{\{v\}}\leq (1+o(1))n^{0.2}$
for
$Y_{\{v\}}\leq (1+o(1))n^{0.2}$
for
 $v\in S$
.
$v\in S$
. -
(3)
 $Y_{\{u,v\}}\leq 2$
for all
$Y_{\{u,v\}}\leq 2$
for all
 $\{u,v\}\subseteq V(H_{\mathit {\mathbf {G}}})$
.
$\{u,v\}\subseteq V(H_{\mathit {\mathbf {G}}})$
. -
(4)
 $Y_e\leq 1$
for all
$Y_e\leq 1$
for all
 $e\in E(H_{\mathit {\mathbf {G}}})$
.
$e\in E(H_{\mathit {\mathbf {G}}})$
. -
(5) Suppose that
 $V(R_i)=C_i\cup V_i$
, we have
$V(R_i)=C_i\cup V_i$
, we have
 $\delta _{1,d}(\tilde {H}[\bigcup _{j\in C_i}[(j-1)f+1,jf]\cup V_i])\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /4)\binom {|R_{i+}\cap B|-d}{k-d}-|R_{i+}\cap B\cap S|\binom {|R_{i+}\cap B|-d-1}{k-d-1}\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /8)\binom {|R_i\cap B|-d}{k-d}$
.
$\delta _{1,d}(\tilde {H}[\bigcup _{j\in C_i}[(j-1)f+1,jf]\cup V_i])\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /4)\binom {|R_{i+}\cap B|-d}{k-d}-|R_{i+}\cap B\cap S|\binom {|R_{i+}\cap B|-d-1}{k-d-1}\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /8)\binom {|R_i\cap B|-d}{k-d}$
.
Proof. Note that
![]() $\mathbb {E}[|R_{i+}|]=(1/b+1)n^{0.1}, \mathbb {E}[|R_{i-}|]=((1/b+1)n-(1/b+1)n^{0.99})n^{-0.9}=(1/b+1)n^{0.1}-(1/b+1)n^{0.09}$
. By Lemma 3.2, we have
$\mathbb {E}[|R_{i+}|]=(1/b+1)n^{0.1}, \mathbb {E}[|R_{i-}|]=((1/b+1)n-(1/b+1)n^{0.99})n^{-0.9}=(1/b+1)n^{0.1}-(1/b+1)n^{0.09}$
. By Lemma 3.2, we have
 $$\begin{align*}\mathbb{P}[\mid|R_{i+}|-n^{0.1}(1/b+1)\mid\geq n^{0.095}]&\leq e^{-\Omega(n^{0.09})},\\\mathbb{P}[\mid|R_{i-}|-((1/b+1)n^{0.1}-(1/b+1)n^{0.09})\mid&\geq n^{0.095}]\leq e^{-\Omega(n^{0.09})}.\end{align*}$$
$$\begin{align*}\mathbb{P}[\mid|R_{i+}|-n^{0.1}(1/b+1)\mid\geq n^{0.095}]&\leq e^{-\Omega(n^{0.09})},\\\mathbb{P}[\mid|R_{i-}|-((1/b+1)n^{0.1}-(1/b+1)n^{0.09})\mid&\geq n^{0.095}]\leq e^{-\Omega(n^{0.09})}.\end{align*}$$
Hence, with probability at least
![]() $1-O(n^{1.1})e^{-\Omega (n^{0.09})}$
, for the given sequence
$1-O(n^{1.1})e^{-\Omega (n^{0.09})}$
, for the given sequence
![]() $R_i$
in Fact 1,
$R_i$
in Fact 1,
![]() $i\in [n^{1.1}]$
, satisfying
$i\in [n^{1.1}]$
, satisfying
![]() $R_{i-}\subseteq R_i \subseteq R_{i+}$
, we have
$R_{i-}\subseteq R_i \subseteq R_{i+}$
, we have
![]() $|R_i|=(1/b+1+o(1))n^{0.1}$
.
$|R_i|=(1/b+1+o(1))n^{0.1}$
.
For each
![]() $X\subseteq V(H_{\mathit {\mathbf {G}}})$
, let
$X\subseteq V(H_{\mathit {\mathbf {G}}})$
, let
![]() $Y_X^+:=|\{i:X\subseteq R_{i+}\}|$
and
$Y_X^+:=|\{i:X\subseteq R_{i+}\}|$
and
![]() $Y_X:=|\{i:X\subseteq R_i\}|$
. Note that the random variables
$Y_X:=|\{i:X\subseteq R_i\}|$
. Note that the random variables
![]() $Y_X^+$
have binomial distributions
$Y_X^+$
have binomial distributions
![]() $Bi(n^{1.1},n^{-0.9|X|})$
with expectations
$Bi(n^{1.1},n^{-0.9|X|})$
with expectations
![]() $n^{1.1-0.9|X|}$
and
$n^{1.1-0.9|X|}$
and
![]() $Y_X\leq Y_X^+$
. In particular, for each
$Y_X\leq Y_X^+$
. In particular, for each
![]() $v\in V(H_{\mathit {\mathbf {G}}})$
,
$v\in V(H_{\mathit {\mathbf {G}}})$
,
![]() $\mathbb {E}[Y_{\{v\}}^+]=n^{0.2}$
, by Lemma 3.2, we have
$\mathbb {E}[Y_{\{v\}}^+]=n^{0.2}$
, by Lemma 3.2, we have
Hence, with probability at least
![]() $1-O(n)e^{-\Omega (n^{0.18})}$
, we have
$1-O(n)e^{-\Omega (n^{0.18})}$
, we have
![]() $Y_{\{v\}}=(1+o(1))n^{0.2}$
for
$Y_{\{v\}}=(1+o(1))n^{0.2}$
for
![]() $v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
and
$v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
and
![]() $Y_{\{v\}}\leq (1+o(1))n^{0.2}$
for
$Y_{\{v\}}\leq (1+o(1))n^{0.2}$
for
![]() $v\in S$
.
$v\in S$
.
Let
![]() $Z_{p,q}=|X\in \binom {V(H_{\mathit {\mathbf {G}}})}{p}:Y_X^+\geq q|$
. Then,
$Z_{p,q}=|X\in \binom {V(H_{\mathit {\mathbf {G}}})}{p}:Y_X^+\geq q|$
. Then,
 $$\begin{align*}\mathbb{E}[Z_{p,q}]\leq\binom{\frac{n}{b}+n}{p}\binom{n^{1.1}}{q}(n^{-0.9pq})\leq Cn^{p+1.1q-0.9pq}.\end{align*}$$
$$\begin{align*}\mathbb{E}[Z_{p,q}]\leq\binom{\frac{n}{b}+n}{p}\binom{n^{1.1}}{q}(n^{-0.9pq})\leq Cn^{p+1.1q-0.9pq}.\end{align*}$$
Hence, by Markov’s Inequality, we have
 $$\begin{align*}\mathbb{P}[Z_{2,3}=0]=1-\mathbb{P}[Z_{2,3}\geq1]&\geq1-\mathbb{E}[Z_{2,3}]=1-o(1),\\\mathbb{P}[Z_{1+b,2}=0]=1-\mathbb{P}[Z_{1+b,2}\geq1]&\geq1-\mathbb{E}[Z_{1+b,2}]=1-o(1),\end{align*}$$
$$\begin{align*}\mathbb{P}[Z_{2,3}=0]=1-\mathbb{P}[Z_{2,3}\geq1]&\geq1-\mathbb{E}[Z_{2,3}]=1-o(1),\\\mathbb{P}[Z_{1+b,2}=0]=1-\mathbb{P}[Z_{1+b,2}\geq1]&\geq1-\mathbb{E}[Z_{1+b,2}]=1-o(1),\end{align*}$$
that is with probability at least
![]() $1-o(1)$
, every pair
$1-o(1)$
, every pair
![]() $\{u,v\}\subseteq V(H_{\mathit {\mathbf {G}}})$
is contained in at most two sets
$\{u,v\}\subseteq V(H_{\mathit {\mathbf {G}}})$
is contained in at most two sets
![]() $R_{i+}$
, and every edge is contained in at most one set
$R_{i+}$
, and every edge is contained in at most one set
![]() $R_{i+}$
. Thus, the conclusions also hold for
$R_{i+}$
. Thus, the conclusions also hold for
![]() $R_i$
.
$R_i$
.
Fix a
![]() $(1,d)$
-subset
$(1,d)$
-subset
![]() $D\subseteq V(\tilde {H})$
, and let
$D\subseteq V(\tilde {H})$
, and let
![]() $N_D(\tilde {H})$
be the neighborhood of D in
$N_D(\tilde {H})$
be the neighborhood of D in
![]() $\tilde {H}$
. Recall that R is obtained by choosing every vertex randomly and uniformly with probability
$\tilde {H}$
. Recall that R is obtained by choosing every vertex randomly and uniformly with probability
![]() $p=n^{-0.9}$
, let
$p=n^{-0.9}$
, let
![]() $DEG_D$
be the number of edges
$DEG_D$
be the number of edges
![]() $\{f|f\subseteq R$
and
$\{f|f\subseteq R$
and
![]() $f\in N_D(\tilde {H})\}$
. Therefore,
$f\in N_D(\tilde {H})\}$
. Therefore,
![]() $DEG_D=\sum _{f\in N_D(\tilde {H})}X_f$
, where
$DEG_D=\sum _{f\in N_D(\tilde {H})}X_f$
, where
![]() $X_f=1$
if f is in R and 0 otherwise. We have
$X_f=1$
if f is in R and 0 otherwise. We have
 $$\begin{align*}\mathbb{E}[DEG_D]&=d_{\tilde{H}}(D)\times(n^{-0.9})^{k-d} \geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon)\binom{n-d}{k-d}n^{-0.9(k-d)}\\&\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/3) \binom{|R\cap B|-d}{k-d}=\Omega(n^{0.1(k-d)}).\end{align*}$$
$$\begin{align*}\mathbb{E}[DEG_D]&=d_{\tilde{H}}(D)\times(n^{-0.9})^{k-d} \geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon)\binom{n-d}{k-d}n^{-0.9(k-d)}\\&\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/3) \binom{|R\cap B|-d}{k-d}=\Omega(n^{0.1(k-d)}).\end{align*}$$
For two distinct intersecting edges
![]() $f_i,f_j\in N_D(\tilde {H})$
with
$f_i,f_j\in N_D(\tilde {H})$
with
![]() $|f_i\cap f_j|=\ell $
for
$|f_i\cap f_j|=\ell $
for
![]() $\ell \in [k-d-1]$
, the probability that both of them are in R is
$\ell \in [k-d-1]$
, the probability that both of them are in R is
for any fixed
![]() $\ell $
, we have
$\ell $
, we have
 $$\begin{align*}\Delta&=\sum_{f_i\cap f_j\neq\emptyset}\mathbb{P}[X_{f_i}=X_{f_j}=1]\leq\sum_{\ell=1}^{k-d-1}p^{2(k-d)-\ell}\binom{n-d}{k-d}\binom{k-d}{\ell}\binom{n-k}{k-d-\ell}\\&\leq\sum_{\ell=1}^{k-d-1}p^{2(k-d)-\ell}O(n^{2(k-d)-\ell})=O(n^{0.1(2(k-d)-1)}).\end{align*}$$
$$\begin{align*}\Delta&=\sum_{f_i\cap f_j\neq\emptyset}\mathbb{P}[X_{f_i}=X_{f_j}=1]\leq\sum_{\ell=1}^{k-d-1}p^{2(k-d)-\ell}\binom{n-d}{k-d}\binom{k-d}{\ell}\binom{n-k}{k-d-\ell}\\&\leq\sum_{\ell=1}^{k-d-1}p^{2(k-d)-\ell}O(n^{2(k-d)-\ell})=O(n^{0.1(2(k-d)-1)}).\end{align*}$$
Applying Lemma 3.4 with
![]() $\Gamma =B$
,
$\Gamma =B$
,
![]() $\Gamma _p=R\cap B$
, and
$\Gamma _p=R\cap B$
, and
![]() $M=N_{\tilde {H}}(D)$
(a family of
$M=N_{\tilde {H}}(D)$
(a family of
![]() $(k-d)$
-sets), we have
$(k-d)$
-sets), we have
Therefore, by the union bound, with probability
![]() $1-o(1)$
, for all
$1-o(1)$
, for all
![]() $(1,d)$
-subsets
$(1,d)$
-subsets
![]() $D\subseteq V(\tilde {H})$
, we have
$D\subseteq V(\tilde {H})$
, we have
 $$\begin{align*}DEG_D>(1-\varepsilon/12)\mathbb{E}[DEG_D]\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/4)\binom{|R\cap B|-d}{k-d}.\end{align*}$$
$$\begin{align*}DEG_D>(1-\varepsilon/12)\mathbb{E}[DEG_D]\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/4)\binom{|R\cap B|-d}{k-d}.\end{align*}$$
Summarizing, with probability
![]() $1-o(1)$
, for the sequence
$1-o(1)$
, for the sequence
![]() $R_i, i\in [n^{1.1}]$
, satisfying
$R_i, i\in [n^{1.1}]$
, satisfying
![]() $R_{i-}\subseteq R_i \subseteq R_{i+}$
, all of the following hold.
$R_{i-}\subseteq R_i \subseteq R_{i+}$
, all of the following hold.
-
(1)
 $|R_i|=(1/b+1+o(1))n^{0.1}$
for all
$|R_i|=(1/b+1+o(1))n^{0.1}$
for all
 $i\in [n^{1.1}]$
.
$i\in [n^{1.1}]$
. -
(2)
 $Y_{\{v\}}=(1+o(1))n^{0.2}$
for
$Y_{\{v\}}=(1+o(1))n^{0.2}$
for
 $v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
, and
$v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
, and
 $Y_{\{v\}}\leq (1+o(1))n^{0.2}$
for
$Y_{\{v\}}\leq (1+o(1))n^{0.2}$
for
 $v\in S$
.
$v\in S$
. -
(3)
 $Y_{\{u,v\}}\leq 2$
for all
$Y_{\{u,v\}}\leq 2$
for all
 $\{u,v\}\subseteq V(H_{\mathit {\mathbf {G}}})$
.
$\{u,v\}\subseteq V(H_{\mathit {\mathbf {G}}})$
. -
(4)
 $Y_e\leq 1$
for all
$Y_e\leq 1$
for all
 $e\in E(H_{\mathit {\mathbf {G}}})$
.
$e\in E(H_{\mathit {\mathbf {G}}})$
. -
(5)
 $DEG_D^{(i)}\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /4)\binom {|R_{i+}\cap B|-d}{k-d}$
for all
$DEG_D^{(i)}\geq (c_{d,F}^{\mathrm {cov,*}}+\varepsilon /4)\binom {|R_{i+}\cap B|-d}{k-d}$
for all
 $(1,d)$
-subsets of
$(1,d)$
-subsets of
 $D\subseteq V(\tilde {H})$
and
$D\subseteq V(\tilde {H})$
and
 $i\in [n^{1.1}]$
.
$i\in [n^{1.1}]$
.
Thus, by Property (5) above, we conclude that suppose
![]() $V(R_i^+)=C_i^+\cup V_i^+$
and
$V(R_i^+)=C_i^+\cup V_i^+$
and
![]() $V(R_i)=C_i\cup V_i$
, the following holds.
$V(R_i)=C_i\cup V_i$
, the following holds.
 $$\begin{align*}\delta_{1,d}(\tilde{H}[\bigcup_{j\in C_i^+}[(j-1)f+1,jf]\cup V_i^+]])\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/4)\binom{|R_{i+}\cap B|-d}{k-d}.\end{align*}$$
$$\begin{align*}\delta_{1,d}(\tilde{H}[\bigcup_{j\in C_i^+}[(j-1)f+1,jf]\cup V_i^+]])\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/4)\binom{|R_{i+}\cap B|-d}{k-d}.\end{align*}$$
After the modification, we still have
 $$\begin{align*}\delta_{1,d}(\tilde{H}[\bigcup_{j\in C_i}[(j-1)f+1,jf]\cup V_i]])&\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/4)\binom{|R_{i+}\cap B|-d}{k-d}-|R_{i+}\cap B\cap S|\binom{|R_{i+}\cap B|-d-1}{k-d-1}\\&\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/8)\binom{|R_i\cap B|-d}{k-d}.\\[-34pt]\end{align*}$$
$$\begin{align*}\delta_{1,d}(\tilde{H}[\bigcup_{j\in C_i}[(j-1)f+1,jf]\cup V_i]])&\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/4)\binom{|R_{i+}\cap B|-d}{k-d}-|R_{i+}\cap B\cap S|\binom{|R_{i+}\cap B|-d-1}{k-d-1}\\&\geq(c_{d,F}^{\mathrm{cov,*}}+\varepsilon/8)\binom{|R_i\cap B|-d}{k-d}.\\[-34pt]\end{align*}$$
Lemma 5.4. Let
![]() $n, H_{\mathit {\mathbf {G}}}, S, R_i$
,
$n, H_{\mathit {\mathbf {G}}}, S, R_i$
,
![]() $i\in [n^{1.1}]$
be given as in Lemma 5.3, such that each
$i\in [n^{1.1}]$
be given as in Lemma 5.3, such that each
![]() $H_{\mathit {\mathbf {G}}}[R_i]$
is a balanced
$H_{\mathit {\mathbf {G}}}[R_i]$
is a balanced
![]() $(1,b)$
-graph and has a perfect fractional matching
$(1,b)$
-graph and has a perfect fractional matching
![]() $\omega _i$
. Then there exists a spanning subgraph
$\omega _i$
. Then there exists a spanning subgraph
![]() $H"$
of
$H"$
of
![]() $H^*=\cup _iH_{\mathit {\mathbf {G}}}[R_i]$
, such that
$H^*=\cup _iH_{\mathit {\mathbf {G}}}[R_i]$
, such that
-
•
 $d_{H"}(v)\leq (1+o(1))n^{0.2}$
for
$d_{H"}(v)\leq (1+o(1))n^{0.2}$
for
 $v\in S$
,
$v\in S$
, -
•
 $d_{H"}(v)=(1+o(1))n^{0.2}$
for all
$d_{H"}(v)=(1+o(1))n^{0.2}$
for all
 $v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
,
$v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
, -
•
 $\Delta _2(H")\leq n^{0.1}$
.
$\Delta _2(H")\leq n^{0.1}$
.
Proof. By the condition that each
![]() $H_{\mathit {\mathbf {G}}}[R_i]$
has a perfect fractional matching
$H_{\mathit {\mathbf {G}}}[R_i]$
has a perfect fractional matching
![]() $\omega _i$
, we select a generalized binomial subgraph
$\omega _i$
, we select a generalized binomial subgraph
![]() $H"$
of
$H"$
of
![]() $H^*$
by independently choosing each edge e with probability
$H^*$
by independently choosing each edge e with probability
![]() $\omega _{i_e}(e)$
, where
$\omega _{i_e}(e)$
, where
![]() $i_e$
is the index i, such that
$i_e$
is the index i, such that
![]() $e\in H_{\mathit {\mathbf {G}}}[R_i]$
. Recall that Property (4) guarantees the uniqueness of
$e\in H_{\mathit {\mathbf {G}}}[R_i]$
. Recall that Property (4) guarantees the uniqueness of
![]() $i_e$
.
$i_e$
.
For
![]() $v\in V(H")$
, let
$v\in V(H")$
, let
![]() $I_v=\{i:v\in R_i\}$
,
$I_v=\{i:v\in R_i\}$
,
![]() $E_v=\{e\in H^*:v\in e\}$
, and
$E_v=\{e\in H^*:v\in e\}$
, and
![]() $E_v^i=E_v\cap H_{\mathit {\mathbf {G}}}[R_i]$
, then
$E_v^i=E_v\cap H_{\mathit {\mathbf {G}}}[R_i]$
, then
![]() $E_v^i, i\in I_v$
forms a partition of
$E_v^i, i\in I_v$
forms a partition of
![]() $E_v$
and
$E_v$
and
![]() $|I_v|=Y_{\{v\}}$
. Hence, for
$|I_v|=Y_{\{v\}}$
. Hence, for
![]() $v\in V(H")$
,
$v\in V(H")$
,
 $$\begin{align*}d_{H"}(v)=\sum_{e\in E_v}1=\sum_{i\in I_v}\sum_{e\in E_v^i}X_e,\end{align*}$$
$$\begin{align*}d_{H"}(v)=\sum_{e\in E_v}1=\sum_{i\in I_v}\sum_{e\in E_v^i}X_e,\end{align*}$$
where
![]() $X_e$
is the Bernoulli random variable with
$X_e$
is the Bernoulli random variable with
![]() $X_e=1$
if
$X_e=1$
if
![]() $e\in E(H")$
and
$e\in E(H")$
and
![]() $X_e=0$
otherwise. Thus, its expectation is
$X_e=0$
otherwise. Thus, its expectation is
![]() $\omega _{i_e}(e)$
. Therefore
$\omega _{i_e}(e)$
. Therefore
 $$\begin{align*}\mathbb{E}[d_{H"}(v)]=\sum_{i\in I_v}\sum_{e\in E_v^i}\omega_{i_e}(e)=\sum_{i\in I_v}1=Y_{\{v\}}.\end{align*}$$
$$\begin{align*}\mathbb{E}[d_{H"}(v)]=\sum_{i\in I_v}\sum_{e\in E_v^i}\omega_{i_e}(e)=\sum_{i\in I_v}1=Y_{\{v\}}.\end{align*}$$
Hence,
![]() $\mathbb {E}[d_{H"}(v)]=(1+o(1))n^{0.2}$
for
$\mathbb {E}[d_{H"}(v)]=(1+o(1))n^{0.2}$
for
![]() $v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
and
$v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
and
![]() $\mathbb {E}[d_{H"}(v)]\leq (1+o(1))n^{0.2}$
for
$\mathbb {E}[d_{H"}(v)]\leq (1+o(1))n^{0.2}$
for
![]() $v\in S$
. Now by Chernoff’s inequality, for
$v\in S$
. Now by Chernoff’s inequality, for
![]() $v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
,
$v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
,
and for
![]() $v\in S$
,
$v\in S$
,
Taking a union bound over all vertices, we conclude that, with probability
![]() $1-o(1)$
,
$1-o(1)$
,
![]() $d_{H"}(v)=(1+o(1))n^{0.2}$
for all
$d_{H"}(v)=(1+o(1))n^{0.2}$
for all
![]() $v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
and
$v\in V(H_{\mathit {\mathbf {G}}})\setminus S$
and
![]() $d_{H"}(v)\leq (1+o(1))n^{0.2}$
for
$d_{H"}(v)\leq (1+o(1))n^{0.2}$
for
![]() $v\in S$
.
$v\in S$
.
Next, note that for distinct
![]() $u,v\in V(H_{\mathit {\mathbf {G}}})$
,
$u,v\in V(H_{\mathit {\mathbf {G}}})$
,
 $$\begin{align*}d_{H"}(\{u,v\})=\sum_{e\in E_u\cap E_v}1=\sum_{i\in I_u\cap I_v}\sum_{e\in E_u^i\cap E_v^i}X_e,\end{align*}$$
$$\begin{align*}d_{H"}(\{u,v\})=\sum_{e\in E_u\cap E_v}1=\sum_{i\in I_u\cap I_v}\sum_{e\in E_u^i\cap E_v^i}X_e,\end{align*}$$
and
 $$\begin{align*}\mathbb{E}[d_{H"}(\{u,v\})]=\sum_{i\in I_u\cap I_v}\sum_{e\in E_u^i\cap E_v^i}\omega_i(e)\leq|I_u\cap I_v|\leq2.\end{align*}$$
$$\begin{align*}\mathbb{E}[d_{H"}(\{u,v\})]=\sum_{i\in I_u\cap I_v}\sum_{e\in E_u^i\cap E_v^i}\omega_i(e)\leq|I_u\cap I_v|\leq2.\end{align*}$$
Thus, by Lemma 3.3,
then by a union bound, we have
![]() $\Delta _2(H")\leq n^{0.1}$
with probability
$\Delta _2(H")\leq n^{0.1}$
with probability
![]() $1-o(1)$
.
$1-o(1)$
.
Acknowledgement
We thank the anonymous referees for detailed feedback that improved the presentation of the paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
Guanghui Wang is supported by the Natural Science Foundation of China (12231018) and Young Taishan Scholars Program of Shandong Province.
Notes added in the proof
Soon after this manuscript was released, Montgomery, Müyesser and Pehova [Reference Treglown44] independently proved more general results, that is, they determined asymptotically optimal minimum degree conditions for F-factor transversals and spanning tree transversals in graph systems.