No CrossRef data available.
Article contents
KMS states on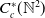 
$C_c^{*}(\mathbb{N}^2)$
Published online by Cambridge University Press: 03 April 2023
Abstract
Let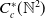 
$C_c^{*}(\mathbb{N}^{2})$ be the universal 
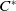$C^{*}$-algebra generated by a semigroup of isometries 
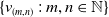$\{v_{(m,n)}\,:\, m,n \in \mathbb{N}\}$ whose range projections commute. We analyse the structure of KMS states on 
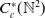$C_{c}^{*}(\mathbb{N}^2)$ for the time evolution determined by a homomorphism 
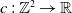$c\,:\,\mathbb{Z}^{2} \to \mathbb{R}$. In contrast to the reduced version 
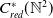$C_{red}^{*}(\mathbb{N}^{2})$, we show that the set of KMS states on 
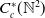$C_{c}^{*}(\mathbb{N}^{2})$ has a rich structure. In particular, we exhibit uncountably many extremal KMS states of type I, II and III.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust
References
Aaronson, J, An introduction to infinite ergodic theory, Mathematical Surveys and Monographs, vol. 50 (American Mathematical Society, Providence, RI, 1997).Google Scholar
Aaronson, J, Nakada, H, Sarig, O and Solomyak, R, Invariant measures and asymptotics for some skew products, Israel J. Math 128 (2002), 93–134.Google Scholar
Björklund, M, Z. Kosloff, and S. Vaes, Ergodicity and type of nonsingular Bernoulli actions, Invent. Math. 224(2) (2021), 573–625.Google Scholar
Brownlowe, N, Larsen, N. S., Ramagge, J and Stammeier, N, C
$^{*}$
-algebras of right LCM monoids and their equilibrium states, Trans. Amer. Math. Soc. 373(7) (2020), 5235–5273.Google Scholar
$^{*}$
-algebras of right LCM monoids and their equilibrium states, Trans. Amer. Math. Soc. 373(7) (2020), 5235–5273.Google ScholarChristensen, Johannes and Thomsen, Klaus, KMS states on the crossed product C
$^{*}$
-algebra of a homeomorphism,
Ergodic Theory Dynam. Syst. 42(4) (2022), 1373–1414.Google Scholar
$^{*}$
-algebra of a homeomorphism,
Ergodic Theory Dynam. Syst. 42(4) (2022), 1373–1414.Google ScholarCuntz, J, C
$^{*}$
-algebras associated with the
$ax+b$
-semigroup over
$\mathbb{N}$
, K-theory and noncommutative geometry, EMS Ser. Congr. Rep. (2008), 201–215. Available at https://mathscinet.ams.org/mathscinet/search/publications.html?fmt=bibtex&pg1=MR&s1=2513338
Google Scholar
$^{*}$
-algebras associated with the
$ax+b$
-semigroup over
$\mathbb{N}$
, K-theory and noncommutative geometry, EMS Ser. Congr. Rep. (2008), 201–215. Available at https://mathscinet.ams.org/mathscinet/search/publications.html?fmt=bibtex&pg1=MR&s1=2513338
Google ScholarCuntz, J, Deninger, C and Laca, M, C
$^{*}$
-algebras of Toeplitz type associated with algebraic number fields, Math. Ann 355(4) (2013), 1383–1423.Google Scholar
$^{*}$
-algebras of Toeplitz type associated with algebraic number fields, Math. Ann 355(4) (2013), 1383–1423.Google ScholarCuntz, J, Echterhoff, S and Li, X, On the
$K$
-theory of crossed products by automorphic semigroup actions, Q J. Math. 64(3) (2013), 747–784.Google Scholar
$K$
-theory of crossed products by automorphic semigroup actions, Q J. Math. 64(3) (2013), 747–784.Google ScholarCuntz, J and Li, X, The regular C*-algebra of an integral domain, Quanta of maths, Clay math. proc, vol. 11 (Amer. Math. Soc., Providence, RI, 2010), 149–170.Google Scholar
Cuntz, J and Li, X, C
$^*$
-algebras associated with integral domains and crossed products by actions on adele spaces, J. Noncommut. Geom. 5(1) (2011), 1–37.Google Scholar
$^*$
-algebras associated with integral domains and crossed products by actions on adele spaces, J. Noncommut. Geom. 5(1) (2011), 1–37.Google ScholarDanilenko, A. I. and Silva, C. E., Ergodic theory: non-singular transformations, Mathematics of complexity and dynamical systems, Vols. 1-3 (Springer, Newyork, 2012), 329–356.CrossRefGoogle Scholar
Hamachi, T, On a Bernoulli shift with nonidentical factor measures, Ergodic Theory Dynam. Syst. 1(3) (1981), 273–283, 1982.Google Scholar
Katznelson, Y., Sigma-finite invariant measures for smooth mappings of the circle, J. Anal. Math. 31 (1997), 1–18.Google Scholar
Laca, M and Neshveyev, S, Type
$III_1$
equilibrium states of the Toeplitz algebra of the affine semigroup over the natural numbers, J. Funct. Anal. 261(1) (2011), 169–187.Google Scholar
$III_1$
equilibrium states of the Toeplitz algebra of the affine semigroup over the natural numbers, J. Funct. Anal. 261(1) (2011), 169–187.Google ScholarLaca, M and Raeburn, I, Phase transition on the Toeplitz algebra of the affine semigroup over the natural numbers, Adv. Math. 225(2) (2010), 643–688.Google Scholar
Li, X, Semigroup C
$^{*}$
-algebras and amenability of semigroups, J. Funct. Anal. 262(10) (2012), 4302–4340.Google Scholar
$^{*}$
-algebras and amenability of semigroups, J. Funct. Anal. 262(10) (2012), 4302–4340.Google ScholarLi, X, Nuclearity of semigroup C
$^{*}$
-algebras and the connection to amenability, Adv. Math. 244 (2013), 626–662.Google Scholar
$^{*}$
-algebras and the connection to amenability, Adv. Math. 244 (2013), 626–662.Google ScholarMuhly, P. S. and Renault, J. N., C
$^{*}$
-algebras of multivariable Wiener-Hopf operators, Trans. Amer. Math. Soc. 274(1) (1982), 1–44.Google Scholar
$^{*}$
-algebras of multivariable Wiener-Hopf operators, Trans. Amer. Math. Soc. 274(1) (1982), 1–44.Google ScholarMurphy, G. J., C
$^{*}$
-algebras generated by commuting isometries, Rocky Mountain J. Math. 26(1) (1996), 237–267.Google Scholar
$^{*}$
-algebras generated by commuting isometries, Rocky Mountain J. Math. 26(1) (1996), 237–267.Google ScholarNakada, H, Piecewise linear homeomorphisms of type III and the ergodicity of cylinder flows, Keio Math. Sem. Rep.
7 (1982), 29–40. Available at https://mathscinet.ams.org/mathscinet/search/publications.html?fmt=bibtex&pg1=MR&s1=667804
Google Scholar
Nakada, H, On a classification of PL-homeomorphisms of a circle, Probability theory and mathematical statistics (Tbilisi, 1982), Lecture Notes in Math, vol. 1021 (Springer, Berlin, 1983), 474–480.Google Scholar
Neshveyev, S, KMS states on the C
$^{*}$
-algebras of non-principal groupoids, J. Operator Theory 70(2) (2013), 513–530.CrossRefGoogle Scholar
$^{*}$
-algebras of non-principal groupoids, J. Operator Theory 70(2) (2013), 513–530.CrossRefGoogle ScholarRaeburn, I and Vittadello, S. T., The isometric representation theory of a perforated semigroup, J. Operator Theory 62(2) (2009), 357–370.Google Scholar
Salas, H. N., Semigroups of isometries with commuting range projections, J. Operator Theory 14(2) (1985), 311–346.Google Scholar
Sundar, S., C
$^{*}$
-algebras associated to topological Ore semigroups, Münster J. Math. 9(1) (2016), 155–185.Google Scholar
$^{*}$
-algebras associated to topological Ore semigroups, Münster J. Math. 9(1) (2016), 155–185.Google ScholarVittadello, S. T., The isometric representation theory of numerical semigroups, Integral Equations Operator Theory 64(4) (2009), 573–597.Google Scholar