Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-06-12T07:34:34.290Z Has data issue: false hasContentIssue false
  • English
  • Français

A first-passage-place problem for integrated diffusion processes

Part of: Markov processes

Published online by Cambridge University Press:  22 May 2023

Mario Lefebvre
Mario Lefebvre*
Affiliation:
Polytechnique Montréal
*
*Postal address: Department of Mathematics and Industrial Engineering, Polytechnique Montréal, C.P. 6079, Succursale Centre-ville, Montréal, Québec H3C 3A7, Canada. Email: mlefebvre@polymtl.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 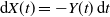${\mathrm{d}} X(t) = -Y(t) \, {\mathrm{d}} t$, where Y(t) is a one-dimensional diffusion process, and let 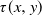$\tau(x,y)$ be the first time the process (X(t), Y(t)), starting from (x, y), leaves a subset of the first quadrant. The problem of computing the probability 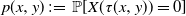$p(x,y)\,:\!=\, \mathbb{P}[X(\tau(x,y))=0]$ is considered. The Laplace transform of the function p(x, y) is obtained in important particular cases, and it is shown that the transform can at least be inverted numerically. Explicit expressions for the Laplace transform of 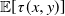$\mathbb{E}[\tau(x,y)]$ and of the moment-generating function of 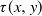$\tau(x,y)$ can also be derived.

Keywords

First-passage timeBrownian motionKolmogorov backward equationLaplace transform

MSC classification

Primary: 60J60: Diffusion processes
Secondary: 60J70: Applications of Brownian motions and diffusion theory (population genetics, absorption problems, etc.)
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 1 , March 2024 , pp. 55 - 67
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (1965). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York.Google Scholar
Abundo, A. (2016). On the first-passage time of an integrated Gauss–Markov process. Sci. Math. Jpn. 79, 175–188.Google Scholar
Abundo, A. (2017). The mean of the running maximum of an integrated Gauss–Markov process and the connection with its first-passage time. Stoch. Anal. Appl. 35, 499–510.CrossRefGoogle Scholar
Atkinson, R. A. and Clifford, P. (1994). The escape probability for integrated Brownian motion with non-zero drift. J. Appl. Prob. 31, 921–929.CrossRefGoogle Scholar
Cox, D. R. and Miller, H. D. (1965). The Theory of Stochastic Processes. Methuen, London.Google Scholar
Ghamlouch, H., Grall, A. and Fouladirad, M. (2015). On the use of jump-diffusion process for maintenance decision-making: A first step. In Proc. Annual Reliability and Maintainability Symp. (RAMS).CrossRefGoogle Scholar
Goldman, M. (1971). On the first passage of the integrated Wiener process. Ann. Math. Stat. 42, 2150–2155.CrossRefGoogle Scholar
Gor’kov, J. P. (1975). A formula for the solution of a certain boundary value problem for the stationary equation of Brownian motion. Dokl. Akad. Nauk SSSR 223, 525–528 (in Russian).Google Scholar
Hesse, C. H. (2005). On the first-passage time of integrated Brownian motion. J. Appl. Math. Stoch. Anal. 2005, 237–246.CrossRefGoogle Scholar
Karlin, S. and Taylor, H. M. (1981). A Second Course in Stochastic Processes. Academic Press, New York.Google Scholar
Lachal, A. (1991). Sur le premier instant de passage de l’intégrale du mouvement brownien. Ann. Inst. H. Poincaré Prob. Statist. 27, 385–405.Google Scholar
Lefebvre, M. (1989). First-passage densities of a two-dimensional process. SIAM J. Appl. Math. 49, 1514–1523.CrossRefGoogle Scholar
Lefebvre, M. (2020). Analytical solution to an LQG homing problem in two dimensions. ITM Web of Conferences 34, 01003.CrossRefGoogle Scholar
Lefebvre, M. (2020). Maximizing the expected remaining useful lifetime of a weakly controlled device. Eng. Optim. 52, 1588–1597.CrossRefGoogle Scholar
McKean, H. P. Jr. (1963). A winding problem for a resonator driven by a white noise. J. Math. Kyoto Univ. 2, 227–235.Google Scholar
Polyanin, A. D. and Zaitsev, V. F. (2018). Handbook of Ordinary Differential Equations. Exact Solutions, Methods, and Problems. CRC Press, Boca Raton, FL.Google Scholar
Rishel, R. (1991). Controlled wear processes: Modeling optimal control. IEEE Trans. Automatic Control 36, 1100–1102.CrossRefGoogle Scholar
Ye, Z.-S., Wang, Y., Tsui, K.-L. and Pecht, M. (2013). Degradation data analysis using Wiener processes with measurement errors. IEEE Trans. Reliab. 62, 772–780.CrossRefGoogle Scholar