Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gottlieb, Gary
1985.
An optimal betting strategy for repeated games.
Journal of Applied Probability,
Vol. 22,
Issue. 04,
p.
787.
MacLean, L.C.
and
Ziemba, W.T.
1986.
Stochastic Programming.
Vol. 76,
Issue. ,
p.
78.
Gottlieb, Gary
1987.
Non-random shuffling for multiple decks.
Journal of Applied Probability,
Vol. 24,
Issue. 02,
p.
402.
MacLean, L. C.
and
Ziemba, W. T.
1991.
Growth-security profiles in capital accumulation under risk.
Annals of Operations Research,
Vol. 31,
Issue. 1,
p.
501.
Hakansson, Nils H.
and
Ziemba, William T.
1995.
Finance.
Vol. 9,
Issue. ,
p.
65.
Browne, Sid
and
Whitt, Ward
1996.
Portfolio choice and the Bayesian Kelly criterion.
Advances in Applied Probability,
Vol. 28,
Issue. 4,
p.
1145.
Browne, Sid
1998.
The return on investment from proportional portfolio strategies.
Advances in Applied Probability,
Vol. 30,
Issue. 1,
p.
216.
Conway, Daniel G.
and
Koehler, Gary J.
2000.
Interface agents: caveat mercator in electronic commerce.
Decision Support Systems,
Vol. 27,
Issue. 4,
p.
355.
Bruss, F. Thomas
and
Ferguson, Thomas S.
2002.
High-risk and competitive investment models.
The Annals of Applied Probability,
Vol. 12,
Issue. 4,
MacLean, Leonard C.
Sanegre, Rafael
Zhao, Yonggan
and
Ziemba, William T.
2004.
Capital growth with security.
Journal of Economic Dynamics and Control,
Vol. 28,
Issue. 5,
p.
937.
MacLean, Leonard C.
and
Ziemba, William T.
2006.
Theory and Methodology.
Vol. 1,
Issue. ,
p.
429.
Haigh, John
and
Williams, Leighton Vaughan
2008.
Handbook of Sports and Lottery Markets.
p.
357.
Maclean, Leonard C.
and
Ziemba, William T.
2008.
Handbook of Asset and Liability Management.
p.
429.
Hartvigsen, David
2009.
The Action Gambler and Equal-Sized Wagering.
Journal of Applied Probability,
Vol. 46,
Issue. 01,
p.
35.
Li, Ping
2009.
Risk evasion and decision-making in dynamic investments.
p.
1566.
MacLean, Leonard C.
Zhao, Yonggan
and
Ziemba, William T.
2010.
Stochastic Programming.
Vol. 150,
Issue. ,
p.
277.
Maclean, Leonard C.
Thorp, Edward O.
and
Ziemba, William T.
2010.
Long-term capital growth: the good and bad properties of the Kelly and fractional Kelly capital growth criteria.
Quantitative Finance,
Vol. 10,
Issue. 7,
p.
681.
MacLean, Leonard C.
and
Ziemba, William T.
2010.
Encyclopedia of Quantitative Finance.
Epstein, Richard A.
2010.
The Theory of Gambling and Statistical Logic.
p.
43.
Haugh, Martin B.
2011.
A note on constant proportion trading strategies.
Operations Research Letters,
Vol. 39,
Issue. 3,
p.
172.
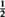 as your advantage tends to 0. The case of non-optimal proportional betting is also treated.
as your advantage tends to 0. The case of non-optimal proportional betting is also treated.



