Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-03T21:32:14.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Ageostrophic instability in rotating shallow water

Published online by Cambridge University Press:  28 September 2012

Peng Wang ,
James C. McWilliams  and
Ziv Kizner
Peng Wang*
Affiliation:
Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, CA 90095-1565, USA
James C. McWilliams
Affiliation:
Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, CA 90095-1565, USA
Ziv Kizner
Affiliation:
Departments of Physics and Mathematics, Bar-Ilan University, Ramat-Gan 52900, Israel
*
†Email address for correspondence: pengwang@atmos.ucla.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Linear instabilities, both momentum-balanced and unbalanced, in several different 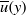$ \overline{u} (y)$ shear profiles are investigated in the rotating shallow water equations. The unbalanced instabilities are strongly ageostrophic and involve inertia–gravity wave motions, occurring only for finite Rossby (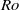$\mathit{Ro}$) and Froude (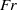$\mathit{Fr}$) numbers. They serve as a possible route for the breakdown of balance in a rotating shallow water system, which leads the energy to cascade towards small scales. Unlike previous work, this paper focuses on general shear flows with non-uniform potential vorticity, and without side or equatorial boundaries or vanishing layer depth (frontal outcropping). As well as classical shear instability among balanced shear wave modes (i.e. B–B type), two types of ageostrophic instability (B–G and G–G) are found. The B–G instability has attributes of both a balanced shear wave mode and an inertia–gravity wave mode. The G–G instability occurs as a sharp resonance between two inertia–gravity wave modes. The criterion for the occurrence of the ageostrophic instability is associated with the second stability condition of Ripa (1983), which requires a sufficiently large local Froude number. When 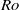$\mathit{Ro}$ and especially 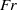$\mathit{Fr}$ increase, the balanced instability is suppressed, while the ageostrophic instabilities are enhanced. The profile of the mean flow also affects the strength of the balanced and ageostrophic instabilities.

JFM classification

Instability: Instability Wakes/Jets: Jets Geophysical and Geological Flows: Shallow water flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 712 , 10 December 2012 , pp. 327 - 353
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balmforth, N. J. 1999 Shear instability in shallow water. J. Fluid Mech. 387, 97–127.Google Scholar
Boss, E., Paldor, N. & Thompson, L. 1996 Stability of a potential vorticity front: from quasi-geostrophy to shallow water. J. Fluid Mech. 315, 65–84.Google Scholar
Bouchut, F., Ribstein, B. & Zeitlin, V. 2011 Inertial, barotropic, and baroclinic instabilities of the Bickley jet in two-layer rotating shallow water model. Phys. Fluids 23, 126601.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Cambridge University Press.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dritschel, D. G. & Vanneste, J. 2006 Instability of a shallow-water potential-vorticity front. J. Fluid Mech. 561, 237–254.Google Scholar
Griffiths, R. W., Killworth, P. D. & Stern, M. E. 1982 Ageostrophic instability of ocean currents. J. Fluid Mech. 117, 343–377.CrossRefGoogle Scholar
Gula, J., Plougonven, R. & Zeitlin, V. 2009 Ageostrophic instabilities of fronts in a channel in a stratified rotating fluid. J. Fluid Mech. 627, 485.Google Scholar
Gula, J. & Zeitlin, V. 2010 Instabilities of buoyancy-driven coastal currents and their nonlinear evolution in the two-layer rotating shallow water model. Part 1. Passive lower layer. J. Fluid Mech. 659, 69–93.Google Scholar
Gula, J., Zeitlin, V. & Bouchut, F. 2010 Instabilities of buoyancy-driven coastal currents and their nonlinear evolution in the two-layer rotating shallow water model. Part 2. Active lower layer. J. Fluid Mech. 665, 209–237.Google Scholar
Hayashi, Y. Y. & Young, W. R. 1987 Stable and unstable shear modes of rotating parallel flows in shallow waters. J. Fluid Mech. 184, 477–504.Google Scholar
Held, I. M. 1985 Pseudomomentum and the orthogonality of modes in shear flows. J. Atmos. Sci. 42, 2280–2288.Google Scholar
Killworth, P., Paldor, N. & Stern, M. 1984 Wave propagation and growth on a surface front in a two-layer geostrophic current. J. Mar. Res. 42, 761–785.Google Scholar
Kizner, Z., Reznik, G., Fridman, B., Khvoles, R. & McWilliams, J. 2008 Shallow-water modons on the $f$ -plane. J. Fluid Mech. 603, 305–329.Google Scholar
Kubokawa, A. 1985 Instability of a geostrophic front and its energetics. Geophys. Astrophys. Fluid 33, 323–357.Google Scholar
Kubokawa, A. 1986 Instability caused by the coalescence of two modes of a one-layer coastal current with a surface front. J. Oceanogr. 42, 373–380.Google Scholar
Lahaye, N. & Zeitlin, V. 2012 Shock modon: a new type of coherent structure in rotating shallow water. Phys. Rev. Lett. 108 (4), 044502.Google Scholar
Lambaerts, J., Lapeyre, G. & Zeitlin, V. 2011 Moist versus dry barotropic instability in a shallow-water model of the atmosphere with moist convection. J. Atmos. Sci. 68, 1234–1252.Google Scholar
Lin, C. C. 1961 Some mathematical problems in the theory of the stability of parallel flows. J. Fluid Mech. 10, 430–438.Google Scholar
McWilliams, J. 1981 Numerical studies of barotropic modons. Dyn. Atmos. Oceans 5, 219–238.Google Scholar
McWilliams, J. C. 2003 Diagnostic force balance and its limits. Nonlinear Process. Geophys. Fluid Dyn. 287–304.Google Scholar
McWilliams, J. C. & Molemaker, M. J. 2004 Ageostrophic, anticyclonic instability of a geostrophic, barotropic boundary current. Phys. Fluids 16, 3720–3725.Google Scholar
McWilliams, J. C. & Yavneh, I. 1998 Fluctuation growth and instability associated with a singularity of the balance equations. Phys. Fluids 10, 2587–2596.Google Scholar
McWilliams, J. C., Yavneh, I., Cullen, M. J. P. & Gent, P. R. 1998 The breakdown of large-scale flows in rotating, stratified fluids. Phys. Fluids 10, 3178–3184.Google Scholar
Ménesguen, C., McWilliams, J. C. & Molemaker, M. J. 2012 Ageostrophic instability in a rotating stratified interior jet. J. Fluid Mech. 711, 599–619.CrossRefGoogle Scholar
Molemaker, M. J. & McWilliams, J. C. 2005 Baroclinic instability and loss of balance. J. Phys. Oceanogr. 35, 1505–1517.Google Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2001 Instability and equilibration of centrifugally stable stratified Taylor–Couette flow. Phys. Rev. Lett. 86, 5270–5273.Google Scholar
Ooyama, K. 1966 On the stability of the baroclinic circular vortex: a sufficient condition for instability. J. Atmos. Sci. 23, 43–53.Google Scholar
Paldor, N. 1983 Linear stability and stable modes of geostrophic fronts. Geophys. Astrophys. Fluid 24, 299–326.Google Scholar
Perret, G., Dubos, T. & Stegner, A. 2011 How large-scale and cyclogeostrophic barotropic instabilities favor the formation of anticyclonic vortices in the ocean. J. Phys. Oceanogr. 41, 303–328.Google Scholar
Poulin, F. J. & Flierl, G. R. 2003 The nonlinear evolution of barotropically unstable jets. J. Phys. Oceanogr. 33, 2173–2192.2.0.CO;2>CrossRefGoogle Scholar
Rayleigh, Lord 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–70.Google Scholar
Ribstein, B., Gula, J. & Zeitlin, V. 2010 (A)geostrophic adjustment of dipolar perturbations, formation of coherent structures and their properties, as follows from high-resolution numerical simulations with rotating shallow water model. Phys. Fluids 22, 116603.Google Scholar
Ripa, P. 1983 General stability conditions for zonal flows in a one-layer model on the beta-plane or the sphere. J. Fluid Mech. 126, 463–489.Google Scholar
Sakai, S. 1989 Rossby–Kelvin instability: a new type of ageostrophic instability caused by a resonance between Rossby waves and gravity waves. J. Fluid Mech. 202, 149–176.Google Scholar
Satomura, T. 1980 An investigation of shear instability in a shallow water. J. Met. Soc. Japan 59, 148.Google Scholar
Yavneh, I., McWilliams, J. C. & Molemaker, M. J. 2001 Non-axisymmetric instability of centrifugally stable stratified Taylor–Couette flow. J. Fluid Mech. 448, 1–21.Google Scholar