1. Introduction
The turbulence cascade is a scientific paradigm that dates back to the beginning of the 20th century. It has been addressed in different ways, and the objects used to describe it are many. From the classical view of Richardson (Reference Richardson1922) to the recent analysis of coherent structures (Cardesa, Vela-Martín & Jiménez Reference Cardesa, Vela-Martín and Jiménez2017), through the statistical theory of Kolmogorov (Reference Kolmogorov1941) or the spectral representation (Waleffe Reference Waleffe1992), all descriptions focus on the same phenomena through diverse approaches. In all cases, the cascade tries to account for the gap between the scales where energy is produced and those at which it is dissipated. A concept of energy flux or energy transport from large to small scales is always present. We know that this cascade must take place because this gap must be bridged, but the mechanisms that underlie it are to date poorly or ambiguously identified. A thorough description of these mechanisms and their causes is needed if a complete theory of turbulence is to be constructed, and necessarily involves exploring multiple representations of the turbulence cascade.
In this paper we expand the investigation of the energy cascade from the perspective of dynamical system theory and statistical mechanics. We explore microscopical reversibility in the inertial range dynamics, and its implications for the representation of the turbulence cascade as a process driven by entropy production (Kraichnan Reference Kraichnan1967), emphasising that the prevalence of a direct energy transfer is probabilistic, rather than an unavoidable consequence of the equations of motion.
Turbulence is a highly dissipative and essentially irreversible phenomenon. An intrinsic source of the irreversibility of the Navier–Stokes equations is viscosity, which accounts for the molecular diffusion of momentum. However, when the Reynolds number is high, only the smallest scales with locally low Reynolds numbers are affected. At scales much larger than the Kolmogorov length, viscous effects are negligible and dynamics is only driven by inertial forces, which, as we will demonstrate, generate time-reversible dynamics. This is clear from the truncated Euler equations, which are known to be reversible and to display features specific to fully developed turbulent flows under certain conditions (She & Jackson Reference She and Jackson1993; Cichowlas et al. Reference Cichowlas, Bonaïti, Debbasch and Brachet2005). Although these equations are invariant to a reversal of the time axis, statistical irreversibility appears as a tendency towards preferred evolutions when the flow is driven out of equilibrium. The energy cascade is an important manifestation of this irreversibility. Thus, we should distinguish between intrinsic irreversibility, which is directly imposed by the equations of motion, and statistical irreversibility, which is a consequence of the dynamical complexity of highly chaotic systems with many degrees of freedom. In the absence of an intrinsic irreversible mechanism, a dynamical system can be microscopically reversible and statistically, or macroscopically, irreversible. This idea, which is widely understood in the study of dynamical systems, has not been sufficiently investigated in the context of the turbulence cascade.
The concept of microscopically reversible turbulence has been treated in the literature. Gallavotti (Reference Gallavotti1997) proposed a reversible formulation of dissipation in an attempt to apply the theory of hyperbolic dynamical systems to turbulence, and to study fluctuations out of equilibrium. This idea was later applied by Biferale, Pierotti & Vulpiani (Reference Biferale, Pierotti and Vulpiani1998) to study a reversible shell model of the turbulence cascade under weak departures from equilibrium. Rondoni & Segre (Reference Rondoni and Segre1999) and Gallavotti, Rondoni & Segre (Reference Gallavotti, Rondoni and Segre2004) further extended reversible models to two-dimensional turbulence, proving that reversible dissipative systems can properly represent some aspects of turbulence dynamics. Reversibility is also a property of some common large-eddy simulation models, which reproduce the odd symmetry of the energy fluxes on the velocities and yield fully reversible representations of the sub-grid stresses (Bardina, Ferziger & Reynolds Reference Bardina, Ferziger and Reynolds1980; Germano et al. Reference Germano, Piomelli, Moin and Cabot1991; Winckelmans et al. Reference Winckelmans, Wray, Vasilyev and Jeanmart2001). Despite the statistical irreversibility of the energy cascade, previous investigations have also shown that it is possible to reverse turbulence in time. Carati, Winckelmans & Jeanmart (Reference Carati, Winckelmans and Jeanmart2001) constructed a reversible system using a standard dynamic Smagorinsky model from which molecular dissipation has been removed. When reversed in time after decaying for a while, this system recovers all its lost energy and other turbulent quantities; during the inverse evolution, the system develops a sustained inverse energy cascade towards the large scales. This numerical experiment shows that, even if we empirically know that spontaneously observing an extended inverse cascade is extremely unlikely, such cascades are possible, thus exposing their probabilistic nature. We exploit here the experimental system in Carati et al. (Reference Carati, Winckelmans and Jeanmart2001) as a tool to explore the statistical irreversibility of the energy cascade.
As originally argued by Loschmidt (Reference Loschmidt1876), the analysis of the equations of motion of any reversible dynamical system reveals that for each direct evolution there exists a dual inverse evolution, leading to the paradox of how macroscopically irreversible dynamics stem from microscopically reversible dynamics. This apparent inconsistency is bridged with the concepts of entropy and entropy production, which account for the disparate probabilities of direct and inverse evolutions. The concept of entropy is supported on the description of physical systems by time-invariant probability distributions in a highly dimensional phase space. While this approach has been successfully applied to describe equilibrium systems, its application to out-of-equilibrium systems is still incomplete.
In the case of turbulence, the application of entropy to justify the direction of the cascade dates back several decades. Kraichnan (Reference Kraichnan1967) used absolute equilibrium ensembles of the inviscid Navier–Stokes equations to predict the inverse cascade of energy in two-dimensional turbulence. These equilibrium ensembles are derived from the equipartition distribution, which maximises a Gibbs entropy, implicitly suggesting a quantitative connection between entropy and energy fluxes. Although this approach has proved successful to predict or justify the direction of fluxes in diverse out-of-equilibrium turbulent systems, including magnetohydrodynamic turbulence (Frisch et al. Reference Frisch, Pouquet, Léorat and Mazure1975) and incompressible three-dimensional turbulence (Orszag Reference Orszag1974), it fails to offer useful information on the mechanisms that cause the prevalence of a particular direction of the fluxes. For that purpose, rather than time-invariant equilibrium distributions, we must consider the dynamical information encoded in the temporal evolution of out-of-equilibrium probability distributions towards absolute equilibrium. Unfortunately, turbulence exhibits a wide range of spatial and temporal scales, which renders its description in a highly dimensional phase space all but intractable.
The main contribution of this work is to bridge the gap between the evolution of probability distributions in phase space, and the physical structure of turbulent flows. We characterise the energy cascade as a local process in physical space, which can be robustly quantified independently of the definition of energy fluxes. These results extend previous works on the locality of the energy cascade (Meneveau & Lund Reference Meneveau and Lund1994; Eyink Reference Eyink2005; Domaradzki & Carati Reference Domaradzki and Carati2007; Eyink & Aluie Reference Eyink and Aluie2009; Cardesa et al. Reference Cardesa, Vela-Martín, Dong and Jiménez2015, Reference Cardesa, Vela-Martín and Jiménez2017; Doan et al. Reference Doan, Swaminathan, Davidson and Tanahashi2018). We consider the statistics of local energy transfer events to study the probability of inverse cascades over restricted domains, connecting statistical irreversibility, a property of phase-space ensembles related to entropy production, with the local dynamics of turbulence in physical space.
The probabilistic nature of the cascade requires that we characterise its mechanism also from a probabilistic perspective. A meaningful description of the energy cascade must first identify the dynamically relevant mechanisms related to energy transfer, and subsequently establish the causes of the prevalence of the direct mechanisms over the inverse ones. We address both by analysing the filtered velocity gradient tensor through its invariants (Naso & Pumir Reference Naso and Pumir2005; Lozano-Durán, Holzner & Jiménez Reference Lozano-Durán, Holzner and Jiménez2016; Danish & Meneveau Reference Danish and Meneveau2018), and by determining their relation to the local energy fluxes in physical space. These invariants describe the local geometry of turbulent flows, and offer a compact representation of the structure and dynamics of the velocity gradients. We will show that the structure of the direct cascade differs substantially from that of the inverse cascade, and that differences are most significant in regions where the dynamics of the rate-of-strain tensor dominates over the vorticity vector. Moreover, we show that strain-dominated regions are responsible for most of the local energy fluxes, evidencing the relevant role of the rate-of-strain tensor in the energy cascade and in the statistical irreversibility of turbulent flows.
Following these results we propose a probabilistic argument to explain the prevalence of direct energy transfer by taking into consideration the interaction of the rate-of-strain tensor with the non-local component of the pressure Hessian. In this frame, we justify the higher probability of direct over inverse cascades by noting that the latter require the organisation of a large number of spatial degrees of freedom, whereas the direct cascade results from space-local dynamics.
This paper is organised as follows. In § 2 we review the origin of statistical irreversibility in the turbulence cascade as explained by the evolution of out-of-equilibrium ensembles and the production of information entropy. In § 3 we present the reversible sub-grid model and the experimental set-up for the reversible turbulent system that constitutes the foundations of this investigation. In order to examine the entropic (probabilistic) nature of the turbulence cascade, we conduct different numerical experiments on this system, which are detailed in § 4. In § 5 we characterise the distribution of inverse trajectories in phase space and the structure of the energy cascade in physical space. In § 6 we compare the structure and dynamics of the direct and inverse evolutions through the invariants of the velocity gradient tensor and their relation to the local energy fluxes. Finally, conclusions are offered in § 7.
2. Entropy production and the turbulence cascade
We explore in this section the origin of irreversibility in the inertial energy cascade from the perspective of statistical mechanics. We use the concept of entropy and entropy production to justify the prevalence of direct energy cascades, and suggest a connection between these quantities and the interscale energy fluxes. Previous papers in this direction are Orszag (Reference Orszag1974) and Holloway (Reference Holloway1986).
Let us consider an ![]() $n$-dimensional state vector in phase space,
$n$-dimensional state vector in phase space, ![]() $\boldsymbol {\chi }=(\chi _1,\chi _2,\ldots ,\chi _n)$, representing the
$\boldsymbol {\chi }=(\chi _1,\chi _2,\ldots ,\chi _n)$, representing the ![]() $n$ degrees of freedom of a deterministic dynamical system, and its probability density,
$n$ degrees of freedom of a deterministic dynamical system, and its probability density, ![]() $P(\boldsymbol {\chi })$. Assuming that this representation of the system satisfies the Liouville theorem, i.e. that the dynamics preserve phase-space volume and, therefore, probability density along trajectories, we partition the accessible phase space in
$P(\boldsymbol {\chi })$. Assuming that this representation of the system satisfies the Liouville theorem, i.e. that the dynamics preserve phase-space volume and, therefore, probability density along trajectories, we partition the accessible phase space in ![]() $\gamma =1, 2,\dots , m$ coarse-grained subsets of volume
$\gamma =1, 2,\dots , m$ coarse-grained subsets of volume ![]() $\omega _\gamma$. The probability of finding a state in
$\omega _\gamma$. The probability of finding a state in ![]() $\gamma$ is
$\gamma$ is
where the integral is taken over ![]() $\omega _\gamma$. We define a Gibbs coarse-grained entropy,
$\omega _\gamma$. We define a Gibbs coarse-grained entropy,
 \begin{equation} H={-}\sum_{\gamma} {P_\gamma}\log\left(P_\gamma\frac{\varUpsilon}{\omega_\gamma}\right), \end{equation}
\begin{equation} H={-}\sum_{\gamma} {P_\gamma}\log\left(P_\gamma\frac{\varUpsilon}{\omega_\gamma}\right), \end{equation}
where ![]() $\varUpsilon =\sum _{\gamma }\omega _\gamma$, and the summation is done over all the sub-volumes of the partition. This entropy is maximised for the coarse-grained probability distribution
$\varUpsilon =\sum _{\gamma }\omega _\gamma$, and the summation is done over all the sub-volumes of the partition. This entropy is maximised for the coarse-grained probability distribution ![]() $P_\gamma /\omega _\gamma =\text {const}$, although the value of this maximum depends on the geometrical properties of the partition, such as the volume of the subsets, and can only be defined up to a constant. This definition of entropy can also be connected with information theory, such that the information on an ensemble of realisations is proportional to minus its entropy (Latora & Baranger Reference Latora and Baranger1999).
$P_\gamma /\omega _\gamma =\text {const}$, although the value of this maximum depends on the geometrical properties of the partition, such as the volume of the subsets, and can only be defined up to a constant. This definition of entropy can also be connected with information theory, such that the information on an ensemble of realisations is proportional to minus its entropy (Latora & Baranger Reference Latora and Baranger1999).
Let us consider the Euler equations projected on a truncated Fourier basis, ![]() $k\leqslant k_{max}$, where
$k\leqslant k_{max}$, where ![]() $k$ is the wavenumber magnitude. This system conserves energy and satisfies Liouville's equation for the Fourier coefficients of the fluid velocity (Orszag Reference Orszag1974; Kraichnan Reference Kraichnan1975). If we choose an ensemble of states far from equilibrium, such as a set of velocity fields with a given total kinetic energy and an energy spectrum proportional to
$k$ is the wavenumber magnitude. This system conserves energy and satisfies Liouville's equation for the Fourier coefficients of the fluid velocity (Orszag Reference Orszag1974; Kraichnan Reference Kraichnan1975). If we choose an ensemble of states far from equilibrium, such as a set of velocity fields with a given total kinetic energy and an energy spectrum proportional to ![]() $k^{-5/3}$ (Kolmogorov Reference Kolmogorov1941),
$k^{-5/3}$ (Kolmogorov Reference Kolmogorov1941), ![]() $H$ is initially low because the states are localised in a special subset of phase space. As the ensemble evolves, the probability density is conserved along each trajectory,
$H$ is initially low because the states are localised in a special subset of phase space. As the ensemble evolves, the probability density is conserved along each trajectory, ![]() $P(\boldsymbol {\chi }(t))=\text {const}$, and the chaotic interaction of a large number of degrees of freedom leads to the phase-space ‘mixing’ of the probability density, resulting in the homogenisation of the coarse-grained probabilities,
$P(\boldsymbol {\chi }(t))=\text {const}$, and the chaotic interaction of a large number of degrees of freedom leads to the phase-space ‘mixing’ of the probability density, resulting in the homogenisation of the coarse-grained probabilities, ![]() $P_\gamma$. As a consequence,
$P_\gamma$. As a consequence, ![]() $H$ increases until the coarse-grained probability over each element of the partition reaches
$H$ increases until the coarse-grained probability over each element of the partition reaches ![]() $P_\gamma /\omega _\gamma =\text {const}$, which maximises (2.2) and corresponds to absolute equilibrium. The evolution of
$P_\gamma /\omega _\gamma =\text {const}$, which maximises (2.2) and corresponds to absolute equilibrium. The evolution of ![]() $H$ towards a maximum manifests the second law of thermodynamics, and explains the emergence of statistical irreversibility in microscopically reversible systems out of equilibrium.
$H$ towards a maximum manifests the second law of thermodynamics, and explains the emergence of statistical irreversibility in microscopically reversible systems out of equilibrium.
In the phase-space representation in terms of the Fourier coefficients, mixing is implemented by the conservative exchange of energy among triads of Fourier modes, which distributes energy evenly across all modes (Kraichnan Reference Kraichnan1959), so that the equilibrium energy spectrum is proportional to the number of modes in each wavenumber shell, ![]() $4{\rm \pi} k^2$. This is the spectrum of the most probable macroscopic state, i.e. the spectrum that represents the largest number of microscopic realisations. States in the equilibrium ensemble have more energy in the small scales than the states in our initial out-of-equilibrium ensemble, implying that the evolution towards equilibrium and the increase of entropy corresponds, on average, to energy flux towards the small scales. However, note that the scale is not a property of the phase space itself, nor of the entropy. In our example, the scale has been overlaid on the system by labelling the Fourier coefficients by their wavenumbers, where a greater number of coefficients are tagged as ‘small scale’ than as ‘large scale’. Moreover, the evolution towards equilibrium is true only in a statistical sense. Since there is no deterministic ‘force’ driving the system to equilibrium, it is possible to find trajectories in the ensemble for which energy sloshes back and forth among different scales. One cascade direction is simply more probable than the other.
$4{\rm \pi} k^2$. This is the spectrum of the most probable macroscopic state, i.e. the spectrum that represents the largest number of microscopic realisations. States in the equilibrium ensemble have more energy in the small scales than the states in our initial out-of-equilibrium ensemble, implying that the evolution towards equilibrium and the increase of entropy corresponds, on average, to energy flux towards the small scales. However, note that the scale is not a property of the phase space itself, nor of the entropy. In our example, the scale has been overlaid on the system by labelling the Fourier coefficients by their wavenumbers, where a greater number of coefficients are tagged as ‘small scale’ than as ‘large scale’. Moreover, the evolution towards equilibrium is true only in a statistical sense. Since there is no deterministic ‘force’ driving the system to equilibrium, it is possible to find trajectories in the ensemble for which energy sloshes back and forth among different scales. One cascade direction is simply more probable than the other.
In the previous discussion we have disregarded the dynamics of the flow, whose evolution has been reduced to the chaotic mixing in phase space. In reality, the system is restricted by the equations of motion, and not all evolutions are possible. At the very least, the system only evolves on the hypersurfaces defined by its invariants, which thus determine different equilibrium spectra. The most obvious invariant of the inviscid Euler equations is the total energy, which can be written as ![]() $\mathcal {E}=\sum _k \chi _k^2$. But, because this formula does not explicitly involve the scale, the restriction to an energy shell does not modify energy equipartition, nor the
$\mathcal {E}=\sum _k \chi _k^2$. But, because this formula does not explicitly involve the scale, the restriction to an energy shell does not modify energy equipartition, nor the ![]() $k^2$ spectrum. When there is more than one invariant, the accessible phase space is the intersection of their corresponding isosurfaces, which generically depends on the relative magnitude of the total conserved quantities. This is the case of the two-dimensional inviscid Euler equations, which also conserve the enstrophy (Kraichnan & Montgomery Reference Kraichnan and Montgomery1980), or the inviscid and infinitely conducting magnetohydrodynamic equations, which also conserve the magnetic helicity (Frisch et al. Reference Frisch, Pouquet, Léorat and Mazure1975).
$k^2$ spectrum. When there is more than one invariant, the accessible phase space is the intersection of their corresponding isosurfaces, which generically depends on the relative magnitude of the total conserved quantities. This is the case of the two-dimensional inviscid Euler equations, which also conserve the enstrophy (Kraichnan & Montgomery Reference Kraichnan and Montgomery1980), or the inviscid and infinitely conducting magnetohydrodynamic equations, which also conserve the magnetic helicity (Frisch et al. Reference Frisch, Pouquet, Léorat and Mazure1975).
Unfortunately, although the form of the equilibrium spectrum suggests where the system ‘would like to go’, it does not by itself determine the direction of the cascades in out-of-equilibrium steady states. These states can be established by imposing boundary conditions in phase space, such as forcing the large scales, and adding dissipation at the small ones, resulting in a steady flux of energy from one boundary to the other. The intuition is that the cascade develops as the energy moves among scales, trying to establish the equilibrium spectrum, but this final state is never achieved because the boundary conditions sustain the energy flux and maintain the system out of equilibrium.
In summary, statistical irreversibility and the direct energy cascade arise in out-of-equilibrium ensembles of the truncated Euler equations as consequences of three aspects of inertial dynamics: the first one is the conservation of phase-space probabilities along trajectories, due to Liouville; the second one is the strongly mixing nature of turbulent dynamics in the inertial range; and the third one is that small scales are represented by a much higher number of degrees of freedom than larger ones. These properties intuitively answer the central question of why direct cascades are more probable than inverse ones. Although possible, the latter are inconsistent with the tendency of turbulent flows to evolve towards equilibrium, because they take energy from the more numerous small eddies and ‘organise’ it into less common larger ones.
However, these general statistical concepts say little about the dynamics of the cascade. The main contribution of our work is to explain the origin of statistical irreversibility by considering the structure of the energy cascade in physical space, connecting the description of turbulence as a dynamical system evolving in a highly dimensional phase space to the space-local physical structure of isotropic turbulence. We do so by describing the physical mechanisms that locally determine the prevalence of the direct over the inverse energy cascade.
3. The reversible sub-grid model
A popular technique to alleviate the huge computational cost of simulating industrial turbulent flows is large-eddy simulation, which filters out the flow scales below a prescribed cutoff length, and only retains the dynamics of the larger eddies. We use it here to generate microscopically reversible turbulence. The equations governing the large scales are obtained by filtering the incompressible Navier–Stokes equations,
 \begin{equation} \left.\begin{aligned} &\partial_t \bar{u}_i+\bar{u}_j\partial_j \bar{u}_i={-}\partial_i \bar p +\partial_j \tau_{ij},\\ &\partial_i \bar{u}_i=0, \end{aligned}\right\}\end{equation}
\begin{equation} \left.\begin{aligned} &\partial_t \bar{u}_i+\bar{u}_j\partial_j \bar{u}_i={-}\partial_i \bar p +\partial_j \tau_{ij},\\ &\partial_i \bar{u}_i=0, \end{aligned}\right\}\end{equation}
where the overline ![]() $(\bar {\cdot })$ represents filtering at the cutoff length
$(\bar {\cdot })$ represents filtering at the cutoff length ![]() $\bar {\varDelta }$,
$\bar {\varDelta }$, ![]() $u_i$ is the
$u_i$ is the ![]() $i$-th component of the velocity vector
$i$-th component of the velocity vector ![]() $\boldsymbol {u}=(u_i)$, with
$\boldsymbol {u}=(u_i)$, with ![]() $i=1,\ldots ,3$,
$i=1,\ldots ,3$, ![]() $\partial _i$ is the partial derivative with respect to the
$\partial _i$ is the partial derivative with respect to the ![]() $i$-th direction,
$i$-th direction, ![]() $p$ is a modified pressure and repeated indices imply summation. We assume that the cutoff length is much larger than the viscous scale, and neglect in (3.1) the effect of viscosity on the resolved scales. The interaction of the scales below the cutoff filter with the resolved ones is represented by the sub-grid stress (SGS) tensor,
$p$ is a modified pressure and repeated indices imply summation. We assume that the cutoff length is much larger than the viscous scale, and neglect in (3.1) the effect of viscosity on the resolved scales. The interaction of the scales below the cutoff filter with the resolved ones is represented by the sub-grid stress (SGS) tensor, ![]() $\tau _{ij}=\bar {u}_i \bar {u}_j-\overline {u_iu_j}$, which is unknown and must be modelled.
$\tau _{ij}=\bar {u}_i \bar {u}_j-\overline {u_iu_j}$, which is unknown and must be modelled.
One of the consequences of this interaction is an energy flux towards or from the unresolved scales, which derives from triple products of the velocity field and its derivatives, and is implicitly time reversible. However, this flux is often modelled as a dissipative energy sink, destroying time reversibility and the possibility of inverse energy fluxes (backscatter). In an attempt to yield a more realistic representation of the dynamics of the energy cascade, some SGS models try to reproduce backscatter, which also restores the time reversibility of energy fluxes. This is the case for the family of dynamic models, which are designed to adapt the effect of the unresolved scales to the state of the resolved flow, eliminating tuning parameters. A widely used reversible model is the dynamic Smagorinsky model of Germano et al. (Reference Germano, Piomelli, Moin and Cabot1991), based upon the assumption that the cutoff filter lies within the self-similar inertial range of scales, and that the sub-grid stresses at the filter scale can be matched locally to those at a coarser test filter. This idea is applied to the classical Smagorinsky (Reference Smagorinsky1963) model in which sub-grid stresses are assumed to be parallel to the rate-of-strain tensor of the resolved scales, ![]() $\bar {S}_{ij}=(\partial _i \bar {u}_j +\partial _j \bar {u}_i)/{2}$, such that
$\bar {S}_{ij}=(\partial _i \bar {u}_j +\partial _j \bar {u}_i)/{2}$, such that ![]() $\tau _{ij}^T=2 \nu _s \bar {S}_{ij}$, where
$\tau _{ij}^T=2 \nu _s \bar {S}_{ij}$, where ![]() $\nu _s$ is referred to as the eddy viscosity and the ‘
$\nu _s$ is referred to as the eddy viscosity and the ‘![]() $T$’ superscript refers to the traceless part of the tensor. Introducing
$T$’ superscript refers to the traceless part of the tensor. Introducing ![]() $\bar {\varDelta }$ and
$\bar {\varDelta }$ and ![]() $|\bar {S}|$ as characteristic length and time scales, respectively, and a dimensionless scalar parameter
$|\bar {S}|$ as characteristic length and time scales, respectively, and a dimensionless scalar parameter ![]() $C$, the model is
$C$, the model is
where ![]() $\nu _s=C \bar { \varDelta }^2 |\bar {S}|$ and
$\nu _s=C \bar { \varDelta }^2 |\bar {S}|$ and ![]() $|S|=\sqrt {2 S_{lm}S_{lm}}$. Filtering (3.1) with a test filter of width
$|S|=\sqrt {2 S_{lm}S_{lm}}$. Filtering (3.1) with a test filter of width ![]() $\tilde {\varDelta }=2\bar {\varDelta }$, denoted by
$\tilde {\varDelta }=2\bar {\varDelta }$, denoted by ![]() $(\tilde \cdot )$, we obtain expressions for the sub-grid stresses at both scales, which are matched to obtain an equation for
$(\tilde \cdot )$, we obtain expressions for the sub-grid stresses at both scales, which are matched to obtain an equation for ![]() $C$,
$C$,
where ![]() $\mathcal {M}_{ij}= {\tilde {\varDelta }}^2 |\tilde {\bar {S}}| \tilde {\bar {S}}_{ij}- {\bar {\varDelta }}^2\widetilde {|\bar {S}|\bar {S}_{ij}}$ and
$\mathcal {M}_{ij}= {\tilde {\varDelta }}^2 |\tilde {\bar {S}}| \tilde {\bar {S}}_{ij}- {\bar {\varDelta }}^2\widetilde {|\bar {S}|\bar {S}_{ij}}$ and ![]() $\mathcal {L}_{ij}=(\widetilde {\bar {u}_i\bar {u}_j} - \widetilde {\bar {u}}_i \widetilde {\bar {u}}_j)/{2}$. A spatially local least-square solution,
$\mathcal {L}_{ij}=(\widetilde {\bar {u}_i\bar {u}_j} - \widetilde {\bar {u}}_i \widetilde {\bar {u}}_j)/{2}$. A spatially local least-square solution, ![]() $C_\ell$, is obtained by contracting (3.3) with
$C_\ell$, is obtained by contracting (3.3) with ![]() $\mathcal {M}_{ij}$,
$\mathcal {M}_{ij}$,
This formulation occasionally produces local negative dissipation, ![]() $C_\ell (\boldsymbol {x}, t)<0$, which may lead to undesirable numerical instabilities (Ghosal et al. Reference Ghosal, Lund, Moin and Akselvoll1995; Meneveau, Lund & Cabot Reference Meneveau, Lund and Cabot1996). To avoid this problem, (3.3) is often spatially averaged after contraction to obtain a mean value for the dynamic parameter (Lilly Reference Lilly1992),
$C_\ell (\boldsymbol {x}, t)<0$, which may lead to undesirable numerical instabilities (Ghosal et al. Reference Ghosal, Lund, Moin and Akselvoll1995; Meneveau, Lund & Cabot Reference Meneveau, Lund and Cabot1996). To avoid this problem, (3.3) is often spatially averaged after contraction to obtain a mean value for the dynamic parameter (Lilly Reference Lilly1992),
where ![]() $\langle \cdot \rangle$ denotes spatial averaging over the computational box. Since
$\langle \cdot \rangle$ denotes spatial averaging over the computational box. Since ![]() $\tau _{ij} {\bar {S}}_{ij}= C_s {\bar {\varDelta }}^2 |{\bar {S}}_{ij}|^3$, a positive
$\tau _{ij} {\bar {S}}_{ij}= C_s {\bar {\varDelta }}^2 |{\bar {S}}_{ij}|^3$, a positive ![]() $C_s$ implies that energy flows from the resolved to the unresolved scales, and defines a direct cascade. The sign of
$C_s$ implies that energy flows from the resolved to the unresolved scales, and defines a direct cascade. The sign of ![]() $C_s$ depends on the velocity field through
$C_s$ depends on the velocity field through ![]() $\mathcal {M}_{ij}$, which is odd in the rate-of-strain tensor, so that
$\mathcal {M}_{ij}$, which is odd in the rate-of-strain tensor, so that ![]() $C_s(-\boldsymbol {u})=-C_s(\boldsymbol {u})$. Given a flow field with
$C_s(-\boldsymbol {u})=-C_s(\boldsymbol {u})$. Given a flow field with ![]() $C_s>0$, a change in the sign of the velocities leads to another one with negative eddy viscosity.
$C_s>0$, a change in the sign of the velocities leads to another one with negative eddy viscosity.
This property allows us to construct a reversible turbulent system using the dynamic Smagorinsky model and removing molecular viscosity. The equations for the resolved velocity field, ![]() $\bar {\boldsymbol {u}}$, are
$\bar {\boldsymbol {u}}$, are
 \begin{equation} \left.\begin{aligned} &\partial_t u_i+u_j\partial_j u_i={-}\partial_i p + C_s \bar{\varDelta}^2 \partial_j {|S|} S_{ij},\\ &\partial_i u_i=0, \end{aligned}\right\}\end{equation}
\begin{equation} \left.\begin{aligned} &\partial_t u_i+u_j\partial_j u_i={-}\partial_i p + C_s \bar{\varDelta}^2 \partial_j {|S|} S_{ij},\\ &\partial_i u_i=0, \end{aligned}\right\}\end{equation}
together with (3.5), where the filtering notation has been dropped for conciseness. Equations (3.6) are invariant to the transformation ![]() $t\rightarrow -t$ and
$t\rightarrow -t$ and ![]() $\boldsymbol {u} \rightarrow -\boldsymbol {u}$, and changing the sign of the velocities is equivalent to inverting the time axis (Carati et al. Reference Carati, Winckelmans and Jeanmart2001).
$\boldsymbol {u} \rightarrow -\boldsymbol {u}$, and changing the sign of the velocities is equivalent to inverting the time axis (Carati et al. Reference Carati, Winckelmans and Jeanmart2001).
4. Experiments on turbulence under time reversal
4.1. Numerical set-up
A standard Rogallo (Reference Rogallo1981) code is used to perform a series of experiments on decaying triply periodic homogeneous turbulence in a ![]() $(2{\rm \pi} )^3$ box. Equations (3.6) are solved with the dynamic Smagorinsky model described in the previous section. The three velocity components are projected on a Fourier basis, and the nonlinear terms are calculated using a fully dealiased pseudo-spectral method with a 2/3 truncation rule (Canuto et al. Reference Canuto, Hussaini, Quarteroni and Thomas2012). We denote the wavenumber vector by
$(2{\rm \pi} )^3$ box. Equations (3.6) are solved with the dynamic Smagorinsky model described in the previous section. The three velocity components are projected on a Fourier basis, and the nonlinear terms are calculated using a fully dealiased pseudo-spectral method with a 2/3 truncation rule (Canuto et al. Reference Canuto, Hussaini, Quarteroni and Thomas2012). We denote the wavenumber vector by ![]() $\boldsymbol {k}$, and its magnitude by
$\boldsymbol {k}$, and its magnitude by ![]() $k=|{\boldsymbol {k}}|$. The number of physical points in each direction before dealiasing is
$k=|{\boldsymbol {k}}|$. The number of physical points in each direction before dealiasing is ![]() $N=128$, so that the highest fully resolved wavenumber is
$N=128$, so that the highest fully resolved wavenumber is ![]() $k_{max}=42$. An explicit third-order Runge–Kutta is used for temporal integration, and the time step is adjusted to a constant Courant–Friedrichs–Lewy number equal to
$k_{max}=42$. An explicit third-order Runge–Kutta is used for temporal integration, and the time step is adjusted to a constant Courant–Friedrichs–Lewy number equal to ![]() $0.2$. A Gaussian filter whose Fourier expression is
$0.2$. A Gaussian filter whose Fourier expression is
where ![]() $\varDelta$ is the filter width (Aoyama et al. Reference Aoyama, Ishihara, Kaneda, Yokokawa, Itakura and Uno2005), is used to evaluate
$\varDelta$ is the filter width (Aoyama et al. Reference Aoyama, Ishihara, Kaneda, Yokokawa, Itakura and Uno2005), is used to evaluate ![]() $C_s$ in (3.5). The equations are explicitly filtered at the cutoff filter
$C_s$ in (3.5). The equations are explicitly filtered at the cutoff filter ![]() $\bar {\varDelta }$, and at the test filter
$\bar {\varDelta }$, and at the test filter ![]() $\tilde \varDelta =2\bar {\varDelta }=\varDelta _{g}\sqrt {6}$, where
$\tilde \varDelta =2\bar {\varDelta }=\varDelta _{g}\sqrt {6}$, where ![]() $\varDelta _{g}=2{\rm \pi} /N$ is the grid resolution before dealiasing. Although the explicit cutoff filter is not strictly necessary, it is used for consistency and numerical stability.
$\varDelta _{g}=2{\rm \pi} /N$ is the grid resolution before dealiasing. Although the explicit cutoff filter is not strictly necessary, it is used for consistency and numerical stability.
The energy spectrum is defined as
where ![]() $\hat {u}_i(\boldsymbol {k})$ are the Fourier coefficients of the
$\hat {u}_i(\boldsymbol {k})$ are the Fourier coefficients of the ![]() $i$-th velocity component, the asterisk is complex conjugation and
$i$-th velocity component, the asterisk is complex conjugation and ![]() $\langle \cdot \rangle _k$ denotes averaging over shells of thickness
$\langle \cdot \rangle _k$ denotes averaging over shells of thickness ![]() $k\pm 0.5$. The kinetic energy per unit mass is
$k\pm 0.5$. The kinetic energy per unit mass is ![]() $\mathcal {E}=\langle {u_i u_i}\rangle /{2}=\sum _k E(k,t)$, where
$\mathcal {E}=\langle {u_i u_i}\rangle /{2}=\sum _k E(k,t)$, where ![]() $\sum _k$ denotes summation over all wavenumbers.
$\sum _k$ denotes summation over all wavenumbers.
Meaningful units are required to characterise the simulations. The standard reference for the small scales in Navier–Stokes turbulence are Kolmogorov units, but they are not applicable here because of the absence of molecular viscosity. Instead we derive pseudo-Kolmogorov units using the mean eddy viscosity, ![]() $\langle \nu _s\rangle = C_s\bar {\varDelta }^2 \langle |S| \rangle$, and the mean sub-grid energy transfer at the cutoff scale,
$\langle \nu _s\rangle = C_s\bar {\varDelta }^2 \langle |S| \rangle$, and the mean sub-grid energy transfer at the cutoff scale, ![]() $\langle \epsilon _s\rangle = C_s\bar {\varDelta }^2 \langle |S|^3 \rangle$. The time and length scale derived from these quantities are
$\langle \epsilon _s\rangle = C_s\bar {\varDelta }^2 \langle |S|^3 \rangle$. The time and length scale derived from these quantities are ![]() $\tau _s=(\langle \nu _s\rangle /\langle \epsilon _s \rangle )^{1/2}$ and
$\tau _s=(\langle \nu _s\rangle /\langle \epsilon _s \rangle )^{1/2}$ and ![]() $\eta _s=(\langle \nu \rangle ^3_s/\langle \epsilon _s \rangle )^{1/4}$, respectively. We find these units to be consistent with the physics of turbulence, such that the peak of the enstrophy spectrum,
$\eta _s=(\langle \nu \rangle ^3_s/\langle \epsilon _s \rangle )^{1/4}$, respectively. We find these units to be consistent with the physics of turbulence, such that the peak of the enstrophy spectrum, ![]() $k^2E(k)$, is located at
$k^2E(k)$, is located at ![]() ${\sim }25\eta _s$. In direct numerical simulations, this peak lies at
${\sim }25\eta _s$. In direct numerical simulations, this peak lies at ![]() ${\sim }20\eta$.
${\sim }20\eta$.
The larger eddies are characterised by the integral length, velocity and time scales (Batchelor Reference Batchelor1953), respectively defined as
 \begin{equation} L={\rm \pi} \frac{\displaystyle\sum_k E(k,t)/k}{\displaystyle\sum_k E(k,t)}, \end{equation}
\begin{equation} L={\rm \pi} \frac{\displaystyle\sum_k E(k,t)/k}{\displaystyle\sum_k E(k,t)}, \end{equation}
![]() $u'=\sqrt {2\mathcal {E}/3}$ and
$u'=\sqrt {2\mathcal {E}/3}$ and ![]() $T=L/u'$. The Reynolds number based on the integral scale is defined as
$T=L/u'$. The Reynolds number based on the integral scale is defined as ![]() $Re_L=u' L/\langle \nu _s\rangle$, and the separation of scales in the simulation is represented by the ratio
$Re_L=u' L/\langle \nu _s\rangle$, and the separation of scales in the simulation is represented by the ratio ![]() $L/\eta _s$.
$L/\eta _s$.
In the following we study the energy flux both in Fourier space, averaged over the computational box, and locally in physical space.
The energy flux across the surface of a sphere in Fourier space with wavenumber magnitude ![]() $k$ can be expressed as
$k$ can be expressed as
where ![]() $\mathcal {D}_i=u_j\partial _j u_i$ and a negative
$\mathcal {D}_i=u_j\partial _j u_i$ and a negative ![]() $\varPi$ denotes energy flowing to larger scales.
$\varPi$ denotes energy flowing to larger scales.
We use two different definitions of the local interscale energy flux in physical space,
 \begin{equation} \left.\begin{aligned} &\varSigma(\boldsymbol{x},t; \varDelta) = \tau_{ij}{S}_{ij}, \\ &\varPsi(\boldsymbol{x},t; \varDelta) ={-}u_i\partial_j \tau_{ij}, \end{aligned}\right\}\end{equation}
\begin{equation} \left.\begin{aligned} &\varSigma(\boldsymbol{x},t; \varDelta) = \tau_{ij}{S}_{ij}, \\ &\varPsi(\boldsymbol{x},t; \varDelta) ={-}u_i\partial_j \tau_{ij}, \end{aligned}\right\}\end{equation}
where the velocity field, the rate-of-strain tensor and ![]() $\tau _{ij}$ are filtered with (4.1) at scale
$\tau _{ij}$ are filtered with (4.1) at scale ![]() $\varDelta$. Both are standard quantities in the analysis of the turbulence cascade (Meneveau & Lund Reference Meneveau and Lund1994; Borue & Orszag Reference Borue and Orszag1998; Aoyama et al. Reference Aoyama, Ishihara, Kaneda, Yokokawa, Itakura and Uno2005; Cardesa et al. Reference Cardesa, Vela-Martín, Dong and Jiménez2015), and are related by
$\varDelta$. Both are standard quantities in the analysis of the turbulence cascade (Meneveau & Lund Reference Meneveau and Lund1994; Borue & Orszag Reference Borue and Orszag1998; Aoyama et al. Reference Aoyama, Ishihara, Kaneda, Yokokawa, Itakura and Uno2005; Cardesa et al. Reference Cardesa, Vela-Martín, Dong and Jiménez2015), and are related by ![]() $\varPsi =\varSigma - \partial _j (u_i\tau _{ij})$. The second term on the right-hand side of this relation is the divergence of an energy flux in physical space, which has zero mean over the computational box, so that
$\varPsi =\varSigma - \partial _j (u_i\tau _{ij})$. The second term on the right-hand side of this relation is the divergence of an energy flux in physical space, which has zero mean over the computational box, so that ![]() $\langle \varSigma \rangle =\langle \varPsi \rangle$. Positive values of
$\langle \varSigma \rangle =\langle \varPsi \rangle$. Positive values of ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$ indicate that the energy is transferred towards the small scales.
$\varPsi$ indicate that the energy is transferred towards the small scales.
Because the decaying system under study is statistically unsteady, averaging over an ensemble of many realisations is required to extract time-dependent statistics. This is generated using the following procedure. All the flow fields in the ensemble share an initial energy spectrum, derived from a forced statistically stationary simulation, and an initial kinetic energy per unit mass. Each field is prepared by randomising the phases of ![]() $\hat {u}_i$, respecting continuity, and integrated for a fixed time
$\hat {u}_i$, respecting continuity, and integrated for a fixed time ![]() $t_{start}$ up to
$t_{start}$ up to ![]() $t_0=0$, where a fully turbulent state is deemed to have been reached, the experiment begins, and statistics start to be compiled. The initial transient,
$t_0=0$, where a fully turbulent state is deemed to have been reached, the experiment begins, and statistics start to be compiled. The initial transient, ![]() $t_{start}$, common to all the elements in the ensemble, is chosen so that
$t_{start}$, common to all the elements in the ensemble, is chosen so that ![]() $t_0$ is beyond the time at which dissipation reaches its maximum, and the turbulent structure of the flow is fully developed. Quantities at
$t_0$ is beyond the time at which dissipation reaches its maximum, and the turbulent structure of the flow is fully developed. Quantities at ![]() $t_0$ are denoted by a ‘0’ subindex. Following this procedure, we generate an ensemble of
$t_0$ are denoted by a ‘0’ subindex. Following this procedure, we generate an ensemble of ![]() $N_s=2000$ realisations, which are evolved on graphic processing units. The statistics below are compiled over all the members of this ensemble.
$N_s=2000$ realisations, which are evolved on graphic processing units. The statistics below are compiled over all the members of this ensemble.
It is found that both the small- and large-scale reference quantities defined above vary little across an ensemble prepared in this way, with a standard deviation of the order of 5 % with respect to their mean.
4.2. Turbulence with a reversible model
The basic numerical experiment is conducted as in Carati et al. (Reference Carati, Winckelmans and Jeanmart2001). After preparing the ensemble of turbulent fields at ![]() $t=t_0=0$, they are evolved for a fixed time
$t=t_0=0$, they are evolved for a fixed time ![]() $t_{inv}$, during which some of the initial energy is exported by the model to the unresolved scales. The simulations are then stopped and the sign of the three components of velocity reversed,
$t_{inv}$, during which some of the initial energy is exported by the model to the unresolved scales. The simulations are then stopped and the sign of the three components of velocity reversed, ![]() $\boldsymbol {u}\rightarrow -\boldsymbol {u}$. The new flow fields are used as the initial conditions for the second part of the run from
$\boldsymbol {u}\rightarrow -\boldsymbol {u}$. The new flow fields are used as the initial conditions for the second part of the run from ![]() $t_{inv}$ to
$t_{inv}$ to ![]() $2t_{inv}$, during which the flows evolve back to their original state, recovering their original energy and the value of other turbulent quantities.
$2t_{inv}$, during which the flows evolve back to their original state, recovering their original energy and the value of other turbulent quantities.
It is found that ![]() $\eta _s$ only changes by 5 % during the decay of the flow, while
$\eta _s$ only changes by 5 % during the decay of the flow, while ![]() $\tau _s$ increases by a factor of
$\tau _s$ increases by a factor of ![]() $1.5$ from
$1.5$ from ![]() $t=0$ to
$t=0$ to ![]() $t_{inv}$. On the other hand, the large-scale quantities
$t_{inv}$. On the other hand, the large-scale quantities ![]() $L$ and
$L$ and ![]() $u'$ vary substantially as the flow decays. The main parameters of the simulations, and the relation between large- and small-scale quantities, are given in table 1.
$u'$ vary substantially as the flow decays. The main parameters of the simulations, and the relation between large- and small-scale quantities, are given in table 1.
Table 1. Main parameters of the simulation averaged over the complete ensemble at time ![]() $t_0=0$ and
$t_0=0$ and ![]() $t_{inv}$. See the text for definitions.
$t_{inv}$. See the text for definitions.

Figure 1(a,b) presents the evolution of the kinetic energy ![]() $\mathcal {E}$ and of
$\mathcal {E}$ and of ![]() $C_s$ as a function of time for a representative experiment. We observe a clear symmetry with respect to
$C_s$ as a function of time for a representative experiment. We observe a clear symmetry with respect to ![]() $t_{inv}$ in both quantities, and we have checked that this symmetry also holds for other turbulent quantities, such as the sub-grid energy fluxes and the skewness of the velocity derivatives. Quantities that are odd with respect to the velocity display odd symmetry in time with respect to
$t_{inv}$ in both quantities, and we have checked that this symmetry also holds for other turbulent quantities, such as the sub-grid energy fluxes and the skewness of the velocity derivatives. Quantities that are odd with respect to the velocity display odd symmetry in time with respect to ![]() $t_{inv}$, and even quantities display even symmetry. In particular, we expect
$t_{inv}$, and even quantities display even symmetry. In particular, we expect ![]() $\boldsymbol {u}(2t_{inv})\simeq -\boldsymbol {u}(0)$.
$\boldsymbol {u}(2t_{inv})\simeq -\boldsymbol {u}(0)$.

Figure 1. Evolution of (a) mean kinetic energy, normalised with the initial energy ![]() $\mathcal {E}_0$, and (b)
$\mathcal {E}_0$, and (b) ![]() $C_s\bar \varDelta ^2$ as a function of time (arbitrary units). The dashed line in (a,b) is
$C_s\bar \varDelta ^2$ as a function of time (arbitrary units). The dashed line in (a,b) is ![]() $t=t_{inv}$, and the dotted lines in (a) are
$t=t_{inv}$, and the dotted lines in (a) are ![]() $t=t_{stats}$, used in § 6. (c) Energy spectrum
$t=t_{stats}$, used in § 6. (c) Energy spectrum ![]() $E(k)$. ——,
$E(k)$. ——, ![]() $t=0$ and
$t=0$ and ![]() $t=2t_{inv}$; – – –,
$t=2t_{inv}$; – – –, ![]() $t=t_{inv}$. The diagonal line is
$t=t_{inv}$. The diagonal line is ![]() $E(k)\propto k^{-5/3}$. (d) Spectrum of the error between the velocity fields at
$E(k)\propto k^{-5/3}$. (d) Spectrum of the error between the velocity fields at ![]() $t=2t_{inv}$ and
$t=2t_{inv}$ and ![]() $t=0$, as a function of wavenumber. The dashed line denotes
$t=0$, as a function of wavenumber. The dashed line denotes ![]() $k^4$.
$k^4$.
Figure 1(c) shows the energy spectrum ![]() $E(k)$ at times
$E(k)$ at times ![]() $t=0$,
$t=0$, ![]() $t_{inv}$ and
$t_{inv}$ and ![]() $2t_{inv}$. Although there are no observable differences between the initial and final spectra, we quantify this difference in scale using the spectrum of the error between the velocity field at
$2t_{inv}$. Although there are no observable differences between the initial and final spectra, we quantify this difference in scale using the spectrum of the error between the velocity field at ![]() $t=0$ and minus the velocity field at
$t=0$ and minus the velocity field at ![]() $2t_{inv}$,
$2t_{inv}$,
which is presented in figure 1(d). The spectrum of the error is of the order of ![]() $0.01$ in the cutoff wavenumber and decreases as
$0.01$ in the cutoff wavenumber and decreases as ![]() $k^4$ with the wavenumber, confirming that the flow fields in the forward and backward evolution are similar, except for the opposite sign and minor differences in the small scales. This suggests that the energy cascade is microscopically reversible in the inertial scales. Sustained reverse cascades are possible in the system, even if only direct ones are observed in practice, supporting the conclusion that the one-directional turbulence cascade is an entropic (probabilistic) effect, unrelated to the presence of an energy sink at the small scales.
$k^4$ with the wavenumber, confirming that the flow fields in the forward and backward evolution are similar, except for the opposite sign and minor differences in the small scales. This suggests that the energy cascade is microscopically reversible in the inertial scales. Sustained reverse cascades are possible in the system, even if only direct ones are observed in practice, supporting the conclusion that the one-directional turbulence cascade is an entropic (probabilistic) effect, unrelated to the presence of an energy sink at the small scales.
This conclusion is in agreement with the empirical evidence that the kinetic energy dissipation in turbulent flows is independent of the Reynolds number (Sreenivasan Reference Sreenivasan1984). This phenomenon, known as the dissipative anomaly, exposes the surrogate nature of kinetic energy dissipation, which is controlled by large-scale dynamics through the energy cascade process (Taylor Reference Taylor1935; Kolmogorov Reference Kolmogorov1941). In agreement with the dissipative anomaly, we will present evidence that the energy dissipation is a consequence, rather than a cause, of the energy cascade.
4.3. The reverse cascade without the model
The validity of the conclusions in the previous section depends on the ability of the model system to represent turbulence dynamics. In particular, since the object of our study is the turbulence cascade rather than the SGS model, it is necessary to assess whether the reversibility properties of the system, and the presence of a sustained backwards energy cascade, stem from the SGS model, or whether intrinsic turbulent mechanisms are involved. In this subsection we show that the model injects energy at the smallest resolved scales, but that the energy travels back to the large scales due to inertial mechanisms. In the next subsection we further demonstrate that the inverse cascade can exist for some time even for irreversible formulations of the sub-grid model.
If the SGS model contributed substantially to the presence of a sustained inverse cascade, its removal during the backward leg of the simulation would have an immediate effect on the system, resulting in the instantaneous breakdown of the reverse cascade. This is shown not to be the case by an experiment in which the model is removed at ![]() $t_{inv}$ by letting
$t_{inv}$ by letting ![]() $C_s=0$. The system then evolves according to the Euler equations
$C_s=0$. The system then evolves according to the Euler equations
 \begin{equation} \left. \begin{aligned} &\partial_t u_i+u_j\partial_j u_i={-}\partial_i p, \\ &\partial_i u_i=0, \end{aligned}\right\}\end{equation}
\begin{equation} \left. \begin{aligned} &\partial_t u_i+u_j\partial_j u_i={-}\partial_i p, \\ &\partial_i u_i=0, \end{aligned}\right\}\end{equation}
which are conservative and include only inertial forces. The resulting evolution of the inertial energy flux across Fourier scales, ![]() $\varPi (k,t)$, defined in (4.4), is displayed in figure 2(a) as a function of wavenumber and time.
$\varPi (k,t)$, defined in (4.4), is displayed in figure 2(a) as a function of wavenumber and time.

Figure 2. (a) Energy flux ![]() $\varPi (k)$ as a function of the time after removing the SGS model,
$\varPi (k)$ as a function of the time after removing the SGS model, ![]() $t/T_0$:
$t/T_0$: ![]() $\square$, solid black line,
$\square$, solid black line, ![]() $0$;
$0$; ![]() $\bullet$, solid red line,
$\bullet$, solid red line, ![]() $0.1$;
$0.1$; ![]() $\blacktriangleright$, solid blue line,
$\blacktriangleright$, solid blue line, ![]() $0.15$;
$0.15$; ![]() $\blacktriangle$, solid magenta line,
$\blacktriangle$, solid magenta line, ![]() $0.25$. Energy flux normalised with
$0.25$. Energy flux normalised with ![]() $\epsilon _0={u'_0}^3/L_0$. (b) Reversal time
$\epsilon _0={u'_0}^3/L_0$. (b) Reversal time ![]() $t_{rev}/T_0$ at which
$t_{rev}/T_0$ at which ![]() $\varPi =0$ as a function of wavenumber
$\varPi =0$ as a function of wavenumber ![]() $kL_0$. Initial condition before the inversion of the velocities and the removal of the model obtained with: ——, red, reversible dynamic SGS model (
$kL_0$. Initial condition before the inversion of the velocities and the removal of the model obtained with: ——, red, reversible dynamic SGS model (![]() $N=128$); – – –, irreversible spectral SGS model (
$N=128$); – – –, irreversible spectral SGS model (![]() $N=512$). The solid black line corresponds to
$N=512$). The solid black line corresponds to ![]() $t_{rev}/T_0=2{(kL_0)}^{-2/3}$.
$t_{rev}/T_0=2{(kL_0)}^{-2/3}$.
At ![]() $t_{inv}$, energy fluxes are negative at all scales and energy flows towards the large scales. Shortly after, at
$t_{inv}$, energy fluxes are negative at all scales and energy flows towards the large scales. Shortly after, at ![]() $t-t_{inv}=0.1T_0$, the inverse cascade begins to break down at the small scales, while it continues to flow backwards across most wavenumbers. This continues to be true at
$t-t_{inv}=0.1T_0$, the inverse cascade begins to break down at the small scales, while it continues to flow backwards across most wavenumbers. This continues to be true at ![]() $t=0.15T_0$, where the direct cascade at the smallest scales coexists with a reverse cascade at the larger scales. The wavenumber separating the two regimes moves progressively towards larger scales, and the whole cascade becomes direct after
$t=0.15T_0$, where the direct cascade at the smallest scales coexists with a reverse cascade at the larger scales. The wavenumber separating the two regimes moves progressively towards larger scales, and the whole cascade becomes direct after ![]() $t\simeq 0.25T_0$.
$t\simeq 0.25T_0$.
Figure 2(b) shows the dependence on the wavenumber of the time ![]() $t_{rev}(k)$ at which
$t_{rev}(k)$ at which ![]() $\varPi (k,t_{rev})=0$. It is significant that, for wavenumbers that can be considered inertial,
$\varPi (k,t_{rev})=0$. It is significant that, for wavenumbers that can be considered inertial, ![]() $kL_0\gg 1$, it follows that
$kL_0\gg 1$, it follows that ![]() $t_{rev}/T_0\approx 2(k L_0)^{-2/3}$, which is consistent with the Kolmogorov (Reference Kolmogorov1941) self-similar structure of the cascade. If we assume a Kolmogorov spectrum,
$t_{rev}/T_0\approx 2(k L_0)^{-2/3}$, which is consistent with the Kolmogorov (Reference Kolmogorov1941) self-similar structure of the cascade. If we assume a Kolmogorov spectrum, ![]() $E(k)=C_K \epsilon _s^{2/3} k^{-5/3}$, where
$E(k)=C_K \epsilon _s^{2/3} k^{-5/3}$, where ![]() $C_K\approx 1.5$ is the Kolmogorov constant (Pope Reference Pope2001) and
$C_K\approx 1.5$ is the Kolmogorov constant (Pope Reference Pope2001) and ![]() $\epsilon _s$ is the energy flux through wavenumber
$\epsilon _s$ is the energy flux through wavenumber ![]() $k$, which is equal to the energy dissipation, the energy above a given wavenumber is
$k$, which is equal to the energy dissipation, the energy above a given wavenumber is
When the SGS model is removed, an inverse cascade can only be sustained by drawing energy from this reservoir. Independently of whether the cascade can maintain its integrity from the informational point of view, the time it takes for a flux ![]() $-\epsilon _s$ to drain (4.8) can be expressed as
$-\epsilon _s$ to drain (4.8) can be expressed as
 \begin{equation} \frac{t_{max}}{T_0}\approx \frac{3}{2} C_K \left( \frac{u'^3}{L_0\epsilon_s} \right)^{1/3} (k L_0)^{{-}2/3} \approx 2 (k L_0)^{{-}2/3}, \end{equation}
\begin{equation} \frac{t_{max}}{T_0}\approx \frac{3}{2} C_K \left( \frac{u'^3}{L_0\epsilon_s} \right)^{1/3} (k L_0)^{{-}2/3} \approx 2 (k L_0)^{{-}2/3}, \end{equation}where we have used values from table 2. As shown in figure 2(b), this approximation is only 50 % larger than the observed reversal time for the initial conditions prepared with the reversible SGS model.
Table 2. Auto-correlation coefficient among scales of ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$, evaluated for: ‘All’, the complete field; ‘
$\varPsi$, evaluated for: ‘All’, the complete field; ‘![]() $+$’, conditioned to positive energy transfer events at
$+$’, conditioned to positive energy transfer events at ![]() $5\varDelta _g$; ‘
$5\varDelta _g$; ‘![]() $-$’, conditioned to negative energy transfer events at
$-$’, conditioned to negative energy transfer events at ![]() $5\varDelta _g$.
$5\varDelta _g$.
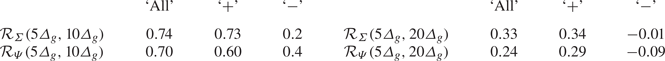
The simplest conclusion is that the model just acts as a source to provide the small scales with energy as they are being depleted by the flux towards larger eddies. If this source is missing, the predominant forward cascade reappears, but the inertial mechanisms are able to maintain the reverse cascade process as long as energy is available.
4.4. The effect of irreversible models
We have repeated the same experiment for an irreversible spectral SGS model (Métais & Lesieur Reference Métais and Lesieur1992) with a higher resolution ![]() $(N=512)$. Results of
$(N=512)$. Results of ![]() $t_{rev}(k)$ for this experiment are shown by the dashed line in figure 2(b). The behaviour is similar to the experiment in the previous section, but the wider separation of scales in this simulation allows the preservation of an inverse cascade for times of the order of the integral time. This experiment confirms that the microscopic reversibility of the inertial scales is independent of the type of dissipation, and holds as long as the information of the direct cascade process is not destroyed by the LES model. This experiment suggests that microscopic reversibility should also hold in the inertial range of fully developed Navier–Stokes turbulence. Note that the good agreement of the reversal time with the energy estimate in (4.9) implies that
$t_{rev}(k)$ for this experiment are shown by the dashed line in figure 2(b). The behaviour is similar to the experiment in the previous section, but the wider separation of scales in this simulation allows the preservation of an inverse cascade for times of the order of the integral time. This experiment confirms that the microscopic reversibility of the inertial scales is independent of the type of dissipation, and holds as long as the information of the direct cascade process is not destroyed by the LES model. This experiment suggests that microscopic reversibility should also hold in the inertial range of fully developed Navier–Stokes turbulence. Note that the good agreement of the reversal time with the energy estimate in (4.9) implies that ![]() $t_{rev}$ is very close to the maximum possible for a given energy.
$t_{rev}$ is very close to the maximum possible for a given energy.
5. Phase- and physical-space characterisation of the energy cascade
5.1. The geometry of phase space
In the first place we confirm, by perturbing the inverse cascade, that in the neighbourhood of each inverse evolution there exist a dense distribution of phase-space trajectories that also display inverse dynamics. Each inverse trajectory is ‘unstable’, in the sense that it is eventually destroyed when perturbed, but inverse dynamics is easily found considerably far from the original phase-space trajectories, even for distances of the order of the size of the accessible phase space, suggesting that inverse and direct trajectories lie in separated regions of phase space, rather than mostly being intertwined in the same neighbourhood. Hereafter we refer to the phase space of the Fourier coefficients, and consider, unless stated, experiments with the reversible SGS model.
In this experiment we generate a backwards initial condition by integrating the equations of motion until ![]() $t_{inv}$, changing the sign of the velocities
$t_{inv}$, changing the sign of the velocities ![]() $\boldsymbol {u}^\iota =-\boldsymbol {u}(t_{inv})$, and introducing a perturbation,
$\boldsymbol {u}^\iota =-\boldsymbol {u}(t_{inv})$, and introducing a perturbation, ![]() $\delta \boldsymbol {u}$. The perturbed flow field,
$\delta \boldsymbol {u}$. The perturbed flow field, ![]() $\boldsymbol {u}^p=\boldsymbol {u}^\iota +\delta \boldsymbol {u}$, is evolved and compared with the unperturbed trajectory,
$\boldsymbol {u}^p=\boldsymbol {u}^\iota +\delta \boldsymbol {u}$, is evolved and compared with the unperturbed trajectory, ![]() $\boldsymbol {u}^\iota (t)$. We choose the initial perturbation field in Fourier space as
$\boldsymbol {u}^\iota (t)$. We choose the initial perturbation field in Fourier space as
where ![]() $\phi$ is a random angle with uniform distribution between
$\phi$ is a random angle with uniform distribution between ![]() $0$ and
$0$ and ![]() $2{\rm \pi}$ and
$2{\rm \pi}$ and ![]() $\mu$ is a real parameter that sets the initial energy of the perturbation. The same
$\mu$ is a real parameter that sets the initial energy of the perturbation. The same ![]() $\phi$ is used for the three velocity components, so that incompressibility also holds for
$\phi$ is used for the three velocity components, so that incompressibility also holds for ![]() $\boldsymbol {u}^p$. Figure 3(a,b) shows the evolution of the mean kinetic energy of the perturbed field,
$\boldsymbol {u}^p$. Figure 3(a,b) shows the evolution of the mean kinetic energy of the perturbed field, ![]() $\mathcal{E}_p=\langle u^p\rangle^2/2$, and of the perturbation field,
$\mathcal{E}_p=\langle u^p\rangle^2/2$, and of the perturbation field, ![]() $\delta \mathcal {E}=\langle \delta \boldsymbol {u}^2\rangle /{2}$, for
$\delta \mathcal {E}=\langle \delta \boldsymbol {u}^2\rangle /{2}$, for ![]() $\mu =0.1$,
$\mu =0.1$, ![]() $0.01$ and
$0.01$ and ![]() $0.001$. The energy of the perturbed fields increases for a considerable time in the three cases, demonstrating the presence of inverse energy transfer and negative mean eddy viscosity,
$0.001$. The energy of the perturbed fields increases for a considerable time in the three cases, demonstrating the presence of inverse energy transfer and negative mean eddy viscosity, ![]() $C_s<0$. Even under the strongest initial perturbation,
$C_s<0$. Even under the strongest initial perturbation, ![]() $\mu =0.1$, the inverse cascade is sustained for approximately
$\mu =0.1$, the inverse cascade is sustained for approximately ![]() $0.5T_0$. Note that
$0.5T_0$. Note that ![]() $\delta \mathcal {E}$ grows exponentially at a constant rate for some time under the linearised dynamics of the system, indicating that perturbations tend to the most unstable linear perturbation (Benettin et al. Reference Benettin, Galgani, Giorgilli and Strelcyn1980), which is independent of the form of the initial perturbation.
$\delta \mathcal {E}$ grows exponentially at a constant rate for some time under the linearised dynamics of the system, indicating that perturbations tend to the most unstable linear perturbation (Benettin et al. Reference Benettin, Galgani, Giorgilli and Strelcyn1980), which is independent of the form of the initial perturbation.

Figure 3. (a) Evolution of the energy of the perturbed fields ![]() $\mathcal {E}_p$ and (b) of
$\mathcal {E}_p$ and (b) of ![]() $\delta \mathcal {E}=1/2\langle \delta {\boldsymbol {u}}^2\rangle$, normalised with
$\delta \mathcal {E}=1/2\langle \delta {\boldsymbol {u}}^2\rangle$, normalised with ![]() $\mathcal {E}_0$, for: ——,
$\mathcal {E}_0$, for: ——, ![]() $\mu =0.1$; – – –, red,
$\mu =0.1$; – – –, red, ![]() $\mu =0.01$;
$\mu =0.01$; ![]() $-\cdot -$, blue,
$-\cdot -$, blue, ![]() $\mu =0.001$;
$\mu =0.001$; ![]() $\cdots \cdots \cdot$, energy of the unperturbed trajectory,
$\cdots \cdots \cdot$, energy of the unperturbed trajectory, ![]() $\mathcal {E}(t)/\mathcal {E}_0$. (c) Perturbed trajectories for
$\mathcal {E}(t)/\mathcal {E}_0$. (c) Perturbed trajectories for ![]() $\mu =0.1$ and
$\mu =0.1$ and ![]() $\mu =0.01$, represented in the energy-dissipation space. Symbols as in (a). The solid circle represents the beginning of the inverse trajectory at
$\mu =0.01$, represented in the energy-dissipation space. Symbols as in (a). The solid circle represents the beginning of the inverse trajectory at ![]() $t_{inv}$, the empty circles represent the end of the perturbed trajectories at
$t_{inv}$, the empty circles represent the end of the perturbed trajectories at ![]() $2t_{inv}$, and the solid square represents the end of the direct trajectory at time
$2t_{inv}$, and the solid square represents the end of the direct trajectory at time ![]() $t_{inv}$. The dotted lines and arrows represent the direct and inverse trajectories. (d) Evolution of the probability density function of
$t_{inv}$. The dotted lines and arrows represent the direct and inverse trajectories. (d) Evolution of the probability density function of ![]() $\epsilon _s$ as a function of time starting from random initial conditions at
$\epsilon _s$ as a function of time starting from random initial conditions at ![]() $t_{start}$. From left to right:
$t_{start}$. From left to right: ![]() $(t-t_{start})/T_0=: 0.0$;
$(t-t_{start})/T_0=: 0.0$; ![]() $0.008$;
$0.008$; ![]() $0.017$;
$0.017$; ![]() $0.033$;
$0.033$; ![]() $0.067$;
$0.067$; ![]() $1.0$.
$1.0$. ![]() $\epsilon _s$ normalised with the ensemble average at
$\epsilon _s$ normalised with the ensemble average at ![]() $T_0$.
$T_0$.
As shown in figure 3(b), by the time the inverse cascade is destroyed and the energy of the perturbed fields has evolved to a maximum and ![]() $C_s=0$, the energy of the perturbation is comparable to the total energy in all cases,
$C_s=0$, the energy of the perturbation is comparable to the total energy in all cases, ![]() $\delta \mathcal {E}\sim \mathcal {E}$, which indicates that the states that separate inverse and direct dynamics are considerably far in phase space from the unperturbed trajectories, at least when the initial perturbations are small. If we estimate distances as the square root of the energy (
$\delta \mathcal {E}\sim \mathcal {E}$, which indicates that the states that separate inverse and direct dynamics are considerably far in phase space from the unperturbed trajectories, at least when the initial perturbations are small. If we estimate distances as the square root of the energy (![]() $L_2$ norm of the velocity field), the maximum of
$L_2$ norm of the velocity field), the maximum of ![]() $\mathcal {E}_p$ is located approximately at
$\mathcal {E}_p$ is located approximately at ![]() $\delta \mathcal {E}^{1/2}\simeq 0.4\mathcal {E}_0^{1/2}$ from the unperturbed phase-space trajectory. In figure 3(c) we represent the evolution of the perturbed trajectories in the dissipation-energy space. This plot intuitively shows that a typical direct trajectory is located far apart in phase space from inverse trajectories, and that perturbed inverse trajectories must first cross the set of states with zero dissipation,
$\delta \mathcal {E}^{1/2}\simeq 0.4\mathcal {E}_0^{1/2}$ from the unperturbed phase-space trajectory. In figure 3(c) we represent the evolution of the perturbed trajectories in the dissipation-energy space. This plot intuitively shows that a typical direct trajectory is located far apart in phase space from inverse trajectories, and that perturbed inverse trajectories must first cross the set of states with zero dissipation, ![]() $C_s=0$, before developing a direct cascade.
$C_s=0$, before developing a direct cascade.
In figure 3(d) we show the evolution of the probability density function of the sub-grid energy transfer, ![]() $\epsilon _s$, in the direct evolution of the ensemble, starting at
$\epsilon _s$, in the direct evolution of the ensemble, starting at ![]() $t_{start}$, when the initial condition is a random field with a prescribed energy spectrum. The initial probability distribution of
$t_{start}$, when the initial condition is a random field with a prescribed energy spectrum. The initial probability distribution of ![]() $\epsilon _s$ is symmetric and has zero mean, indicating that the probabilities of direct and inverse evolutions are similar. As the system evolves in time and develops the turbulence structure, the probability of finding a negative value of
$\epsilon _s$ is symmetric and has zero mean, indicating that the probabilities of direct and inverse evolutions are similar. As the system evolves in time and develops the turbulence structure, the probability of finding a negative value of ![]() $\epsilon _s$ decreases drastically. At
$\epsilon _s$ decreases drastically. At ![]() $t-t_{start}=0.008T_0$, we do not observe any negative values of
$t-t_{start}=0.008T_0$, we do not observe any negative values of ![]() $\epsilon _s$ in the ensemble. The standard deviation of
$\epsilon _s$ in the ensemble. The standard deviation of ![]() $\epsilon _s$ is small compared with the mean at
$\epsilon _s$ is small compared with the mean at ![]() $t-t_{start}=T_0$, which indicates the negligible probability of observing negative values of
$t-t_{start}=T_0$, which indicates the negligible probability of observing negative values of ![]() $\epsilon _s$ after a time of the order of an eddy-turnover time.
$\epsilon _s$ after a time of the order of an eddy-turnover time.
Although decaying turbulent flows have no attractor in the strict sense, i.e. a set of phase-space points to which the system is attracted and where it remains during its evolution, we use the term here to denote the set of phase-space trajectories with a fully turbulent structure and a direct energy cascade. As we have shown, this set of states is in fact ‘attracting’, but the flow does not remain indefinitely turbulent due to its decaying nature. Let us note that it is possible to construct a reversible turbulent system with a proper turbulent attractor by including a reversible forcing in the large scales, for instance, a linear forcing that keeps the total energy of the system constant in time.
Inverse evolutions sustained in time are almost only accessible from forward-evolved flow fields with changed sign. These trajectories lie in the antiattractor, which is constructed by applying the transformation ![]() $\boldsymbol {u}\rightarrow -\boldsymbol {u}$ to the turbulent attractor. However, we have shown in this analysis that inverse trajectories exist in a larger set of states outside the antiattractor, which can be escaped by perturbing the reversed flow fields. The destruction of the inverse cascade under perturbations reflects the negligible probability of inverse evolutions, and indicates that they can only be accessed temporarily. Moreover, the small standard deviation of the sub-grid energy transfer with respect to the mean in the turbulent attractor reflects the negligible probability that the system spontaneously escapes the attractor and develops and inverse energy cascade.
$\boldsymbol {u}\rightarrow -\boldsymbol {u}$ to the turbulent attractor. However, we have shown in this analysis that inverse trajectories exist in a larger set of states outside the antiattractor, which can be escaped by perturbing the reversed flow fields. The destruction of the inverse cascade under perturbations reflects the negligible probability of inverse evolutions, and indicates that they can only be accessed temporarily. Moreover, the small standard deviation of the sub-grid energy transfer with respect to the mean in the turbulent attractor reflects the negligible probability that the system spontaneously escapes the attractor and develops and inverse energy cascade.
The reversible turbulent system under study provides access to trajectories outside the turbulence attractor, which contains almost exclusively direct cascades. By studying these inverse trajectories, we identify the physical mechanisms that lead to the prevalence of direct over inverse cascades.
5.2. The structure of local energy fluxes in physical space
Up to now we have only dealt with the mean transfer of energy over the complete domain. In this section we characterise the energy cascade as a local process in physical space. We study here two markers of local energy transfer in physical space, ![]() $\varSigma (\boldsymbol {x},t;\varDelta )$ and
$\varSigma (\boldsymbol {x},t;\varDelta )$ and ![]() $\varPsi (\boldsymbol {x},t;\varDelta )$, previously defined in (4.5), calculated at filter scales
$\varPsi (\boldsymbol {x},t;\varDelta )$, previously defined in (4.5), calculated at filter scales ![]() $\varDelta =5\varDelta _{g}$ and
$\varDelta =5\varDelta _{g}$ and ![]() $\varDelta =10\varDelta _{g}$. Figure 4(a,b) show the probability distribution of these quantities in the direct evolution. We observe wide tails in the probability distribution of the two quantities, and skewness towards positive events, which is more pronounced for
$\varDelta =10\varDelta _{g}$. Figure 4(a,b) show the probability distribution of these quantities in the direct evolution. We observe wide tails in the probability distribution of the two quantities, and skewness towards positive events, which is more pronounced for ![]() $\varSigma$ than for
$\varSigma$ than for ![]() $\varPsi$. Energy fluxes change sign under
$\varPsi$. Energy fluxes change sign under ![]() $\boldsymbol {u}\rightarrow -\boldsymbol {u}$, and, as shown in figure 4, their odd-order moments are in general non-zero and have a definite sign in turbulent flows. This sign denotes statistical irreversibility, i.e, the privileged temporal direction of the system in an out-of-equilibrium evolution. The spatial average, which marks the direction of the cascade, is an important example,
$\boldsymbol {u}\rightarrow -\boldsymbol {u}$, and, as shown in figure 4, their odd-order moments are in general non-zero and have a definite sign in turbulent flows. This sign denotes statistical irreversibility, i.e, the privileged temporal direction of the system in an out-of-equilibrium evolution. The spatial average, which marks the direction of the cascade, is an important example, ![]() $\langle \varSigma \rangle =\langle \varPsi \rangle >0$.
$\langle \varSigma \rangle =\langle \varPsi \rangle >0$.

Figure 4. (a,b) Probability density function of local markers of the energy cascade without volume averaging: (a) ![]() $\varSigma$; (b)
$\varSigma$; (b) ![]() $\varPsi$. Symbols correspond to:
$\varPsi$. Symbols correspond to: ![]() $\blacktriangle$, dashed red line,
$\blacktriangle$, dashed red line, ![]() $\varSigma (5\varDelta _{g})$;
$\varSigma (5\varDelta _{g})$; ![]() $\blacksquare$, dashed blue line,
$\blacksquare$, dashed blue line, ![]() $\varSigma (10\varDelta _{g})$;
$\varSigma (10\varDelta _{g})$; ![]() $\blacktriangleright$, solid magenta line,
$\blacktriangleright$, solid magenta line, ![]() $\varPsi (5\varDelta _{g})$;
$\varPsi (5\varDelta _{g})$; ![]() $\bullet$, solid black line,
$\bullet$, solid black line, ![]() $\varPsi (10\varDelta _{g})$. The dashed–dotted lines represent
$\varPsi (10\varDelta _{g})$. The dashed–dotted lines represent ![]() $-\langle \psi \rangle /\sigma _V$ for quantities calculated at
$-\langle \psi \rangle /\sigma _V$ for quantities calculated at ![]() $5\varDelta _{g}$, and the open symbols represent the probability density function of
$5\varDelta _{g}$, and the open symbols represent the probability density function of ![]() $\langle \varSigma (5\varDelta _{g})\rangle _V$ and
$\langle \varSigma (5\varDelta _{g})\rangle _V$ and ![]() $\langle \varPsi (5\varDelta _{g})\rangle _V$ for
$\langle \varPsi (5\varDelta _{g})\rangle _V$ for ![]() $V=(16\varDelta _{g})^3$.
$V=(16\varDelta _{g})^3$.
To characterise the non-local spatial properties of the local energy fluxes, we define the correlation coefficient between two scalar fields, ![]() $\psi$ and
$\psi$ and ![]() $\zeta$, as
$\zeta$, as
where we subtract the spatial average from quantities marked with primes. Due to isotropy, ![]() $\mathcal {S}$ only depends on the spatial distance,
$\mathcal {S}$ only depends on the spatial distance, ![]() $\Delta x=|\Delta \boldsymbol {x}|$. We also define the auto-correlation coefficient
$\Delta x=|\Delta \boldsymbol {x}|$. We also define the auto-correlation coefficient ![]() $\mathcal {S}_{\psi ,\psi }(\Delta x)$ and the auto-correlation length as
$\mathcal {S}_{\psi ,\psi }(\Delta x)$ and the auto-correlation length as
which measures the typical length over which ![]() $\psi$ decorrelates, and is related to the typical size of events in
$\psi$ decorrelates, and is related to the typical size of events in ![]() $\psi$. The correlation lengths of
$\psi$. The correlation lengths of ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$ are proportional to the filter size
$\varPsi$ are proportional to the filter size ![]() $\varDelta$,
$\varDelta$, ![]() $\ell _\varSigma =0.47 \varDelta$ and
$\ell _\varSigma =0.47 \varDelta$ and ![]() $\ell _\varPsi =0.51 \varDelta$.
$\ell _\varPsi =0.51 \varDelta$.
We use ![]() $\langle \varSigma \rangle _V$ and
$\langle \varSigma \rangle _V$ and ![]() $\langle \varPsi \rangle _V$ to study the spatial structure of energy fluxes, where
$\langle \varPsi \rangle _V$ to study the spatial structure of energy fluxes, where ![]() $\langle \cdot \rangle _V$ represents the volume-averaging operation over a sphere of volume
$\langle \cdot \rangle _V$ represents the volume-averaging operation over a sphere of volume ![]() $V$. The standard deviation of the probability distribution of the volume-averaged fields,
$V$. The standard deviation of the probability distribution of the volume-averaged fields,
is shown in figure 5(a) as a function of the averaging volume, where ![]() $\sigma _0=(\langle \psi ^2\rangle - \langle \psi \rangle ^2)^{1/2}$ is the standard deviation of the test field without volume averaging. When the averaging volume is sufficiently large,
$\sigma _0=(\langle \psi ^2\rangle - \langle \psi \rangle ^2)^{1/2}$ is the standard deviation of the test field without volume averaging. When the averaging volume is sufficiently large, ![]() $V/\ell ^3\gtrsim 10^3$, the standard deviation becomes inversely proportional to the square root of
$V/\ell ^3\gtrsim 10^3$, the standard deviation becomes inversely proportional to the square root of ![]() $\mathcal {N}=V/\ell ^3$ in all cases, where
$\mathcal {N}=V/\ell ^3$ in all cases, where ![]() $\mathcal {N}$ is a measure of the number of independent energy transfer events within the averaging volume. These results suggest statistical independence of the events within the averaging volumes and some degree of space locality in the energy cascade.
$\mathcal {N}$ is a measure of the number of independent energy transfer events within the averaging volume. These results suggest statistical independence of the events within the averaging volumes and some degree of space locality in the energy cascade.

Figure 5. (a) Plot of ![]() $\sigma _V$ as a function of
$\sigma _V$ as a function of ![]() $V/\ell ^3$, where the dashed line represents
$V/\ell ^3$, where the dashed line represents ![]() $\sigma _V\sim \mathcal {N}^{-1/2}$. Symbols correspond to:
$\sigma _V\sim \mathcal {N}^{-1/2}$. Symbols correspond to: ![]() $\blacktriangle$, dashed red line,
$\blacktriangle$, dashed red line, ![]() $\varSigma (5\varDelta _{g})$;
$\varSigma (5\varDelta _{g})$; ![]() $\blacksquare$, dashed blue line,
$\blacksquare$, dashed blue line, ![]() $\varSigma (10\varDelta _{g})$;
$\varSigma (10\varDelta _{g})$; ![]() $\blacktriangleright$, solid magenta line,
$\blacktriangleright$, solid magenta line, ![]() $\varPsi (5\varDelta _{g})$;
$\varPsi (5\varDelta _{g})$; ![]() $\bullet$, dashed black line,
$\bullet$, dashed black line, ![]() $\varPsi (10\varDelta _{g})$. (b) Correlation coefficient between
$\varPsi (10\varDelta _{g})$. (b) Correlation coefficient between ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$ as a function of the averaging volume:
$\varPsi$ as a function of the averaging volume: ![]() $\blacksquare$, solid dash red,
$\blacksquare$, solid dash red, ![]() $\mathcal {S}_{\langle \varSigma \rangle _V,\langle \varPsi \rangle _V}(0)$ at
$\mathcal {S}_{\langle \varSigma \rangle _V,\langle \varPsi \rangle _V}(0)$ at ![]() $5\varDelta _{g}$;
$5\varDelta _{g}$; ![]() $\bullet$, solid blue line,
$\bullet$, solid blue line, ![]() $\mathcal {S}_{\langle \varSigma \rangle _V,\langle \varPsi \rangle _V}(0)$ at
$\mathcal {S}_{\langle \varSigma \rangle _V,\langle \varPsi \rangle _V}(0)$ at ![]() $10\varDelta _{g}$. Error bars are calculated from the average standard deviation of
$10\varDelta _{g}$. Error bars are calculated from the average standard deviation of ![]() $\log \mathcal {P}$ when partitioning the complete dataset in four subsets. (c) Interscale auto-correlation coefficient as a function of the averaging volume:
$\log \mathcal {P}$ when partitioning the complete dataset in four subsets. (c) Interscale auto-correlation coefficient as a function of the averaging volume: ![]() $\blacktriangle$, solid black line,
$\blacktriangle$, solid black line, ![]() $\mathcal {R}_{\langle \varSigma \rangle _V}(5\varDelta _{g},10\varDelta _{g})$;
$\mathcal {R}_{\langle \varSigma \rangle _V}(5\varDelta _{g},10\varDelta _{g})$; ![]() $\blacktriangleright$, solid magenta line,
$\blacktriangleright$, solid magenta line, ![]() $\mathcal {R}_{\langle \varPsi \rangle _V}(5\varDelta _{g},10\varDelta _{g})$;
$\mathcal {R}_{\langle \varPsi \rangle _V}(5\varDelta _{g},10\varDelta _{g})$; ![]() $\blacktriangle$, dashed black line,
$\blacktriangle$, dashed black line, ![]() $\mathcal {R}^-_{\langle \varSigma \rangle _V}(5\varDelta _{g},10\varDelta _{g})$;
$\mathcal {R}^-_{\langle \varSigma \rangle _V}(5\varDelta _{g},10\varDelta _{g})$; ![]() $\blacktriangleright$, solid dash magenta,
$\blacktriangleright$, solid dash magenta, ![]() $\mathcal {R}^-_{\langle \varPsi \rangle _V}(5\varDelta _{g},10\varDelta _{g})$. (d) Asymmetry function,
$\mathcal {R}^-_{\langle \varPsi \rangle _V}(5\varDelta _{g},10\varDelta _{g})$. (d) Asymmetry function, ![]() $\mathcal {P}$, as a function of
$\mathcal {P}$, as a function of ![]() $\langle \psi \rangle ^2/\sigma ^2_V$. Symbols as in (a). The dashed line is the exact solution of
$\langle \psi \rangle ^2/\sigma ^2_V$. Symbols as in (a). The dashed line is the exact solution of ![]() $\mathcal {P}$ for a Gaussian, which approaches
$\mathcal {P}$ for a Gaussian, which approaches ![]() $\log \mathcal {P}=1/2{\langle \psi \rangle ^2}/{\sigma _V^2}$ for large
$\log \mathcal {P}=1/2{\langle \psi \rangle ^2}/{\sigma _V^2}$ for large ![]() ${\langle \psi \rangle ^2}/{\sigma _V^2}$. (e, f) Probability density function of local markers of the energy cascade averaged at scale
${\langle \psi \rangle ^2}/{\sigma _V^2}$. (e, f) Probability density function of local markers of the energy cascade averaged at scale ![]() $V^{1/3}=1.2L_0=32\varDelta _g$: (e)
$V^{1/3}=1.2L_0=32\varDelta _g$: (e) ![]() $\varSigma$; ( f)
$\varSigma$; ( f) ![]() $\varPsi$. The dashed–dotted lines represent
$\varPsi$. The dashed–dotted lines represent ![]() $-\langle \psi \rangle /\sigma _V$ for quantities calculated at
$-\langle \psi \rangle /\sigma _V$ for quantities calculated at ![]() $5\varDelta _{g}$. Symbols as in (a).
$5\varDelta _{g}$. Symbols as in (a).
Despite this locality, ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$ are very different pointwise, which might suggest that local energy fluxes are not uniquely defined, and that only global averages are robust with respect to the particular definition of fluxes,
$\varPsi$ are very different pointwise, which might suggest that local energy fluxes are not uniquely defined, and that only global averages are robust with respect to the particular definition of fluxes, ![]() $\langle \varSigma \rangle =\langle \varPsi \rangle$. In fact, the correlation between
$\langle \varSigma \rangle =\langle \varPsi \rangle$. In fact, the correlation between ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$ for
$\varPsi$ for ![]() $\Delta x=0$ is low,
$\Delta x=0$ is low, ![]() $\mathcal {S}_{\varSigma ,\varPsi }(0)\sim 0.05$, at both filter scales,
$\mathcal {S}_{\varSigma ,\varPsi }(0)\sim 0.05$, at both filter scales, ![]() $5\varDelta _{g}$ and
$5\varDelta _{g}$ and ![]() $10\varDelta _{g}$. However, when these quantities are averaged, the correlation coefficient increases rapidly with the averaging volume. In figure 5(b) we show the dependence of
$10\varDelta _{g}$. However, when these quantities are averaged, the correlation coefficient increases rapidly with the averaging volume. In figure 5(b) we show the dependence of ![]() $\mathcal {S}_{\langle \varSigma \rangle _V, \langle \varPsi \rangle _V}(0)$ on
$\mathcal {S}_{\langle \varSigma \rangle _V, \langle \varPsi \rangle _V}(0)$ on ![]() $V$. For averaging volumes
$V$. For averaging volumes ![]() $V\sim (4\ell )^3$, the correlation increases to approximately
$V\sim (4\ell )^3$, the correlation increases to approximately ![]() $0.7$ for both filter widths, indicating that
$0.7$ for both filter widths, indicating that ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$ are similar when averaged over volumes of the order of their cubed correlation length.
$\varPsi$ are similar when averaged over volumes of the order of their cubed correlation length.
5.3. The structure of local energy fluxes in scale space
We extend this analysis to scale space by considering the correlation of the energy fluxes at different scales, defined as
and calculate the same quantity conditioning the averages to positive or negative energy transfer events at scale ![]() $\varDelta _1$. We denote the conditional correlations by
$\varDelta _1$. We denote the conditional correlations by ![]() $\mathcal {R}^+$ when conditioning to
$\mathcal {R}^+$ when conditioning to ![]() $\psi (\varDelta _1)>0$, and
$\psi (\varDelta _1)>0$, and ![]() $\mathcal {R}^-$ when conditioning to
$\mathcal {R}^-$ when conditioning to ![]() $\psi (\varDelta _1)<0$. These interscale auto-correlation coefficients are presented in table 2. We find correlation values of approximately
$\psi (\varDelta _1)<0$. These interscale auto-correlation coefficients are presented in table 2. We find correlation values of approximately ![]() $0.7$ for scale increments of
$0.7$ for scale increments of ![]() $2$ in both quantities. Table 2 also includes results for
$2$ in both quantities. Table 2 also includes results for ![]() $\varDelta _2=20\varDelta _g$. It shows that all fluxes substantially decorrelate for
$\varDelta _2=20\varDelta _g$. It shows that all fluxes substantially decorrelate for ![]() $\varDelta _2/\varDelta _1=4$ (Cardesa et al. Reference Cardesa, Vela-Martín and Jiménez2017), and that this is especially true for the backscatter.
$\varDelta _2/\varDelta _1=4$ (Cardesa et al. Reference Cardesa, Vela-Martín and Jiménez2017), and that this is especially true for the backscatter.
Figure 5(c) shows the dependence of ![]() $\mathcal {R}_{\langle \varSigma \rangle _V}(5\varDelta _{g}, 10\varDelta _{g})$ and
$\mathcal {R}_{\langle \varSigma \rangle _V}(5\varDelta _{g}, 10\varDelta _{g})$ and ![]() $\mathcal {R}_{\langle \varPsi \rangle _V}(5\varDelta _{g},10\varDelta _{g})$ on the averaging volume
$\mathcal {R}_{\langle \varPsi \rangle _V}(5\varDelta _{g},10\varDelta _{g})$ on the averaging volume ![]() $V$. The interscale auto-correlation increases with the averaging volume when we consider all direct events (not shown). On the other hand, the correlations conditioned to backscatter increase up to volumes of the order of
$V$. The interscale auto-correlation increases with the averaging volume when we consider all direct events (not shown). On the other hand, the correlations conditioned to backscatter increase up to volumes of the order of ![]() $V^{1/3}\approx 2\ell$, and then decrease. Beyond
$V^{1/3}\approx 2\ell$, and then decrease. Beyond ![]() $V^{1/3}\approx 4\ell$, the number of averaged inverse energy transfer events is not enough to compute reliable correlations.
$V^{1/3}\approx 4\ell$, the number of averaged inverse energy transfer events is not enough to compute reliable correlations.
5.4. Physical-space estimates of the probability of inverse cascades
We have shown in § 5.1 that the probability of spontaneously observing an inverse cascade over extended regions of a turbulent flow is negligible, making it impractical to quantify the probability of such evolutions by direct observation. However, as shown in § 5.2, we frequently observe local inverse energy transfer events over restricted regions of physical space. We attempt to estimate the probability of observing an inverse cascade using the integral asymmetry function,
which compares the probability of observing a direct to an inverse cascade in a volume ![]() $V$. This approach follows the methodology of the fluctuation relations (Evans & Searles Reference Evans and Searles2002) and its local versions (Ayton, Evans & Searles Reference Ayton, Evans and Searles2001; Michel & Searles Reference Michel and Searles2013).
$V$. This approach follows the methodology of the fluctuation relations (Evans & Searles Reference Evans and Searles2002) and its local versions (Ayton, Evans & Searles Reference Ayton, Evans and Searles2001; Michel & Searles Reference Michel and Searles2013).
We evaluate the integral asymmetry function of ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$ for different averaging volumes, and display it as a function of
$\varPsi$ for different averaging volumes, and display it as a function of ![]() $\langle \psi \rangle ^2/\sigma _V^2$ in figure 5(d). The statistical independence of the energy transfer events reported in § 5.2 suggests that, when the averaging volume is large enough, the integral asymmetry function should behave as that of a Gaussian distribution with non-zero mean, which for large
$\langle \psi \rangle ^2/\sigma _V^2$ in figure 5(d). The statistical independence of the energy transfer events reported in § 5.2 suggests that, when the averaging volume is large enough, the integral asymmetry function should behave as that of a Gaussian distribution with non-zero mean, which for large ![]() $\langle \psi \rangle ^2/\sigma _V^2$ is
$\langle \psi \rangle ^2/\sigma _V^2$ is
If we assume that the number of independent events in a volume ![]() $V$ is
$V$ is ![]() $\mathcal {N}\sim V/\ell ^3$, we can conclude that
$\mathcal {N}\sim V/\ell ^3$, we can conclude that ![]() $\log P \sim \mathcal {N} \sim V/\ell ^3$, and the probability of direct over inverse cascades increases exponentially with the number of independent energy transfer events considered. The exponential dependence in (5.7) is well satisfied in figure 5(d), but the prefactor is not, and
$\log P \sim \mathcal {N} \sim V/\ell ^3$, and the probability of direct over inverse cascades increases exponentially with the number of independent energy transfer events considered. The exponential dependence in (5.7) is well satisfied in figure 5(d), but the prefactor is not, and ![]() $\log \mathcal {P}>2\langle \psi \rangle ^2/\sigma _V^2$. Since the prefactor is a property of the Gaussian distributions that arise from the application of the central limit theorem, this failure can be traced to the strong dependence of
$\log \mathcal {P}>2\langle \psi \rangle ^2/\sigma _V^2$. Since the prefactor is a property of the Gaussian distributions that arise from the application of the central limit theorem, this failure can be traced to the strong dependence of ![]() $\mathcal {P}$ on the negative tails of the statistical distributions of
$\mathcal {P}$ on the negative tails of the statistical distributions of ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$, which are not Gaussian. The fast growth of
$\varPsi$, which are not Gaussian. The fast growth of ![]() $\log \mathcal {P}$ in figure 5(d) signals that the probability of inverse-transfer events decreases with volume averaging faster than what could be expected for independent events, in agreement with the evidence in figure 5(c) that inverse energy transfer is shallow in scale space. In figure 4(a,b) we show the probability density function of
$\log \mathcal {P}$ in figure 5(d) signals that the probability of inverse-transfer events decreases with volume averaging faster than what could be expected for independent events, in agreement with the evidence in figure 5(c) that inverse energy transfer is shallow in scale space. In figure 4(a,b) we show the probability density function of ![]() $\langle \varSigma (5\varDelta _g) \rangle _V$ and
$\langle \varSigma (5\varDelta _g) \rangle _V$ and ![]() $\langle \varSigma (5\varDelta _g) \rangle _V$ for
$\langle \varSigma (5\varDelta _g) \rangle _V$ for ![]() $V=(16\varDelta _g)^3$. The negative tails decrease considerably with the averaging, and do not collapse with those of
$V=(16\varDelta _g)^3$. The negative tails decrease considerably with the averaging, and do not collapse with those of ![]() $\varSigma (10\varDelta _g)$, and
$\varSigma (10\varDelta _g)$, and ![]() $\varPsi (10\varDelta _g)$, while the positive tails are less affected. This asymmetry in the tails persists for large averaging volumes, as shown in figure 5(e, f), where we display the probability distribution of
$\varPsi (10\varDelta _g)$, while the positive tails are less affected. This asymmetry in the tails persists for large averaging volumes, as shown in figure 5(e, f), where we display the probability distribution of ![]() $\langle \varSigma \rangle _V$ and
$\langle \varSigma \rangle _V$ and ![]() $\langle \varPsi \rangle _V$ for a volume of the order of the integral scale of the flow,
$\langle \varPsi \rangle _V$ for a volume of the order of the integral scale of the flow, ![]() $V^{1/3}=1.2L_0=32\varDelta _g$. Neither of the two probability distributions are Gaussian, specially in its negative tails.
$V^{1/3}=1.2L_0=32\varDelta _g$. Neither of the two probability distributions are Gaussian, specially in its negative tails.
These results point to essential differences between inverse and direct energy transfer events, which seem to emerge from different dynamical processes. While direct energy fluxes are correlated with fluxes at larger scales, inverse energy fluxes are not, suggesting that local backscatter, measured as ![]() $\varSigma <0$ or
$\varSigma <0$ or ![]() $\varPsi <0$, does not necessarily imply a net inverse cascade of energy. This is corroborated by the strong depletion of inverse energy transfer events with volume averaging, which suggest that backscatter might be a consequence of space-local conservative fluxes, which cancel out when averaged, rather than of interscale interactions. Let us note that
$\varPsi <0$, does not necessarily imply a net inverse cascade of energy. This is corroborated by the strong depletion of inverse energy transfer events with volume averaging, which suggest that backscatter might be a consequence of space-local conservative fluxes, which cancel out when averaged, rather than of interscale interactions. Let us note that ![]() $\varSigma$ and
$\varSigma$ and ![]() $\varPsi$ differ in fact by a spatial flux, and that the intensity and probability of backscatter events are a specially noticeable difference between the two definitions. These space-local fluxes seem to cause a higher probability of backscatter in
$\varPsi$ differ in fact by a spatial flux, and that the intensity and probability of backscatter events are a specially noticeable difference between the two definitions. These space-local fluxes seem to cause a higher probability of backscatter in ![]() $\varPsi$ than in
$\varPsi$ than in ![]() $\varSigma$, suggesting that they are also, to some extent, the cause of backscatter in
$\varSigma$, suggesting that they are also, to some extent, the cause of backscatter in ![]() $\varSigma$. In view of these results, it is unlikely that the probability of inverse cascades can be quantified from the probability of local backscatter. Even if we could do so by analysing a massive database, and by devising a local definition of the energy transfer free of spatial fluxes, our results suggest that the energy cascade is sufficiently out of equilibrium for these predictions to have little practical importance.
$\varSigma$. In view of these results, it is unlikely that the probability of inverse cascades can be quantified from the probability of local backscatter. Even if we could do so by analysing a massive database, and by devising a local definition of the energy transfer free of spatial fluxes, our results suggest that the energy cascade is sufficiently out of equilibrium for these predictions to have little practical importance.
6. The structure of the inverse and direct cascades
The velocity gradients constitute a convenient descriptor of the fundamental structure of turbulent flows and some of their statistics reflect the out-of-equilibrium nature of turbulence. Although they describe only the structure of the small scales, the statistical distributions of the filtered velocity gradients are invariant across scales and reveal the self-similar structure of the inertial range (Borue & Orszag Reference Borue and Orszag1998; Lüthi et al. Reference Lüthi, Ott, Berg and Mann2007; Lozano-Durán et al. Reference Lozano-Durán, Holzner and Jiménez2016; Danish & Meneveau Reference Danish and Meneveau2018). Some investigations suggest a connection between the velocity gradients in the inertial scales and the energy cascade (Borue & Orszag Reference Borue and Orszag1998; Meneveau & Katz Reference Meneveau and Katz1999; Goto Reference Goto2008), and common SGS models rely on the assumption that energy transfer towards the unresolved scales can be reproduced using the velocity gradients of the resolved scales (Smagorinsky Reference Smagorinsky1963; Bardina et al. Reference Bardina, Ferziger and Reynolds1980; Nicoud & Ducros Reference Nicoud and Ducros1999). The structure of the velocity gradients is compactly represented by the invariants of the velocity gradient tensor. Supported on the space locality of the energy cascade reported in § 5.2, we will relate these invariants, which are strictly local in space, with local energy fluxes, connecting the energy cascade in physical space to the local structure of the flow.
6.1. Dynamics of the invariants of the velocity gradient tensor
Let ![]() $\mathcal {A}_{ij}=\partial _{j} u_i$ be the velocity gradient tensor of an incompressible flow. The second and third invariants of
$\mathcal {A}_{ij}=\partial _{j} u_i$ be the velocity gradient tensor of an incompressible flow. The second and third invariants of ![]() $\mathcal {A}_{ij}$ are
$\mathcal {A}_{ij}$ are
where ![]() $\omega _i$ is the
$\omega _i$ is the ![]() $i$-th component of the vorticity vector. Considering
$i$-th component of the vorticity vector. Considering ![]() $R$ and the discriminant
$R$ and the discriminant ![]() $D=27/4R^2+Q^3$, the flow can be classified in four different topological types: positive
$D=27/4R^2+Q^3$, the flow can be classified in four different topological types: positive ![]() $D$ corresponds to rotating topologies and negative
$D$ corresponds to rotating topologies and negative ![]() $D$ to saddle-node topologies; negative
$D$ to saddle-node topologies; negative ![]() $R$ accounts for topologies with a stretching principal direction and positive
$R$ accounts for topologies with a stretching principal direction and positive ![]() $R$ for topologies with a compressing principal direction. These invariants are also related to the vorticity vector and the rate-of-strain tensor, such that
$R$ for topologies with a compressing principal direction. These invariants are also related to the vorticity vector and the rate-of-strain tensor, such that ![]() $Q$ indicates the balance between enstrophy and strain, denoted by
$Q$ indicates the balance between enstrophy and strain, denoted by ![]() $|S|^2=2S_{ij}S_{ij}$ and
$|S|^2=2S_{ij}S_{ij}$ and ![]() $|\omega |^2=\omega _i\omega _i$, and
$|\omega |^2=\omega _i\omega _i$, and ![]() $R$ represents the balance between vortex stretching and strain self-amplification,
$R$ represents the balance between vortex stretching and strain self-amplification, ![]() $\omega _iS_{ij}\omega _j$ and
$\omega _iS_{ij}\omega _j$ and ![]() $S_{ij}S_{jk}S_{ki}$. These terms appear in the evolution equations of
$S_{ij}S_{jk}S_{ki}$. These terms appear in the evolution equations of ![]() $|S|^2$ and
$|S|^2$ and ![]() $|\omega |^2$,
$|\omega |^2$,
where ![]() $D_t=\partial _t+u_j\partial _j$ is the substantial derivative along a Lagrangian trajectory. Note that for simplicity we have considered the evolution of an inviscid flow for simplicity.
$D_t=\partial _t+u_j\partial _j$ is the substantial derivative along a Lagrangian trajectory. Note that for simplicity we have considered the evolution of an inviscid flow for simplicity.
The statistical distribution of ![]() $Q$ and
$Q$ and ![]() $R$ in turbulent flows has a typical teardrop shape, which is shown in figure 6(e). For ease of reference, we have divided the
$R$ in turbulent flows has a typical teardrop shape, which is shown in figure 6(e). For ease of reference, we have divided the ![]() $Q$–
$Q$–![]() $R$ plane into four quadrants, where
$R$ plane into four quadrants, where ![]() $q_1$ corresponds to
$q_1$ corresponds to ![]() $Q>0$ and
$Q>0$ and ![]() $R>0$,
$R>0$, ![]() $q_2$ to
$q_2$ to ![]() $Q>0$ and
$Q>0$ and ![]() $R<0$,
$R<0$, ![]() $q_3$ to
$q_3$ to ![]() $Q<0$ and
$Q<0$ and ![]() $R<0$, and
$R<0$, and ![]() $q_4$ to
$q_4$ to ![]() $Q<0$ and
$Q<0$ and ![]() $R>0$. The teardrop shape is characterised by a lobe in
$R>0$. The teardrop shape is characterised by a lobe in ![]() $q_2$, where the enstrophy is dominant over the strain and the vortex stretching over the strain self-amplification, and a tail in
$q_2$, where the enstrophy is dominant over the strain and the vortex stretching over the strain self-amplification, and a tail in ![]() $q_4$, which is known as the Vieillefosse (Reference Vieillefosse1984) tail, and represents dominant strain self-amplification over vortex stretching in strain-dominated regions. The high absolute values of
$q_4$, which is known as the Vieillefosse (Reference Vieillefosse1984) tail, and represents dominant strain self-amplification over vortex stretching in strain-dominated regions. The high absolute values of ![]() $Q$ in the Vieillefosse tail and in the upper semiplane indicate the spatial segregation of
$Q$ in the Vieillefosse tail and in the upper semiplane indicate the spatial segregation of ![]() $|S|$ and
$|S|$ and ![]() $|\omega |$. Low absolute values of
$|\omega |$. Low absolute values of ![]() $Q$ do not in general imply low values of
$Q$ do not in general imply low values of ![]() $|S|$ or
$|S|$ or ![]() $|\omega |$, but rather that
$|\omega |$, but rather that ![]() $|S|\sim |\omega |$. We actually find that
$|S|\sim |\omega |$. We actually find that ![]() $|S|\sim \langle |S| \rangle$ in regions where
$|S|\sim \langle |S| \rangle$ in regions where ![]() $Q\sim 0$ and
$Q\sim 0$ and ![]() $R\sim 0$. For a detailed interpretation of the
$R\sim 0$. For a detailed interpretation of the ![]() $Q$–
$Q$–![]() $R$ plane, we refer the reader to Tsinober (Reference Tsinober2000).
$R$ plane, we refer the reader to Tsinober (Reference Tsinober2000).

Figure 6. Line arrow, solid line, conditional mean trajectories in the ![]() $Q$–
$Q$–![]() $R$ plane for the inverse (a–d) and direct (e–h) evolutions due to different contributions. (i–l) Modulus of the probability transport velocities
$R$ plane for the inverse (a–d) and direct (e–h) evolutions due to different contributions. (i–l) Modulus of the probability transport velocities ![]() $|\boldsymbol {\varPhi }|$ in the
$|\boldsymbol {\varPhi }|$ in the ![]() $Q$–
$Q$–![]() $R$ plane in the direct evolution due to the different contributions. (a,e,i) All contributions
$R$ plane in the direct evolution due to the different contributions. (a,e,i) All contributions ![]() $\boldsymbol {\varPhi }_T$, (b, f, j) SGS model
$\boldsymbol {\varPhi }_T$, (b, f, j) SGS model ![]() $\boldsymbol {\varPhi }_M$, (c,g,k) restricted Euler
$\boldsymbol {\varPhi }_M$, (c,g,k) restricted Euler ![]() $\boldsymbol {\varPhi }_E$ and (d,h,l) non-local component of the pressure Hessian
$\boldsymbol {\varPhi }_E$ and (d,h,l) non-local component of the pressure Hessian ![]() $\boldsymbol {\varPhi }_P$. Contours of the probability density function of
$\boldsymbol {\varPhi }_P$. Contours of the probability density function of ![]() $Q$ and
$Q$ and ![]() $R$ contain 0.9 and 0.96 of the total data. All quantities are normalised using
$R$ contain 0.9 and 0.96 of the total data. All quantities are normalised using ![]() $t_Q={\langle Q^2 \rangle }^{1/4}$.
$t_Q={\langle Q^2 \rangle }^{1/4}$.
The dynamics of the velocity gradients can be statistically represented by the probability transport velocities in the ![]() $Q$–
$Q$–![]() $R$ plane, which are obtained from the average Lagrangian evolution of
$R$ plane, which are obtained from the average Lagrangian evolution of ![]() $Q$ and
$Q$ and ![]() $R$ (Ooi et al. Reference Ooi, Martín, Soria and Chong1999). Taking spatial derivatives in the evolution equations of the velocity field described by (3.6) and considering (6.1), (6.2), the Lagrangian evolution of the invariants reads as
$R$ (Ooi et al. Reference Ooi, Martín, Soria and Chong1999). Taking spatial derivatives in the evolution equations of the velocity field described by (3.6) and considering (6.1), (6.2), the Lagrangian evolution of the invariants reads as
where ![]() $\mathcal {H}_{ij}=\mathcal {H}^P_{ij}+\mathcal {H}^M_{ij}$ comprises the contribution of the non-local component of the pressure Hessian and the SGS model,
$\mathcal {H}_{ij}=\mathcal {H}^P_{ij}+\mathcal {H}^M_{ij}$ comprises the contribution of the non-local component of the pressure Hessian and the SGS model, ![]() $\mathcal {H}_{ij}^P={\partial _{ij} p -((\partial _{kk}p)\delta _{ij})/{3}}$ and
$\mathcal {H}_{ij}^P={\partial _{ij} p -((\partial _{kk}p)\delta _{ij})/{3}}$ and ![]() $\mathcal {H}_{ij}^M=\partial _j{M_i}$. Here,
$\mathcal {H}_{ij}^M=\partial _j{M_i}$. Here, ![]() $M_i$ is the
$M_i$ is the ![]() $i$-th component of the SGS model in the momentum equation and
$i$-th component of the SGS model in the momentum equation and ![]() $\delta _{ij}$ is the Kronecker's delta. The total probability transport velocity is defined as
$\delta _{ij}$ is the Kronecker's delta. The total probability transport velocity is defined as
where ![]() $\langle \cdot \rangle _C$ is the probability conditioned to
$\langle \cdot \rangle _C$ is the probability conditioned to ![]() $Q$ and
$Q$ and ![]() $R$, and
$R$, and ![]() $t_Q=1/\langle Q^2 \rangle ^{1/4}$ is a characteristic time extracted from the standard deviation of
$t_Q=1/\langle Q^2 \rangle ^{1/4}$ is a characteristic time extracted from the standard deviation of ![]() $Q$. Let us note that the probability density flux in the
$Q$. Let us note that the probability density flux in the ![]() $Q$–
$Q$–![]() $R$ plane is
$R$ plane is ![]() $P(Q,R)\boldsymbol {\varPhi }_T$, where
$P(Q,R)\boldsymbol {\varPhi }_T$, where ![]() $P(Q,R)$ is the joint probability density of
$P(Q,R)$ is the joint probability density of ![]() $Q$ and
$Q$ and ![]() $R$. The probability transport velocities are integrated to yield conditional mean trajectories (CMTs) in the
$R$. The probability transport velocities are integrated to yield conditional mean trajectories (CMTs) in the ![]() $Q$–
$Q$–![]() $R$ plane (Ooi et al. Reference Ooi, Martín, Soria and Chong1999), which are shown also in figure 6(e).
$R$ plane (Ooi et al. Reference Ooi, Martín, Soria and Chong1999), which are shown also in figure 6(e).
To analyse the dynamics of the invariants, we decompose the CMTs into the contribution of the different terms in the evolution equation of ![]() $Q$ and
$Q$ and ![]() $R$,
$R$,
where ![]() $\boldsymbol {\varPhi }_T=\boldsymbol {\varPhi }_E+\boldsymbol {\varPhi }_P+\boldsymbol {\varPhi }_M$, and the normalisation with
$\boldsymbol {\varPhi }_T=\boldsymbol {\varPhi }_E+\boldsymbol {\varPhi }_P+\boldsymbol {\varPhi }_M$, and the normalisation with ![]() $t_Q$ has been dropped for simplicity. This decomposition separates the strictly space-local dynamics of restricted Euler (RE) (Cantwell Reference Cantwell1992),
$t_Q$ has been dropped for simplicity. This decomposition separates the strictly space-local dynamics of restricted Euler (RE) (Cantwell Reference Cantwell1992), ![]() $\boldsymbol {\varPhi }_E$, which depends exclusively on
$\boldsymbol {\varPhi }_E$, which depends exclusively on ![]() $Q$ and
$Q$ and ![]() $R$, and includes advection and the local action of the pressure Hessian, from the non-local action of the pressure Hessian and the SGS model, which are included in
$R$, and includes advection and the local action of the pressure Hessian, from the non-local action of the pressure Hessian and the SGS model, which are included in ![]() $\boldsymbol {\varPhi }_P$ and
$\boldsymbol {\varPhi }_P$ and ![]() $\boldsymbol {\varPhi }_M$, respectively. This separation into local and non-local dynamics is convenient to justify the prevalence of direct over inverse cascades. In order to compare the importance of the different terms, we consider the norm of the probability transport velocities,
$\boldsymbol {\varPhi }_M$, respectively. This separation into local and non-local dynamics is convenient to justify the prevalence of direct over inverse cascades. In order to compare the importance of the different terms, we consider the norm of the probability transport velocities,
Statistics of ![]() $Q$ and
$Q$ and ![]() $R$ and their CMTs have been compiled for two different times in the ensemble of realisations,
$R$ and their CMTs have been compiled for two different times in the ensemble of realisations, ![]() $t_{stats}=(1 \pm 0.12)t_{inv}$, which correspond to the direct and inverse evolutions and are marked in figure 1(a). If we assume that the decay of the system is self-similar, conclusions drawn from this analysis should be independent of
$t_{stats}=(1 \pm 0.12)t_{inv}$, which correspond to the direct and inverse evolutions and are marked in figure 1(a). If we assume that the decay of the system is self-similar, conclusions drawn from this analysis should be independent of ![]() $t_{stats}$. The total probability transport velocity,
$t_{stats}$. The total probability transport velocity, ![]() $\boldsymbol {\varPhi }_T$, has been calculated directly from the expression of the substantial derivative, computing separately the temporal and convective derivatives. Appropriate numerical methods have been used in all the computations (Lozano-Durán, Holzner & Jiménez Reference Lozano-Durán, Holzner and Jiménez2015). Results show that the number of realisations in our database is sufficient to converge the statistics.
$\boldsymbol {\varPhi }_T$, has been calculated directly from the expression of the substantial derivative, computing separately the temporal and convective derivatives. Appropriate numerical methods have been used in all the computations (Lozano-Durán, Holzner & Jiménez Reference Lozano-Durán, Holzner and Jiménez2015). Results show that the number of realisations in our database is sufficient to converge the statistics.
The different contributions to the CMTs and the norm of the probability transport velocities in the inverse and direct evolutions are shown in figures 6(a–h) and 6(i–l). In the direct evolution, the CMTs develop an average rotating cycle characteristic of turbulent flows, which exposes causality between the different configurations of the flow in an average sense. The CMTs rotate clockwise: from dominant vortex stretching to dominant vortex compression in the upper semiplane, to the Vieillefosse tail in ![]() $q_4$, and again to dominant vortex stretching in enstrophy-dominated regions.
$q_4$, and again to dominant vortex stretching in enstrophy-dominated regions.
The CMTs move from negative to positive ![]() $R$, and finally to the Vieillefosse tail, due to the effect of the RE dynamics. This trend would cause the appearance of infinite gradients in a finite time (Vieillefosse Reference Vieillefosse1984), but the non-local effect of the pressure Hessian and the SGS model, or viscosity in the case of direct numerical simulations, prevent it by bringing the CMTs back to
$R$, and finally to the Vieillefosse tail, due to the effect of the RE dynamics. This trend would cause the appearance of infinite gradients in a finite time (Vieillefosse Reference Vieillefosse1984), but the non-local effect of the pressure Hessian and the SGS model, or viscosity in the case of direct numerical simulations, prevent it by bringing the CMTs back to ![]() $q_3$ and restarting the cycle. For closed steady states, CMTs describe a closed cycle (Lozano-Durán et al. Reference Lozano-Durán, Holzner and Jiménez2016), while in our decaying flow they spiral inwards due to the action the SGS model, which contracts the probability distribution, resembling the action of the viscosity in direct numerical simulations (Meneveau Reference Meneveau2011). The CMTs of the non-local component of the pressure Hessian evolve from positive to negative values of
$q_3$ and restarting the cycle. For closed steady states, CMTs describe a closed cycle (Lozano-Durán et al. Reference Lozano-Durán, Holzner and Jiménez2016), while in our decaying flow they spiral inwards due to the action the SGS model, which contracts the probability distribution, resembling the action of the viscosity in direct numerical simulations (Meneveau Reference Meneveau2011). The CMTs of the non-local component of the pressure Hessian evolve from positive to negative values of ![]() $R$, following the same behaviour observed by Chevillard et al. (Reference Chevillard, Meneveau, Biferale and Toschi2008) and Meneveau (Reference Meneveau2011). The norm of the probability transport velocities reveals that the RE dynamics is mostly counteracted by the non-local component of the pressure Hessian in regions where
$R$, following the same behaviour observed by Chevillard et al. (Reference Chevillard, Meneveau, Biferale and Toschi2008) and Meneveau (Reference Meneveau2011). The norm of the probability transport velocities reveals that the RE dynamics is mostly counteracted by the non-local component of the pressure Hessian in regions where ![]() $Q$ and
$Q$ and ![]() $R$ are large. These observations are in agreement with Lüthi, Holzner & Tsinober (Reference Lüthi, Holzner and Tsinober2009), and evidence a secondary role of the model in the dynamics of intense gradients.
$R$ are large. These observations are in agreement with Lüthi, Holzner & Tsinober (Reference Lüthi, Holzner and Tsinober2009), and evidence a secondary role of the model in the dynamics of intense gradients.
In the inverse evolution we identify substantial changes. As explained in § 4, time reversal changes only the sign of quantities which are odd with the velocity: ![]() $Q$ remains unaltered while
$Q$ remains unaltered while ![]() $R$ changes sign, leading to an inverse teardrop shape. The Vieillefosse tail lies now in
$R$ changes sign, leading to an inverse teardrop shape. The Vieillefosse tail lies now in ![]() $q_3$, forming an antitail, and a higher probability of vortex compression appears in enstrophy-dominated regions. This transformation also affects the CMTs, and is most relevant in the effect of the SGS model, which now expands the probability distribution and leads to an average outward spiralling. The behaviour of
$q_3$, forming an antitail, and a higher probability of vortex compression appears in enstrophy-dominated regions. This transformation also affects the CMTs, and is most relevant in the effect of the SGS model, which now expands the probability distribution and leads to an average outward spiralling. The behaviour of ![]() $\boldsymbol {\varPhi }_E$ and
$\boldsymbol {\varPhi }_E$ and ![]() $\boldsymbol {\varPhi }_P$ is similar to the direct evolution in the upper semiplane, but undergoes fundamental changes in the lower semiplane. In the direct evolution the non-local component of the pressure Hessian counteracts the RE dynamics, preventing the formation of intense gradients in the Vieillefosse tail. Conversely, in the inverse evolution,
$\boldsymbol {\varPhi }_P$ is similar to the direct evolution in the upper semiplane, but undergoes fundamental changes in the lower semiplane. In the direct evolution the non-local component of the pressure Hessian counteracts the RE dynamics, preventing the formation of intense gradients in the Vieillefosse tail. Conversely, in the inverse evolution, ![]() $\boldsymbol {\varPhi }_P$ favours the growth of intense gradients in the antitail, while the RE opposes it.
$\boldsymbol {\varPhi }_P$ favours the growth of intense gradients in the antitail, while the RE opposes it.
This analysis compares the structure of the ‘attractor’ with that of the ‘antiattractor’, and can be simply derived by considering the effect that the transformation ![]() $\boldsymbol {u}\rightarrow - \boldsymbol {u}$ has on the dynamics of the velocity gradients. However, we have identified in § 5.1 inverse trajectories outside the antiattractor. We will show that, for these trajectories, this analysis yields non-trivial results.
$\boldsymbol {u}\rightarrow - \boldsymbol {u}$ has on the dynamics of the velocity gradients. However, we have identified in § 5.1 inverse trajectories outside the antiattractor. We will show that, for these trajectories, this analysis yields non-trivial results.
6.2. Asymmetry in the  $Q$–
$Q$– $R$ space
$R$ space
The statistical irreversibility of the cascade is clearly manifest in the statistics of the invariants through the asymmetry of the probability distribution with respect to ![]() $R=0$. To characterise statistical irreversibility in the
$R=0$. To characterise statistical irreversibility in the ![]() $Q$–
$Q$–![]() $R$ plane, we use an asymmetry function
$R$ plane, we use an asymmetry function
where ![]() $P^+$ and
$P^+$ and ![]() $P^-$ denote the probability density of
$P^-$ denote the probability density of ![]() $Q$ and
$Q$ and ![]() $R$ in the direct and inverse evolutions, respectively. Figure 7(a) shows the distribution of
$R$ in the direct and inverse evolutions, respectively. Figure 7(a) shows the distribution of ![]() $\varpi (Q,R)$, while 7(b) shows the absolute values of the asymmetry function averaged along the
$\varpi (Q,R)$, while 7(b) shows the absolute values of the asymmetry function averaged along the ![]() $R$ axis,
$R$ axis,
 \begin{equation} \langle\varpi(Q)\rangle_R=\frac{\displaystyle\int|\varpi(Q,R)|{\,\textrm{{d}}}{R}}{\displaystyle\int {\,\textrm{{d}}} R}. \end{equation}
\begin{equation} \langle\varpi(Q)\rangle_R=\frac{\displaystyle\int|\varpi(Q,R)|{\,\textrm{{d}}}{R}}{\displaystyle\int {\,\textrm{{d}}} R}. \end{equation}
Most of the temporal asymmetry of the velocity gradients is related to ![]() $Q<0$, where the strain is dominant over the vorticity. In enstrophy-dominated regions vortex stretching is on average dominant in the direct evolution, but the probability of vortex compression is not negligible. Both processes also occur in the inverse cascade, in which vortex compression is more probable but coexists with vortex stretching. On the other hand, the structure of strain-dominated regions depends strongly on the direction of the system in time. Intense velocity gradients in
$Q<0$, where the strain is dominant over the vorticity. In enstrophy-dominated regions vortex stretching is on average dominant in the direct evolution, but the probability of vortex compression is not negligible. Both processes also occur in the inverse cascade, in which vortex compression is more probable but coexists with vortex stretching. On the other hand, the structure of strain-dominated regions depends strongly on the direction of the system in time. Intense velocity gradients in ![]() $Q<0$ are either in
$Q<0$ are either in ![]() $q_3$ or
$q_3$ or ![]() $q_4$, depending on the direction of the cascade, but not simultaneously in both quadrants. The dynamics of strain-dominated regions are more fundamentally related to the direction of the system in time than the dynamics of enstrophy-dominated regions.
$q_4$, depending on the direction of the cascade, but not simultaneously in both quadrants. The dynamics of strain-dominated regions are more fundamentally related to the direction of the system in time than the dynamics of enstrophy-dominated regions.

Figure 7. (a) Colour plot of the asymmetry function ![]() $\varpi (Q,R)$. Isocontours contain
$\varpi (Q,R)$. Isocontours contain ![]() $0.7$ and
$0.7$ and ![]() $0.85$ of the total data. Dashed lines represent the contours of the asymmetry function when
$0.85$ of the total data. Dashed lines represent the contours of the asymmetry function when ![]() $R\rightarrow -R$. (b) Asymmetry function averaged along the
$R\rightarrow -R$. (b) Asymmetry function averaged along the ![]() $R$ axis,
$R$ axis, ![]() $\langle \varpi (Q)\rangle _R$, for
$\langle \varpi (Q)\rangle _R$, for ![]() $R$ in the interval
$R$ in the interval ![]() $(-2,2)$. Quantities are normalised using
$(-2,2)$. Quantities are normalised using ![]() $t_Q={\langle Q^2 \rangle }^{1/4}$.
$t_Q={\langle Q^2 \rangle }^{1/4}$.
6.3. Energy fluxes in the  $Q$–
$Q$– $R$ plane: inverse evolutions outside the ‘antiattractor’
$R$ plane: inverse evolutions outside the ‘antiattractor’
We now analyse the relation between the local structure of the flow and the energy cascade by conditioning the statistics of the local energy fluxes to the invariants of the filtered velocity gradients. First, we study the experiments on the inverse cascade without the model, which are presented in § 4.3. These experiments provide non-trivial inverse evolutions outside the ‘antiattractor’, for which this analysis identifies the structures that support the inverse energy cascade.
We calculate the invariants of the filtered velocity gradients and their CMTs at scale ![]() $\check {\varDelta }=5\varDelta _g$. We use a Gaussian filter (4.1), and calculate the CMTs using the substantial derivative of the filtered field,
$\check {\varDelta }=5\varDelta _g$. We use a Gaussian filter (4.1), and calculate the CMTs using the substantial derivative of the filtered field, ![]() $\check {D}_t=\partial _t+\check {u}_i\partial _i$. We analyse these quantities in the inverse evolutions when the model is removed, and connect them to the evolution of the local energy fluxes in physical space,
$\check {D}_t=\partial _t+\check {u}_i\partial _i$. We analyse these quantities in the inverse evolutions when the model is removed, and connect them to the evolution of the local energy fluxes in physical space, ![]() $\varSigma (\boldsymbol {x},t)$, and in scale space,
$\varSigma (\boldsymbol {x},t)$, and in scale space, ![]() $\varPi (k,t)$. The analysis of
$\varPi (k,t)$. The analysis of ![]() $\varPsi$ yields qualitatively similar results.
$\varPsi$ yields qualitatively similar results.
Figure 8(a–h) show the probability distribution of the invariants of the unfiltered (a–d), and filtered (e–h) velocity gradients, and the their CMTs, in the inverse evolution without the model. Figure 8(i–l) show the averaged ![]() $\varSigma (5\varDelta _g)$ conditioned to the invariants of the filtered velocity gradients.
$\varSigma (5\varDelta _g)$ conditioned to the invariants of the filtered velocity gradients.

Figure 8. Conditional mean trajectories in the ![]() $Q$–
$Q$–![]() $R$ plane of the inverse evolution without the model (see § 4.3) for (a–d) the unfiltered case and (e–h) filtered at
$R$ plane of the inverse evolution without the model (see § 4.3) for (a–d) the unfiltered case and (e–h) filtered at ![]() $\check {\varDelta }=5\varDelta _g$, and (i–l) conditional average of
$\check {\varDelta }=5\varDelta _g$, and (i–l) conditional average of ![]() $\varSigma$ at scale
$\varSigma$ at scale ![]() $\check {\varDelta }=5\varDelta _g$, at different times: (a,e)
$\check {\varDelta }=5\varDelta _g$, at different times: (a,e) ![]() $t/T_0=0$; (b, f)
$t/T_0=0$; (b, f) ![]() $t/T_0=0.1$; (c,g)
$t/T_0=0.1$; (c,g) ![]() $t/T_0=0.15$; (d,h)
$t/T_0=0.15$; (d,h) ![]() $t/T_0=0.25$. ——, solid magenta line, contours of the probability density function of
$t/T_0=0.25$. ——, solid magenta line, contours of the probability density function of ![]() $Q$ and
$Q$ and ![]() $R$ containing
$R$ containing ![]() $0.8$ and
$0.8$ and ![]() $0.9$ of the data. Here
$0.9$ of the data. Here ![]() $Q$ and
$Q$ and ![]() $R$ are normalised with
$R$ are normalised with ![]() $t_Q=\langle Q(t_{inv})^2\rangle ^{1/4}$. Conditional-averaged energy fluxes in (i–l) are normalised with the absolute value of
$t_Q=\langle Q(t_{inv})^2\rangle ^{1/4}$. Conditional-averaged energy fluxes in (i–l) are normalised with the absolute value of ![]() $\langle \varSigma \rangle$ at each time.
$\langle \varSigma \rangle$ at each time.
Initially, the statistics of the filtered and unfiltered velocity gradients are similar, and resemble those of the inverse evolutions. The average ![]() $\varSigma$ conditioned to
$\varSigma$ conditioned to ![]() $Q$ and
$Q$ and ![]() $R$ is predominantly negative and most intense in
$R$ is predominantly negative and most intense in ![]() $q_3$ and
$q_3$ and ![]() $q_1$, suggesting a relevant role of the antitail and of vortex compression in the inverse cascade.
$q_1$, suggesting a relevant role of the antitail and of vortex compression in the inverse cascade.
At time ![]() $0.1T_0$ after the inversion, the antitail of the unfiltered gradients has contracted, while the antitail of the filtered gradients remains unaltered. We do not yet see changes in the upper semiplane, where the probability distribution remains similar to the initial state in both cases. According to
$0.1T_0$ after the inversion, the antitail of the unfiltered gradients has contracted, while the antitail of the filtered gradients remains unaltered. We do not yet see changes in the upper semiplane, where the probability distribution remains similar to the initial state in both cases. According to ![]() $\varPi (k,t)$ in figure 2(a), at this time the direct cascade has not yet regenerated at the small scales. At the filter scale,
$\varPi (k,t)$ in figure 2(a), at this time the direct cascade has not yet regenerated at the small scales. At the filter scale, ![]() $\varPi (k,t)$ and
$\varPi (k,t)$ and ![]() $\langle \varSigma \rangle$ are still negative, and have a similar magnitude to the initial state.
$\langle \varSigma \rangle$ are still negative, and have a similar magnitude to the initial state.
At ![]() $0.15T_0$, the unfiltered velocity gradients start developing dominant vortex stretching, represented by a prominent lobe in
$0.15T_0$, the unfiltered velocity gradients start developing dominant vortex stretching, represented by a prominent lobe in ![]() $q_2$, and a regular Vieillefosse tail. The antitail, although reduced, is still observable in the filtered gradients and
$q_2$, and a regular Vieillefosse tail. The antitail, although reduced, is still observable in the filtered gradients and ![]() $\langle \varSigma \rangle <0$. At this stage, as shown in figure 2(a), an inverse cascade at the filter scale, and a direct cascade in the small scales coexist. Finally, at
$\langle \varSigma \rangle <0$. At this stage, as shown in figure 2(a), an inverse cascade at the filter scale, and a direct cascade in the small scales coexist. Finally, at ![]() $0.25T_0$, when the filtered velocity gradients develop structures in the Vieillefosse tail, the direct cascade regenerates at the filter scale and
$0.25T_0$, when the filtered velocity gradients develop structures in the Vieillefosse tail, the direct cascade regenerates at the filter scale and ![]() $\langle \varSigma \rangle >0$.
$\langle \varSigma \rangle >0$.
These results indicate a strong connection between the direction of the cascade and the orientation of the Vieillefosse tail. First, the conditional averages of ![]() $\varSigma$ in the
$\varSigma$ in the ![]() $Q$–
$Q$–![]() $R$ plane show that, at
$R$ plane show that, at ![]() $0.25T_0$, when the energy cascade starts to regenerate at the filter scale, direct local energy fluxes are most intense in the
$0.25T_0$, when the energy cascade starts to regenerate at the filter scale, direct local energy fluxes are most intense in the ![]() $q_4$ quadrant. Second, the differences in the invariants of the filtered velocity gradients between
$q_4$ quadrant. Second, the differences in the invariants of the filtered velocity gradients between ![]() $0.1T_0$ and
$0.1T_0$ and ![]() $0.15T_0$ are only significant in the Vieillefosse tail, but the inverse energy fluxes are reduced by a half,
$0.15T_0$ are only significant in the Vieillefosse tail, but the inverse energy fluxes are reduced by a half, ![]() $\langle \varSigma (0.15T_0)\rangle \simeq 0.5\langle \varSigma (0.1T_0)\rangle$.
$\langle \varSigma (0.15T_0)\rangle \simeq 0.5\langle \varSigma (0.1T_0)\rangle$.
The symmetry in the statistics of enstrophy-dominated regions reported in § 6.2 also holds during the transition from inverse to direct phase-space trajectories. At the filter scale, the probability distribution or the CMTs in the upper semiplane do not substantially change during the regeneration of the energy cascade.
6.4. Energy fluxes in the  $Q$–
$Q$– $R$ plane: direct evolutions in the turbulent ‘attractor’
$R$ plane: direct evolutions in the turbulent ‘attractor’
We perform the same analysis for the direct evolutions with the SGS model. Figure 9(a) shows the average ![]() $\varSigma$ conditioned to
$\varSigma$ conditioned to ![]() $Q$ and
$Q$ and ![]() $R$. To discriminate between direct and inverse energy transfer, we condition the probability distribution of
$R$. To discriminate between direct and inverse energy transfer, we condition the probability distribution of ![]() $Q$ and
$Q$ and ![]() $R$ to the sign of the local energy fluxes, and present the results in figure 9(b,c). We quantify in table 3 the relevance of each quadrant to the energy cascade by calculating the average of
$R$ to the sign of the local energy fluxes, and present the results in figure 9(b,c). We quantify in table 3 the relevance of each quadrant to the energy cascade by calculating the average of ![]() $\varSigma$ conditioned to
$\varSigma$ conditioned to ![]() $Q$ and
$Q$ and ![]() $R$ belonging to a quadrant,
$R$ belonging to a quadrant, ![]() $\langle \varSigma \rangle _{q_i}=\langle \varSigma |(Q,R)\in q_i\rangle$, and the total contribution of each quadrant to the energy fluxes,
$\langle \varSigma \rangle _{q_i}=\langle \varSigma |(Q,R)\in q_i\rangle$, and the total contribution of each quadrant to the energy fluxes, ![]() $\{\varSigma \}_{q_i}=\langle \varSigma \rangle _{q_i}P_{q_i}$, where
$\{\varSigma \}_{q_i}=\langle \varSigma \rangle _{q_i}P_{q_i}$, where ![]() $P_{q_i}$ is the probability that
$P_{q_i}$ is the probability that ![]() $Q$ and
$Q$ and ![]() $R$ belong to
$R$ belong to ![]() $q_i$, so that
$q_i$, so that ![]() $\langle \varSigma \rangle =\sum _{i=1,4}\{\varSigma \}_{q_i}$. We have also calculated these quantities conditioning the averages to the direction of the energy fluxes, being
$\langle \varSigma \rangle =\sum _{i=1,4}\{\varSigma \}_{q_i}$. We have also calculated these quantities conditioning the averages to the direction of the energy fluxes, being
the average energy transfer conditioned to the quadrant ![]() $q_i$ and to
$q_i$ and to ![]() $\varSigma >0$. Accordingly,
$\varSigma >0$. Accordingly, ![]() $\{\varSigma \}^+_{q_i}=\langle \varSigma \rangle ^+_{q_i}P^+_{q_i}$ is the total contribution of the quadrant
$\{\varSigma \}^+_{q_i}=\langle \varSigma \rangle ^+_{q_i}P^+_{q_i}$ is the total contribution of the quadrant ![]() $q_i$ to the positive energy fluxes. Here
$q_i$ to the positive energy fluxes. Here ![]() $P^+_{q_i}$ is the probability that
$P^+_{q_i}$ is the probability that ![]() $Q$ and
$Q$ and ![]() $R$ belongs to
$R$ belongs to ![]() $q_i$ and that
$q_i$ and that ![]() $\varSigma >0$. Statistics conditioned to negative fluxes are marked with a minus superscript.
$\varSigma >0$. Statistics conditioned to negative fluxes are marked with a minus superscript.

Figure 9. (a) Conditional average of ![]() $\varSigma$ at scale
$\varSigma$ at scale ![]() $\check {\varDelta }=5\varDelta _g$ in the
$\check {\varDelta }=5\varDelta _g$ in the ![]() $Q$–
$Q$–![]() $R$ plane of the filtered velocity gradients for the direct evolution with the model. (b) Average
$R$ plane of the filtered velocity gradients for the direct evolution with the model. (b) Average ![]() $\varSigma$ over
$\varSigma$ over ![]() $Q$ and
$Q$ and ![]() $R$ conditioned to
$R$ conditioned to ![]() $\varSigma >0$. (c) Absolute value of the average
$\varSigma >0$. (c) Absolute value of the average ![]() $\varSigma$ over
$\varSigma$ over ![]() $Q$ and
$Q$ and ![]() $R$ conditioned to
$R$ conditioned to ![]() $\varSigma <0$. Values of
$\varSigma <0$. Values of ![]() $\varSigma$ normalised with
$\varSigma$ normalised with ![]() $\langle \varSigma \rangle$ at
$\langle \varSigma \rangle$ at ![]() $t_{stats}$. ——, solid magenta line, contours of the probability density function of
$t_{stats}$. ——, solid magenta line, contours of the probability density function of ![]() $Q$ and
$Q$ and ![]() $R$ containing
$R$ containing ![]() $0.85$ and
$0.85$ and ![]() $0.9$ of the data. In (c),
$0.9$ of the data. In (c), ![]() $-\cdot -$ marks isocontours of
$-\cdot -$ marks isocontours of ![]() $Q$ and
$Q$ and ![]() $R$ conditioned to negative
$R$ conditioned to negative ![]() $\varSigma$ for the inverse evolutions. The dashed line corresponds to
$\varSigma$ for the inverse evolutions. The dashed line corresponds to ![]() $D=0$. Here
$D=0$. Here ![]() $Q$ and
$Q$ and ![]() $R$ are normalised with
$R$ are normalised with ![]() $t_Q={\langle Q^2 \rangle }^{1/4}$.
$t_Q={\langle Q^2 \rangle }^{1/4}$.
Table 3. Conditional averages of energy transfer and contributions to the total energy fluxes of each quadrant in the ![]() $Q$–
$Q$–![]() $R$ plane during the direct evolution. In the first table we have considered all data, in the second only direct energy transfer events, and in the last only backscatter events. Quantities are normalised with the average
$R$ plane during the direct evolution. In the first table we have considered all data, in the second only direct energy transfer events, and in the last only backscatter events. Quantities are normalised with the average ![]() $\varSigma$ in the first case, and with the averages conditioned to positive and negative fluxes in the other two cases.
$\varSigma$ in the first case, and with the averages conditioned to positive and negative fluxes in the other two cases.

The most intense direct energy transfer events are related to structures in the Vieillefosse tail, and ![]() $q_4$ has the highest average energy transfer,
$q_4$ has the highest average energy transfer, ![]() $\langle \varSigma \rangle _{q_4}\sim 1.5\langle \varSigma \rangle$, and contributes with approximately
$\langle \varSigma \rangle _{q_4}\sim 1.5\langle \varSigma \rangle$, and contributes with approximately ![]() $50\,\%$ of the total energy transfer. Also structures in
$50\,\%$ of the total energy transfer. Also structures in ![]() $q_2$ are relevant to the cascade, with a contribution of around
$q_2$ are relevant to the cascade, with a contribution of around ![]() $30\,\%$ to the total fluxes. Conversely, the contribution of
$30\,\%$ to the total fluxes. Conversely, the contribution of ![]() $q_1$ to direct energy transfer is negligible. When we condition these statistics to direct energy fluxes, we obtain qualitatively similar results. The statistics of
$q_1$ to direct energy transfer is negligible. When we condition these statistics to direct energy fluxes, we obtain qualitatively similar results. The statistics of ![]() $Q$ and
$Q$ and ![]() $R$ conditioned to positive
$R$ conditioned to positive ![]() $\varSigma$ yield almost a complete teardrop, except for a lower probability of events in
$\varSigma$ yield almost a complete teardrop, except for a lower probability of events in ![]() $q_1$.
$q_1$.
When we condition to negative energy transfer events, the average inverse energy transfer is roughly similar in the four quadrants, but the ![]() $q_1$ quadrant contributes the most to the total, with a
$q_1$ quadrant contributes the most to the total, with a ![]() $56\,\%$. This is a consequence of inverse energy transfer events being mostly located in
$56\,\%$. This is a consequence of inverse energy transfer events being mostly located in ![]() $q_1$. As shown in figure 9(c), the statistics of
$q_1$. As shown in figure 9(c), the statistics of ![]() $Q$–
$Q$–![]() $R$ conditioned to inverse energy transfer resemble an inverse teardrop without the antitail. In the same figure we have plotted the probability density function of
$R$ conditioned to inverse energy transfer resemble an inverse teardrop without the antitail. In the same figure we have plotted the probability density function of ![]() $Q$ and
$Q$ and ![]() $R$ conditioned to inverse energy transfer in the inverse evolutions. By time symmetry, the antitail in
$R$ conditioned to inverse energy transfer in the inverse evolutions. By time symmetry, the antitail in ![]() $q_3$ contributes the most to inverse energy transfer in the inverse cascade, but this tail is absent in the direct evolution.
$q_3$ contributes the most to inverse energy transfer in the inverse cascade, but this tail is absent in the direct evolution.
6.5. An entropic argument for the prevalence of direct energy fluxes
We have presented in the previous section compelling evidence that topologies in the antitail are strongly connected to the inverse cascade, but that these topologies have negligible probability in the direct cascade. Here we provide arguments that explain the low probability of these topologies, and, consequently, of inverse cascades.
Consider the evolution of ![]() $R$ in regions where the strain is dominant over the enstrophy,
$R$ in regions where the strain is dominant over the enstrophy, ![]() $|S|^2\sim \langle |S|^2\rangle \gg |\omega |^2$. Neglecting the contribution of the enstrophy, we obtain
$|S|^2\sim \langle |S|^2\rangle \gg |\omega |^2$. Neglecting the contribution of the enstrophy, we obtain
where ![]() $\alpha _1\leqslant \alpha _2\leqslant \alpha _3$ are the eigenvalues of the rate-of-strain tensor. This is a good approximation to the Vieillefosse tail and the antitail, where
$\alpha _1\leqslant \alpha _2\leqslant \alpha _3$ are the eigenvalues of the rate-of-strain tensor. This is a good approximation to the Vieillefosse tail and the antitail, where ![]() $|S|^2\sim 100|\omega |^2$. Due to compressibility
$|S|^2\sim 100|\omega |^2$. Due to compressibility ![]() $\alpha _1 + \alpha _2 + \alpha _3=0$, and the sign of
$\alpha _1 + \alpha _2 + \alpha _3=0$, and the sign of ![]() $R$ is determined by the sign of the intermediate eigenvalue. Topologies in the Vieillefosse tail are characterised by
$R$ is determined by the sign of the intermediate eigenvalue. Topologies in the Vieillefosse tail are characterised by ![]() $\alpha _2>0$, while in the antitail
$\alpha _2>0$, while in the antitail ![]() $\alpha _2<0$. We describe the evolution of
$\alpha _2<0$. We describe the evolution of ![]() $R$ in terms of the evolution of
$R$ in terms of the evolution of ![]() $\alpha _2$, whose equation reads as
$\alpha _2$, whose equation reads as
where ![]() $\varLambda =\partial _{kk}p\approx -(|S|^2)/{2}=-\alpha ^2_1-\alpha ^2_2-\alpha ^2_3$ is the trace of the pressure Hessian, which is local, and
$\varLambda =\partial _{kk}p\approx -(|S|^2)/{2}=-\alpha ^2_1-\alpha ^2_2-\alpha ^2_3$ is the trace of the pressure Hessian, which is local, and ![]() $\varGamma _2$ is the contribution of
$\varGamma _2$ is the contribution of ![]() $\mathcal {H}^P_{ij}=\partial _{ij} p-(\partial _{kk}p\delta _{ij})/{3}$ to the evolution of
$\mathcal {H}^P_{ij}=\partial _{ij} p-(\partial _{kk}p\delta _{ij})/{3}$ to the evolution of ![]() $\alpha _2$, which is non-local. We have discarded quadratic terms in the vorticity and the action of the SGS model, which we show above to have a negligible contribution to the dynamics of intense gradients (Nomura & Post Reference Nomura and Post1998). Disregarding the action of the non-local component of the pressure Hessian,
$\alpha _2$, which is non-local. We have discarded quadratic terms in the vorticity and the action of the SGS model, which we show above to have a negligible contribution to the dynamics of intense gradients (Nomura & Post Reference Nomura and Post1998). Disregarding the action of the non-local component of the pressure Hessian, ![]() $\varGamma _2$, the equation reads as
$\varGamma _2$, the equation reads as
where we have used the fact that, from their definition, ![]() $\alpha _1^2>\alpha _2^2$ and
$\alpha _1^2>\alpha _2^2$ and ![]() $\alpha _3^2>\alpha _2^2$. The evolution of any initial value of
$\alpha _3^2>\alpha _2^2$. The evolution of any initial value of ![]() $\alpha _2$ results in the growth of the intermediate eigenvalue, leading to positive values of
$\alpha _2$ results in the growth of the intermediate eigenvalue, leading to positive values of ![]() $R$. This is the effect of the RE dynamics, which depletes the antitail in the direct cascade. Left to itself, it generates intense strain in the Vieillefosse tail, and is independent on the non-local structure of the velocity gradients. From (6.17) we conclude that the only inertial mechanism capable of preventing the rate-of-strain tensor from developing a positive intermediate eigenvalue is the non-local action of the pressure Hessian through
$R$. This is the effect of the RE dynamics, which depletes the antitail in the direct cascade. Left to itself, it generates intense strain in the Vieillefosse tail, and is independent on the non-local structure of the velocity gradients. From (6.17) we conclude that the only inertial mechanism capable of preventing the rate-of-strain tensor from developing a positive intermediate eigenvalue is the non-local action of the pressure Hessian through ![]() $\varGamma _2$. This analysis is consistent with the results presented in § 6.1, where we show that this term sustains the antitail in the inverse cascade.
$\varGamma _2$. This analysis is consistent with the results presented in § 6.1, where we show that this term sustains the antitail in the inverse cascade.
The non-local pressure Hessian depends on the complete flow field. In the absence of boundaries it can be expressed as a singular integral, which depends on all the points of the domain (Speziale, Sarkar & Gatski Reference Speziale, Sarkar and Gatski1991; Ohkitani & Kishiba Reference Ohkitani and Kishiba1995). As a consequence, the non-local pressure Hessian is in general decorrelated from the local dynamics of the velocity gradients (She et al. Reference She, Jackson, Orszag, Hunt, Phillips and Williams1991). Figure 10(a) shows the joint probability distribution of the two components of ![]() $\boldsymbol {\varPhi }_P=\{\mathcal {A}_{ij}\mathcal {H}^P_{ji},-\mathcal {A}_{ij}\mathcal {A}_{jk}\mathcal {H}^P_{ki}\}$ in the centre of the
$\boldsymbol {\varPhi }_P=\{\mathcal {A}_{ij}\mathcal {H}^P_{ji},-\mathcal {A}_{ij}\mathcal {A}_{jk}\mathcal {H}^P_{ki}\}$ in the centre of the ![]() $Q$–
$Q$–![]() $R$ plane, and in the Vieillefosse tail during the inverse and direct evolutions. See figure 10(b) for reference. In regions where gradients are not strong, the non-local component of the pressure Hessian appears decorrelated from the local dynamics, with a large scatter of the data with respect to the mean. In the Vieillefosse tail the non-local component of the pressure Hessian counteracts the RE dynamics and the action of the non-local component of the pressure Hessian over
$R$ plane, and in the Vieillefosse tail during the inverse and direct evolutions. See figure 10(b) for reference. In regions where gradients are not strong, the non-local component of the pressure Hessian appears decorrelated from the local dynamics, with a large scatter of the data with respect to the mean. In the Vieillefosse tail the non-local component of the pressure Hessian counteracts the RE dynamics and the action of the non-local component of the pressure Hessian over ![]() $Q$ and
$Q$ and ![]() $R$ appears more correlated. When time is reversed, these correlations are necessary to sustain the antitail. As shown in § 6.3, the contraction of the antitail is the first identifiable process in the transition from the inverse to the direct cascade, which indicates that these correlations are quickly destroyed under perturbations.
$R$ appears more correlated. When time is reversed, these correlations are necessary to sustain the antitail. As shown in § 6.3, the contraction of the antitail is the first identifiable process in the transition from the inverse to the direct cascade, which indicates that these correlations are quickly destroyed under perturbations.

Figure 10. (a) Joint probability density function of the components of the probability transport velocities due to the non-local part of the pressure Hessian, ![]() $\{\mathcal {A}_{ij}\mathcal {H}^P_{ji},-\mathcal {A}_{ij}\mathcal {A}_{jk}\mathcal {H}^P_{ki}\}$, conditioned to different areas in the
$\{\mathcal {A}_{ij}\mathcal {H}^P_{ji},-\mathcal {A}_{ij}\mathcal {A}_{jk}\mathcal {H}^P_{ki}\}$, conditioned to different areas in the ![]() $Q$–
$Q$–![]() $R$ plane:
$R$ plane: ![]() $-\cdot -$,
$-\cdot -$, ![]() $|Q|<1$ and
$|Q|<1$ and ![]() $|R|<1$, dashed region in (b); – – –, dashed blue line,
$|R|<1$, dashed region in (b); – – –, dashed blue line, ![]() $Q<-1$ in the direct evolution, shaded region in (b); ——, solid red line,
$Q<-1$ in the direct evolution, shaded region in (b); ——, solid red line, ![]() $Q<-1$ in the inverse evolution, shaded region in (b). Quantities normalised with
$Q<-1$ in the inverse evolution, shaded region in (b). Quantities normalised with ![]() $t_Q$.
$t_Q$.
While the generation of topologies in the Vieillefosse tail is a direct consequence of the local self-amplification of the rate-of-strain tensor, the generation of topologies in the antitail requires a global configuration of the complete flow field that counteracts this amplification through the non-local action of the pressure Hessian. This scenario appears intuitively unlikely, suggesting that only specially organised flows are able to produce such action (Popper Reference Popper1956). This is the case of the initial conditions used for the inverse evolutions, which conserve all the information of the direct cascade process. In particular, they retain the correlations between the rate-of-strain tensor and the non-local contribution of the pressure Hessian in the Vieillefosse tail, thus inhibiting the breakdown of the antitail in the inverse cascade.
7. Conclusions
We have studied a microscopically reversible turbulent system constructed using a reversible SGS model to explore the energy cascade as an entropy-driven process. In this system inverse and direct energy cascades over the full domain are possible, but only the latter are experimentally observed due to the statistical irreversibility of the dynamics in the inertial range. In this paper we explain the origin of this irreversibility by focusing on the dynamics of the energy cascade in physical space.
We show in § 4.3 that, in this reversible system, sustained inverse cascades are a consequence of inertial mechanisms, while the SGS model only acts as a source of energy. By reversing the energy cascade of a system with an irreversible SGS model, we present strong evidences that microscopic reversibility is a fundamental property of inertial dynamics, independent of the dissipation.
In § 5.1 we characterise the distribution of inverse trajectories in phase space. By perturbing inverse phase-space trajectories within the ‘antiattractor’, i.e the set of turbulent flows generated by evolving direct cascades backwards in time, we show that inverse evolutions exist in a wide region of phase space, separated from the direct evolutions. The perturbed inverse trajectories diverge from the original trajectories, and eventually evolve towards the turbulence ‘attractor’, which is composed almost exclusively by trajectories with a direct energy cascade. Inverse cascades are ‘unstable’. They can only be observed for a finite time, and it is extremely unlikely that they develop spontaneously.
In order to connect phase-space dynamics with the energy cascade, we have studied the spatial structure of the local energy fluxes in physical space using two common definitions of the fluxes, which are calculated at different scales by filtering the velocity field. The auto-correlation length of these fluxes is of the order of the filter width, and, when volume averaged for different sizes, their statistics are consistent with a space-local process. Although the two fluxes have similar mean, they are very different pointwise, particularly in the intensity and probability of backscatter. These differences disappear when the fluxes are averaged over volumes of the order of the filter width cubed. We conclude that the energy cascade is approximately local in physical space and robust to the definition of the energy fluxes on an average sense.
We have extended this analysis by studying the spatial correlation between local energy fluxes at different scales. The correlation between fluxes at scales separated by a factor of two is substantial, but significantly decreases when scales are separated by a factor of four, corroborating the reported scale locality of the cascade (Eyink Reference Eyink2005; Domaradzki, Teaca & Carati Reference Domaradzki, Teaca and Carati2009; Eyink & Aluie Reference Eyink and Aluie2009; Cardesa et al. Reference Cardesa, Vela-Martín and Jiménez2017). When conditioning these correlations to the sign of the fluxes, we find that they are strong for direct energy fluxes but weak for energy backscatter, revealing that, unlike direct energy transfer, backscatter is very shallow in scale space. Moreover, backscatter is very sensitive to the choice of the fluxes, and disappears when volume averaged over volumes of the order of the cubed filter width, suggesting that it represents spatial fluxes at the scale of the filter rather than an inverse energy cascade involving interactions at different scales.
Although the present work strongly emphasises the bidirectionality of the cascade, our results suggest that the dynamical significance of backscatter to the energy cascade is limited. Following the local fluctuation relations (Michel & Searles Reference Michel and Searles2013), we have attempted to estimate the probability of inverse energy cascades over the complete domain by quantifying the probability of volume-averaged inverse energy transfer events, but our results are not conclusive because these events disappear almost completely for small averaging volumes. Turbulence is sufficiently far from equilibrium as to preclude the observation of local inverse cascades, even in reduced regions of space. Although some representations of the energy fluxes can be negative locally, this does not seem to imply a local inverse energy cascade that develops against the tendency of the system towards equilibrium.
Finally, we have compared the structure of the direct and inverse cascades through the study of the invariants of the velocity gradient tensor, ![]() $Q$ and
$Q$ and ![]() $R$, and its CMTs. In the direct evolutions the joint probability density function of
$R$, and its CMTs. In the direct evolutions the joint probability density function of ![]() $Q$ and
$Q$ and ![]() $R$ forms the classical teardrop, with dominant vortex stretching in
$R$ forms the classical teardrop, with dominant vortex stretching in ![]() $Q>0$ and a Vieillefosse (Reference Vieillefosse1984) tail in
$Q>0$ and a Vieillefosse (Reference Vieillefosse1984) tail in ![]() $Q<0$, while in the inverse evolutions
$Q<0$, while in the inverse evolutions ![]() $Q$ and
$Q$ and ![]() $R$ form an inverse teardrop, with dominant vortex compression in
$R$ form an inverse teardrop, with dominant vortex compression in ![]() $Q>0$ and an antitail in
$Q>0$ and an antitail in ![]() $Q<0$. We have quantified these differences using an asymmetry function in the
$Q<0$. We have quantified these differences using an asymmetry function in the ![]() $Q$–
$Q$–![]() $R$ plane, which reveals that most of the temporal asymmetry is located in the
$R$ plane, which reveals that most of the temporal asymmetry is located in the ![]() $Q<0$ semiplane, suggesting a strong connection between the structure of the rate-of-strain tensor and the direction of the system in time. In the direct cascade the rate-of-strain tensor has predominantly one negative and two positive eigenvalues, while in the inverse cascade it has two negative eigenvalues and one positive eigenvalue. On the other hand, it is more challenging to distinguish the inverse from the direct cascade by only considering the dynamics of intense enstrophy regions: the stretching and compression of intense vorticity are present in both the direct and the inverse cascade.
$Q<0$ semiplane, suggesting a strong connection between the structure of the rate-of-strain tensor and the direction of the system in time. In the direct cascade the rate-of-strain tensor has predominantly one negative and two positive eigenvalues, while in the inverse cascade it has two negative eigenvalues and one positive eigenvalue. On the other hand, it is more challenging to distinguish the inverse from the direct cascade by only considering the dynamics of intense enstrophy regions: the stretching and compression of intense vorticity are present in both the direct and the inverse cascade.
The CMTs convey a similar picture. They display similar behaviour in ![]() $Q>0$ regardless of the direction of the cascade, but undergo fundamental changes in
$Q>0$ regardless of the direction of the cascade, but undergo fundamental changes in ![]() $Q<0$ when the system is reversed in time. In the direct evolution the non-local action of the pressure Hessian opposes the formation of intense gradients in the Vieillefosse tail, counteracting the RE dynamics, while in the inverse cascade it favours the formation of the antitail, also counteracting the RE dynamics.
$Q<0$ when the system is reversed in time. In the direct evolution the non-local action of the pressure Hessian opposes the formation of intense gradients in the Vieillefosse tail, counteracting the RE dynamics, while in the inverse cascade it favours the formation of the antitail, also counteracting the RE dynamics.
We have extended this analysis to inverse phase-space trajectories outside the antiattractor. The transition from an inverse to a direct cascade is marked by the disappearance of the antitail and the appearance of a regular Vieillefosse tail, but the statistics of enstrophy-dominated regions do not change substantially in this transition.
To further corroborate the strong connection between the Vieillefosse tail and the direction of the cascade, we have conditioned the statistics of local energy fluxes to the invariants of the filtered velocity gradient tensor at the same scale. In the direct evolutions the most intense energy transfer events are related to structures in the Vieillefosse tail, which contribute the most to the total energy fluxes. On the other hand, the antitail is responsible for most inverse energy transfer in the inverse evolutions.
In view of these results, we point to the negligible probability of topologies in the antitail as the cause of the low probability of inverse cascades, and propose an entropic argument to explain this fact. The generation of topologies along the Vieillefosse tail is encoded in the pointwise interaction of the velocity gradients, and is strictly local. Any possible organisation of the vorticity vector and the rate-of-strain tensor will generate topologies in the Vieillefosse tail under the action of RE dynamics. On the other hand, the formation and maintenance of the antitail requires the global action of the non-local component of the pressure Hessian, which involves a large number of degrees of freedom, to generate intense strain with a negative intermediate eigenvalue. While the dynamics of any flow field, even random ones, leads to the generation of a Vieillefosse tail due to RE dynamics, only very special flow fields are sufficiently organised so as to counteract the RE dynamics and form an antitail. Assuming that global fluctuation relations (Evans & Searles Reference Evans and Searles2002) apply to turbulent flows, the probability of observing such organised states is inversely proportional to the exponential of the number of degrees of freedom of the system, which explains why stochastic and deterministic reduced-order models of the cascade exhibit statistical irreversibility despite their reduced number of degrees of freedom (Biferale Reference Biferale2003; Meneveau Reference Meneveau2011).
Our results stress the importance of the rate-of-strain tensor on the dynamics of the energy cascade, and agree with other studies that suggest that the role of vorticity in turbulence dynamics is perhaps overemphasized (Tsinober Reference Tsinober1998; Carbone & Bragg Reference Carbone and Bragg2020; Johnson Reference Johnson2020). While a change in the sign of vorticity does not change the fundamental dynamics of vortices, for instance, in the Burgers (Reference Burgers1948) model, a change in the sign of the rate-of-strain tensor reverses the evolution of both the enstrophy and the strain in the inviscid case. This is evident in the evolution equations of the strain and the enstrophy, (6.3) and (6.4), which are odd in the rate-of-strain tensor and even in the vorticity vector. Although the rate-of-strain tensor and the vorticity vector are not independent, but tied by kinematic relations, and changing the sign of one changes the sign of the other, it is the rate-of-strain tensor that reflects most of the statistical irreversibility of turbulent flows. A local observer wishing to establish the direction of the cascade in the inertial scales of turbulence should focus on the dynamics of the rate-of-strain tensor, rather than on the dynamics of the vorticity vector.
Funding
This work was supported by the European Research Council COTURB project ERC-2014.AdG-669505.
Declaration of interests
The authors report no conflict of interest.