Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-12T02:39:23.361Z Has data issue: false hasContentIssue false
  • English
  • Français

Is the Taylor–Proudman theorem exact in unbounded domains? Case study of the three-dimensional stability of a vortex pair in a rapidly rotating fluid

Published online by Cambridge University Press:  08 June 2021

Paul Billant Open the ORCID record for Paul Billant [Opens in a new window]
Paul Billant*
Affiliation:
Laboratoire d'Hydrodynamique (LadHyX), CNRS, Ecole Polytechnique, Institut Polytechnique de Paris, 91120Palaiseau, France
*
†Email address for correspondence: billant@ladhyx.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Owing to the Taylor–Proudman theorem, it is generally believed that rotating flows should have two-dimensional dynamics for rapid background rotation. Yet, we show that two infinitely long counter-rotating vertical vortices always remain unstable to three-dimensional perturbations even for large rotation rate about the vertical axis. The dominant instability consists of quasi-antisymmetric displacements of the two vortices. Its growth rate is independent of the rotation rate when it is sufficiently large, while the most amplified vertical wavelength scales like the rotation rate. Direct numerical simulations show that the instability leads ultimately to a full three-dimensional breakdown of the vortex pair. In other words, a two-dimensional vortex pair will spontaneously develop three-dimensional variations even in the limit of infinite rotation rate but the wavelength will tend to infinity. This implies that the Taylor–Proudman theorem can be strictly valid only in vertically bounded flows. The scaling for the wavelength is next generalized by showing that the typical vertical scale in rapidly rotating unbounded flows is $L_v \sim L_h/Ro$, where $L_h$ is the horizontal scale and $Ro$ the Rossby number. This scaling law is shown to derive from a self-similarity of the Navier–Stokes equations for $Ro \ll 1$. The resulting reduced equations are identical to those obtained first by Julien et al. (Theor. Comput. Fluid Dyn., vol. 11, issue 3–4, 1998, pp. 251–261) and Nazarenko & Schekochihin (J. Fluid Mech., vol. 677, 2011, pp. 134–153) by means of multiscale analyses in the cases of rotating convection or turbulence. The self-similarity demonstrated herein suggests that these reduced equations are valid for any rapidly rotating unbounded flow.

JFM classification

Vortex Flows: Vortex instability Geophysical and Geological Flows: Rotating flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , R1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alexakis, A. & Biferale, L. 2018 Cascades and transitions in turbulent flows. Phys. Rep. 767, 1–101.CrossRefGoogle Scholar
Arobone, E. & Sarkar, S. 2012 Evolution of a stratified rotating shear layer with horizontal shear. Part I. Linear stability. J. Fluid Mech. 703, 29–48.10.1017/jfm.2012.183CrossRefGoogle Scholar
Billant, P., Brancher, P. & Chomaz, J.-M. 1999 Three-dimensional stability of a vortex pair. Phys. Fluids 11, 2069–2077.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2000 Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.CrossRefGoogle Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.10.1063/1.1369125CrossRefGoogle Scholar
Cambon, C., Rubinstein, R. & Godeferd, F.S. 2004 Advances in wave turbulence: rapidly rotating flows. New J. Phys. 6 (1), 73.CrossRefGoogle Scholar
Crow, S.C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8, 2172–2179.CrossRefGoogle Scholar
Davidson, P.A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.CrossRefGoogle Scholar
Deloncle, A., Billant, P. & Chomaz, J.-M. 2008 Nonlinear evolution of the zigzag instability in stratified fluids: a shortcut on the route to dissipation. J. Fluid Mech. 599, 229–239.10.1017/S0022112007000109CrossRefGoogle Scholar
Deusebio, E., Boffetta, G., Lindborg, E. & Musacchio, S. 2014 Dimensional transition in rotating turbulence. Phys. Rev. E 90 (2), 023005.CrossRefGoogle ScholarPubMed
Gallaire, F. & Rousset, F. 2006 Short-wave centrifugal instability in the vicinity of vanishing total vorticity streamlines. Phys. Fluids 18 (5), 058102.CrossRefGoogle Scholar
Gallet, B. 2015 Exact two-dimensionalization of rapidly rotating large-Reynolds-number flows. J. Fluid Mech. 783, 412–447.10.1017/jfm.2015.569CrossRefGoogle Scholar
Godeferd, F.S., Cambon, C. & Leblanc, S. 2001 Zonal approach to centrifugal, elliptic and hyperbolic instabilities in stuart vortices with external rotation. J. Fluid Mech. 449, 1–37.CrossRefGoogle Scholar
Godeferd, F.S. & Moisy, F. 2015 Structure and dynamics of rotating turbulence: a review of recent experimental and numerical results. Appl. Mech. Rev. 67 (3), 030802.CrossRefGoogle Scholar
Greenspan, H.P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Julien, K. & Knobloch, E. 2007 Reduced models for fluid flows with strong constraints. J. Math. Phys. 48 (6), 065405.CrossRefGoogle Scholar
Julien, K., Knobloch, E. & Werne, J. 1998 A new class of equations for rotationally constrained flows. Theor. Comput. Fluid Dyn. 11 (3–4), 251–261.10.1007/s001620050092CrossRefGoogle Scholar
van Kan, A. & Alexakis, A. 2020 Critical transition in fast-rotating turbulence within highly elongated domains. J. Fluid Mech. 899, A33.10.1017/jfm.2020.443CrossRefGoogle Scholar
Kerswell, R.R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34, 83–113.CrossRefGoogle Scholar
Kloosterziel, R.C. & van Heijst, G.J.F. 1991 An experimental study of unstable barotropic vortices in a rotating fluid. J. Fluid Mech. 223, 1–24.CrossRefGoogle Scholar
Le Dizes, S. 2000 Three-dimensional instability of a multipolar vortex in a rotating flow. Phys. Fluids 12 (11), 2762–2774.CrossRefGoogle Scholar
Leweke, T., Le Dizès, S. & Williamson, C.H.K. 2016 Dynamics and instabilities of vortex pairs. Annu. Rev. Fluid Mech. 48, 507–541.CrossRefGoogle Scholar
Moisy, F., Morize, C., Rabaud, M. & Sommeria, J. 2011 Decay laws, anisotropy and cyclone-anticyclone asymmetry in decaying rotating turbulence. J. Fluid Mech. 666, 5–35.10.1017/S0022112010003733CrossRefGoogle Scholar
Nazarenko, S.V. & Schekochihin, A.A. 2011 Critical balance in magnetohydrodynamic, rotating and stratified turbulence: towards a universal scaling conjecture. J. Fluid Mech. 677, 134–153.CrossRefGoogle Scholar
Potylitsin, P.G. & Peltier, W.R. 1999 Three-dimensional destabilization of Stuart vortices: the influence of rotation and ellipticity. J. Fluid Mech. 387, 205–226.CrossRefGoogle Scholar
Seshasayanan, K. & Gallet, B. 2020 Onset of three-dimensionality in rapidly rotating turbulent flows. J. Fluid Mech. 901, R5.CrossRefGoogle Scholar
Sipp, D. & Jacquin, L. 2000 Three-dimensional centrifugal-type instabilities of two-dimensional flows in rotating systems. Phys. Fluids 12 (7), 1740–1748.CrossRefGoogle Scholar
Sipp, D. & Jacquin, L. 2003 Widnall instabilities in vortex pairs. Phys. Fluids 15, 1861–1874.CrossRefGoogle Scholar
Sipp, D., Jacquin, L. & Cossu, C. 2000 Self-adaptation and viscous selection in concentrated two-dimensional dipoles. Phys. Fluids 12 (2), 245–248.CrossRefGoogle Scholar
Sipp, D., Lauga, E. & Jacquin, L. 1999 Vortices in rotating systems: centrifugal, elliptic and hyperbolic type instabilities. Phys. Fluids 11 (12), 3716–3728.CrossRefGoogle Scholar
Sprague, M., Julien, K., Knobloch, E. & Werne, J. 2006 Numerical simulation of an asymptotically reduced system for rotationally constrained convection. J. Fluid Mech. 551, 141–174.10.1017/S0022112005008499CrossRefGoogle Scholar

Billant supplementary movie 1

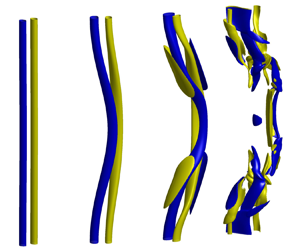
Movie 1 (a) Three-dimensional contours of the vertical vorticity in a Direct Numerical Simulation for Ro=0.76, b=3 and Re=500. Yellow and blue contours represent respectively plus and minus 50% of the vertical average of the maximum vertical vorticity in each horizontal plane. Three horizontal cross-sections of the vertical vorticity in the planes z=L_z/2 (b), z=3L_z/4 (c) and z=L_z (d) are also displayed. The location of these cross-sections are indicated by dashed lines with different color in (a). Note that only a portion of the computational domain is shown.

Download Billant supplementary movie 1(Video)
Video 8.3 MB

Billant supplementary movie 2

Movie 2 (a) Three-dimensional contours of the vertical vorticity in a Direct Numerical Simulation for Ro=1.53, b=3 and Re=500. Yellow and blue contours represent respectively plus and minus 50% of the vertical average of the maximum vertical vorticity in each horizontal plane. Three horizontal cross-sections of the vertical vorticity in the planes z=L_z/2 (b), z=3L_z/4 (c) and z=L_z (d) are also displayed. The location of these cross-sections are indicated by dashed lines with different color in (a). Note that only a portion of the computational domain is shown.

Download Billant supplementary movie 2(Video)
Video 7.7 MB