Hostname: page-component-848d4c4894-pftt2 Total loading time: 0 Render date: 2024-06-07T22:01:33.725Z Has data issue: false hasContentIssue false
  • English
  • Français

A macrotransport equation for the Hele-Shaw flow of a concentrated suspension

Published online by Cambridge University Press:  09 August 2021

Sourojeet Chakraborty Open the ORCID record for Sourojeet Chakraborty [Opens in a new window]  and
Arun Ramachandran Open the ORCID record for Arun Ramachandran [Opens in a new window]
Sourojeet Chakraborty
Affiliation:
Chemical Engineering and Applied Chemistry, University of Toronto, Toronto, ONM5S 3E5, Canada
Arun Ramachandran*
Affiliation:
Chemical Engineering and Applied Chemistry, University of Toronto, Toronto, ONM5S 3E5, Canada
*
†Email address for correspondence: engrarun@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

A depth-averaged, convection-dispersion equation is derived for the particle volume fraction distribution in the pressure-driven flow of a concentrated suspension of neutrally buoyant, non-colloidal particles between two parallel plates, by implementing a two-time-scale perturbation expansion of the suspension balance model (Nott & Brady, J. Fluid Mech., vol. 275, 1994, pp. 157–199) coupled with the constitutive equations of Zarraga et al. (J. Rheol., vol. 52, issue 2, 2000, pp. 185–220). 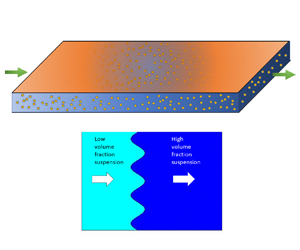The Taylor-dispersion coefficient in the macrotransport equation scales as $U_c^{\prime}B^{\prime 3}/a^{\prime 2}$, where $U_c^{\prime}$ is the characteristic depth-averaged velocity, $B^{\prime}$ is the half-depth of the channel and $a^{\prime}$ is the particle radius. Taylor dispersion relaxes gradients in the depth-averaged volume fraction along the local velocity vector. Perpendicular to the flow, however, only shear-induced migration can cause particle redistribution, leading to fluxes down gradients in volume fraction, shear rate and streamline curvature that scale as $U_c^{\prime}a^{\prime 2}/B^{\prime}$. To determine the velocity and particle distributions in Hele-Shaw suspension flows, one only needs to solve two coupled partial differential equations in the pressure and the depth-averaged volume fraction, achievable on commercially available solvers. Analogous to the macrotransport equation for suspension flow through a circular tube (Ramachandran, J. Fluid Mech., vol. 734, 2013, pp. 219–252), the evolution of the particle volume fraction distribution is dependent only on the total strain experienced by the suspension, and is independent of the suspension velocity scale. However, unlike the tube problem, a positive concentration gradient along the flow direction is susceptible to viscous miscible fingering. A linear stability analysis performed for a step increase in the volume fraction in the direction of flow with a velocity $U^{\prime}$ reveals that the growth rate and wavenumber corresponding to fastest growing mode scale as $U^{\prime}a^{\prime 2}/B^{\prime 3}$ and $a^{\prime 2/3}/B^{\prime 5/3}$, respectively.

JFM classification

Complex Fluids: Suspensions Low-Reynolds-number flows: Hele-Shaw flows Instability: Instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 924 , 10 October 2021 , A1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Batchelor, G.K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.CrossRefGoogle Scholar
Ben, Y., Demekhin, E.A. & Chang, H.-C. 2002 A spectral theory for small amplitude miscible fingering. Phys. Fluids 14 (3), 999–1010.CrossRefGoogle Scholar
Bischofberger, I., Ramachandran, R. & Nagel, S.R. 2014 Fingering versus stability in the limit of zero interfacial tension. Nat. Commun. 5, 5265.CrossRefGoogle ScholarPubMed
Boyer, F., Guazzelli, E. & Pouliquen, O. 2011 a Unifying suspension and granular rheology. Phys. Rev. Lett. 107 (18), 188301.CrossRefGoogle ScholarPubMed
Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 b Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.CrossRefGoogle Scholar
Brady, J.F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.CrossRefGoogle Scholar
Brenner, H. & Edwards, D.A. 1993 Macrotransport Processes. Butterworth-Heinemann.Google Scholar
Chapman, B.K. 1990 Shear-induced migration phenomena in concentrated suspensions. PhD thesis, University of Notre Dame.Google Scholar
Christov, I.C. & Stone, H.A. 2014 Shear dispersion in dense granular flows. Granul. Matt. 16, 509–515.CrossRefGoogle Scholar
Dontsov, E.V., Boronin, S.A., Osiptsov, A.A. & Derbyshev, D.Y. 2019 Lubrication model of suspension flow in ahydraulic fracture with frictional rheology for shear-induced migration and jamming. Proc. R. Soc. A 475, 1–24.CrossRefGoogle ScholarPubMed
Dontsov, E.V. & Peirce, A.P. 2014 Slurry flow, gravitational settling and a proppant transport model for hydraulic fractures. J. Fluid Mech. 760, 567–590.CrossRefGoogle Scholar
Drew, D.A. & Lahey, R.T. 1993 Analytical modeling of multiphase flow. In Particulate Two-Phase Flow (ed. M. Roco), p. 509. Butterworth.Google Scholar
Einstein, A. 1906 Eine neue Bestimmung der Molekiidimensionen. Ann. Physik 19, 289–306.CrossRefGoogle Scholar
Fang, Z., Mammoli, A.A., Brady, J.F., Ingber, M.S., Mondy, L.A. & Graham, A.L. 2002 Flow-aligned tensor models for suspension flows. Intl J. Multiphase Flow 28 (1), 137–166.CrossRefGoogle Scholar
Fiore, A. & Swan, J.W. 2019 Fast Stokesian dynamics. J. Fluid Mech. 878, 544–597.CrossRefGoogle Scholar
Gao, C. & Gilchrist, J.F. 2008 Shear-induced particle migration in one-, two-, and three-dimensional flows. Phys. Rev. E 77 (2), 025301.CrossRefGoogle ScholarPubMed
Griffiths, I.M. & Stone, H.A. 2012 Axial dispersion via shear-enhanced diffusion in colloidal suspensions. Europhys. Lett. 97, 58005.CrossRefGoogle Scholar
Guazzelli, E. & Morris, J.F. 2011 A Physical Introduction to Suspension Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Hampton, R.E., Mammoli, A.A., Graham, A.L. & Tetlow, N. 1997 Migration of particles undergoing pressure-driven flow in a circular conduit. J. Rheol. 41 (3), 621–640.CrossRefGoogle Scholar
Hill, S. 1952 Channelling in packed columns. Chem. Engng Sci. 1 (6), 247–253.CrossRefGoogle Scholar
Hinch, E.J. 1991 Perturbation Methods. Cambridge University Press.CrossRefGoogle Scholar
Homsy, G.M. 1987 Viscous fingering in porous media. Annu. Rev. Fluid Mech. 19, 271–311.CrossRefGoogle Scholar
Hormozi, S. & Frigaard, I.A. 2017 Dispersion of solids in fracturing flows of yield stress fluids. J. Fluid Mech. 830, 93–137.CrossRefGoogle Scholar
Ingber, M.S., Feng, S., Graham, A.L. & Brenner, H. 2008 The analysis of self-diffusion and migration of rough spheres in nonlinear shear flow using a traction-corrected boundary element method. J. Fluid Mech. 598, 267–292.CrossRefGoogle Scholar
Jackson, R. 1997 Locally averaged equations of motion for a mixture of identical spherical particles and a Newtonian fluid. Chem. Engng Sci. 52 (15), 2457–2469.CrossRefGoogle Scholar
Jana, S.C., Kapoor, B. & Acrivos, A. 1995 Apparent wall slip velocity coefficients in concentrated suspensions of noncolloidal particles. J. Rheol. 39 (6), 1123–1132.CrossRefGoogle Scholar
Jenkins, J.T. & McTigue, D.F. 1990 Two Phase Flows and Waves, pp. 70–79. Springer.CrossRefGoogle Scholar
Karnis, A. & Mason, S.G. 1967 The flow of suspensions through tubes. VI. Meniscus effects. J. Colloid Interface Sci. 23, 120–133.CrossRefGoogle Scholar
Kim, S. & Karrila, S.J. 2005 Microhydrodynamics: Principles and Selected Applications. Dover.Google Scholar
Koh, C.J., Hookham, P. & Leal, L.G. 1994 An experimental investigation of concentrated suspension flows in a rectangular channel. J. Fluid Mech. 266, 1–32.CrossRefGoogle Scholar
Lajeunesse, E., Martin, J., Rakotomalala, N., Salin, D. & Yortsos, Y.C. 1999 Miscible displacement in a Hele-Shaw cell at high rates. J. Fluid Mech. 398, 299–319.CrossRefGoogle Scholar
Lam, Y.C., Chen, X., Tam, K.C. & Yu, S.C.M. 2003 Simulation of particle migration of powder-resin system in injection molding. Trans ASME: J. Manuf. Sci. E 125 (3), 538–547.Google Scholar
Leal, L.G. 2007 Advanced Transport Phenomena. Cambridge University Press.CrossRefGoogle Scholar
Lecampion, B. & Garagash, D.I. 2014 Confined flow of suspensions modelled by a frictional rheology. J. Fluid Mech. 759, 197–235.CrossRefGoogle Scholar
Leighton, D. & Acrivos, A. 1987 The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.CrossRefGoogle Scholar
Luo, R., Chen, Y. & Lee, S. 2018 Particle-induced viscous fingering: review and outlook. Phys. Rev. Fluids 3 (11), 110502.CrossRefGoogle Scholar
Luo, R., Chen, Y. & Lee, S. 2020 Particle-induced viscous fingering: continuum limit. Phys. Rev. Fluids 5 (9), 094301.CrossRefGoogle Scholar
Lyon, M.K. & Leal, L.G. 1998 An experimental study of the motion of concentrated suspensions in two-dimensional channel flow. Part 1. Monodisperse systems. J. Fluid Mech. 363, 25–56.CrossRefGoogle Scholar
Miller, R.M. & Morris, J.F. 2006 Normal stress-driven migration and axial development in pressure-driven flow of concentrated suspensions. J. Non-Newtonian Fluid Mech. 135 (2–3), 149–165.CrossRefGoogle Scholar
Mills, P. & Snabre, P. 1995 Rheology and structure of concentrated suspension of hard spheres: shear-induced particle migration. J. Phys. II 5, 1597–1608.Google Scholar
Morris, J.F. & Boulay, F. 1999 Curvilinear flows of non-colloidal suspensions: the role of normal stresses. J. Rheol. 43 (5), 1213–1237.CrossRefGoogle Scholar
Municchi, F., Nagrani, P.P. & Christov, I.C. 2019 A two-fluid model for numerical simulation of shear-dominated suspension flows. Intl J. Multiphase Flow 120, 103079.CrossRefGoogle Scholar
Nott, P.R. & Brady, J.F. 1994 Pressure-driven flow of suspensions: simulations and theory. J. Fluid Mech. 275, 157–199.CrossRefGoogle Scholar
Pagitsas, M., Nadim, A. & Brenner, H. 1986 Multiple time scale analysis of macrotransport processes. Physica A 135, 533–550.CrossRefGoogle Scholar
Phillips, R.J., Armstrong, R.C., Brown, R.A., Graham, A.L. & Abbott, J.R. 1992 A constitutive model for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A 4, 30–40.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.CrossRefGoogle Scholar
Probstein, R.F. 1994 Physicochemical Hydrodynamics. John Wiley and Sons.CrossRefGoogle Scholar
Ramachandran, A. 2013 A macrotransport equation for the particle distribution in the flow of a concentrated, non-colloidal suspension through a circular tube. J. Fluid Mech. 734, 219–252.CrossRefGoogle Scholar
Ramachandran, A. & Leighton, D.T. 2007 a The effect of gravity on the meniscus accumulation phenomenon in a tube. J. Rheol. 51 (5), 1073–1098.CrossRefGoogle Scholar
Ramachandran, A. & Leighton, D.T. 2007 b Viscous resuspension in a tube: the impact of secondary flows resulting from second normal stress differences. Phys. Fluids 19 (5), 055301.CrossRefGoogle Scholar
Ramachandran, A. & Leighton, D.T. 2008 The influence of secondary flows induced by normal stress differences on the shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 603, 207–243.CrossRefGoogle Scholar
Shamu, T.J., Zou, L., Kotzé, R., Wiklund, J. & Håkansson, U. 2020 Radial flow velocity profiles of a yield stress fluid between smooth parallel disks. Rheol. Acta 59, 239–254.CrossRefGoogle Scholar
Sierou, A. & Brady, J.F. 2001 Accelerated Stokesian dynamics simulations. J. Fluid Mech. 448, 115–146.CrossRefGoogle Scholar
Sune, L. & Maxey, M.R. 2003 Force-coupling method for particulate two-phase flow: Stokes flow. J. Comput. Phys. 184 (2), 381–405.Google Scholar
Tan, C.T. & Homsy, G.M. 1986 Stability of miscible displacements in porous media: rectilinear flow. Phys. Fluids 29 (11), 3549–3556.CrossRefGoogle Scholar
Tang, H., Grivas, W., Homentcovschi, D., Geer, J. & Singler, T. 2000 Stability considerations associated with the meniscoid particle band at advancing interfaces in Hele-Shaw suspension flows. Phys. Rev. Lett. 85 (10), 2112–2115.CrossRefGoogle ScholarPubMed
Taylor, G. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond.A 219 (1137), 186–203.Google Scholar
Videbaek, T.E. & Nagel, S.R. 2019 Diffusion-driven transition between two regimes of viscous fingering. Phys. Rev. Fluids 4 (3), 033902.CrossRefGoogle Scholar
Wong, J., Lindstrom, M. & Bertozzi, A.L. 2019 Fast equilibration dynamics of viscous particle-laden flow in an inclined channel. J. Fluid Mech. 879, 28–53.CrossRefGoogle Scholar
Wooding, R.A. 1962 The stability of an interface between miscible fluids in a porous medium. Z. Angew. Math. Phys. 13, 255–265.CrossRefGoogle Scholar
Yadav, S., Reddy, M.M. & Singh, A. 2016 Shear-induced migration of concentrated suspension through Y-shaped bifurcation channels. Particul. Sci. Technol. 34 (1), 83–95.CrossRefGoogle Scholar
Yeo, K. & Maxey, M.R. 2011 Numerical simulations of concentrated suspensions of monodisperse particles in a Poiseuille flow. J. Fluid Mech. 682, 491–518.CrossRefGoogle Scholar
Zarraga, I.E., Hill, D.A. & Leighton, D.T. 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 52 (2), 185–220.CrossRefGoogle Scholar