Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-09T00:05:19.690Z Has data issue: false hasContentIssue false
  • English
  • Français

A new multi-layer irrotational Boussinesq-type model for highly nonlinear and dispersive surface waves over a mildly sloping seabed

Published online by Cambridge University Press:  09 March 2018

Z. B. Liu ,
K. Z. Fang Open the ORCID record for K. Z. Fang [Opens in a new window]  and
Y. Z. Cheng
Z. B. Liu*
Affiliation:
Transportation Engineering College, Dalian Maritime University, Dalian, 116026, PR China State Key Laboratory of Coastal and Offshore Engineering, Ocean Engineering Joint Research Center of DUT-UWA, Dalian University of Technology, Dalian, 116024, PR China Key Laboratory of Water Sediment Science and Water Hazard Prevention of Hunan Province, Changsha University of Technology, Changsha, 410114, PR China
K. Z. Fang*
Affiliation:
State Key Laboratory of Coastal and Offshore Engineering, Ocean Engineering Joint Research Center of DUT-UWA, Dalian University of Technology, Dalian, 116024, PR China Key Laboratory of Water Sediment Science and Water Hazard Prevention of Hunan Province, Changsha University of Technology, Changsha, 410114, PR China
Y. Z. Cheng
Affiliation:
Key Laboratory of Water Sediment Science and Water Hazard Prevention of Hunan Province, Changsha University of Technology, Changsha, 410114, PR China
*
†Email addresses for correspondence: zhongbo_liu1976@163.com, kfang@dlut.edu.cn
†Email addresses for correspondence: zhongbo_liu1976@163.com, kfang@dlut.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A new multi-layer irrotational Boussinesq-type model is proposed for both linear and nonlinear surface water waves over mildly sloping seabeds. The model is formulated in terms of computational horizontal and vertical velocity components within each layer and satisfies exact kinematic and dynamic free-surface conditions as well as kinematic seabed conditions. Using a Stokes-type expansion, a theoretical analysis of the new multi-layer model is carried out to examine both linear and nonlinear properties, including wave celerity, velocity profiles, shoaling amplitude, second- and third-order transfer functions and amplitude dispersion. The dispersive coefficients in the governing equations are determined by optimizing the linear celerity or linear velocity profiles. For example, the four-layer model shows extremely high accuracy and is applicable up to 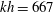$kh=667$–800 (where 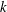$k$ is the wavenumber and 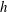$h$ is a typical water depth) with a 1 % error in wave phase celerity, and up to 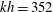$kh=352$–423 with a 1 % error in the linear velocity components. The super- and subharmonic transfer functions are extremely accurate up to 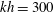$kh=300$ (1 % error), the third-order harmonics and amplitude dispersion are accurate up to 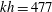$kh=477$ (1 % error), and the shoaling property is optimized to cover the range of 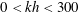$0<kh<300$, which presents a 0.06 % tolerance error in shoaling amplitude. The high-accuracy nature of the model increases its suitability for simulating random wave propagation from extremely deep to shallow waters over mildly sloping topographies. The model is implemented numerically on a non-staggered grid via a composite fourth-order Adams–Bashforth–Moulton time integration. The numerical results show good agreement with both the analytical solutions and experimental data.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 323 - 353
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agnon, Y., Madsen, P. A. & Schäffer, H. A. 1999 A new approach to higher order Boussinesq model. J. Fluid Mech. 399, 319–333.CrossRefGoogle Scholar
Antuono, M. & Brocchini, M. 2013 Beyond Boussinesq-type equations: semi-integrated models for coastal dynamics. Phys. Fluid 25, 016603.Google Scholar
Antuono, M., Liapidevskii, V. & Brocchini, M. 2009 Dispersive nonlinear shallow water equations. Stud. Appl. Maths 122 (1), 1–28.Google Scholar
Brocchini, M. 2013 A reasoned overview on Boussinesq-type models: the interplay between physics, mathematics and numerics. Proc. R. Soc. Lond. A 469, 20130496.Google Scholar
Chazel, F., Benoit, M., Ern, A. & Piperno, S. 2009 A double-layer Boussinesq-type model for highly nonlinear and dispersive waves. Proc. R. Soc. Lond. A 465, 2319–2346.Google Scholar
Chen, Y. & Liu, P. L.-F. 1995 Modified Boussinesq equations and associated parabolic models for water wave propagation. J. Fluid Mech. 288, 351–381.CrossRefGoogle Scholar
Fuhrman, D. R. 2004 Numerical Solutions of Boussinesq Equations for Fully Nonlinear and Extremely Dispersive Water Waves, pp. 20–21. Technical University of Denmark.Google Scholar
Galan, A., Simarro, G., Orfila, A., Simarro, J. & Liu, P. L.-F. 2012 Fully nonlinear model for water wave propagation from deep to shallow water. J. Waterways Port Coast. Ocean Engng 138, 362–371.Google Scholar
Gobbi, M. F. & Kirby, J. T. 2000 A fully nonlinear Boussinesq model for surface waves. Part 2: extension to O (kh)4 . J. Fluid Mech. 405, 181–210.Google Scholar
Hsiao, S. C., Lynett, P., Hwung, H. H. & Liu, P. L.-F. 2005 Numerical simulations of nonlinear short waves using a multilayer model. J. Engng Mech. 131, 231–243.Google Scholar
Kirby, J. T. 2016 Boussinesq models and their application to coastal processes across a wide range of scales. J. Waterway Port Coastal Ocean Engng 142 (6), 03116005.Google Scholar
Kirby, J. T., Wei, G., Chen, Q., Kennedy, A. B. & Dalrymple, R. A.1998 FUNWAVE 1.0, fully nonlinear Boussinesq wave model documentation and user’s manual. Res. Rep. no. CACR-98-06 University of Delaware, Newark, DE.Google Scholar
Liu, Z. B. & Fang, K. Z. 2015 Two-layer Boussinesq models for coastal water waves. Wave Motion 57, 88–111.Google Scholar
Liu, Z. B. & Fang, K. Z. 2016 A new two-layer Boussinesq model for coastal waves from deep to shallow water: derivation and analysis. Wave Motion 67, 1–14.Google Scholar
Liu, Z. B. & Sun, Z. C. 2005 Two sets of higher-order Boussinesq type equations for water waves. Ocean Engng 32, 1296–1310.Google Scholar
Lynett, P. & Liu, P. L.-F. 2004a A two-layer approach to wave modelling. Proc. R. Soc. Lond. A 460, 2637–2669.Google Scholar
Lynett, P. & Liu, P. L.-F. 2004b Linear analysis of the multi-layer model. Coast. Engng 51, 439–454.Google Scholar
Luth, H. R., Kloman, G. & Kitou, N.1994 Kinematics of waves breaking partially on an offshore bar LDV measurements of waves with and without a net onshore current. Rep. H-1573. Delft Hydraulics.Google Scholar
Madsen, P. A., Bingham, H. B. & Liu, H. 2002 A new Boussinesq method for fully nonlinear waves from shallow to deep water. J. Fluid Mech. 462, 1–30.Google Scholar
Madsen, P. A., Bingham, H. B. & Schäffer, H. A. 2003 Boussinesq-type formulations for fully nonlinear and extremely dispersive water waves: derivation and analysis. Proc. R. Soc. Lond. A 459, 1075–1104.Google Scholar
Madsen, P. A. & Fuhrman, D. R. 2010 High-order Boussinesq-type modeling of nonlinear wave phenomena in deep and shallow water. In Advances in Numerical Simulation of Nonlinear Water Waves (ed. Ma, Q. W.). World Scientific Publishing.Google Scholar
Madsen, P. A., Fuhrman, D. R. & Wang, B. 2006 A Boussinesq-type method for fully nonlinear waves interacting with a rapidly varying bathymetry. Coast. Engng 53, 487–504.Google Scholar
Madsen, P. A., Murray, R. & Sörensen, O. R. 1991 A new form of the Boussinesq equations with improved linear dispersion characteristics. Coast. Engng 15, 371–388.CrossRefGoogle Scholar
Madsen, P. A. & Schäffer, H. A. 1998 Higher-order Boussinesq-type equations for surface gravity waves: derivation and analysis. Phil. Trans. R. Soc. Lond. A 356, 3123–3184.CrossRefGoogle Scholar
Nwogu, O. 1993 Alternative from of Boussinesq equations for nearshore wave propagation. J. Waterways Port Coast. Ocean Engng 19, 618–638.CrossRefGoogle Scholar
Ohyama, T., Kiota, W. & Tada, A. 1995 Applicability of numerical models of nonlinear dispersive waves. Coast. Engng 24, 297–313.Google Scholar
Peregrine, D. H. 1967 Long waves on a beach. J. Fluid Mech. 27, 815–827.CrossRefGoogle Scholar
Simarro, G., Orfila, A. & Galan, A. 2013 Linear shoaling in Boussinesq-type wave propagation models. Coast. Engng 80, 100–106.Google Scholar
Skjelbreia, L. & Hendrickson, J. 1961 Fifth order gravity wave thoery. In Proc. 7th Int. Conf. on Coastal Engineering, pp. 184–196. ASCE.Google Scholar
Wei, G., Kirby, J. T., Grilli, S. T. & Subramanya, R. 1995 A fully nonlinear Boussinesq model for surface waves. Part 1. Highly nonlinear unsteady waves. J. Fluid Mech. 294, 71–92.Google Scholar
Williams, J. M. 1985 Tables of Progressive Gravity Waves. Pitman.Google Scholar
Zou, Z. L. 1999 Higher order Boussinesq equations. Ocean Engng 26, 767–792.Google Scholar
Zou, Z. L. 2000 A new form of high-order Boussinesq equations. Ocean Engng 27, 557–575.CrossRefGoogle Scholar
Zou, Z. L. & Fang, K. Z. 2008 Alternative forms of the higher-order Boussinesq equations: derivations and validations. Coast. Engng 55, 506–521.CrossRefGoogle Scholar