Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-03T16:14:06.964Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear travelling periodic waves for the Euler equations in three-layer flows

Published online by Cambridge University Press:  19 February 2024

Xin Guan Open the ORCID record for Xin Guan [Opens in a new window] ,
Alex Doak Open the ORCID record for Alex Doak [Opens in a new window] ,
Paul Milewski Open the ORCID record for Paul Milewski [Opens in a new window]  and
Jean-Marc Vanden-Broeck
Xin Guan*
Affiliation:
Department of Mathematics, University College London, London WC1E 6BT, UK
Alex Doak
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK
Paul Milewski
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, UK Department of Mathematics, Penn State University, Pennsylvania 16802, USA
Jean-Marc Vanden-Broeck
Affiliation:
Department of Mathematics, University College London, London WC1E 6BT, UK
*
†Email address for correspondence: xin.guan.20@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

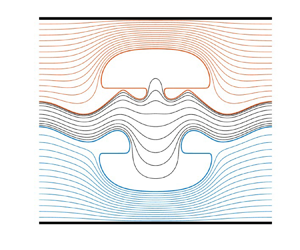
In this paper, we investigate periodic travelling waves in a three-layer system with the rigid-lid assumption. Solutions are recovered numerically using a boundary integral method. We consider the case where the density difference between the layers is small (i.e. a weakly stratified fluid). We consider the system both with and without the Boussinesq assumption to explore the effect the assumption has on the solution space. Periodic solutions of both mode-1 and mode-2 are found, and their bifurcation structure and limiting configurations are described in detail. Similarities are found with the two-layer case, where large-amplitude solutions are found to overhang with an internal angle of $120^{\circ }$. However, the addition of a second interface results in a richer bifurcation space, in part due to the existence of mode-2 waves and their resonance with mode-1 waves. New limiting profiles are found.

JFM classification

Waves/Free-surface Flows: Waves/Free-surface Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 981 , 25 February 2024 , A12
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akylas, T.R. & Grimshaw, R. 1992 Solitary internal waves with oscillatory tails. J. Fluid Mech. 242, 279–298.CrossRefGoogle Scholar
Barros, R. & Choi, W. 2011 Holmboe instability in non-Boussinesq fluids. Phys. Fluids 23 (12), 124103.CrossRefGoogle Scholar
Barros, R., Choi, W. & Milewski, P.A. 2020 Strongly nonlinear effects on internal solitary waves in three-layer flows. J. Fluid Mech. 883, A16.CrossRefGoogle Scholar
Boonkasame, A. & Milewski, P. 2012 The stability of large-amplitude shallow interfacial non-Boussinesq flows. Stud. Appl. Maths 128 (1), 40–58.CrossRefGoogle Scholar
Camassa, R., Chen, S., Falqui, G., Ortenzi, G. & Pedroni, M. 2012 An inertia ‘paradox’ for incompressible stratified Euler fluids. J. Fluid Mech. 695, 330–340.CrossRefGoogle Scholar
Carr, M., Davies, P.A. & Hoebers, R.P. 2015 Experiments on the structure and stability of mode-2 internal solitary-like waves propagating on an offset pycnocline. Phys. Fluids 27 (4), 046602.CrossRefGoogle Scholar
Chen, M.J. & Forbes, L.K. 2008 Steady periodic waves in a three-layer fluid with shear in the middle layer. J. Fluid Mech. 594, 157–181.CrossRefGoogle Scholar
Choi, W. & Camassa, R. 1999 Fully nonlinear internal waves in a two-fluid system. J. Fluid Mech. 396, 1–36.CrossRefGoogle Scholar
Chumakova, L., Menzaque, F.E., Milewski, P.A., Rosales, R.R., Tabak, E.G. & Turner, C.V. 2009 a Shear instability for stratified hydrostatic flows. Commun. Pure Appl. Maths 62 (2), 183–197.CrossRefGoogle Scholar
Chumakova, L., Menzaque, F.E., Milewski, P.A., Rosales, R.R., Tabak, E.G. & Turner, C.V. 2009 b Stability properties and nonlinear mappings of two and three–layer stratified flows. Stud. Appl. Maths 122 (2), 123–137.CrossRefGoogle Scholar
Doak, A., Barros, R. & Milewski, P.A. 2022 Large mode-2 internal solitary waves in three-layer flows. J. Fluid Mech. 953, A42.CrossRefGoogle Scholar
Evans, W.A.B. & Ford, M.J. 1996 An integral equation approach to internal (2-layer) solitary waves. Phys. Fluids 8 (8), 2032–2047.CrossRefGoogle Scholar
Grimshaw, R.H.J., Pelinovsky, E. & Talipova, T. 1997 The modified korteweg - de Vries equation in the theory of large-amplitude internal waves. Nonlinear Process. Geophys. 4 (4), 237–250.CrossRefGoogle Scholar
Grimshaw, R.H.J. & Pullin, D.I. 1986 Extreme interfacial waves. Phys. Fluids 29 (9), 2802–2807.CrossRefGoogle Scholar
Guan, X., Vanden-Broeck, J.-M. & Wang, Z. 2021 a New solutions for periodic interfacial gravity waves. J. Fluid Mech. 928, R5.CrossRefGoogle Scholar
Guan, X., Vanden-Broeck, J.-M., Wang, Z. & Dias, F. 2021 b A local model for the limiting configuration of interfacial solitary waves. J. Fluid Mech. 921, A9.CrossRefGoogle Scholar
Guha, A. & Raj, R. 2018 On the inertial effects of density variation in stratified shear flows. Phys. Fluids 30 (12), 126603.CrossRefGoogle Scholar
Heifetz, E. & Mak, J. 2015 Stratified shear flow instabilities in the non-Boussinesq regime. Phys. Fluids 27 (8), 086601.CrossRefGoogle Scholar
Jo, T.-C. & Choi, Y.-K. 2014 Dynamics of strongly nonlinear internal long waves in a three-layer fluid system. Ocean Sci. J. 49 (4), 357–366.CrossRefGoogle Scholar
Kurkina, O.E., Kurkin, A.A., Rouvinskaya, E.A. & Soomere, T. 2015 Propagation regimes of interfacial solitary waves in a three-layer fluid. Nonlinear Process. Geophys. 22 (2), 117–132.CrossRefGoogle Scholar
Lamb, K.G. 2000 Conjugate flows for a three-layer fluid. Phys. Fluids 12 (9), 2169–2185.CrossRefGoogle Scholar
Lewis, J.E., Lake, B.M. & Ko, D.R.S. 1974 On the interaction of internal waves and surface gravity waves. J. Fluid Mech. 63 (4), 773–800.CrossRefGoogle Scholar
Liapidevskii, V.Y. & Gavrilov, N.V. 2018 Large internal solitary waves in shallow waters. In The Ocean in Motion, pp. 87–108. Springer.CrossRefGoogle Scholar
Maklakov, D.V. & Sharipov, R.R. 2018 Almost limiting configurations of steady interfacial overhanging gravity waves. J. Fluid Mech. 856, 673–708.CrossRefGoogle Scholar
Miyata, M. 1988 Long Internal Waves of Large Amplitude, pp. 399–406. Springer.CrossRefGoogle Scholar
Ostrovsky, L.A. & Stepanyants, Y.A. 2005 Internal solitons in laboratory experiments: comparison with theoretical models. Chaos 15 (3), 037111.CrossRefGoogle ScholarPubMed
Rusås, P.-O. 2000 On nonlinear internal waves in two- and three-layer fluids. PhD thesis, University of Oslo.Google Scholar
Rusås, P.-O. & Grue, J. 2002 Solitary waves and conjugate flows in a three-layer fluid. Eur. J. Mech. (B/Fluids) 21 (2), 185–206.CrossRefGoogle Scholar
Saffman, P.G. & Yuen, H.C. 1982 Finite-amplitude interfacial waves in the presence of a current. J. Fluid Mech. 123, 459–476.CrossRefGoogle Scholar
Turner, R.E.L. & Vanden-Broeck, J.-M. 1988 Broadening of interfacial solitary waves. Phys. Fluids 31 (9), 2486–2490.CrossRefGoogle Scholar
Wilton, J.R. 1915 On ripples. Phil. Mag. 29 (173), 688–700.CrossRefGoogle Scholar
Yih, C.-S. 2012 Stratified Flows. Elsevier.Google Scholar