Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-17T02:29:30.073Z Has data issue: false hasContentIssue false
  • English
  • Français

Solidification of binary aqueous solutions under periodic cooling. Part 1. Dynamics of mushy-layer growth

Published online by Cambridge University Press:  07 May 2019

Guang-Yu Ding ,
Andrew J. Wells Open the ORCID record for Andrew J. Wells [Opens in a new window]  and
Jin-Qiang Zhong Open the ORCID record for Jin-Qiang Zhong [Opens in a new window]
Guang-Yu Ding
Affiliation:
School of Physics Science and Engineering, Tongji University, Shanghai 200092, China Department of Physics, Chinese University of Hong Kong, Hong Kong, China
Andrew J. Wells
Affiliation:
Department of Physics, University of Oxford, Oxford OX1 3PU, UK
Jin-Qiang Zhong*
Affiliation:
School of Physics Science and Engineering, Tongji University, Shanghai 200092, China
*
†Email address for correspondence: jinqiang@tongji.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We present studies of the solidification of binary aqueous solutions that undergo time-periodic cooling from below. We develop an experiment for solidification of aqueous 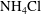$\text{NH}_{4}\text{Cl}$ solutions, where the temperature of the cooling boundary is modulated as a simple periodic function of time with independent variations of the modulation amplitude and frequency. The thickness of the mushy layer exhibits oscillations about the background growth obtained for constant cooling. We consider the deviation given by the difference between states with modulated and fixed cooling, which increases when the modulation amplitude increases but decreases with increasing modulation frequency. At early times, the deviation amplitude is consistent with a scaling argument for growth with quasi-steady modulation. In situ measurements of the mush temperature reveal thermal waves propagating through the mushy layer, with amplitude decaying with height within the mushy layer, whilst the phase lag behind the cooling boundary increases with height. This also leads to phase lags in the variation of the mushy-layer thickness compared to the boundary cooling. There is an asymmetry of the deviation of mushy-layer thickness: during a positive modulation (where the boundary temperature increases at the start of a cycle) the peak thickness deviation has a greater magnitude than the troughs in a negative modulation mode (where the boundary temperature decreases at the start of the cycle). A numerical model is formulated to describe mushy-layer growth with constant bulk concentration and turbulent heat transport at the mush–liquid interface driven by compositional convection associated with a finite interfacial solid fraction. The model recovers key features of the experimental results at early times, including the propagation of thermal waves and oscillations in mushy-layer thickness, although tends to overpredict the mean thickness.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection in porous media Phase change: Solidification/melting
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 121 - 146
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bergman, M. I. & Fearn, D. R. 1994 Chimneys on the Earth’s inner-outer core boundary? Geophys. Res. Lett. 21, 477–480.Google Scholar
Brent, A. D., Voller, V. R. & Reid, K. J. 1988 Enthalpy-porosity technique for modeling convection-diffusion phase change: application to the melting of a pure metal. Numer. Heat Transfer 13, 297–318.Google Scholar
Carslaw, H. S. & Jaeger, J. C. 1959 Conduction of Heat in Solids, 2nd edn. Oxford University Press.Google Scholar
Chalmers, B. 1964 Principles of Solidification. Wiley.Google Scholar
Conte, S. D. & Boor, C. W. D. 1989 Elementary Numerical Analysis: An Algorithmic Approach, 3rd edn. McGraw-Hill Higher Education.Google Scholar
Ding, G. Y., Wells, A. J. & Zhong, J.-Q. 2019 Solidification of binary aqueous solutions under periodic cooling. Part 2. Distribution of solid fraction. J. Fluid Mech. 870, 147–174.Google Scholar
Feltham, D. L., Untersteiner, N., Wettlaufer, J. S. & Worster, M. G. 2006 Sea ice is a mushy layer. Geophys. Res. Lett. 33, L14501.Google Scholar
Fowler, A. C. 1985 The formation of freckles in binary alloys. IMA J. Appl. Maths 35, 159–174.Google Scholar
Hills, R. N., Loper, D. E. & Roberts, P. H. 1983 A thermodynamically consistent model of a mushy zone. Q. J. Mech. Appl. Maths 36, 505–539.Google Scholar
Huguet, L., Alboussiere, T., Bergman, M. I., Deguen, R., Labrosse, S. & Lesceur, G. 2016 Structure of a mushy layer under hypergravity with implications for earth’s inner core. Geophys. J. Intl 204, 1729–1755.Google Scholar
Hunke, E. C., Notz, D., Turner, A. K. & Vancoppenolle, M. 2011 The multiphase physics of sea ice: a review for model developers. Cryosphere 5 (4), 989–1009.Google Scholar
Huppert, H. E. & Worster, M. G. 1985 Dynamic solidification of a binary melt. Nature 314, 703–707.Google Scholar
Katz, R. & Worster, M. 2008 Simulation of directional solidification, thermochemical convection, and chimney formation in a Hele–Shaw cell. Comput. Phys. 227 (23), 9823–9840.Google Scholar
Kerr, R. C., Woods, A. W., Worster, M. G. & Huppert, H. E. 1990a Solidification of an alloy cooled from above. Part 2. Non-equilibrium interfacial kinetics. J. Fluid Mech. 217, 331–348.Google Scholar
Kerr, R. C., Worster, M. G., Woods, A. W. & Huppert, H. E. 1990b Solidification of an alloy cooled from above. Part 1. Equilibrium growth. J. Fluid Mech. 216, 323–342.Google Scholar
Le Bars, M. & Worster, M. G. 2006 Interfacial conditions between a pure fluid and a porous medium: implications for binary alloy solidification. J. Fluid Mech. 550, 149–173.Google Scholar
Neufeld, J. A. & Wettlaufer, J. S. 2008 An experimental study of shear-enhanced convection in a mushy layer. J. Fluid Mech. 612, 363–385.Google Scholar
Notz, D. & Worster, M. G. 2006 A one-dimensional enthalpy model of sea ice. Ann. Glaciol. 44, 123–128.Google Scholar
Notz, D. & Worster, M. G. 2008 In situ measurements of the evolution of young sea ice. J. Geophys. Res. 113 (C3), C03001.Google Scholar
Notz, D. & Worster, M. G. 2009 Desalination processes of sea ice revisited. J. Geophys. Res. 114 (C5), C05006.Google Scholar
Peppin, S. S. L., Aussillous, P., Huppert, H. E. & Worster, M. G. 2007 Steady-state mushy layers: experiments and theory. J. Fluid Mech. 570, 69–77.Google Scholar
Peppin, S. S. L., Huppert, H. E. & Worster, M. G. 2008 Steady-state solidification of aqueous ammonium chloride. J. Fluid Mech. 599, 465–476.Google Scholar
Rees Jones, D. W. & Worster, M. G. 2014 A physically based parameterization of gravity drainage for sea-ice modeling. J. Geophys. Res. Oceans 119 (9), 5599–5621.Google Scholar
Rizwan-Uddin 1999 A nodal method for phase change moving boundary problem. Intl J. Comput. Fluid Dyn. 11, 211–221.Google Scholar
Savović, S. & Caldwell, J. 2003 Finite difference solution of one-dimensional Stefan problem with periodic boundary conditions. Intl J. Heat Mass Transfer 46, 2911–2916.Google Scholar
Schulze, T. P. & Worster, M. G. 1999 Weak convection, liquid inclusions and the formation of chimneys in mushy layers. J. Fluid Mech. 388, 197–215.Google Scholar
Solomon, T. H. & Hartley, R. R. 1998 Measurements of the temperature field of mushy and liquid regions during solidification of aqueous ammonium chloride. J. Fluid Mech. 358, 87–106.Google Scholar
Tait, S. & Jaupart, C. 1989 Compositional convection in viscous melts. Nature 338 (6216), 571–574.Google Scholar
Tait, S. & Jaupart, C. 1992 Compositional convection in a reactive crystalline mush and melt differentiation. J. Geophys. Res. Oceans 97, 6735–6756.Google Scholar
Turner, A. K., Hunke, E. C. & Bitz, C. M. 2013 Two modes of sea-ice gravity drainage: a parameterization for large-scale modeling. J. Geophys. Res. Oceans 118, 2279–2294.Google Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
US National Research Council 2003 International Critical Tables of Numerical Data, Physics, Chemistry, and Technology, Norwich, New York.Google Scholar
Wells, A. J., Wettlaufer, J. S. & Orszag, S. A. 2013 Nonlinear mushy-layer convection with chimneys: stability and optimal solute fluxes. J. Fluid Mech. 716, 203–227.Google Scholar
Wettlaufer, J. S., Worster, M. G. & Huppert, H. E. 1997 Natural convection during solidification of an alloy from above with application to the evolution of sea ice. J. Fluid Mech. 344, 291–316.Google Scholar
Wettlaufer, J. S., Worster, M. G. & Huppert, H. E. 2000 Solidification of leads: theory, experiment, and field observations. J. Geophys. Res. 105, 1123–1134.Google Scholar
Woods, A. W. & Huppert, H. E. 1989 The growth of compositionally stratified solid above a horizontal boundary. J. Fluid Mech. 199, 29–53.Google Scholar
Worster, M. G. 1986 Solidification of an alloy from a cooled boundary. J. Fluid Mech. 167, 481–501.Google Scholar
Worster, M. G. 1997 Convection in mushy layers. Annu. Rev. Fluid Mech. 29, 91–122.Google Scholar
Worster, M. G. 2000 Perspectives in Fluid Dynamics: A Collective Introduction to Current Research. pp. 393–446. Cambridge University Press.Google Scholar
Worster, M. G. & Kerr, R. C. 1994 The transient behaviour of alloys solidified from below prior to the formation of chimneys. J. Fluid Mech. 269, 23–44.Google Scholar
Yang, Y., Verzicco, R. & Lohse, D. 2016 Scaling laws and flow structures of double diffusive convection in the finger regime. J. Fluid Mech. 802, 667–689.Google Scholar
Yao, L. S. & Prusa, J. 1989 Melting and freezing. Adv. Heat Transfer 19, 1–95.Google Scholar
Zhong, J.-Q., Fragoso, A. T., Wells, A. J. & Wettlaufer, J. S. 2012 Finite-sample-size effects on convection in mushy layers. J. Fluid Mech. 704 (2), 89–108.Google Scholar

Ding et al. supplementary movie

Shadowgraphy movies that show the growth of mushy layers and the flows in the liquid region in three modulation modes with Φ0=0 (left), constant cooling (middle) and Φ0=π (right). Results for A=15K, τ=4000s. The movies display 400 times faster than the real time.

Download Ding et al. supplementary movie(Video)
Video 63 MB