Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-05-30T09:07:25.260Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatial evolution of the turbulent/turbulent interface geometry in a cylinder wake

Published online by Cambridge University Press:  10 August 2023

Jiangang Chen Open the ORCID record for Jiangang Chen [Opens in a new window]  and
Oliver R.H. Buxton Open the ORCID record for Oliver R.H. Buxton [Opens in a new window]
Jiangang Chen
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
Oliver R.H. Buxton*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
*
†Email address for correspondence: o.buxton@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

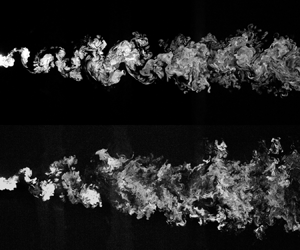
This study aims to examine the spatial evolution of the geometrical features of the turbulent/turbulent interface (TTI) in a cylinder wake. The wake is exposed to various turbulent backgrounds in which the turbulence intensity and the integral length scale are varied independently, and comparisons to a turbulent/non-turbulent interface (TNTI) are drawn. The turbulent wake was marked with a high Schmidt number ($Sc$) scalar, and a planar laser induced fluorescence experiment was carried out to capture the interface between the wake and the ambient flow from $x/d = 5$ to 40, where $x$ is the streamwise coordinate from the centre of the cylinder, and $d$ is the cylinder's diameter. It is found that the TTI generally spreads faster towards the ambient flow than the TNTI. A transition region of the interfaces’ spreading is found at $x/d \approx 15$, after which the interfaces propagate at a slower rate than previously (upstream), and the mean interface positions of both the TNTI and TTI scale with the local wake half-width. The locations of both the TNTI and TTI have non-Gaussian probability density functions (PDFs) in the near wake because of the influence of the large-scale coherent motions present within the flow. Further downstream, after the large-scale coherent motions have dissipated, the TNTI position PDF does become Gaussian. For the first time, we explore the spatial variation of the ‘roughness’ of the TTI, quantified via the fractal dimension, from near field to far field. The length scale in the background flow has a profound effect on the TTI fractal dimension in the near wake, whilst the turbulence intensity becomes important only for the fractal dimension farther downstream.

JFM classification

Mixing: Turbulent mixing Turbulent Flows: Intermittency Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 969 , 25 August 2023 , A4
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abreu, H., Pinho, F.T. & da Silva, C.B. 2022 Turbulent entrainment in viscoelastic fluids. J. Fluid Mech. 934, A36.CrossRefGoogle Scholar
Baj, P., Bruce, P.J.K. & Buxton, O.R.H. 2016 On a PLIF quantification methodology in a nonlinear dye response regime. Exp. Fluids 57 (6), 1–19.CrossRefGoogle Scholar
Ball, C.G., Fellouah, H. & Pollard, A. 2012 The flow field in turbulent round free jets. Prog. Aerosp. Sci. 50, 1–26.CrossRefGoogle Scholar
Bisset, D.K., Hunt, J.C.R. & Rogers, M.M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
Buxton, O.R.H., Breda, M. & Dhall, K. 2019 Importance of small-scale anisotropy in the turbulent/nonturbulent interface region of turbulent free shear flows. Phys. Rev. Fluids 4 (3), 034603.CrossRefGoogle Scholar
Chen, J.G., Zhou, Y., Zhou, T.M. & Antonia, R.A. 2016 Three-dimensional vorticity, momentum and heat transport in a turbulent cylinder wake. J. Fluid Mech. 809, 135–167.CrossRefGoogle Scholar
Cimarelli, A. & Boga, G. 2021 Numerical experiments on turbulent entrainment and mixing of scalars. J. Fluid Mech. 927, A34.CrossRefGoogle Scholar
Cimarelli, A., Cocconi, G., Frohnapfel, B. & De Angelis, E. 2015 Spectral enstrophy budget in a shear-less flow with turbulent/non-turbulent interface. Phys. Fluids 27 (12), 125106.CrossRefGoogle Scholar
Corrsin, S. & Kistler, A.L. 1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. 1244.Google Scholar
Crimaldi, J.P. 1997 The effect of photobleaching and velocity fluctuations on single-point LIF measurements. Exp. Fluids 23 (4), 325–330.CrossRefGoogle Scholar
Eames, I., Jonsson, C. & Johnson, P.B. 2011 The growth of a cylinder wake in turbulent flow. J. Turbul. 12, N39.CrossRefGoogle Scholar
Gampert, M., Boschung, J., Hennig, F., Gauding, M. & Peters, N. 2014 The vorticity versus the scalar criterion for the detection of the turbulent/non-turbulent interface. J. Fluid Mech. 750, 578–596.CrossRefGoogle Scholar
Gordeyev, S.V. & Thomas, F.O. 2000 Coherent structure in the turbulent planar jet. Part 1. Extraction of proper orthogonal decomposition eigenmodes and their self-similarity. J. Fluid Mech. 414, 145–194.CrossRefGoogle Scholar
Kankanwadi, K.S. 2022 Turbulent/turbulent entrainment: a detailed examination of entrainment, and the behaviour of the outer interface as affected by background turbulence. PhD thesis, Imperial College London.CrossRefGoogle Scholar
Kankanwadi, K.S. & Buxton, O.R.H. 2020 Turbulent entrainment into a cylinder wake from a turbulent background. J. Fluid Mech. 905, A35.CrossRefGoogle Scholar
Kankanwadi, K.S. & Buxton, O.R.H. 2022 On the physical nature of the turbulent/turbulent interface. J. Fluid Mech. 942, A31.CrossRefGoogle Scholar
Kankanwadi, K.S. & Buxton, O.R.H. 2023 Influence of freestream turbulence on the near-field growth of a turbulent cylinder wake: turbulent entrainment and wake meandering. Phys. Rev. Fluids 8, 034603.CrossRefGoogle Scholar
Kohan, K.F. & Gaskin, S.J. 2022 On the scalar turbulent/turbulent interface of axisymmetric jets. J. Fluid Mech. 950, A32.CrossRefGoogle Scholar
Long, Y., Wang, J. & Pan, C. 2022 Universal modulations of large-scale motions on entrainment of turbulent boundary layers. J. Fluid Mech. 941, A68.CrossRefGoogle Scholar
Matsumura, M. & Antonia, R.A. 1993 Momentum and heat transport in the turbulent intermediate wake of a circular cylinder. J. Fluid Mech. 250, 651–668.CrossRefGoogle Scholar
Mistry, D., Philip, J., Dawson, J.R. & Marusic, I. 2016 Entrainment at multi-scales across the turbulent/non-turbulent interface in an axisymmetric jet. J. Fluid Mech. 802, 690–725.CrossRefGoogle Scholar
Pal, A. & Sarkar, S. 2015 Effect of external turbulence on the evolution of a wake in stratified and unstratified environments. J. Fluid Mech. 772, 361–385.CrossRefGoogle Scholar
Porté-Agel, F., Bastankhah, M. & Shamsoddin, S. 2020 Wind-turbine and wind-farm flows: a review. Boundary-Layer Meteorol. 174 (1), 1–59.CrossRefGoogle ScholarPubMed
Prasad, R.R. & Sreenivasan, K.R. 1989 Scalar interfaces in digital images of turbulent flows. Exp. Fluids 7 (4), 259–264.CrossRefGoogle Scholar
Rehab, H., Antonia, R.A. & Djenidi, L. 2001 Streamwise evolution of a high-Schmidt-number passive scalar in a turbulent plane wake. Exp. Fluids 31 (2), 186–192.CrossRefGoogle Scholar
Rind, E. & Castro, I.P. 2012 a Direct numerical simulation of axisymmetric wakes embedded in turbulence. J. Fluid Mech. 710, 482–504.CrossRefGoogle Scholar
Rind, E. & Castro, I.P. 2012 b On the effects of free-stream turbulence on axisymmetric disc wakes. Exp. Fluids 53, 301–318.CrossRefGoogle Scholar
da Silva, C.B., Hunt, J.C.R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46 (1), 567–590.CrossRefGoogle Scholar
de Silva, C.M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent-nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111 (4), 044501.CrossRefGoogle ScholarPubMed
Silva, T.S. & da Silva, C.B. 2017 The behaviour of the scalar gradient across the turbulent/non-turbulent interface in jets. Phys. Fluids 29 (8), 085106.CrossRefGoogle Scholar
Sreenivasan, K.R. & Meneveau, C. 1986 The fractal facets of turbulence. J. Fluid Mech. 173, 357–386.CrossRefGoogle Scholar
Sreenivasan, K.R., Ramshankar, R. & Meneveau, C.H. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Tennekes, H. & Lumley, J.L. 1972 A First Course in Turbulence. MIT Press.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear flow. Cambridge University Press.Google Scholar
Vanderwel, C. & Tavoularis, S. 2014 On the accuracy of PLIF measurements in slender plumes. Exp. Fluids 55 (8), 1–16.CrossRefGoogle Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2014 Enstrophy and passive scalar transport near the turbulent/non-turbulent interface in a turbulent planar jet flow. Phys. Fluids 26 (10), 105103.CrossRefGoogle Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2015 Turbulent mixing of passive scalar near turbulent and non-turbulent interface in mixing layers. Phys. Fluids 27 (8), 085109.CrossRefGoogle Scholar
Westerweel, J., Fukushima, C., Pedersen, J.M. & Hunt, J.C.R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.CrossRefGoogle Scholar
Wu, Z., Zaki, T.A. & Meneveau, C. 2020 High-Reynolds-number fractal signature of nascent turbulence during transition. Proc. Natl Acad. Sci. 117 (7), 3461–3468.CrossRefGoogle ScholarPubMed
Yule, A.J. 1978 Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 89 (3), 413–432.CrossRefGoogle Scholar
Zhou, T.M., Zhou, Y., Yiu, M.W. & Chua, L.P. 2003 Three-dimensional vorticity in a turbulent cylinder wake. Exp. Fluids 35 (5), 459–471.CrossRefGoogle Scholar
Zhou, Y. & Vassilicos, J.C. 2017 Related self-similar statistics of the turbulent/non-turbulent interface and the turbulence dissipation. J. Fluid Mech. 821, 440–457.CrossRefGoogle Scholar
Zhou, Y., Zhang, H.J. & Yiu, M.W. 2002 The turbulent wake of two side-by-side circular cylinders. J. Fluid Mech. 458, 303–332.CrossRefGoogle Scholar