Hostname: page-component-848d4c4894-x24gv Total loading time: 0 Render date: 2024-06-03T01:57:19.230Z Has data issue: false hasContentIssue false
  • English
  • Français

Unified gas-kinetic wave–particle method for polydisperse gas–solid particle multiphase flow

Published online by Cambridge University Press:  21 March 2024

Xiaojian Yang Open the ORCID record for Xiaojian Yang [Opens in a new window] ,
Wei Shyy  and
Kun Xu Open the ORCID record for Kun Xu [Opens in a new window]
Xiaojian Yang
Affiliation:
Department of Mechanical and Aerospace Engineering, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, PR China
Wei Shyy
Affiliation:
Department of Mechanical and Aerospace Engineering, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, PR China
Kun Xu*
Affiliation:
Department of Mechanical and Aerospace Engineering, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, PR China Department of Mathematics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong, PR China Shenzhen Research Institute, Hong Kong University of Science and Technology, Shenzhen 518057, PR China
*
†Email address for correspondence: makxu@ust.hk
Get access Rights & Permissions [Opens in a new window]

Abstract

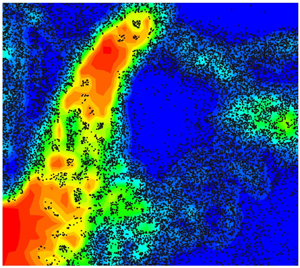
The gas-particle flow with multiple dispersed solid phases is associated with a complicated multiphase flow dynamics. In this paper, a unified algorithm is proposed for the gas-particle multiphase flow. The gas-kinetic scheme (GKS) is used to simulate the gas phase and the multiscale unified gas-kinetic wave–particle (UGKWP) method is developed for the multiple dispersed solid particle phase. For each disperse solid particle phase, the decomposition of deterministic wave and statistic particle in UGKWP is based on the local cell's Knudsen number. The method for solid particle phase can become the Eulerian fluid approach at the small cell's Knudsen number and the Lagrangian particle approach at the large cell's Knudsen number. This becomes an optimized algorithm for simulating dispersed particle phases with a large variation of Knudsen numbers due to different physical properties of the individual particle phase, such as the particle diameter, material density, etc. The GKS-UGKWP method for gas-particle flow unifies the Eulerian–Eulerian and Eulerian–Lagrangian methods. The particle and wave decompositions for the solid particle phase and their coupled evolution in UGKWP come from the consideration to balance the physical accuracy and numerical efficiency. Two cases of a gas–solid fluidization system, i.e. one circulating fluidized bed and one turbulent fluidized bed, are simulated. The typical flow structures of the fluidized particles are captured, and the time-averaged variables of the flow field agree well with the experimental measurements. In addition, the shock particle–bed interaction is studied by the proposed method, which validates the algorithm for the polydisperse gas-particle system in the highly compressible case, where the dynamic evolution process of the particle cloud is investigated.

JFM classification

Compressible Flows: Shock waves Multiphase and Particle-laden Flows: Fluidized beds Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 983 , 25 March 2024 , A37
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benyahia, S. 2022 Selecting the best approach for fluidized bed simulation of aeratable particles. Powder Technol. 399, 117178.CrossRefGoogle Scholar
Cello, F., Di Renzo, A. & Di Maio, F.P. 2010 A semi-empirical model for the drag force and fluid-particle interaction in polydisperse suspensions. Chem. Engng Sci. 65 (10), 3128–3139.CrossRefGoogle Scholar
Ceresiat, L., Kolehmainen, J. & Ozel, A. 2021 Charge transport equation for bidisperse collisional granular flows with non-equipartitioned fluctuating kinetic energy. J. Fluid Mech. 926, A35.CrossRefGoogle Scholar
Chen, X., Wang, J. & Li, J. 2013 Coarse grid simulation of heterogeneous gas-solid flow in a CFB riser with polydisperse particles. Chem. Engng J. 234, 173–183.CrossRefGoogle Scholar
Clift, R. 1970 The motion of particles in turbulent gas streams. Proc. Chemeca 1, 14.Google Scholar
Dou, J., Wang, L., Ge, W. & Ouyang, J. 2023 Effect of mesoscale structures on solid phase stress in gas-solid flows. Chem. Engng J. 455, 140825.CrossRefGoogle Scholar
Fan, R. & Fox, R.O. 2008 Segregation in polydisperse fluidized beds: validation of a multi-fluid model. Chem. Engng Sci. 63 (1), 272–285.CrossRefGoogle Scholar
Feng, Y.Q, Xu, B.H., Zhang, S.J., Yu, A.B. & Zulli, P. 2004 Discrete particle simulation of gas fluidization of particle mixtures. AIChE J. 50 (8), 1713–1728.CrossRefGoogle Scholar
Fox, R.O. & Vedula, P. 2010 Quadrature-based moment model for moderately dense polydisperse gas-particle flows. Ind. Engng Chem. Res. 49 (11), 5174–5187.CrossRefGoogle Scholar
Gao, J., Lan, X., Fan, Y., Chang, J., Wang, G., Lu, C. & Xu, C. 2009 Hydrodynamics of gas-solid fluidized bed of disparately sized binary particles. Chem. Engng Sci. 64 (20), 4302–4316.CrossRefGoogle Scholar
Gibilaro, L.G., Di Felice, R., Waldram, S.P. & Foscolo, P.U. 1985 Generalized friction factor and drag coefficient correlations for fluid-particle interactions. Chem. Engng Sci. 40 (10), 1817–1823.CrossRefGoogle Scholar
Gidaspow, D. 1994 Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions. Academic Press.Google Scholar
He, Y., Zhao, H., Wang, H. & Zheng, C. 2015 Differentially weighted direct simulation Monte Carlo method for particle collision in gas-solid flows. Particuology 21, 135–145.CrossRefGoogle Scholar
Houim, R.W. & Oran, E.S. 2016 A multiphase model for compressible granular-gaseous flows: formulation and initial tests. J. Fluid Mech. 789, 166–220.CrossRefGoogle Scholar
Ishii, M. & Hibiki, T. 2006 Thermo-Fluid Dynamics of Two-Phase Flow. Springer Science & Business Media.CrossRefGoogle Scholar
Johnson, P.C. & Jackson, R. 1987 Frictional-collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 176, 67–93.CrossRefGoogle Scholar
Lei, H., Zhu, L. & Luo, Z. 2023 Study of fluid cell coarsening for CFD-DEM simulations of polydisperse gas-solid flows. Particuology 73, 128–138.CrossRefGoogle Scholar
Li, J. & Kwauk, M. 1994 Particle-Fluid Two-Phase Flow: The Energy-Minimization Multi-Scale method. Metallurgical Industry Press.Google Scholar
Li, P., Lan, X., Xu, C., Wang, G., Lu, C. & Gao, J. 2009 Drag models for simulating gas-solid flow in the turbulent fluidization of FCC particles. Particuology 7 (4), 269–277.CrossRefGoogle Scholar
Ling, Y., Wagner, J.L., Beresh, S.J., Kearney, S.P. & Balachandar, S. 2012 Interaction of a planar shock wave with a dense particle curtain: modeling and experiments. Phys. Fluids 24 (11), 113301.CrossRefGoogle Scholar
Liu, C., Wang, Z. & Xu, K. 2019 A unified gas-kinetic scheme for continuum and rarefied flows VI: dilute disperse gas-particle multiphase system. J. Comput. Phys. 386, 264–295.CrossRefGoogle Scholar
Liu, C. & Xu, K. 2017 A unified gas kinetic scheme for continuum and rarefied flows V: multiscale and multi-component plasma transport. Commun. Comput. Phys. 22 (5), 1175–1223.CrossRefGoogle Scholar
Liu, C., Zhu, Y. & Xu, K. 2020 Unified gas-kinetic wave-particle methods I: continuum and rarefied gas flow. J. Comput. Phys. 401, 108977.CrossRefGoogle Scholar
Lu, H. & Gidaspow, D. 2003 Hydrodynamics of binary fluidization in a riser: CFD simulation using two granular temperatures. Chem. Engng Sci. 58 (16), 3777–3792.Google Scholar
Marchisio, D.L. & Fox, R.O. 2013 Computational Models for Polydisperse Particulate and Multiphase Systems. Cambridge University Press.CrossRefGoogle Scholar
Mathiesen, V., Solberg, T., Arastoopour, H. & Hjertager, B.H. 1999 Experimental and computational study of multiphase gas/particle flow in a CFB riser. AIChE J. 45 (12), 2503–2518.CrossRefGoogle Scholar
Mckeen, T. & Pugsley, T. 2003 Simulation and experimental validation of a freely bubbling bed of FCC catalyst. Powder Technol. 129 (1-3), 139–152.CrossRefGoogle Scholar
Niemi, T.J. 2012 Particle size distribution in CFD simulation of gas-particle flows. Master's thesis, Aalto University, Finland.Google Scholar
Parmar, M., Haselbacher, A. & Balachandar, S. 2008 On the unsteady inviscid force on cylinders and spheres in subcritical compressible flow. Phil. Trans. R. Soc. A 366 (1873), 2161–2175.CrossRefGoogle ScholarPubMed
Passalacqua, A., Fox, R.O., Garg, R. & Subramaniam, S. 2010 A fully coupled quadrature-based moment method for dilute to moderately dilute fluid–particle flows. Chem. Engng Sci. 65 (7), 2267–2283.CrossRefGoogle Scholar
Qin, Z., Zhou, Q. & Wang, J. 2019 An EMMS drag model for coarse grid simulation of polydisperse gas-solid flow in circulating fluidized bed risers. Chem. Engng Sci. 207, 358–378.CrossRefGoogle Scholar
Rong, L.W., Dong, K.J. & Yu, A.B. 2014 Lattice–Boltzmann simulation of fluid flow through packed beds of spheres: effect of particle size distribution. Chem. Engng Sci. 116, 508–523.CrossRefGoogle Scholar
Saurel, R. & Abgrall, R. 1999 A multiphase Godunov method for compressible multifluid and multiphase flows. J. Comput. Phys. 150 (2), 425–467.CrossRefGoogle Scholar
Snider, D.M. 2001 An incompressible three-dimensional multiphase particle-in-cell model for dense particle flows. J. Comput. Phys. 170 (2), 523–549.CrossRefGoogle Scholar
Snider, D.M. 2007 Three fundamental granular flow experiments and CPFD predictions. Powder Technol. 176 (1), 36–46.CrossRefGoogle Scholar
Sun, W., Jiang, S. & Xu, K. 2015 An asymptotic preserving unified gas kinetic scheme for gray radiative transfer equations. J. Comput. Phys. 285, 265–279.CrossRefGoogle Scholar
Syamlal, M. 1987 The particle-particle drag term in a multiparticle model of fluidization. Tech. Rep. EG and G Washington Analytical Services Center, Inc., Morgantown, WV, USA.Google Scholar
Tian, B., Zeng, J., Meng, B., Chen, Q., Guo, X. & Xue, K. 2020 Compressible multiphase particle-in-cell method (CMP-PIC) for full pattern flows of gas-particle system. J. Comput. Phys. 418, 109602.CrossRefGoogle Scholar
Toro, E.F. 2013 Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction. Springer Science & Business Media.Google Scholar
Tsuji, Y., Kawaguchi, T. & Tanaka, T. 1993 Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 77 (1), 79–87.CrossRefGoogle Scholar
Verma, V. & Padding, J.T. 2020 A novel approach to MP-PIC: continuum particle model for dense particle flows in fluidized beds. Chem. Engng Sci.: X 6, 100053.Google Scholar
Wang, Q., Niemi, T., Peltola, J., Kallio, S., Yang, H., Lu, J. & Wei, L. 2015 Particle size distribution in CPFD modeling of gas-solid flows in a CFB riser. Particuology 21, 107–117.CrossRefGoogle Scholar
Wang, W. & Li, J. 2007 Simulation of gas-solid two-phase flow by a multi-scale CFD approach—of the EMMS model to the sub-grid level. Chem. Engng Sci. 62 (1–2), 208–231.CrossRefGoogle Scholar
Xu, K. 2001 A gas-kinetic BGK scheme for the Navier–Stokes equations and its connection with artificial dissipation and Godunov method. J. Comput. Phys. 171 (1), 289–335.CrossRefGoogle Scholar
Xu, K. 2021 A Unified Computational Fluid Dynamics Framework from Rarefied to Continuum Regimes. Elements in Aerospace Engineering, Cambidge University Press.CrossRefGoogle Scholar
Xu, K. & Huang, J.-C. 2010 A unified gas-kinetic scheme for continuum and rarefied flows. J. Comput. Phys. 229 (20), 7747–7764.CrossRefGoogle Scholar
Yan, W.-C., Dong, T., Zhou, Y.-N. & Luo, Z.-H. 2023 Computational modeling toward full chain of polypropylene production: from molecular to industrial scale. Chem. Engng Sci. 269, 118448.CrossRefGoogle Scholar
Yang, N., Wang, W., Ge, W. & Li, J. 2003 CFD simulation of concurrent-up gas-solid flow in circulating fluidized beds with structure-dependent drag coefficient. Chem. Engng J. 96 (1–3), 71–80.CrossRefGoogle Scholar
Yang, X., Ji, X., Shyy, W. & Xu, K. 2022 a Comparison of the performance of high-order schemes based on the gas-kinetic and HLLC fluxes. J. Comput. Phys. 448, 110706.CrossRefGoogle Scholar
Yang, X., Liu, C., Ji, X., Shyy, W. & Xu, K. 2022 b Unified gas-kinetic wave-particle methods VI: disperse dilute gas-particle multiphase flow. Commun. Comput. Phys. 31 (3), 669–706.CrossRefGoogle Scholar
Yang, X., Shyy, W. & Xu, K. 2022 c Unified gas-kinetic wave-particle method for gas-particle two-phase flow from dilute to dense solid particle limit. Phys. Fluids 34 (2), 023312.CrossRefGoogle Scholar
Yang, X., Wei, Y., Shyy, W. & Xu, K. 2023 Unified gas-kinetic wave-particle method for three-dimensional simulation of gas-particle fluidized bed. Chem. Engng J. 453, 139541.CrossRefGoogle Scholar
Zhang, Q., Wang, S., Lu, H., Liu, G., Wang, S. & Zhao, G. 2017 a A coupled Eulerian fluid phase-Eulerian solids phase-Lagrangian discrete particles hybrid model applied to gas-solids bubbling fluidized beds. Powder Technol. 315, 385–397.Google Scholar
Zhang, Y., Xu, J., Chang, Q., Zhao, P., Wang, J. & Ge, W. 2023 Numerical simulation of fluidization: driven by challenges. Powder Technol. 414, 118092.CrossRefGoogle Scholar
Zhang, Y., Zhao, Y., Lu, L., Ge, W., Wang, J. & Duan, C. 2017 b Assessment of polydisperse drag models for the size segregation in a bubbling fluidized bed using discrete particle method. Chem. Engng Sci. 160, 106–112.CrossRefGoogle Scholar
Zhao, B. & Wang, J. 2021 Kinetic theory of polydisperse gas-solid flow: Navier–Stokes transport coefficients. Phys. Fluids 33 (10), 103322.CrossRefGoogle Scholar
Zhong, W., Yu, A., Zhou, G., Xie, J. & Zhang, H. 2016 CFD simulation of dense particulate reaction system: approaches, recent advances and applications. Chem. Engng Sci. 140, 16–43.CrossRefGoogle Scholar
Zhu, L.-T., Liu, Y.-X., Tang, J.-X. & Luo, Z.-H. 2019 a A material-property-dependent sub-grid drag model for coarse-grained simulation of 3D large-scale CFB risers. Chem. Engng Sci. 204, 228–245.CrossRefGoogle Scholar
Zhu, L.-T., Ouyang, B., Lei, H. & Luo, Z.-H. 2021 Conventional and data-driven modeling of filtered drag, heat transfer, and reaction rate in gas–particle flows. AIChE J. 67 (8), e17299.CrossRefGoogle Scholar
Zhu, Y., Liu, C., Zhong, C. & Xu, K. 2019 b Unified gas-kinetic wave-particle methods II. Multiscale simulation on unstructured mesh. Phys. Fluids 31 (6), 067105.CrossRefGoogle Scholar