Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-01T04:04:41.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscous flows in a muddy seabed induced by a solitary wave

Published online by Cambridge University Press:  25 February 2008

YONG SUNG PARK ,
PHILIP L.-F. LIU  and
STEPHEN J. CLARK
YONG SUNG PARK
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
PHILIP L.-F. LIU
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA Institute of Hydrological and Oceanic Sciences, National Central University, Jhongli, Taiwan
STEPHEN J. CLARK
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Liu & Chan (J. Fluid Mech. vol. 579, 2007, p. 467, hereinafter referred to as LC) derived analytical solutions for the interactions between shallow water waves and a viscous fluid seabed. In this paper we present a set of new experimental data on the solitary-wave-induced flows in a viscous muddy seabed so as to validate LC's theory and the approximations employed. In the experiments a clear silicone fluid was used as the viscous mud and particle image velocimetry was employed to measure the velocity field inside the viscous mud. The shear stress along the bottom of the mud bed and the displacement of the water--mud interface were also deduced from data. Experimental results showed excellent agreement with the theoretical solutions. Additional analyses were performed to show that the ratio of the muddy seabed thickness to the corresponding bottom boundary-layer thickness, 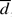, plays an important role in characterizing mud flow regimes. When 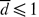, the vertical profile of the horizontal velocity in the mud bed can be parameterized as a parabola. On the other hand, when 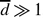, the velocity profile appears as a plug flow above a thin viscous layer. When 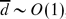, the flow patterns are more complex than the other two regimes and flow reversal can occur inside the viscous mud bed.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 598 , 10 March 2008 , pp. 383 - 392
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Dalrymple, R. A. & Liu, P. L.-F. 1978 Waves over soft mud: a two-layer fluid model. J. Phys. Oceanogr. 8, 1121–1131.2.0.CO;2>CrossRefGoogle Scholar
Foda, M. A. 1989 Sideband damping of water waves over a soft bed. J. Fluid Mech. 201, 189–201.CrossRefGoogle Scholar
Gade, H. G. 1958 Effects of non-rigid, impermeable bottom on plane surface waves in shallow water. J. Mar. Res. 16, 61–82.Google Scholar
Grimshaw, R. 1971 The solitary wave in water of variable depth. Part 2. J. Fluid Mech. 46, 611–622.CrossRefGoogle Scholar
Liu, P. L.-F. 1973 Damping of water waves over porous bed. J. Hydraul. Div. ASCE 99, 2263–2271.CrossRefGoogle Scholar
Liu, P. L.-F. & Chan, I.-C. 2007 On long wave propagation over a fluid-mud seabed. J. Fluid Mech. 579, 467–480.CrossRefGoogle Scholar
Liu, P. L.-F. & Orfila, A. 2004 Viscous effects on transient long-wave propagation. J. Fluid Mech. 520, 83–92.CrossRefGoogle Scholar
Liu, P. L.-F., Park, Y. S. & Cowen, E. A. 2007 a Boundary layer flow and bed shear stress under a solitary wave. J. Fluid Mech. 574, 449–463.CrossRefGoogle Scholar
Liu, P. L.-F., Park, Y. S. & Lara, J. L. 2007 b Long-wave-induced flows in an unsaturated permeable seabed. J. Fluid Mech. 586, 323–345.CrossRefGoogle Scholar
MacPherson, H. 1980 The attenuation of water waves over a non-rigid bed. J. Fluid Mech. 97, 721–742.CrossRefGoogle Scholar
Wen, J. & Liu, P. L.-F. 1995 Mass transport in water waves over an elastic bed. Proc. R. Soc. Lond. A 450, 371–390.Google Scholar
Yamamoto, T., Koning, H. L., Sellmeijer, H. & Hijum, E. V. 1978 On the response of a poro-elastic bed to water waves. J. Fluid Mech. 87, 193–206.CrossRefGoogle Scholar