Hostname: page-component-848d4c4894-75dct Total loading time: 0 Render date: 2024-05-27T23:44:44.738Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex line entanglement in active Beltrami flows

Published online by Cambridge University Press:  01 March 2024

Nicolas Romeo Open the ORCID record for Nicolas Romeo [Opens in a new window] ,
Jonasz Słomka Open the ORCID record for Jonasz Słomka [Opens in a new window] ,
Jörn Dunkel Open the ORCID record for Jörn Dunkel [Opens in a new window]  and
Keaton J. Burns Open the ORCID record for Keaton J. Burns [Opens in a new window]
Nicolas Romeo
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA Department of Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Jonasz Słomka
Affiliation:
Institute of Environmental Engineering, ETH Zürich, Zurich 8092, Switzerland
Jörn Dunkel
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Keaton J. Burns*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA Center for Computational Astrophysics, Flatiron Institute, New York, NY 10010, USA
*
†Email address for correspondence: kjburns@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

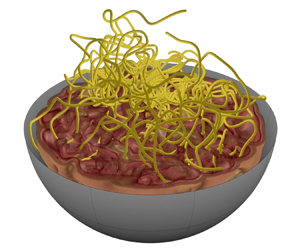
Over the last decade, substantial progress has been made in understanding the topology of quasi-two-dimensional (2-D) non-equilibrium fluid flows driven by ATP-powered microtubules and microorganisms. By contrast, the topology of three-dimensional (3-D) active fluid flows still poses interesting open questions. Here, we study the topology of a spherically confined active flow using 3-D direct numerical simulations of generalized Navier–Stokes (GNS) equations at the scale of typical microfluidic experiments. Consistent with earlier results for unbounded periodic domains, our simulations confirm the formation of Beltrami-like bulk flows with spontaneously broken chiral symmetry in this model. Furthermore, by leveraging fast methods to compute linking numbers, we explicitly connect this chiral symmetry breaking to the entanglement statistics of vortex lines. We observe that the mean of linking number distribution converges to the global helicity, consistent with the asymptotic result by Arnold [In Vladimir I. Arnold – Collected Works (ed. A.B. Givental, B.A. Khesin, A.N. Varchenko, V.A. Vassiliev & O.Y. Viro), pp. 357–375. Springer]. Additionally, we characterize the rate of convergence of this measure with respect to the number and length of observed vortex lines, and examine higher moments of the distribution. We find that the full distribution is well described by a k-Gamma distribution, in agreement with an entropic argument. Beyond active suspensions, the tools for the topological characterization of 3-D vector fields developed here are applicable to any solenoidal field whose curl is tangent to or cancels at the boundaries of a simply connected domain.

JFM classification

Complex Fluids: Active matter Mathematical Foundations: Topological fluid dynamics Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 982 , 10 March 2024 , A12
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alert, R., Casademunt, J. & Joanny, J.-F. 2022 Active turbulence. Annu. Rev. Condens. Matt. Phys. 13 (1), 143–170.CrossRefGoogle Scholar
Arnold, V.I. 1974 The asymptotic Hopf invariant and its applications. In Vladimir I. Arnold – Collected Works (ed. A.B. Givental, B.A. Khesin, A.N. Varchenko, V.A. Vassiliev & O.Y. Viro), pp. 357–375. Springer.Google Scholar
Ascher, U.M., Ruuth, S.J. & Spiteri, R.J. 1997 Implicit-explicit Runge–Kutta methods for time-dependent partial differential equations. Appl. Numer. Maths 25 (2–3), 151–167.CrossRefGoogle Scholar
Aste, T. & Di Matteo, T. 2008 Emergence of Gamma distributions in granular materials and packing models. Phys. Rev. E 77 (2), 021309.CrossRefGoogle ScholarPubMed
Aste, T., Di Matteo, T., Saadatfar, M., Senden, T.J., Schröter, M. & Swinney, H.L. 2007 An invariant distribution in static granular media. Europhys. Lett. 79 (2), 24003.Google Scholar
Atia, L., et al. 2018 Geometric constraints during epithelial jamming. Nat. Phys. 14 (6), 613–620.Google Scholar
Bentkamp, L., Drivas, T.D., Lalescu, C.C. & Wilczek, M. 2022 The statistical geometry of material loops in turbulence. Nat. Commun. 13 (1), 2088.Google Scholar
Beresnev, I.A. & Nikolaevskiy, V.N. 1993 A model for nonlinear seismic waves in a medium with instability. Physica D 66 (1), 1–6.CrossRefGoogle Scholar
Berger, M.A. & Field, G.B. 1984 The topological properties of magnetic helicity. J. Fluid Mech. 147, 133–148.Google Scholar
Bi, D., Henkes, S., Daniels, K.E. & Chakraborty, B. 2015 The statistical physics of athermal materials. Annu. Rev. Condens. Matt. Phys. 6 (1), 63–83.Google Scholar
Biferale, L., Musacchio, S. & Toschi, F. 2012 Inverse energy cascade in three-dimensional isotropic turbulence. Phys. Rev. Lett. 108 (16), 164501.CrossRefGoogle ScholarPubMed
Binysh, J., Kos, Ž., Čopar, S., Ravnik, M. & Alexander, G.P. 2020 Three-dimensional active defect loops. Phys. Rev. Lett. 124 (8), 088001.Google Scholar
Boffetta, G. & Ecke, R.E. 2012 Two-dimensional turbulence. Annu. Rev. Fluid Mech. 44 (1), 427–451.Google Scholar
Boullé, N., Słomka, J. & Townsend, A. 2021 An optimal complexity spectral method for Navier–Stokes simulations in the ball. Preprint arXiv:2103.16638.Google Scholar
Bricard, A., Caussin, J.-B., Desreumaux, N., Dauchot, O. & Bartolo, D. 2013 Emergence of macroscopic directed motion in populations of motile colloids. Nature 503 (7474), 95–98.Google Scholar
Burns, K.J., Vasil, G.M., Oishi, J.S., Lecoanet, D. & Brown, B.P. 2020 Dedalus: a flexible framework for numerical simulations with spectral methods. Phys. Rev. Res. 2 (2), 023068.CrossRefGoogle Scholar
Chardac, A., Hoffmann, L.A., Poupart, Y., Giomi, L. & Bartolo, D. 2021 Topology-driven ordering of flocking matter. Phys. Rev. X 11 (3), 031069.Google Scholar
Čopar, S., Aplinc, J., Kos, Ž., Žumer, S. & Ravnik, M. 2019 Topology of three-dimensional active nematic turbulence confined to droplets. Phys. Rev. X 9 (3), 031051.Google Scholar
Day, T.C., et al. 2022 Cellular organization in lab-evolved and extant multicellular species obeys a maximum entropy law. eLife 11, e72707.CrossRefGoogle ScholarPubMed
Dombre, T., Frisch, U., Greene, J.M., Hénon, M., Mehr, A. & Soward, A.M. 1986 Chaotic streamlines in the abc flows. J. Fluid Mech. 167, 353–391.CrossRefGoogle Scholar
Doostmohammadi, A., Adamer, M.F., Thampi, S.P. & Yeomans, J.M. 2016 Stabilization of active matter by flow-vortex lattices and defect ordering. Nat. Commun. 7 (1), 10557.CrossRefGoogle ScholarPubMed
Drossel, B. & Kardar, M. 1996 Winding angle distributions for random walks and flux lines. Phys. Rev. E 53 (6), 5861–5871.Google Scholar
Du Roure, O., Lindner, A., Nazockdast, E.N. & Shelley, M.J. 2019 Dynamics of flexible fibers in viscous flows and fluids. Annu. Rev. Fluid Mech. 51 (1), 539–572.Google Scholar
Duclos, G.SEP, et al. 2020 Topological structure and dynamics of three-dimensional active nematics. Science 367 (6482), 1120–1124.CrossRefGoogle ScholarPubMed
Dunkel, J., Heidenreich, S., Bär, M. & Goldstein, R.E. 2013 a Minimal continuum theories of structure formation in dense active fluids. New J. Phys. 15 (4), 045016.CrossRefGoogle Scholar
Dunkel, J., Heidenreich, S., Drescher, K., Wensink, H.H., Bär, M. & Goldstein, R.E. 2013 b Fluid dynamics of bacterial turbulence. Phys. Rev. Lett. 110 (22), 228102.CrossRefGoogle ScholarPubMed
Durham, W.M., Climent, E., Barry, M., De Lillo, F., Boffetta, G., Cencini, M. & Stocker, R. 2013 Turbulence drives microscale patches of motile phytoplankton. Nat. Commun. 4 (1), 2148.Google Scholar
Edwards, S.F. & Oakeshott, R.B.S. 1989 Theory of powders. Physica A 157 (3), 1080–1090.CrossRefGoogle Scholar
Eyink, G.L. & Sreenivasan, K.R. 2006 Onsager and the theory of hydrodynamic turbulence. Rev. Mod. Phys. 78 (1), 87–135.Google Scholar
Giomi, L. 2015 Geometry and topology of turbulence in active nematics. Phys. Rev. X 5 (3), 031003.Google Scholar
Hall, P. 1992 Principles of edgeworth expansion. In The Bootstrap and Edgeworth Expansion, Springer Series in Statistics, pp. 39–81. Springer.CrossRefGoogle Scholar
Hänninen, R. & Baggaley, A.W. 2014 Vortex filament method as a tool for computational visualization of quantum turbulence. Proc. Natl Acad. Sci. 111 (Supplement 1), 4667–4674.Google Scholar
Hastings, A., Abbott, K.C., Cuddington, K., Francis, T., Gellner, G., Lai, Y.-C., Morozov, A., Petrovskii, S., Scranton, K. & Zeeman, M.L. 2018 Transient phenomena in ecology. Science 361 (6406), eaat6412.Google Scholar
Hodges, S.E., Munroe, M., Gadomski, W., Cooper, J. & Raymer, M.G. 1997 Turn-on transient dynamics in a multimode, compound-cavity laser. J. Opt. Soc. Am. B 14 (1), 180.Google Scholar
James, M., Bos, W.J.T. & Wilczek, M. 2018 Turbulence and turbulent pattern formation in a minimal model for active fluids. Phys. Rev. Fluids 3 (6), 061101.Google Scholar
Kauffman, L.H. (Ed.) 1995 Knots and applications. Series on Knots and Everything, vol. 6. World Scientific.CrossRefGoogle Scholar
Kirchenbuechler, I., Guu, D., Kurniawan, N.A., Koenderink, G.H. & Lettinga, M.P. 2014 Direct visualization of flow-induced conformational transitions of single actin filaments in entangled solutions. Nat. Commun. 5 (1), 5060.Google Scholar
Kleckner, D. & Irvine, W.T.M. 2013 Creation and dynamics of knotted vortices. Nat. Phys. 9 (4), 253–258.CrossRefGoogle Scholar
Koch, C.-M. & Wilczek, M. 2021 Role of advective inertia in active nematic turbulence. Phys. Rev. Lett. 127 (26), 268005.Google Scholar
Kosterlitz, J.M. & Thouless, D.J. 1973 Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C 6 (7), 1181–1203.CrossRefGoogle Scholar
Kralj, N., Ravnik, M. & Kos, Ž. 2023 Defect line coarsening and refinement in active nematics. Phys. Rev. Lett. 130 (12), 128101.CrossRefGoogle ScholarPubMed
Lakhtakia, A. 1994 Viktor Trkal, Beltrami fields, and Trkalian flows. Czech. J. Phys. 44 (2), 89–96.Google Scholar
Lecoanet, D., Vasil, G.M., Burns, K.J., Brown, B.P. & Oishi, J.S. 2019 Tensor calculus in spherical coordinates using Jacobi polynomials. Part II. Implementation and examples. J. Comput. Phys. 3, 100012.Google Scholar
Linkmann, M., Marchetti, M.C., Boffetta, G. & Eckhardt, B. 2020 Condensate formation and multiscale dynamics in two-dimensional active suspensions. Phys. Rev. E 101 (2), 022609.CrossRefGoogle ScholarPubMed
López, H.M., Gachelin, J., Douarche, C., Auradou, H. & Clément, E. 2015 Turning bacteria suspensions into superfluids. Phys. Rev. Lett. 115 (2), 028301.Google Scholar
Marko, J.F. 2011 Scaling of linking and writhing numbers for spherically confined and topologically equilibrated flexible polymers. J. Stat. Phys. 142 (6), 1353–1370.CrossRefGoogle ScholarPubMed
Matsuzawa, T., Mitchell, N.P., Perrard, S. & Irvine, W.T.M. 2023 Creation of an isolated turbulent blob fed by vortex rings. Nat. Phys. 19, 1193–1200.CrossRefGoogle Scholar
McKeown, R., Ostilla-Mónico, R., Pumir, A., Brenner, M.P. & Rubinstein, S.M. 2020 Turbulence generation through an iterative cascade of the elliptical instability. Sci. Adv. 6 (9), eaaz2717.Google Scholar
Moffatt, H.K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35 (1), 117–129.Google Scholar
Morozov, A., Abbott, K., Cuddington, K., Francis, T., Gellner, G., Hastings, A., Lai, Y.-C., Petrovskii, S., Scranton, K. & Zeeman, M.L. 2020 Long transients in ecology: theory and applications. Phys. Life Rev. 32, 1–40.CrossRefGoogle ScholarPubMed
Nambiar, S., Nott, P.R. & Subramanian, G. 2017 Stress relaxation in a dilute bacterial suspension. J. Fluid Mech. 812, 41–64.CrossRefGoogle Scholar
Onsager, L. 1949 Statistical hydrodynamics. Il Nuovo Cimento 6 (S2), 279–287.CrossRefGoogle Scholar
Orlandini, E. & Whittington, S.G. 2007 Statistical topology of closed curves: some applications in polymer physics. Rev. Mod. Phys. 79 (2), 611–642.Google Scholar
Panagiotou, E. 2019 Topological entanglement and its relation to polymer material properties. In Knots, Low-Dimensional Topology and Applications (ed. C.C. Adams, C.M.A. Gordon, V.F.R. Jones, L.H. Kauffman, S. Lambropoulou, K.C. Millett, J.H. Przytycki, R. Ricca & R. Sazdanovic), Springer Proceedings in Mathematics & Statistics, vol. 284, pp. 435–447. Springer International Publishing.Google Scholar
Panagiotou, E., Millett, K.C. & Lambropoulou, S. 2010 The linking number and the writhe of uniform random walks and polygons in confined spaces. J. Phys. A 43 (4), 045208.Google Scholar
Peng, Y., Liu, Z. & Cheng, X. 2021 Imaging the emergence of bacterial turbulence: phase diagram and transition kinetics. Sci. Adv. 7 (17), eabd1240.CrossRefGoogle ScholarPubMed
Qin, S. & Liao, S. 2023 A kind of Lagrangian chaotic property of the Arnold–Beltrami–Childress flow. J. Fluid Mech. 960, A15.CrossRefGoogle Scholar
Qu, A. & James, D.L. 2021 Fast linking numbers for topology verification of loopy structures. ACM Trans. Graph. 40 (4), 106:1–106:19.CrossRefGoogle Scholar
Rothman, D.H. 1989 Negative-viscosity lattice gases. J. Stat. Phys. 56 (3–4), 517–524.Google Scholar
Sanchez, T., Chen, D.T.N., DeCamp, S.J., Heymann, M. & Dogic, Z. 2012 Spontaneous motion in hierarchically assembled active matter. Nature 491 (7424), 431–434.Google Scholar
Scheeler, M.W., van Rees, W.M., Kedia, H., Kleckner, D. & Irvine, W.T.M. 2017 Complete measurement of helicity and its dynamics in vortex tubes. Science 357 (6350), 487–491.CrossRefGoogle ScholarPubMed
Słomka, J. & Dunkel, J. 2017 a Geometry-dependent viscosity reduction in sheared active fluids. Phys. Rev. Fluids 2, 043102.Google Scholar
Słomka, J. & Dunkel, J. 2017 b Spontaneous mirror-symmetry breaking induces inverse energy cascade in 3D active fluids. Proc. Natl Acad. Sci. 114 (9), 2119–2124.CrossRefGoogle ScholarPubMed
Słomka, J., Suwara, P. & Dunkel, J. 2018 The nature of triad interactions in active turbulence. J. Fluid Mech. 841, 702–731.Google Scholar
Sokolov, A., Aranson, I.S., Kessler, J.O. & Goldstein, R.E. 2007 Concentration dependence of the collective dynamics of swimming bacteria. Phys. Rev. Lett. 98 (15), 158102.CrossRefGoogle ScholarPubMed
Spitzer, F. 1958 Some theorems concerning 2-dimensional Brownian motion. Trans. Am. Math. Soc. 87 (1), 187.Google Scholar
Supekar, R., Heinonen, V., Burns, K.J. & Dunkel, J. 2020 Linearly forced fluid flow on a rotating sphere. J. Fluid Mech. 892, A30.Google Scholar
Thampi, S.P., Golestanian, R. & Yeomans, J.M. 2014 Vorticity, defects and correlations in active turbulence. Phil. Trans. R. Soc. A 372 (2029), 20130366.Google Scholar
Tribelsky, M.I. & Tsuboi, K. 1996 New scenario for transition to turbulence? Phys. Rev. Lett. 76 (10), 1631–1634.CrossRefGoogle ScholarPubMed
Urzay, J., Doostmohammadi, A. & Yeomans, J.M. 2017 Multi-scale statistics of turbulence motorized by active matter. J. Fluid Mech. 822, 762–773.Google Scholar
Vasil, G.M., Lecoanet, D., Burns, K.J., Oishi, J.S. & Brown, B.P. 2019 Tensor calculus in spherical coordinates using Jacobi polynomials. Part I. Mathematical analysis and derivations. J. Comput. Phys. 3, 100013.Google Scholar
Vologodskii, A.V. & Cozzarelli, N.R. 1994 Conformational and thermodynamic properties of supercoiled DNA. Annu. Rev. Biophys. Biomol. Struct. 23 (1), 609–643.Google Scholar
Wen, H. & Thiffeault, J.-L. 2019 Winding of a Brownian particle around a point vortex. Phil. Trans. R. Soc. A 377 (2158), 20180347.Google Scholar
Wensink, H.H., Dunkel, J., Heidenreich, S., Drescher, K., Goldstein, R.E., Löwen, H. & Yeomans, J.M. 2012 Meso-scale turbulence in living fluids. Proc. Natl Acad. Sci. 109 (36), 14308–14313.Google Scholar
Wioland, H., Woodhouse, F.G., Dunkel, J. & Goldstein, R.E. 2016 Ferromagnetic and antiferromagnetic order in bacterial vortex lattices. Nat. Phys. 12 (4), 341–345.Google Scholar
Wioland, H., Woodhouse, F.G., Dunkel, J., Kessler, J.O. & Goldstein, R.E. 2013 Confinement stabilizes a bacterial suspension into a spiral vortex. Phys. Rev. Lett. 110 (26), 268102.Google Scholar
Woltjer, L. 1958 A theorem on force-free magnetic fields. Proc. Natl Acad. Sci. 44 (6), 489–491.Google Scholar
Zuccher, S. & Ricca, R.L. 2017 Relaxation of twist helicity in the cascade process of linked quantum vortices. Phys. Rev. E 95 (5), 053109.Google Scholar