Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-17T19:28:24.326Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak shock reflection in channel flows for dense gases

Published online by Cambridge University Press:  03 July 2019

A. Kluwick  and
E. A. Cox Open the ORCID record for E. A. Cox [Opens in a new window]
A. Kluwick*
Affiliation:
Institute of Fluid Dynamics and Heat Transfer, Vienna University of Technology, Tower BA/E322, Getreidemarkt 9, 1060 Vienna, Austria
E. A. Cox
Affiliation:
School of Mathematics and Statistics, Science Centre North, University College Dublin, Belfield, Dublin 4, Ireland
*
†Email address for correspondence: alfred.kluwick@tuwien.ac.at
Get access Rights & Permissions [Opens in a new window]

Abstract

The canonical problem of transonic dense gas flows past two-dimensional compression/expansion ramps has recently been investigated by Kluwick & Cox (J. Fluid Mech., vol. 848, 2018, pp. 756–787). Their results are for unconfined flows and have to be supplemented with solutions of another canonical problem dealing with the reflection of disturbances from an opposing wall to finally provide a realistic picture of flows in confined geometries of practical importance. Shock reflection in dense gases for transonic flows is the problem addressed in this paper. Analytical results are presented in terms of similarity parameters associated with the fundamental derivative of gas dynamics 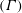$(\unicode[STIX]{x1D6E4})$, its derivative with respect to the density at constant entropy 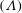$(\unicode[STIX]{x1D6EC})$ and the Mach number 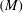$(M)$ of the upstream flow. The richer complexity of flows scenarios possible beyond classical shock reflection is demonstrated. For example: incident shocks close to normal incidence on a reflecting boundary can lead to a compound shock–wave fan reflected flow or a pure wave fan flow as well as classical flow where a compressive reflected shock attached to the reflecting boundary is observed. With incident shock angles sufficiently away from normal incidence regular reflection becomes impossible and so-called irregular reflection occurs involving a detached reflection point where an incident shock, reflected shock and a Mach stem shock which remains connected to the boundary all intersect. This triple point intersection which also includes a wave fan is known as Guderley reflection. This classical result is demonstrated to carry over to the case of dense gases. It is then finally shown that the Mach stem formed may disintegrate into a compound shock–wave fan structure generating an additional secondary upstream shock. The aim of the present study is to provide insight into flows realised, for example, in wind tunnel experiments where evidence for non-classical gas dynamic effects such as rarefaction shocks is looked for. These have been predicted theoretically by the seminal work of Thompson (Phys. Fluids, vol. 14 (9), 1971, pp. 1843–1849) but have withstood experimental detection in shock tubes so far, due to, among others, difficulties to establish purely one-dimensional flows.

JFM classification

Compressible Flows: Gas dynamics Compressible Flows: Shock waves Aerodynamics: High-speed flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 131 - 157
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alferez, N. & Touber, E. 2017 One-dimensional refraction properties of compression shocks in non-ideal gases. J. Fluid Mech. 814, 185–221.Google Scholar
Becker, R. 1922 Stosswelle und Detonation. Z. Phys. 8 (1), 321–362.Google Scholar
Bethe, H. A.1942 The theory of shock waves for an arbitrary equation of state. Technical paper 545, Office Sci. Res. & Dev.Google Scholar
Bleakney, W. & Taub, A. H. 1949 Interaction of shock waves. Rev. Mod. Phys. 21, 584–605.Google Scholar
Cachucho, A. & Skews, B. W. 2012 Guderley reflection for higher Mach numbers in a standard shock tube. Shock Waves 22 (2), 141–149.10.1007/s00193-011-0349-4Google Scholar
Cinella, P. & Congedo, P. M. 2005 Aerodynamic performance of transonic Bethe–Zel’dovich–Thompson flows past an airfoil. AIAA J. 43, 370–378.10.2514/1.8627Google Scholar
Cole, J. D. & Cook, P. 1986 Transonic Aerodynamics. Elsevier.Google Scholar
Congedo, P. M., Corre, C. & Cinella, P. 2007 Airfoil shape optimisation for transonic flows of Bethe–Zel’dovich–Thompson fluids. AIAA J. 45, 1302–1316.Google Scholar
Courant, R. & Friedrichs, K. O. 1948 Supersonic Flow and Shock Waves. Interscience Publishers.Google Scholar
Cramer, M. S. & Fry, R. N. 1993 Nozzle flows of dense gases. Phys. Fluids A 5 (5), 1246–1259.Google Scholar
Cramer, M. S. & Kluwick, A. 1984 On the propagation of waves exhibiting both positive and negative nonlinearity. J. Fluid Mech. 142, 9–37.Google Scholar
Cramer, M. S. & Tarkenton, G. M. 1992 Transonic flows of Bethe–Zel’dovich–Thompson fluids. J. Fluid Mech. 240, 197–228.10.1017/S0022112092000077Google Scholar
Dafermos, C. M. 2005 Hyperbolic Conservation Laws in Continuum Physics. Springer.Google Scholar
Duhem, P. 1909 On the propagation of shock waves in fluids. Z. Phys. Chem. 69, 169–186.Google Scholar
Earnshaw, S. 1860 On the mathematical theory of sound. Phil. Trans. R. Soc. Lond. 150, 133–148.Google Scholar
Fergason, S., Guardone, A. & Argrow, B. 2003 Construction and validation of a dense gas shock tube. J. Thermophys. Heat Transfer 17 (3), 326–333.Google Scholar
Gori, G., Vimercati, D. & Guardone, A. 2017 Non-ideal compressible-fluid effects in oblique shock waves. J. Phys. 821, 012003.Google Scholar
Guardone, A., Vigevano, L. & Argrow, B. 2004 Assessment of thermodynamic models for dense gas dynamics. Phys. Fluids 16 (11), 3878–3887.Google Scholar
Guardone, A., Zamfirescu, C. & Colonna, P. 2010 Maximum intensity of rarefaction shock waves for dense gases. J. Fluid Mech. 642, 127–146.Google Scholar
Guderley, K. G.1947 Considerations on the structure of mixed subsonic–supersonic flow patterns. Air Materiel Command Technical Report No. F-TR-2168-ND, ATI No. 22780, GS-AAF-Wright Field No. 39, U.S. Wright–Patterson Air Force Base, Dayton, OH.Google Scholar
Guderley, K. G. 1957 Theorie Schallnaher Strömungen. Springer; Translated by J. R. Moszynski, Pergamon Press, 1962.Google Scholar
Henderson, L. F. & Menikoff, R. 1998 Triple-shock entropy theorem and its consequences. J. Fluid Mech. 366, 179–210.Google Scholar
Hugoniot, H. 1887 Sur la propagation du mouvement dans les corps et spécialement dans les gaz parfaits. J. de l’Éc. Pol. Cah. LVII, 97.Google Scholar
Hugoniot, H. 1889 Mémoire sur la propagation du mouvement dans les corps et spécialement dans les gaz parfaits. Deuxième partie. J. de l’Éc. Pol. Cah. LVIII, 1–125.Google Scholar
Hunter, J. K. & Brio, M. 1997 Weak shock reflection. In Proceedings of Fifth International Congress on Sound and Vibration, Adelaide, South Australia, Dec 15–18, pp. 2023–2030. Australian Acoustical Society.Google Scholar
Hunter, J. K. & Brio, M. 2000 Weak shock reflection. J. Fluid Mech. 410, 235–261.Google Scholar
Hunter, J. K. & Tesdall, A. M. 2004 Weak shock reflection. In A Celebration of Mathematical Modeling, pp. 93–112. Springer.Google Scholar
Johnson, J. N. & Chéret, R.(Eds) 1998 Classic Papers in Shock Compression Science. Springer.Google Scholar
Kluwick, A. 1991 Small-amplitude finite-rate waves in fluids having both positive and negative nonlinearity. In Nonlinear Waves Real Fluids, pp. 1–43. Springer.Google Scholar
Kluwick, A. 1993 Transonic nozzle flow of dense gases. J. Fluid Mech. 247, 661–688.Google Scholar
Kluwick, A. 2001 Theory of shock waves. Rarefaction shocks. In Handbook of Shockwaves (ed. Ben-Dor, G., Igra, O., Elperin, T. & Lifshitz, A.), vol. 1, pp. 339–411. Academic.Google Scholar
Kluwick, A. 2017 Non-ideal compressible fluid dynamics: a challenge for theory. J. Phys. 821, 012001.Google Scholar
Kluwick, A. 2018 Shock discontinuities: from classical to non-classical shocks. Acta Mech. 229 (2), 515–533.Google Scholar
Kluwick, A. & Cox, E. A. 2018 Steady small-disturbance transonic dense gas flow past two-dimensional compression/expansion ramps. J. Fluid Mech. 848, 756–787.Google Scholar
Kluwick, A. & Kornfeld, M. 2014 Triple-deck analysis of transonic high Reynolds number flow through slender channels. Phil. Trans. R. Soc. Lond. A 372 (2020), 20130346.Google Scholar
Kluwick, A. & Meyer, G. 2010 Shock regularization in dense gases by viscous–inviscid interactions. J. Fluid Mech. 644, 473–507.Google Scholar
Kluwick, A. & Meyer, G. 2011 Viscous–inviscid interactions in transonic flows through slender nozzles. J. Fluid Mech. 672, 487–520.Google Scholar
Krehl, P. 2001 Chapter 1-History of shock waves. In Handbook of Shock Waves (ed. Ben-Dor, T. E. G., Igra, O. & Lifshitz, A.), pp. 1–142. Academic Press.Google Scholar
Lee-Bapty, I. P. & Crighton, D. G. 1987 Nonlinear wave motion governed by the modified Burgers equation. Phil. Trans. R. Soc. Lond. A 323 (1570), 173–209.Google Scholar
Mach, E.1878 Ueber den Verlauf von Funkenwellen in der Ebene und im Raume. Vienna Acad. Sitzungsberichte 78, 819.Google Scholar
Mathijssen, T.2017 Experimental observation of non-ideal compressible fluid dynamics: with application in organic rankine cycle power systems. PhD thesis, Delft University of Technology.Google Scholar
Monaco, J. F., Cramer, M. S. & Watson, L. T. 1997 Supersonic flows of dense gases in cascade configurations. J. Fluid Mech. 330, 31–59.Google Scholar
Nannan, N. R., Guardone, A. & Colonna, P. 2013 On the fundamental derivative of gas dynamics in the vapor–liquid critical region of single-component typical fluids. Fluid Phase Equilib. 337, 259–273.Google Scholar
von Neumann, J. 1963a Oblique reflection of shocks. In John von Neumann: Collected Works, 1903–1957, Vol 6 (ed. Taub, A. H.), vol. VI, pp. 238–299. Pergamon.Google Scholar
von Neumann, J. 1963b Refraction, intersection and reflection of shock waves. In John von Neumann: Collected Works, 1903–1957, Vol. 6 (ed. Taub, A. H.), vol. VI, pp. 300–308. Pergamon.Google Scholar
Oswatitsch, K. 1977 Spezialgebiete der Gasdynamik: Schallnähe, Hyperschall, Tragflächen, Wellenausbreitung. Springer.Google Scholar
Rankine, W. J. M. 1870 On the thermodynamic theory of waves of finite longitudinal disturbance. Phil. Trans. R. Soc. Lond. 160, 277–288.Google Scholar
Rusak, Z. & Wang, C.-W. 2000 Low-drag airfoils for transonic flow of dense gases. Z. Angew. Math. Phys. 51 (3), 467–480.Google Scholar
Sciacovelli, L., Cinnella, P. & Gloerfelt, X. 2017 Direct numerical simulations of supersonic turbulent channel flows of dense gases. J. Fluid Mech. 821, 153–199.Google Scholar
Serre, D. 2007 Shock reflection in gas dynamics. In Handbook of Mathematical Fluid Dynamics (ed. Friedlander, S. & Serre, D.), Handbook of Mathematical Fluid Dynamics, vol. 4, chap. 2, pp. 39–122. North-Holland.Google Scholar
Stokes, G. G. 1848 On a difficulty in the theory of sound. Philos. Mag. 33, 349–356.Google Scholar
Tabak, G. E. & Rosales, R. 1994 Focusing of weak shock waves and the von Neumann paradox of oblique shock reflection. Phys. Fluids 6, 1874–1892.Google Scholar
Tesdall, A., Sanders, R. & Popivanov, N. 2015 Further results on Guderley Mach reflection and the triple point paradox. J. Sci. Comput. 64, 721–744.Google Scholar
Tesdall, A. M. & Hunter, J. K. 2002 Self-similar solutions for weak shock reflection. SIAM J. Appl. Maths 63 (1), 42–61.Google Scholar
Thompson, P. A. 1971 A fundamental derivative in gasdynamics. Phys. Fluids 14 (9), 1843–1849.10.1063/1.1693693Google Scholar
Thompson, P. A. & Lambrakis, K. C. 1973 Negative shock waves. J. Fluid Mech. 60 (1), 187–208.Google Scholar
Vasil’ev, E. I. 1998 High-resolution simulation for the Mach reflection of weak shock waves. In Proceedings of the Fourth European Computational Fluid Dynamics Conference (ECCOMAS CFD 1998, Athens, Greece) (ed. Papailiou, K. D., Tsahalis, D., Periaux, J., Hirsch, Ch. & Pandolfi, M.), vol. 1, part 1, pp. 520–527. John Wiley & Sons.Google Scholar
Vasil’ev, E. I. & Krajko, A. N. 1999 Numerical simulation of weak shock diffraction over a wedge under the von Neumann paradox conditions. Comput. Math. Math. Phys. 39 (8), 1335–1345.Google Scholar
Vimercati, D., Kluwick, A. & Guardone, A. 2018 Oblique waves in steady supersonic flows of Bethe–Zeldovich–Thompson fluids. J. Fluid Mech. 855, 445–468.Google Scholar
Walker, J. D. A. 1998 Turbulent boundary layers II: further developments. In Recent Advances in Boundary Layer Theory (ed. Kluwick, A.), International Centre for Mechanical Sciences, vol. 390, pp. 145–230.Google Scholar
Wang, C.-W. & Rusak, Z. 1999 Numerical studies of transonic BZT gas flows around thin airfoils. J. Fluid Mech. 396, 109–141.Google Scholar
Wrabel, M. & Kluwick, A. 2005 Shock boundary layer interactions in dense gases. Proc. Annu. GAMM Meet. PAMM 4, 444–445.Google Scholar
Zeldovich, J. 1946 On the possibility of rarefaction shock waves. Zh. Eksp. Teor. Fiz. 16 (4), 363–364.Google Scholar