Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-18T20:45:50.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Models for nanoindentation of compliant films on stiff substrates

Published online by Cambridge University Press:  11 June 2015

Yang Li ,
Pavan Valavala ,
Supinda Watcharotone  and
L. Catherine Brinson
Yang Li
Affiliation:
Department of Materials Science and Engineering, Northwestern University, Evanston, Illinois 60208, USA
Pavan Valavala
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, Illinois 60208, USA
Supinda Watcharotone
Affiliation:
Department of Mechanical Engineering, Northwestern University, Evanston, Illinois 60208, USA
L. Catherine Brinson*
Affiliation:
Department of Materials Science and Engineering, Northwestern University, Evanston, Illinois 60208, USA; and Department of Mechanical Engineering, Northwestern University, Evanston, Illinois 60208, USA
*
a)Address all correspondence to this author. e-mail: cbrinson@northwestern.edu
Get access

Abstract

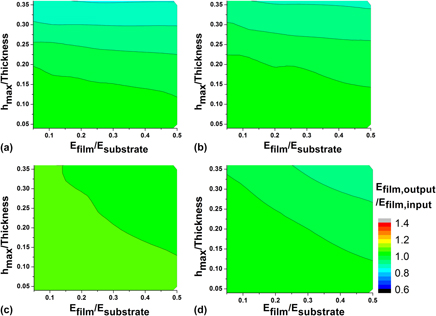
Nanoindentation is an effective approach for measuring mechanical properties of nanoscale films coated on substrates, yet results obtained through the classic Oliver–Pharr model require additional consideration due to the existence of a “substrate effect” when the film is much more compliant than the substrate. In this study, different models for removing this substrate effect are compared, with focus on the Gao model, the Saha–Nix model, and the Hay model and the use of a direct finite element (FE) approach is discussed. Validity of these models is examined using load–displacement data obtained from simulated indentation of an elastic–plastic film in FEs. It is found that the performance of the analytical models varies significantly with different testing parameters, including ratio between film modulus and substrate modulus (Ef/Es), indenting ratio (hmax/film thickness), and yield strain. Choices of using a nanoindentation model to process experimental data should be made according to estimated indentation depth and modulus difference between film and substrate. An example of applying substrate removal models to experimental data is also shown.

Keywords

nanoindentationfilmsimulation
Type
Articles
Information
Journal of Materials Research , Volume 30 , Issue 11 , 14 June 2015 , pp. 1747 - 1760
Copyright
Copyright © Materials Research Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Susan B. Sinnott

References

REFERENCES

Hertz, H.: On the contact of elastic solids. J Reine Angew Math. 92, 16 (1881).Google Scholar
Hertz, H.: On hardness. Verh. Ver. Bedorderung Gewerbe Fleisses. 61, (1882).Google Scholar
Sneddon, I.N.: The relation between load and penetration in the axisymmetric boussinesq problem for a punch of arbitrary profile. Int. J. Eng. Sci. 3(1), 11 (1965).CrossRefGoogle Scholar
King, R.B.: Elastic analysis of some punch problems for a layered medium. Int. J. Solids Struct. 23(12), 8 (1987).CrossRefGoogle Scholar
Pharr, G.M., Oliver, W.C., and Brotzen, F.R.: On the generality of the relationship among contact stiffness, contact area, and elastic-modulus during indentation. J. Mater. Res. 7(3), 613 (1992).CrossRefGoogle Scholar
Doerner, M.F. and Nix, W.D.: A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 1(4), 9 (1986).CrossRefGoogle Scholar
Hay, J. and Crawford, B.: Measuring substrate-independent modulus of thin films. J. Mater. Res. 26(6), 727 (2011).CrossRefGoogle Scholar
Saha, R. and Nix, W.D.: Effects of the substrate on the determination of thin film mechanical properties by nanoindentation. Acta Mater. 50, 16 (2002).CrossRefGoogle Scholar
Watcharotone, S., Wood, C.D., Friedrich, R., Chen, X.Q., Qiao, R., Putz, K., and Brinson, L.C.: Interfacial and substrate effects on local elastic properties of polymers using coupled experiments and modeling of nanoindentation. Adv. Eng. Mater. 13(5), 400 (2011).CrossRefGoogle Scholar
Wei, Z., Zhang, G., Chen, H., Luo, J., Liu, R., and Guo, S.: A simple method for evaluating elastic modulus of thin films by nanoindentation. J. Mater. Res. 24(3), 801 (2009).CrossRefGoogle Scholar
Gao, H., Chiu, C., and Lee, J.: Elastic contact versus indentation modeling of multi-layered materials. Int. J. Solids Struct. 29(20), 22 (1992).Google Scholar
Mencik, J., Munz, D., Quandt, E., Weppelmann, E.R., and Swain, M.V.: Determination of elastic modulus of thin layers using nanoindentation. J. Mater. Res. 12(9), 10 (1997).CrossRefGoogle Scholar
Li, H. and Vlassak, J.J.: Determining the elastic modulus and hardness of an ultra-thin film on a substrate using nanoindentation. J. Mater. Res. 24(3), 1114 (2009).CrossRefGoogle Scholar
Zhou, B. and Prorok, B.C.: A new paradigm in thin film indentation. J. Mater. Res. 25(9), 1671 (2010).CrossRefGoogle Scholar
Miyake, K., Satomi, N., and Sasaki, S.: Elastic modulus of polystyrene film from near surface to bulk measured by nanoindentation using atomic force microscopy. Appl. Phys. Lett. 89(3), (2006).CrossRefGoogle Scholar
Chen, W.T.: Computation of stresses and displacements in a layered elastic medium. Int. J. Eng. Sci. 9, 25 (1971).CrossRefGoogle Scholar
Chen, W.T. and Engel, P.A.: Impact and contact stress analysis in Multilayer Media. Int. J. Solids Struct. 8, 25 (1972).CrossRefGoogle Scholar
Yu, H.Y., Sanday, S.C., and Rath, B.B.: The effect of substrate on the elastic properties of films determined by the indentation test—axisymmetrical boussinesq problem. J. Mech. Phys. Solids 38(6), 745 (1990).CrossRefGoogle Scholar
Zhao, M., Chen, X., Xiang, Y., Vlassak, J.J., Lee, D., Ogasawara, N., Chiba, N., and Gan, Y.X.: Measuring elastoplastic properties of thin films on an elastic substrate using sharp indentation. Acta Mater. 55(18), 6260 (2007).CrossRefGoogle Scholar
Da Silva Botelho, T., Progri, R., Inglebert, G., and Robbe-Valloire, F.: Analytical and experimental elastoplastic spherical indentations of a layered half-space. Mech. Mater. 40(10), 771 (2008).CrossRefGoogle Scholar
Chen, W.W., Zhou, K., Keer, L.M., and Wang, Q.J.: Modeling elasto-plastic indentation on layered materials using the equivalent inclusion method. Int. J. Solids Struct. 47(20), 2841 (2010).CrossRefGoogle Scholar
Polonsky, I.A. and Keer, L.M.: A fast and accurate method for numerical analysis of elastic layered contacts. J. Tribol. 122, 6 (2000).CrossRefGoogle Scholar
Liu, S., Wang, Q., and Liu, G.: A versatile method of discrete convolution and FFT (DC-FFT) for contact analyses. Wear 243(1–2), 11 (2000).CrossRefGoogle Scholar
Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7(6), 20 (1992).CrossRefGoogle Scholar
Oliver, W.C. and Pharr, G.M.: Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 19(1), 18 (2004).CrossRefGoogle Scholar
Pharr, G.M., Strader, J.H., and Oliver, W.C.: Critical issues in making small-depth mechanical property measurements by nanoindentation with continuous stiffness measurement. J. Mater. Res. 24(3), 653 (2009).CrossRefGoogle Scholar
Hay, J.C., Bolshakov, A., and Pharr, G.M.: A critical examination of the fundamental relations used in the analysis of nanoindentation data. J. Mater. Res. 14(6), 2296 (1999).CrossRefGoogle Scholar
Pharr, G.M. and Oliver, W.C.: Measurement of thin-film mechanical-properties using nanoindentation. MRS Bull. 17(7), 28 (1992).CrossRefGoogle Scholar
Chen, K.S., Chen, T.C., and Ou, K.S.: Development of semi-empirical formulation for extracting materials properties from nanoindentation measurements: Residual stresses, substrate effect, and creep. Thin Solid Films 516(8), 1931 (2008).CrossRefGoogle Scholar
Bolshakov, A. and Pharr, G.M.: Influences of pileup on the measurement of mechanical properties by load and depth sensing indentation techniques. J. Mater. Res. 13(4), 10 (1998).CrossRefGoogle Scholar
Stone, D.S., Yoder, K.B., and Sproul, W.D.: Hardness and elastic modulus of TiN based on continuous indentation technique and new correlation. J. Vac. Sci. Technol., A 9(4), 5 (1991).CrossRefGoogle Scholar
Neuber, H.: Kerbspannungslehve (Springer Berlin, Berlin, 1946).Google Scholar
Xu, H. and Pharr, G.: An improved relation for the effective elastic compliance of a film/substrate system during indentation by a flat cylindrical punch. Scr. Mater. 55(4), 315 (2006).CrossRefGoogle Scholar
Song, H.: Selected Mechanical Problems in Load- and Depth-sensing Indentation Testing (Rice University, 1999).Google Scholar
Cheng, Y.T. and Cheng, C.M.: Scaling relationships in conical indentation of elastic perfectly plastic solids. Int. J. Solids Struct. 36(8), 1231 (1999).CrossRefGoogle Scholar
Knapp, J.A., Follstaedt, D.M., Myers, S.M., Barbour, J.C., and Friedmann, T.A.: Finite-element modeling of nanoindentation. J. Appl. Phys. 85(3), 1460 (1999).CrossRefGoogle Scholar
Chen, X. and Vlassak, J.J.: Numerical study on the measurement of thin film mechanical properties by means of nanoindentation. J. Mater. Res. 16(10), 2974 (2001).CrossRefGoogle Scholar
Zeng, K.Y. and Shen, L.: A new analysis of nanoindentation load–displacement curves. Philos. Mag. A 82(10), 2223 (2002).CrossRefGoogle Scholar
Xu, Z.H. and Rowcliffe, D.: Finite element analysis of substrate effects on indentation behaviour of thin films. Thin Solid Films 447, 399 (2004).CrossRefGoogle Scholar
Chollacoop, N., Li, L., and Gouldstone, A.: Errors in resolved modulus during nano-indentation of hard films on soft substrates: A computational study. Mater. Sci. Eng., A 423(1–2), 36 (2006).CrossRefGoogle Scholar
Tsui, T.Y., Vlassak, J., and Nix, W.D.: Indentation plastic displacement field: Part I. The case of soft films on hard substrates. J. Mater. Res. 14(6), 2196 (1999).CrossRefGoogle Scholar
Hamming, L.M., Qiao, R., Messersmith, P.B., and Brinson, L.C.: Effects of dispersion and interfacial modification on the macroscale properties of TiO(2) polymer-matrix nanocomposites. Compos Sci Technol. 69(11–12), 1880 (2009).CrossRefGoogle ScholarPubMed
Qiao, R., Deng, H., Putz, K.W., and Brinson, L.C.: Effect of particle agglomeration and interphase on the glass transition temperature of polymer nanocomposites. J. Polym. Sci., Part B: Polym. Phys. 49(10), 740 (2011).CrossRefGoogle Scholar
Deng, H., Liu, Y., Gai, D.H., Dikin, D.A., Putz, K.W., Chen, W., Brinson, L.C., Burkhart, C., Poldneff, M., Jiang, B., and Papakonstantopoulos, G.J.: Utilizing real and statistically reconstructed microstructures for the viscoelastic modeling of polymer nanocomposites. Compos. Sci. Technol. 72(14), 1725 (2012).CrossRefGoogle Scholar
Torkelson, J.M. and Ellison, C.J.: The distribution of glass-transition temperatures in nanoscopically confined glass formers. Nat. Mater. 2(10), 695 (2003).Google Scholar
Rittigstein, P., Priestley, R.D., Broadbelt, L.J., and Torkelson, J.M.: Model polymer nanocomposites provide an understanding of confinement effects in real nanocomposites. Nat. Mater. 6(4), 278 (2007).CrossRefGoogle ScholarPubMed
Supplementary material: File

Li et al.

Supplementary Material

Download Li et al.(File)
File 227.6 KB