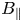1. Introduction
A long-standing goal of tokamak simulation has been to create a full-device model capable of treating large-scale motion such as global magnetohydrodynamic (MHD) modes in conjunction with gyroscale turbulence. Even simulating individual global MHD-related modes with full kinetic effects often requires correct treatment of plasma motion at the gyroscale: fine-scale layers occur as a result of coupling to continua and nearly singular behaviour near rational surfaces.
I refer to any gyrokinetic theory that orders the perpendicular fluctuation length scales to be small compared with the system length as scale-separated gyrokinetics; this is fundamental to local gyrokinetics, but also near-universal in applied global gyrokinetics, which mostly follows treatments of Hahm (Reference Hahm1988) or Frieman & Chen (Reference Frieman and Chen1982). This ordering is not compatible with the treatment of system-scale MHD-ordered dynamics. These shortcomings came to light first in the context of the system-scale Poisson equation (motivating multiscale approaches to correctly evolve the slow dynamics at the system scale (Abel et al. Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013)): here, I consider issues that arise in an electromagnetic context, which is less well explored (Martin-Collar et al. Reference Martin-Collar, McMillan, Saarelma and Bottino2020). Scale separation is key to the derivation of Hahm (Reference Hahm1988), and allows certain simplifications to be made because perpendicular spatial derivatives of the fluctuations can be assumed larger than those involving the background field; corrections then arise at higher order (Parra & Calvo Reference Parra and Calvo2011; Dudkovskaia Reference Dudkovskaia, Wilson, Connor, Dickinson and Parra2023). One place that this separation-of-scales simplification is used is to decouple the field equations into parallel and perpendicular components involving $A_{\|}$![]() and $B_{\|}$
and $B_{\|}$![]() respectively, which is only possible in the short-wavelength limit (moreover, the resulting field is not necessarily even divergence-free). A more subtle way a simplification arises is when the the near-identity guiding-centre transform is neglected when a perturbation is introduced (Hahm Reference Hahm1988). Despite this, it is relatively common for global scale-separated gyrokinetic codes to resolve and discuss the system-scale dynamics in their simulations. Our goal here is not to discuss whether this is useful; arguments that global gyrokinetics might be effective even for formally excluded phenomena (Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2019) have been made, but this is strenuously disputed (Parra & Catto Reference Parra and Catto2009).
respectively, which is only possible in the short-wavelength limit (moreover, the resulting field is not necessarily even divergence-free). A more subtle way a simplification arises is when the the near-identity guiding-centre transform is neglected when a perturbation is introduced (Hahm Reference Hahm1988). Despite this, it is relatively common for global scale-separated gyrokinetic codes to resolve and discuss the system-scale dynamics in their simulations. Our goal here is not to discuss whether this is useful; arguments that global gyrokinetics might be effective even for formally excluded phenomena (Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2019) have been made, but this is strenuously disputed (Parra & Catto Reference Parra and Catto2009).
Instead, I will discuss what would be needed to produce a minimal consistent gyrokinetic model for global plasma dynamics (that allows MHD-like motion) and explore how one might practically implement a consistent treatment. This appears to require not an extension of typical gyrokinetic time-evolution schemes but something much closer to an extended kinetic MHD scheme; this is conceptually similar to the gyrokinetic electromagnetic treatment explored by Morrison (Reference Morrison2013), but uses the Darwin (low-frequency) limit of Maxwell's equations. Explaining why this scheme is needed and how it would work is one major aim of this paper. The other is to make some simple practical progress to implement this formalism, to demonstrate that this kind of approach has potential for application, so it can serve as more than just a framework for theoretical discussion.
One important requirement for useful simulation of large-scale tokamak dynamics is reproduction of MHD in the appropriate limits, in addition to gyroscale drift modes. The simplest kinetic theory that is able to capture global MHD-ordered dynamics is drift kinetics. Various fluid models may be directly derived from drift kinetics, including various forms of full (Grad Reference Grad1966; Kulsrud Reference Kulsrud1983; Takahashi, Brennan & Kim Reference Takahashi, Brennan and Kim2009) and reduced (Miyato et al. Reference Miyato, Scott, Strintzi and Tokuda2009) MHD. Early papers on guiding-centre models (Sagdeyev et al. Reference Sagdeyev, Kadomtsev, Rudakov and Vedyonov1958; Grad Reference Grad1966) describe how the drift-kinetic models (i.e equations for the guiding centres) may be transformed into fluid equations. Drift-kinetic models may also be recast in the form of kinetic MHD models (Kulsrud Reference Kulsrud1983) (as well as guiding-centre MHD models, gyrokinetic MHD models exist (Burby & Tronci Reference Burby and Tronci2017)), where the kinetic equations provide closure to the fluid equations, through modified current and/or pressure terms. In a maximalist treatment of kinetic MHD that treats every species kinetically, the kinetic equations are used to provide closure to the fluid equations, so the kinetic physics is fully equivalent to direct kinetic modelling. The Lorentz force in kinetic MHD is also fully equivalent to a direct drift-kinetic treatment, because the currents match. One place where kinetic MHD models almost invariably use a simplified treatment is in Ohm's law, which is usually assumed to be the ideal MHD Ohm's law, possible with bulk resistivity (Takahashi et al. Reference Takahashi, Brennan and Kim2009); this rules out the treatment of various kinds of sound- and drift-related dynamics where the kinetic origin of the electric field is crucial. Capturing the kinetic physics that gives rise to a finite parallel electric field can be improved by more detailed modelling of electrons (Lyster & Leboeuf Reference Lyster and Leboeuf1992). Practical applications/implementations of kinetic MHD models do not usually follow a maximalist approach, because their reason for existence is to allow a simplified, and thus numerically more tractable, treatment of the background plasma; such codes often consist of a MHD code coupled to a kinetic solver for high-energy particles.
Certain aspects of the relationship between gyrokinetics and drift kinetics have been explored earlier; Duthoit, Hahm & Wang (Reference Duthoit, Hahm and Wang2014) was able to find long-wavelength field and kinetic equations that matched drift-kinetic formulae at intermediate scales where both the theories presented were valid. Gyrokinetics may be written in the form of a small correction to drift-kinetic theory (Dimits Reference Dimits2010; McMillan & Sharma Reference McMillan and Sharma2016), which provides a pathway to implementations that are able to correctly treat both gyroscale and system-scale motion, by modifying a drift-kinetic solution scheme. As a preliminary step to implementing such a framework, I investigate what differences exist between typical global gyrokinetic models and a general MHD-compatible drift-kinetic model. I proceed with this by considering these theories in a variational framework, where the compact representation of the theories simplifies the comparison, and one can unambiguously identify certain currents and conservation relations (Burby & Tronci Reference Burby and Tronci2017). Some re-derivations of drift-kinetic field equations are presented here, in order to illustrate where standard gyrokinetic theory is incompatible with global MHD. This mostly occurs because gyrokinetic derivations drop system-scale derivatives compared to perpendicular fluctuation derivatives. One necessary requirement for modelling system-scale MHD-like dynamics is for the model to be able to represent the system-scale equilibrium correctly, and, in particular, equilibrium currents. This is the case even for codes that are only designed to study fluctuations, because the model needs to faithfully represent nearby equilibria that differ from the assumed background state. Equilibrium currents are crucial, in particular, in the drive mechanism of kink and tearing modes.
Because at the system scale fluctuations parallel and perpendicular to the magnetic field do not decouple (in the sense, for example, that currents parallel to the field can produce magnetic field fluctuations with a parallel component), formulations that solve field equations in terms of the full $\boldsymbol {E}$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() vectors are useful, and in general one must allow the fields to evolve as dynamical quantities. Recently, approaches which are not only gauge-invariant, but where only the electromagnetic fields (and not potentials) appear in the field equations and equations of motion have been proposed as a useful and practical approach to gyrokinetics (Duthoit et al. Reference Duthoit, Hahm and Wang2014; Burby & Brizard Reference Burby and Brizard2019; Zonta et al. Reference Zonta, Iorio, Burby, Liu and Hirvijoki2021). The use of physical fields rather than gauge-dependent quantities is desirable, but it is a somewhat radical difference from typical gyrokinetic approaches. Keeping time-evolving fields in the symplectic form is another departure from certain forms of gyrokinetics where the perturbed fields appear only as an effective potential. A time-evolving symplectic form leads to the appearance of time derivatives of fields in the particle equations of motion, which is presented as an obstacle to numerical implementation of kinetic theory in various previous works, but is actually standard in basic (i.e. non-gyrokinetic) treatment of particle motion in electromagnetic fields, and has a relatively simple interpretation in light of MHD motion. One can thus recover field equations in the form of kinetically modified MHD. That is, an Ohm's law and a perpendicular momentum equation, with relevant drift-kinetic effects captured.
vectors are useful, and in general one must allow the fields to evolve as dynamical quantities. Recently, approaches which are not only gauge-invariant, but where only the electromagnetic fields (and not potentials) appear in the field equations and equations of motion have been proposed as a useful and practical approach to gyrokinetics (Duthoit et al. Reference Duthoit, Hahm and Wang2014; Burby & Brizard Reference Burby and Brizard2019; Zonta et al. Reference Zonta, Iorio, Burby, Liu and Hirvijoki2021). The use of physical fields rather than gauge-dependent quantities is desirable, but it is a somewhat radical difference from typical gyrokinetic approaches. Keeping time-evolving fields in the symplectic form is another departure from certain forms of gyrokinetics where the perturbed fields appear only as an effective potential. A time-evolving symplectic form leads to the appearance of time derivatives of fields in the particle equations of motion, which is presented as an obstacle to numerical implementation of kinetic theory in various previous works, but is actually standard in basic (i.e. non-gyrokinetic) treatment of particle motion in electromagnetic fields, and has a relatively simple interpretation in light of MHD motion. One can thus recover field equations in the form of kinetically modified MHD. That is, an Ohm's law and a perpendicular momentum equation, with relevant drift-kinetic effects captured.
In the first part of the paper, I review and compare variational forms for minimal drift-kinetic and gyrokinetic models of interest. I then discuss issues of equilibrium distribution functions in these theories and describe a (new) relatively simple analytical background distribution that is both consistent with MHD currents and a solution to the Vlasov equations to the order required: parallel equilibrium currents are crucial to modelling, for example, kink modes (Dudkovskaia Reference Dudkovskaia, Wilson, Connor, Dickinson and Parra2023), so this is a basic condition for modelling them correctly. This analysis allows us to show that there are components of global currents missing from typical global formulations of gyrokinetics. I then review practical implementational issues for a system-scale drift-kinetic formulation, providing a (novel) set of field equations that resemble kinetic MHD, with an extended momentum law and Ohm's law. I then use a periodic two-dimensional (2-D) MHD equilibrium to provide a proof-of-principle implementation of the guiding-centre Maxwell equations, solving for the dynamics of the electric and magnetic fields. This testcase is intended as a springboard for numerical investigations of the properties of more complex gyrokinetic formulations. This scheme is consistent with an extended version of kinetic MHD, as might be expected. This framework is not perturbative, i.e. there is no splitting into background and fluctuations, and this both simplifies the presentation in certain ways, and also makes it appropriate for modelling large-amplitude dynamics.
2. Variational theories for drift kinetics and gyrokinetics
In this section I review the relationship between drift-kinetic theory and gyrokinetic theory; this allows us to explain what additional physics must be retained in a gyrokinetic code in order for it to capture correctly system-scale MHD-ordered motion. Strong-flow drift-kinetic Lagrangians are presented here, consistent with MHD: this promotes the dynamics of plasma motion to low order in the theory compared with standard weak-flow gyrokinetic theory, and thus bypasses some of the complexities that appear at higher order. The weak-flow gyrokinetic formalism implemented in ORB5 (Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2019) is used as a baseline; many of the global codes make similar geometrical approximations, so most of the considerations generalise.
In drift-kinetic and gyrokinetic theory, the overall Lagrangian may be decomposed into an expression for the field Lagrangian, which is the same for both theories (and just magnetic energy density where quasi-neutrality is assumed), and a per-particle Lagrangian $L_p$![]() , with a system Lagrangian $L_s = \int _Z L_p + \int _R L_f$
, with a system Lagrangian $L_s = \int _Z L_p + \int _R L_f$![]() (the integrals are over particle phase space and volume respectively). Largely, I will be working within a drift-kinetic ordering, where, given system length scale $R$
(the integrals are over particle phase space and volume respectively). Largely, I will be working within a drift-kinetic ordering, where, given system length scale $R$![]() , the small parameter is $\rho ^* \equiv \rho /R \ll 1$
, the small parameter is $\rho ^* \equiv \rho /R \ll 1$![]() , with $\rho$
, with $\rho$![]() the thermal gyroradius, flows are sonic, with the thermal speed $v_t \sim E/B$
the thermal gyroradius, flows are sonic, with the thermal speed $v_t \sim E/B$![]() , so fields are ordered $q \phi \sim q A v_t \sim m v_t^2/\rho ^*$
, so fields are ordered $q \phi \sim q A v_t \sim m v_t^2/\rho ^*$![]() , except parallel fields are smaller, with $R E_{\|} \sim m v^2$
, except parallel fields are smaller, with $R E_{\|} \sim m v^2$![]() , and time scales $\tau \sim R/v_t$
, and time scales $\tau \sim R/v_t$![]() so that $\tau q B/m \gg 1$
so that $\tau q B/m \gg 1$![]() . The drift-kinetic particle Lagrangian may be written (Littlejohn Reference Littlejohn1983) up to first order in $\rho ^*$
. The drift-kinetic particle Lagrangian may be written (Littlejohn Reference Littlejohn1983) up to first order in $\rho ^*$![]() (keeping strong flow terms) as
(keeping strong flow terms) as
Here, the particle phase space is labelled as $(\boldsymbol {R}, v_{\|}, \mu )$![]() , with the (to lowest order) correspondence to standard laboratory-frame coordinates in that $\mu B$
, with the (to lowest order) correspondence to standard laboratory-frame coordinates in that $\mu B$![]() is the perpendicular particle kinetic energy, $v_{\|}$
is the perpendicular particle kinetic energy, $v_{\|}$![]() the parallel velocity, $\boldsymbol {R}$
the parallel velocity, $\boldsymbol {R}$![]() the guiding-centre position and ${\rm d}\theta /{\rm d}t$
the guiding-centre position and ${\rm d}\theta /{\rm d}t$![]() the rate of change of gyroangle. Here $\boldsymbol {B}$
the rate of change of gyroangle. Here $\boldsymbol {B}$![]() is the magnetic field vector, $\boldsymbol {A}$
is the magnetic field vector, $\boldsymbol {A}$![]() (with $\boldsymbol {\nabla } \times \boldsymbol {A} = \boldsymbol {B}$
(with $\boldsymbol {\nabla } \times \boldsymbol {A} = \boldsymbol {B}$![]() ) is the vector potential, $\boldsymbol {E}$
) is the vector potential, $\boldsymbol {E}$![]() is the electric field, $\phi$
is the electric field, $\phi$![]() is the electrostatic field (with $\boldsymbol {E} = -\boldsymbol {\nabla } \phi - \partial \boldsymbol {A}/ \partial t$
is the electrostatic field (with $\boldsymbol {E} = -\boldsymbol {\nabla } \phi - \partial \boldsymbol {A}/ \partial t$![]() ) and $\boldsymbol {b}=\boldsymbol {B}/B$
) and $\boldsymbol {b}=\boldsymbol {B}/B$![]() , and these are evaluated at the guiding-centre position. Parameters $m$
, and these are evaluated at the guiding-centre position. Parameters $m$![]() and $q$
and $q$![]() are the particle mass and charge respectively, and perpendicular components are taken using $\boldsymbol {G}_{\perp } = \boldsymbol {G} - \boldsymbol {b} \boldsymbol {b} \boldsymbol {\cdot } \boldsymbol {G}$
are the particle mass and charge respectively, and perpendicular components are taken using $\boldsymbol {G}_{\perp } = \boldsymbol {G} - \boldsymbol {b} \boldsymbol {b} \boldsymbol {\cdot } \boldsymbol {G}$![]() . Note the appearance of the coupling between the potentials $(\boldsymbol {A},\phi )$
. Note the appearance of the coupling between the potentials $(\boldsymbol {A},\phi )$![]() and the trajectory $({\rm d}\boldsymbol {R},{\rm d}t)$
and the trajectory $({\rm d}\boldsymbol {R},{\rm d}t)$![]() in a four-vector (contravariant) form, which is sufficient to ensure the equations of motion and field equations may be written in terms of the physical fields $\boldsymbol {E}$
in a four-vector (contravariant) form, which is sufficient to ensure the equations of motion and field equations may be written in terms of the physical fields $\boldsymbol {E}$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() (rather than electromagnetic gauge-dependent $\boldsymbol {A}$
(rather than electromagnetic gauge-dependent $\boldsymbol {A}$![]() and $\phi$
and $\phi$![]() ).
).
This particle Lagrangian is equivalent, to this order, to the expression
obtained using a different choice of parallel velocity coordinate (Parra & Calvo Reference Parra and Calvo2011; Burby, Squire & Qin Reference Burby, Squire and Qin2013) (discussions on the Baños drift explain why this difference arises (Northrop & Rome Reference Northrop and Rome1978)). These first-order expressions are sufficient to find the Euler–Lagrange equations for $\boldsymbol {\dot {R}}$![]() and $\dot {v}_{\|}$
and $\dot {v}_{\|}$![]() at the same order (Burby & Tronci Reference Burby and Tronci2017). This gives the currents in the plasma up to the order of the diamagnetic drifts, sufficient to resolve MHD-ordered currents and plasma motion. Indeed two-fluid and MHD theory may be derived directly from these equations, on taking moments and enforcing the highly collisional limit.
at the same order (Burby & Tronci Reference Burby and Tronci2017). This gives the currents in the plasma up to the order of the diamagnetic drifts, sufficient to resolve MHD-ordered currents and plasma motion. Indeed two-fluid and MHD theory may be derived directly from these equations, on taking moments and enforcing the highly collisional limit.
For the purposes of, for example, linear stability theory for plasmas with weak flows (or local gyrokinetics), the polarisation term may be simplified to a Boussinesq-type form by considering it to be integrated with respect to a fixed background distribution function and magnetic field, yielding a term $({m n_0}/{2 B_0^2}) E_{\perp 0}^2$![]() after velocity-space integration, where the perpendicular projector is relative to the assumed background field. This gives rise to a linearised polarisation term, which appears as a field term, rather than in the particle Hamiltonian; as a result, the particles are not subject to the ponderomotive drift.
after velocity-space integration, where the perpendicular projector is relative to the assumed background field. This gives rise to a linearised polarisation term, which appears as a field term, rather than in the particle Hamiltonian; as a result, the particles are not subject to the ponderomotive drift.
To simplify (2.2) to a representative Lagrangian associated with a global gyrokinetic code, the replacement $\boldsymbol {A} = \boldsymbol {A}_0 + \boldsymbol {b} A_{\|} + \boldsymbol {A}_\perp$![]() is made, with $A_{\|},\boldsymbol {A}_{\perp }$
is made, with $A_{\|},\boldsymbol {A}_{\perp }$![]() taken one order smaller (the parameter is $\epsilon _E \sim A_{\|}/A \sim E/B_0 v_t$
taken one order smaller (the parameter is $\epsilon _E \sim A_{\|}/A \sim E/B_0 v_t$![]() so this is also a small flow ordering) than $\boldsymbol {A}$
so this is also a small flow ordering) than $\boldsymbol {A}$![]() . For modes with short perpendicular wavelength, $A_{\|}$
. For modes with short perpendicular wavelength, $A_{\|}$![]() gives rise to magnetic field fluctuations that are mostly perpendicular to the background field, and the $A_{\perp }$
gives rise to magnetic field fluctuations that are mostly perpendicular to the background field, and the $A_{\perp }$![]() term gives rise to a field strength fluctuation $\boldsymbol {\nabla } \times \boldsymbol {A}_{\perp } \sim \boldsymbol {b} B_{\|}$
term gives rise to a field strength fluctuation $\boldsymbol {\nabla } \times \boldsymbol {A}_{\perp } \sim \boldsymbol {b} B_{\|}$![]() . With these simplifications
. With these simplifications

where fluctuations in $\boldsymbol {b}$![]() and in $B$
and in $B$![]() (except in the energy $\mu B$
(except in the energy $\mu B$![]() ) result in second-order mixed terms not explicitly evaluated (Parra & Calvo Reference Parra and Calvo2011). Here $\boldsymbol {A}_{\perp }$
) result in second-order mixed terms not explicitly evaluated (Parra & Calvo Reference Parra and Calvo2011). Here $\boldsymbol {A}_{\perp }$![]() is removed from the symplectic term through a small coordinate shift, the approximation $\boldsymbol {b} B_{\|} \sim \boldsymbol {\nabla } \times \boldsymbol {A}_{\perp }$
is removed from the symplectic term through a small coordinate shift, the approximation $\boldsymbol {b} B_{\|} \sim \boldsymbol {\nabla } \times \boldsymbol {A}_{\perp }$![]() is used and the orderings on time and spatial variations allow one to use an electrostatic polarisation term, thus neglecting the kinetic energy associated with fast waves. Equation (2.3) may be compared with, for example, the Lagrangian (expressed in $v_{\|}$
is used and the orderings on time and spatial variations allow one to use an electrostatic polarisation term, thus neglecting the kinetic energy associated with fast waves. Equation (2.3) may be compared with, for example, the Lagrangian (expressed in $v_{\|}$![]() form (Mishchenko et al. Reference Mishchenko, Könies, Kleiber and Cole2014)) used in ORB5 gyrokinetic code (Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2019). At this point, the remaining differences between ORB5 gyrokinetic theory and this drift-kinetic Lagrangian are through the gyroaverages on the perturbed fields $A_{\|}$
form (Mishchenko et al. Reference Mishchenko, Könies, Kleiber and Cole2014)) used in ORB5 gyrokinetic code (Lanti et al. Reference Lanti, Ohana, Tronko, Hayward-Schneider, Bottino, McMillan, Mishchenko, Scheinberg, Biancalani and Angelino2019). At this point, the remaining differences between ORB5 gyrokinetic theory and this drift-kinetic Lagrangian are through the gyroaverages on the perturbed fields $A_{\|}$![]() and $\phi$
and $\phi$![]() and the neglect of $B_{\|}$
and the neglect of $B_{\|}$![]() (various other global codes include $B_{\|}$
(various other global codes include $B_{\|}$![]() (Dannert & Jenko Reference Dannert and Jenko2005)). Also, some of these terms are integrated with the background distribution $f_0$
(Dannert & Jenko Reference Dannert and Jenko2005)). Also, some of these terms are integrated with the background distribution $f_0$![]() and not the full $f$
and not the full $f$![]() . In the long-wavelength ordering gyroaveraging leads to a modification to the perturbed particle motion two orders in $\rho ^*$
. In the long-wavelength ordering gyroaveraging leads to a modification to the perturbed particle motion two orders in $\rho ^*$![]() lower than that due to the perturbed motion itself, and to a modification to the current at least one order lower than the perturbed currents (some currents nearly cancel).
lower than that due to the perturbed motion itself, and to a modification to the current at least one order lower than the perturbed currents (some currents nearly cancel).
The field $\boldsymbol {b} B_{\|}$![]() is not divergence-free in general, which would require $\boldsymbol {b} \boldsymbol {\cdot } \boldsymbol {\nabla } (B_{\|}/B_0) = 0$
is not divergence-free in general, which would require $\boldsymbol {b} \boldsymbol {\cdot } \boldsymbol {\nabla } (B_{\|}/B_0) = 0$![]() , and the divergence of the field is only ‘small’ if the fluctuation has short perpendicular wavelength. Whether this matters practically is unclear, although any derivation that assumes magnetic fields are divergence-free will not hold. This Lagrangian also no longer possesses explicit electromagnetic gauge invariance. Additionally, as a consequence of the different treatment of background and perturbed fields, it no longer has the Hamiltonian structure of Morrison (Reference Morrison2013).
, and the divergence of the field is only ‘small’ if the fluctuation has short perpendicular wavelength. Whether this matters practically is unclear, although any derivation that assumes magnetic fields are divergence-free will not hold. This Lagrangian also no longer possesses explicit electromagnetic gauge invariance. Additionally, as a consequence of the different treatment of background and perturbed fields, it no longer has the Hamiltonian structure of Morrison (Reference Morrison2013).
In the quasi-neutral limit, electric field energy is ignored and the drift-kinetic field Lagrangian is given as
whereas the standard electromagnetic gyrokinetic formalism has
which is equivalent for fields $\boldsymbol {A} = \boldsymbol {A}_0 + \boldsymbol {b} A_{\|}$![]() with short perpendicular wavelength as
with short perpendicular wavelength as
where the variation of $\boldsymbol {b}$![]() has been ignored.
has been ignored.
Although one could attempt to repair the field representation and retain additional terms in the gyrokinetic Lagrangian to ensure it matches the drift-kinetic Lagrangian in the long-wavelength limit, a more direct approach is to retain the full magnetic field perturbation in the symplectic form, given that, for example, the parallel and perpendicular field equations will in either case be coupled. In this direct approach, the field equations, which are presented explicitly in § 5, contain an implicit dependence on $\partial \boldsymbol {E} / \partial t$![]() . Slightly more complicated Euler–Lagrange equations also arise, especially compared with a Hamiltonian formulation where $A_{\|}$
. Slightly more complicated Euler–Lagrange equations also arise, especially compared with a Hamiltonian formulation where $A_{\|}$![]() appears only in a modified potential. Many of the quantities solved have exactly the same interpretation in drift-kinetic and gyrokinetic theory, such as the electromagnetic fields $A_{\|}$
appears only in a modified potential. Many of the quantities solved have exactly the same interpretation in drift-kinetic and gyrokinetic theory, such as the electromagnetic fields $A_{\|}$![]() and $\phi$
and $\phi$![]() .
.
The particle equations of motion resulting from these Lagrangians (Cary & Brizard Reference Cary and Brizard2009) may be expressed as

with $\boldsymbol {B}^* = \boldsymbol {\nabla } \times \boldsymbol {A}^*$![]() , $\boldsymbol {A}^*$
, $\boldsymbol {A}^*$![]() the term multiplying $\textrm {d}\boldsymbol {R}$
the term multiplying $\textrm {d}\boldsymbol {R}$![]() in the one-form, and $q \boldsymbol {E}^* = -\boldsymbol {\nabla } H$
in the one-form, and $q \boldsymbol {E}^* = -\boldsymbol {\nabla } H$![]() , with $H$
, with $H$![]() the Hamiltonian. Also, $B_{\|}^* = \hat {\boldsymbol {b}}\boldsymbol {\cdot } \boldsymbol {B}^*$
the Hamiltonian. Also, $B_{\|}^* = \hat {\boldsymbol {b}}\boldsymbol {\cdot } \boldsymbol {B}^*$![]() . At lowest order, these are equivalent to the original drift-kinetic equations of motion (Kruskal Reference Kruskal1962; Grad Reference Grad1966), with the curvature, $E\times B$
. At lowest order, these are equivalent to the original drift-kinetic equations of motion (Kruskal Reference Kruskal1962; Grad Reference Grad1966), with the curvature, $E\times B$![]() and grad-B drifts, but with small corrections that allow for exact conservation of energy, momenta and phase space volume. To avoid the dependence of these equations of motion on the time derivative of $A_{\|}$
and grad-B drifts, but with small corrections that allow for exact conservation of energy, momenta and phase space volume. To avoid the dependence of these equations of motion on the time derivative of $A_{\|}$![]() , certain codes (including ORB5) evolve $p = m v_{\|} + q A_{\|}$
, certain codes (including ORB5) evolve $p = m v_{\|} + q A_{\|}$![]() instead of $v_{\|}$
instead of $v_{\|}$![]() and thus move the perturbed field fully into the Hamiltonian.
and thus move the perturbed field fully into the Hamiltonian.
An important class of modified gyrokinetic Lagrangians move the plasma flow into the symplectic form (Sosenko, Bertrand & Decyk Reference Sosenko, Bertrand and Decyk2001; Dimits Reference Dimits2010; Duthoit et al. Reference Duthoit, Hahm and Wang2014). Although this does not lead to higher formal accuracy if the same orderings are retained, for long-wavelength perturbations the amplitude of the gyroangle-dependent terms (before the small coordinate shift) is much smaller than assumed by the ordering: this leads to a long-wavelength formulation which is better than might be expected and thus closer to drift kinetics (in an intermediate-length-scale regime, as noted by Duthoit et al. (Reference Duthoit, Hahm and Wang2014)). By formally taking advantage of this improvement as part of the ordering, one may derive extended schemes that simultaneously allow gyrokinetic-ordered and drift-kinetic-ordered perturbations (Dimits Reference Dimits2010; McMillan & Sharma Reference McMillan and Sharma2016). A major apparent obstacle is the appearance of time derivatives of the electric field in the dynamical equations, which requires a modified solution scheme (Sharma & McMillan Reference Sharma and McMillan2020). In the MHD-like approach explained later in this paper, this issue has a straightforward resolution.
3. Consistency of gyrokinetic equilibria with MHD equilibria
A well-known consistency issue in applied gyrokinetics is that the assumed background distributions ($f_0$![]() ) of ions and electrons have gyroaveraged charge that may not exactly sum to zero, consistent with a zero background electric field; given equal guiding-centre charges, the pullback transformation and gyroaveraging give rise to a free-charge separation, which is small, but the associated electric field may be significant. Global gyrokinetic codes normally ignore any net background charge (e.g. see the discussion after equation (17) in Jolliet et al. (Reference Jolliet, Bottino, Angelino, Hatzky, Tran, McMillan, Sauter, Appert, Idomura and Villard2007)).
) of ions and electrons have gyroaveraged charge that may not exactly sum to zero, consistent with a zero background electric field; given equal guiding-centre charges, the pullback transformation and gyroaveraging give rise to a free-charge separation, which is small, but the associated electric field may be significant. Global gyrokinetic codes normally ignore any net background charge (e.g. see the discussion after equation (17) in Jolliet et al. (Reference Jolliet, Bottino, Angelino, Hatzky, Tran, McMillan, Sauter, Appert, Idomura and Villard2007)).
As a preliminary to obtaining and implementing dynamical equations, I discuss here the electromagnetic extension of this, the correspondence between the currents implied by a gyrokinetic background distribution function (currents which appear in the gyrokinetic or drift-kinetic Ampère's law) and those of MHD (i.e. the currents that appear in Grad–Shafranov equilibria, and satisfy $\boldsymbol {\nabla } \times \boldsymbol {B} = \mu _0 \boldsymbol {J}$![]() ). Currents also appear in kinetic theories through direct motion of the guiding/gyrocentres, leading to accumulation of free charge; such currents are not necessarily equal to those that appear in the gyrokinetic/drift-kinetic Ampères law. The question is whether gyrokinetic distribution functions imply currents that agree with the MHD equilibria which are used to define the background field. Gyrokinetic formulations like ORB5 and GENE tend to only resolve perturbed currents (e.g. between equations (10) and (12) of Bottino et al. (Reference Bottino, Scott, Brunner, McMillan, Tran, Vernay, Villard, Jolliet, Hatzky and Peeters2010) the background term quietly disappears), but the perturbed currents depend on the equilibrium currents, when the plasma moves. Practically, this is particularly important for kink mode physics, where diamagnetic-drift-ordered parallel currents in the equilibrium lead to a driving force once the plasma is displaced. The currents associated with particle motion in drift kinetics/gyrokinetics may be obtained directly by taking real space moments (including the pullback), but I use a variational approach; Pfirsch (Reference Pfirsch1984) contains a complete variational derivation of the currents in a drift-kinetic system, and the form I obtain is similar. The derivation of Lee (Reference Lee2016) touched on several of the issues. I present a relatively simple kinetic equilibrium distribution function which is a solution to the unperturbed gyro-Vlasov–Maxwell equations, and whose first three moments match the MHD equilibrium up to the order of the diamagnetic currents. Neoclassical equilibria will also satisfy this consistency condition.
). Currents also appear in kinetic theories through direct motion of the guiding/gyrocentres, leading to accumulation of free charge; such currents are not necessarily equal to those that appear in the gyrokinetic/drift-kinetic Ampères law. The question is whether gyrokinetic distribution functions imply currents that agree with the MHD equilibria which are used to define the background field. Gyrokinetic formulations like ORB5 and GENE tend to only resolve perturbed currents (e.g. between equations (10) and (12) of Bottino et al. (Reference Bottino, Scott, Brunner, McMillan, Tran, Vernay, Villard, Jolliet, Hatzky and Peeters2010) the background term quietly disappears), but the perturbed currents depend on the equilibrium currents, when the plasma moves. Practically, this is particularly important for kink mode physics, where diamagnetic-drift-ordered parallel currents in the equilibrium lead to a driving force once the plasma is displaced. The currents associated with particle motion in drift kinetics/gyrokinetics may be obtained directly by taking real space moments (including the pullback), but I use a variational approach; Pfirsch (Reference Pfirsch1984) contains a complete variational derivation of the currents in a drift-kinetic system, and the form I obtain is similar. The derivation of Lee (Reference Lee2016) touched on several of the issues. I present a relatively simple kinetic equilibrium distribution function which is a solution to the unperturbed gyro-Vlasov–Maxwell equations, and whose first three moments match the MHD equilibrium up to the order of the diamagnetic currents. Neoclassical equilibria will also satisfy this consistency condition.
Let us vary the system Lagrangian $L_s$![]() (sum of (2.2) and (2.4)) with respect to $\boldsymbol {A}$
(sum of (2.2) and (2.4)) with respect to $\boldsymbol {A}$![]() to find the gyrokinetic Ampère's law. I vary $\boldsymbol {A}$
to find the gyrokinetic Ampère's law. I vary $\boldsymbol {A}$![]() by $\delta \boldsymbol {A}$
by $\delta \boldsymbol {A}$![]() and require
and require

where here (and throughout the paper) there is an implied sum over species that is omitted to simplify the expressions. Two terms on the right-hand side can be integrated by parts, assuming the field normal to the boundary is zero, and for arbitrary variations of $\delta \boldsymbol {A}$![]() this implies
this implies

and the terms on the right-hand side are identified as currents in the drift-kinetic Ampère's law. I define $\boldsymbol {J}_\textrm {mag}$![]() as the perpendicular current arising from the first term (in square brackets), $\boldsymbol {J}_\textrm {drift}$
as the perpendicular current arising from the first term (in square brackets), $\boldsymbol {J}_\textrm {drift}$![]() as the perpendicular current arising from the second term, $\boldsymbol {J}_\textrm {pol}$
as the perpendicular current arising from the second term, $\boldsymbol {J}_\textrm {pol}$![]() as the current arising from the third term and $J_{\|}$
as the current arising from the third term and $J_{\|}$![]() as the parallel current associated with this expression. This form (ignoring the fourth term on the right-hand side) is seen in early work on guiding-centre theory such as equation (11) of Sagdeyev et al. (Reference Sagdeyev, Kadomtsev, Rudakov and Vedyonov1958), but there are some important subtleties here in the volume element, and in the correspondence between the distribution function $f$
as the parallel current associated with this expression. This form (ignoring the fourth term on the right-hand side) is seen in early work on guiding-centre theory such as equation (11) of Sagdeyev et al. (Reference Sagdeyev, Kadomtsev, Rudakov and Vedyonov1958), but there are some important subtleties here in the volume element, and in the correspondence between the distribution function $f$![]() in standard $(\boldsymbol {X},\boldsymbol {v})$
in standard $(\boldsymbol {X},\boldsymbol {v})$![]() coordinates and in Littlejohn's modified guiding-centre variables. At the order of the diamagnetic drifts, and with weak flows, these currents reduce to the usual familiar parallel, curvature, gradient drift, magnetisation and polarisation currents.
coordinates and in Littlejohn's modified guiding-centre variables. At the order of the diamagnetic drifts, and with weak flows, these currents reduce to the usual familiar parallel, curvature, gradient drift, magnetisation and polarisation currents.
The variation of the field direction $\boldsymbol {b}$![]() in the symplectic term leads to the higher-order current in the fourth term on the right-hand side; the vorticity is small compared with the gyrofrequency, and is even in $v_{\|}$
in the symplectic term leads to the higher-order current in the fourth term on the right-hand side; the vorticity is small compared with the gyrofrequency, and is even in $v_{\|}$![]() , so that this term is the product of a drift-ordered vorticity and the small odd moments of $f$
, so that this term is the product of a drift-ordered vorticity and the small odd moments of $f$![]() , and thus ordered small compared with the other currents. In a complete fully nonlinear formulation, keeping this term would be required for exact conservation to hold, although a linear or delta-f code might simply replace $\boldsymbol {b}$
, and thus ordered small compared with the other currents. In a complete fully nonlinear formulation, keeping this term would be required for exact conservation to hold, although a linear or delta-f code might simply replace $\boldsymbol {b}$![]() with the unperturbed field $\boldsymbol {b}_0$
with the unperturbed field $\boldsymbol {b}_0$![]() in the Lagrangian (and thus conserve modified energies and momenta). Note the correspondence here to the additional magnetisation terms present in equation (63) of Pfirsch (Reference Pfirsch1984).
in the Lagrangian (and thus conserve modified energies and momenta). Note the correspondence here to the additional magnetisation terms present in equation (63) of Pfirsch (Reference Pfirsch1984).
Now consider the question of equilibrium currents, where the polarisation terms may be ignored. I consider first the so-called ‘global Maxwellian’ gyrokinetic particle distribution given by

which is a function only of the conserved quantities $\epsilon = \mu B + m v_{\parallel }^2/2$![]() and the canonical toroidal momentum $\varPsi _c = \varPsi + m F v_{\|}/ q B$
and the canonical toroidal momentum $\varPsi _c = \varPsi + m F v_{\|}/ q B$![]() (with $\varPsi$
(with $\varPsi$![]() the poloidal flux). This is a gyrokinetic equilibrium in the sense that $f$
the poloidal flux). This is a gyrokinetic equilibrium in the sense that $f$![]() is constant along unperturbed trajectories: it is therefore a solution to the gyro-Vlasov equation. In the small $\rho ^*$
is constant along unperturbed trajectories: it is therefore a solution to the gyro-Vlasov equation. In the small $\rho ^*$![]() limit this is a local isotropic Maxwellian with density $n$
limit this is a local isotropic Maxwellian with density $n$![]() and temperature $T$
and temperature $T$![]() (and pressure $p$
(and pressure $p$![]() ), but the use of a canonical momentum function leads to a correction, which is at next order just a shifted Maxwellian, with a net velocity in the parallel direction (the associated current is labelled $\boldsymbol {J}_{C}$
), but the use of a canonical momentum function leads to a correction, which is at next order just a shifted Maxwellian, with a net velocity in the parallel direction (the associated current is labelled $\boldsymbol {J}_{C}$![]() ). Higher-order $\rho ^*$
). Higher-order $\rho ^*$![]() effects will be ignored in the following analysis.
effects will be ignored in the following analysis.
Moments $\int \,\textrm {d}\boldsymbol {v} v^n f$![]() of the distribution are performed using $\textrm {d}\boldsymbol {v} = B_{\|}^* \,\textrm {d}\mu \,\textrm {d}v_{\|}$
of the distribution are performed using $\textrm {d}\boldsymbol {v} = B_{\|}^* \,\textrm {d}\mu \,\textrm {d}v_{\|}$![]() , and $B_{\|}^* = B + B.J \mu _0 m v_{\|}/ q B^2$
, and $B_{\|}^* = B + B.J \mu _0 m v_{\|}/ q B^2$![]() , leading to an additional non-zero contribution to the first $v_{\|}$
, leading to an additional non-zero contribution to the first $v_{\|}$![]() moment of the distribution that is a component of $J_{\|}$
moment of the distribution that is a component of $J_{\|}$![]() . This current may be evaluated as $\boldsymbol {J}_* = \beta \boldsymbol {b}\boldsymbol {b}\boldsymbol {\cdot }\boldsymbol {J} / 2$
. This current may be evaluated as $\boldsymbol {J}_* = \beta \boldsymbol {b}\boldsymbol {b}\boldsymbol {\cdot }\boldsymbol {J} / 2$![]() , with $\beta = p / (B^2/2 \mu _0)$
, with $\beta = p / (B^2/2 \mu _0)$![]() , for this equilibrium, to lowest non-vanishing order in $\rho ^*$
, for this equilibrium, to lowest non-vanishing order in $\rho ^*$![]() .
.
Some vector algebra suffices to show that these currents add up so that perpendicular currents are consistent with MHD equilibrium $\boldsymbol {J}_d + \boldsymbol {J}_* + \boldsymbol {J}_M = - \boldsymbol {\nabla } p \times \boldsymbol {B} / B^2$![]() . Note that both $\boldsymbol {J}_*$
. Note that both $\boldsymbol {J}_*$![]() and $\boldsymbol {J}_M$
and $\boldsymbol {J}_M$![]() have a parallel component, and these two components cancel; these components are small at low $\beta$
have a parallel component, and these two components cancel; these components are small at low $\beta$![]() , but otherwise drift-ordered like other equilibrium currents.
, but otherwise drift-ordered like other equilibrium currents.
The remaining parallel gyrokinetic currents should be consistent with the MHD parallel current $J_{\|}$![]() . The Grad–Shafranov equation implies $\boldsymbol {J} \boldsymbol {\cdot } \boldsymbol {b} = (\boldsymbol {\nabla } \times \boldsymbol {B}) \boldsymbol {\cdot } \boldsymbol {B} / \mu _0 B= F' B + F p'/B$
. The Grad–Shafranov equation implies $\boldsymbol {J} \boldsymbol {\cdot } \boldsymbol {b} = (\boldsymbol {\nabla } \times \boldsymbol {B}) \boldsymbol {\cdot } \boldsymbol {B} / \mu _0 B= F' B + F p'/B$![]() . In general
. In general
and this is a general property of equilibria that are local Maxwellian to lowest order. Since $J_C \neq J_{\|}$![]() , there must be an additional parallel current introduced in the gyrokinetic equilibrium. The comparison with the MHD expression requires an additional divergence-free parallel current, $J_{\|} \propto B$
, there must be an additional parallel current introduced in the gyrokinetic equilibrium. The comparison with the MHD expression requires an additional divergence-free parallel current, $J_{\|} \propto B$![]() , which may be introduced in the gyrokinetic equilibrium (without changing perpendicular currents at lowest order in $\rho ^*$
, which may be introduced in the gyrokinetic equilibrium (without changing perpendicular currents at lowest order in $\rho ^*$![]() ) by specifying
) by specifying

with
when the term in the square root is positive and $Q=0$![]() otherwise (i.e. for trapped particles) (Angelino et al. Reference Angelino, Bottino, Hatzky, Jolliet, Sauter, Tran and Villard2006). Here, $B_+$
otherwise (i.e. for trapped particles) (Angelino et al. Reference Angelino, Bottino, Hatzky, Jolliet, Sauter, Tran and Villard2006). Here, $B_+$![]() is the maximum value of $B$
is the maximum value of $B$![]() on the flux surface $\varPsi _c$
on the flux surface $\varPsi _c$![]() . This leads to a net flow in the passing particles. At the position of maximum $B_+$
. This leads to a net flow in the passing particles. At the position of maximum $B_+$![]() (inboard mid-plane for a typical up–down symmetric case) the mean parallel drift is simple to calculate, and equals $v_0$
(inboard mid-plane for a typical up–down symmetric case) the mean parallel drift is simple to calculate, and equals $v_0$![]() , so agreement with MHD requires $q n v_0 = F' B_+$
, so agreement with MHD requires $q n v_0 = F' B_+$![]() , when summed over species. It is simplest to just add this shift to the electron distribution, but to retain zero net mass flow, both ion and electron distributions may be shifted appropriately. The additional current is divergence-free (charge does not accumulate since $f$
, when summed over species. It is simplest to just add this shift to the electron distribution, but to retain zero net mass flow, both ion and electron distributions may be shifted appropriately. The additional current is divergence-free (charge does not accumulate since $f$![]() is a gyrokinetic equilibrium). Since it is divergence-free and entirely parallel (at lowest order), it matches the term $F' B$
is a gyrokinetic equilibrium). Since it is divergence-free and entirely parallel (at lowest order), it matches the term $F' B$![]() in the MHD parallel current on the full flux surface (not just where $B=B_+$
in the MHD parallel current on the full flux surface (not just where $B=B_+$![]() ).
).
Looking at the level of current in each plasma species, rather than overall equilibrium current, one can identify parallel currents associated with each plasma species, as a result of per-species zero-divergence motion: these Pfirsch–Schlüter currents originate from pressure gradients, and are not dominated by electrons. Although for large-scale motion it may suffice that the gyrokinetic equilibrium has the correct total, but not per-species, current, Finite Larmor Radius (FLR) effects (for example where fast particles are present) can lead to certain species being decoupled from the plasma motion: the dynamics may depend on which species is carrying the current.
Other gyrokinetic equilibria exist that reduce to local isotropic Maxwellians in the $\rho ^* \rightarrow 0$![]() limit, but this modified global Maxwellian is simple, used in existing codes and demonstrates the principle. A more physically motivated choice for the distribution would be to consider a neoclassical solution, which in the $\rho ^* \rightarrow 0$
limit, but this modified global Maxwellian is simple, used in existing codes and demonstrates the principle. A more physically motivated choice for the distribution would be to consider a neoclassical solution, which in the $\rho ^* \rightarrow 0$![]() limit also reduces to a local isotropic Maxwellian. The neoclassical solution is constrained to have the same zeroth, first and second moments of these distributions up to lowest non-vanishing order.
limit also reduces to a local isotropic Maxwellian. The neoclassical solution is constrained to have the same zeroth, first and second moments of these distributions up to lowest non-vanishing order.
Note that in practice global codes frequently use background distributions (usually a local Maxwellian) that are not equilibrium solution to the Vlasov equation. Usually this is a shifted Maxwellian, but ORB5 has also implemented a poloidally-constant shifted Maxwellian distribution (Hatzky et al. Reference Hatzky, Kleiber, Könies, Mishchenko, Borchardt, Bottino and Sonnendrücker2019).
4. Kinetic current components in a test equilibrium
A gyrokinetic equilibrium with a finite parallel current, consistent with the MHD currents, up to first order, was specified in (3.5). To demonstrate the magnitude of these currents, and test the implementation and diagnosis of various parallel kinetic currents in global gyrokinetic code, I examine a specific MHD equilibrium, and diagnose the associated gyrokinetic equilibrium. The circular-boundary pedestal-like equilibrium of Martin-Collar (Reference Martin-Collar2018) is used here. This has a moderate on-axis $\beta$![]() value of $7.4\,\%$
value of $7.4\,\%$![]() , but the narrow step in pressure at $r/a=0.5$
, but the narrow step in pressure at $r/a=0.5$![]() leads to a strong $\beta '$
leads to a strong $\beta '$![]() , so certain finite-$\beta$
, so certain finite-$\beta$![]() effects like the Pfirsch–Schlüter currents are quite pronounced. The ORB5 code takes information about the MHD equilibria and the per-species plasma profiles separately, and these were set to be consistent, with the overall plasma pressure in the profiles consistent with the MHD pressure profile.
effects like the Pfirsch–Schlüter currents are quite pronounced. The ORB5 code takes information about the MHD equilibria and the per-species plasma profiles separately, and these were set to be consistent, with the overall plasma pressure in the profiles consistent with the MHD pressure profile.
The code was run using the canonical Maxwellian described above, with the drift term $Q$![]() (equation (3.6)) added to the electron species which adds a divergence-free net parallel current. A relatively small value for $\rho ^* = a/R = 1/1600$
(equation (3.6)) added to the electron species which adds a divergence-free net parallel current. A relatively small value for $\rho ^* = a/R = 1/1600$![]() was chosen in order to approach the MHD limit: note that the simple canonical Maxwellian has relatively large finite-$\rho ^*$
was chosen in order to approach the MHD limit: note that the simple canonical Maxwellian has relatively large finite-$\rho ^*$![]() modifications (Angelino et al. Reference Angelino, Bottino, Hatzky, Jolliet, Sauter, Tran and Villard2006).
modifications (Angelino et al. Reference Angelino, Bottino, Hatzky, Jolliet, Sauter, Tran and Villard2006).
The ORB5 code diagnoses the equilibrium parallel momentum for each species on a set of bins in the $(r,\chi )$![]() plane by determining the integral $\int \,\textrm {d}\boldsymbol {Z} v_{\|} f$
plane by determining the integral $\int \,\textrm {d}\boldsymbol {Z} v_{\|} f$![]() : this is normalised by dividing by the bin volume to find a mean value $n\langle v \rangle$
: this is normalised by dividing by the bin volume to find a mean value $n\langle v \rangle$![]() in code units $n_0 c_s$
in code units $n_0 c_s$![]() . The associated parallel current is then constructed by multiplying by the species charge and summing. This includes the $J_*$
. The associated parallel current is then constructed by multiplying by the species charge and summing. This includes the $J_*$![]() current described above, as explicit evaluations of $\textrm {d}\boldsymbol {Z}$
current described above, as explicit evaluations of $\textrm {d}\boldsymbol {Z}$![]() involve $B^*$
involve $B^*$![]() . Density plots of the currents on the poloidal cross-section are constructed, as predicted by MHD equilibrium (figure 1a) and as diagnosed from the gyrokinetic code (figure 1b); visually these are essentially identical except for the noise resulting from Monte Carlo sampling. Note that for this equilibrium the Pfirsch–Schlüter currents almost cancel those prescribed via $F$
. Density plots of the currents on the poloidal cross-section are constructed, as predicted by MHD equilibrium (figure 1a) and as diagnosed from the gyrokinetic code (figure 1b); visually these are essentially identical except for the noise resulting from Monte Carlo sampling. Note that for this equilibrium the Pfirsch–Schlüter currents almost cancel those prescribed via $F$![]() . On line plots (figure 2), it is clear that the gyrokinetic code is actually resolving the sum of $J_{\|}$
. On line plots (figure 2), it is clear that the gyrokinetic code is actually resolving the sum of $J_{\|}$![]() and $J_*$
and $J_*$![]() . Since $J_*$
. Since $J_*$![]() is smaller by a factor of $\beta /2$
is smaller by a factor of $\beta /2$![]() , these currents are relatively small here and for conventional tokamaks; for high-$\beta$
, these currents are relatively small here and for conventional tokamaks; for high-$\beta$![]() spherical tokamaks these currents will be comparable, however, to MHD currents.
spherical tokamaks these currents will be comparable, however, to MHD currents.

Figure 1. (a) Parallel current density ($\textrm {A}\,\textrm {m}^{-2}$![]() ) in the circular-boundary MHD equilibrium. (b) Parallel current density ($\textrm {A}\,\textrm {m}^{-2}$
) in the circular-boundary MHD equilibrium. (b) Parallel current density ($\textrm {A}\,\textrm {m}^{-2}$![]() ) in the kinetic equilibrium distribution, calculated using markers.
) in the kinetic equilibrium distribution, calculated using markers.

Figure 2. Parallel current density versus radius $R$![]() in the circular-boundary MHD equilibrium on the outboard mid-plane. The black, red and blue curves represent the MHD parallel current $J_{\|}$
in the circular-boundary MHD equilibrium on the outboard mid-plane. The black, red and blue curves represent the MHD parallel current $J_{\|}$![]() , $J_* + J_{\|}$
, $J_* + J_{\|}$![]() and the output of the parallel current diagnostic in the gyrokinetic code (ORB5) respectively.
and the output of the parallel current diagnostic in the gyrokinetic code (ORB5) respectively.
5. Time-evolution equations for dynamical drift kinetics
The guiding-centre Vlasov equation for these drift-kinetic equations is
with the equations of motion (2.7).
If quasi-neutrality is not assumed, so that light waves are allowed, then both $\boldsymbol {B}$![]() and $\boldsymbol {E}$
and $\boldsymbol {E}$![]() are naturally dynamical quantities, and since the currents (through the polarisation drift) involve derivatives of $\boldsymbol {E}$
are naturally dynamical quantities, and since the currents (through the polarisation drift) involve derivatives of $\boldsymbol {E}$![]() one has direct time-evolution equations for these fields (Morrison Reference Morrison2013) (assuming certain inverses may be found). However, sub-gyrofrequency models usually consider the low-frequency (Darwin) limit assuming quasi-neutrality, so the appearance of time derivatives of the electric field in the field equations, through polarisation, is perhaps surprising. I show how one may nevertheless directly write down an intuitively appealing set of plasma dynamical equations in this limit.
one has direct time-evolution equations for these fields (Morrison Reference Morrison2013) (assuming certain inverses may be found). However, sub-gyrofrequency models usually consider the low-frequency (Darwin) limit assuming quasi-neutrality, so the appearance of time derivatives of the electric field in the field equations, through polarisation, is perhaps surprising. I show how one may nevertheless directly write down an intuitively appealing set of plasma dynamical equations in this limit.
In the Darwin limit, Ampère's law, from (3.2), is of the form
where $\boldsymbol {J}_\textrm {drift}$![]() , $\boldsymbol {J}_\textrm {mag}$
, $\boldsymbol {J}_\textrm {mag}$![]() and $J_{\|}$
and $J_{\|}$![]() , as defined earlier, may be determined from the distribution function and the magnetic and electric fields. This may be cast as a MHD momentum equation by taking the cross product with the magnetic field; $\boldsymbol {J}_\textrm {pol}$
, as defined earlier, may be determined from the distribution function and the magnetic and electric fields. This may be cast as a MHD momentum equation by taking the cross product with the magnetic field; $\boldsymbol {J}_\textrm {pol}$![]() leads to the acceleration term. Since the time derivative of $E_{\|}$
leads to the acceleration term. Since the time derivative of $E_{\|}$![]() does not enter directly here, it is not a dynamical quantity that is directly time evolved (or needed as an initial condition). Ampère's law may be used to solve for $\boldsymbol {J}_\textrm {pol}$
does not enter directly here, it is not a dynamical quantity that is directly time evolved (or needed as an initial condition). Ampère's law may be used to solve for $\boldsymbol {J}_\textrm {pol}$![]() . The complete polarisation term $\boldsymbol {J}_\textrm {pol}$
. The complete polarisation term $\boldsymbol {J}_\textrm {pol}$![]() is shown in Appendix A, but when Boussinesq-type polarisation is used we have
is shown in Appendix A, but when Boussinesq-type polarisation is used we have
In this case we may solve for perpendicular acceleration:
Instead of evolving the perpendicular velocity or $\boldsymbol {E}_\perp$![]() , a vorticity equation may be found by taking the perpendicular divergence, as in Miyato et al. (Reference Miyato, Scott, Strintzi and Tokuda2009), to obtain equations which are in a form related to standard fluid models like Hasegawa–Mima (Hasegawa & Mima Reference Hasegawa and Mima1978). In standard gyrokinetic orderings, the rotational part of this equation, found by taking the curl, leads to a magnetic compression equation, where, in the quasi-static limit, the perpendicular plasma pressure is balanced against magnetic pressure, to find $B_{\|}$
, a vorticity equation may be found by taking the perpendicular divergence, as in Miyato et al. (Reference Miyato, Scott, Strintzi and Tokuda2009), to obtain equations which are in a form related to standard fluid models like Hasegawa–Mima (Hasegawa & Mima Reference Hasegawa and Mima1978). In standard gyrokinetic orderings, the rotational part of this equation, found by taking the curl, leads to a magnetic compression equation, where, in the quasi-static limit, the perpendicular plasma pressure is balanced against magnetic pressure, to find $B_{\|}$![]() . At system scale the perpendicular and parallel components do not completely decouple, and the rotational part of the equation contains motion associated with magnetic compression that should be retained to correctly resolve large-scale MHD-like modes. However, in a practical implementation, one would usually not want to retain fast waves at the gyroscale, so this splitting may still be useful as part of an implicit solve.
. At system scale the perpendicular and parallel components do not completely decouple, and the rotational part of the equation contains motion associated with magnetic compression that should be retained to correctly resolve large-scale MHD-like modes. However, in a practical implementation, one would usually not want to retain fast waves at the gyroscale, so this splitting may still be useful as part of an implicit solve.
Since this equation is in the same form as the perpendicular component of the MHD momentum law, the relationship to hybrid MHD formalisms is straightforward; in both current-coupling and pressure-coupling versions of kinetic MHD (Burby & Tronci Reference Burby and Tronci2017), the kinetic species give rise to additional forces in the momentum law (through $J \times B$![]() forces or pressure forces), and this drift-kinetic formulation is equivalent to a current-coupling scheme for the kinetic currents of all the species, including the bulk ions and electrons.
forces or pressure forces), and this drift-kinetic formulation is equivalent to a current-coupling scheme for the kinetic currents of all the species, including the bulk ions and electrons.
The scheme also needs to determine $E_{\|}$![]() , which is found from the time derivative of the parallel component of Ampère's law, as
, which is found from the time derivative of the parallel component of Ampère's law, as
and using $\partial \boldsymbol {B} / \partial t = - \boldsymbol {\nabla } \times \boldsymbol {E}$![]() ,
,
with an explicit sum over species $s$![]() and where the remaining parallel forces in the momentum equation (e.g. convective momentum transport and mirror forces) have been denoted as $F_{s\|}$
and where the remaining parallel forces in the momentum equation (e.g. convective momentum transport and mirror forces) have been denoted as $F_{s\|}$![]() . Collisional friction would be also be expected to appear in $F_{s\|}$
. Collisional friction would be also be expected to appear in $F_{s\|}$![]() in a more complete theory (Sugama, Matsuoka & Nunami Reference Sugama, Matsuoka and Nunami2022). The right-hand side is normally dominated by the electron contribution due to the low electron mass. An important component of the time dependence of the parallel current is the first moment of the distribution function:
in a more complete theory (Sugama, Matsuoka & Nunami Reference Sugama, Matsuoka and Nunami2022). The right-hand side is normally dominated by the electron contribution due to the low electron mass. An important component of the time dependence of the parallel current is the first moment of the distribution function:
and the first term may be approximately integrated by parts, with $\dot {v_{\|}} = F_{\|}/m + q E_{\|}/m$![]() and the volume element not depending at lowest order on $v_{\|}$
and the volume element not depending at lowest order on $v_{\|}$![]() , giving
, giving
where the second-last term would cancel with a term arising from parallel motion and the last term is a ponderomotive effect (also found in Morrison Reference Morrison2013) which does not appear when the Boussinesq-type polarisation is made in the Lagrangian. I do not explicitly evaluate the remaining terms that are independent of $E_{\|}$![]() individually: for practical computational evaluation it might be less complicated to use a numerical derivative $[J_{\|}(t+\delta t) - J_{\|}(t)]/ \delta t$
individually: for practical computational evaluation it might be less complicated to use a numerical derivative $[J_{\|}(t+\delta t) - J_{\|}(t)]/ \delta t$![]() of the first moment of the distribution function (while splitting out the effect of $E_{\|}$
of the first moment of the distribution function (while splitting out the effect of $E_{\|}$![]() ), since Vlasov's equation is in any case being solved, and this could be used to ensure consistency.
), since Vlasov's equation is in any case being solved, and this could be used to ensure consistency.
Practical use of (5.6) requires solution for $E_{\|}$![]() . A simplification is obtained by observing that on scales $L$
. A simplification is obtained by observing that on scales $L$![]() longer than the electron skin depth $d$
longer than the electron skin depth $d$![]() , the dependence on $E_{\|}$
, the dependence on $E_{\|}$![]() is largely through the scalar term on the right-hand side, which is dominant by a factor of $(L/d)^2$
is largely through the scalar term on the right-hand side, which is dominant by a factor of $(L/d)^2$![]() over the left-hand side, and this provides a simple practical iterative method for solving this equation for $E_{\|}$
over the left-hand side, and this provides a simple practical iterative method for solving this equation for $E_{\|}$![]() (because of the uniform dominance of the scalar term, the nullspace of the linear operator associated with $E_{\|}$
(because of the uniform dominance of the scalar term, the nullspace of the linear operator associated with $E_{\|}$![]() is trivial, so this should also, in the limit, be a unique solution). Although this also captures the usual transition in electron response below the skin depth, the drift-kinetic theory is of course only valid above the ion gyroscale, which is normally much larger than the electron skin depth. In this MHD-ordered theory, $E_{\perp }$
is trivial, so this should also, in the limit, be a unique solution). Although this also captures the usual transition in electron response below the skin depth, the drift-kinetic theory is of course only valid above the ion gyroscale, which is normally much larger than the electron skin depth. In this MHD-ordered theory, $E_{\perp }$![]() is larger than $E_{\|}$
is larger than $E_{\|}$![]() and the $\boldsymbol {E}_{\perp }$
and the $\boldsymbol {E}_{\perp }$![]() term is required to ensure that Ampère's law is satisfied. The parallel electric field is thus related to the inductive perpendicular electric field and the parallel forces (including collisional resistivity). That is, this is a kinetically modified Ohm's law, which reduces to $E_{\|}=0$
term is required to ensure that Ampère's law is satisfied. The parallel electric field is thus related to the inductive perpendicular electric field and the parallel forces (including collisional resistivity). That is, this is a kinetically modified Ohm's law, which reduces to $E_{\|}=0$![]() in the MHD limit. The departure from typical kinetic MHD approaches here is that $E_{\|}$
in the MHD limit. The departure from typical kinetic MHD approaches here is that $E_{\|}$![]() is explicitly calculated via the particle drift-kinetic equations; the kinetic origin of a finite parallel electric field is a central aspect of drift-wave instability theory, so retaining this is essential for joint treatment of drift-wave microinstability and MHD-related dynamics. Note that simply approximating $E_{\|}=0$
is explicitly calculated via the particle drift-kinetic equations; the kinetic origin of a finite parallel electric field is a central aspect of drift-wave instability theory, so retaining this is essential for joint treatment of drift-wave microinstability and MHD-related dynamics. Note that simply approximating $E_{\|}=0$![]() would not be adequate where the parallel currents are updated directly as a result of solution of the gyrokinetic Vlasov equation, so an explicit calculation of the small $E_{\|}$
would not be adequate where the parallel currents are updated directly as a result of solution of the gyrokinetic Vlasov equation, so an explicit calculation of the small $E_{\|}$![]() or direct enforcement of current consistency is required.
or direct enforcement of current consistency is required.
With these field equations, for a specified distribution function, $f$![]() , $\boldsymbol {B}$
, $\boldsymbol {B}$![]() and $\boldsymbol {E}_{\perp }$
and $\boldsymbol {E}_{\perp }$![]() , one may calculate $\boldsymbol {E}_{\|}$
, one may calculate $\boldsymbol {E}_{\|}$![]() using (5.6), use the momentum equation to find the time derivative of $\boldsymbol {E}_{\perp }$
using (5.6), use the momentum equation to find the time derivative of $\boldsymbol {E}_{\perp }$![]() , use Faraday's law to find the time derivative of the magnetic field and use Vlasov's equation (5.1) to find the time derivative of the distribution function, which is sufficient to specify the time evolution of all the dynamical quantities, $f$
, use Faraday's law to find the time derivative of the magnetic field and use Vlasov's equation (5.1) to find the time derivative of the distribution function, which is sufficient to specify the time evolution of all the dynamical quantities, $f$![]() , $\boldsymbol {B}$
, $\boldsymbol {B}$![]() and $\boldsymbol {E}_{\perp }$
and $\boldsymbol {E}_{\perp }$![]() . The equations are derived via a variational approach, so have associated momentum and energy conservation laws, as long as the simplifications are made consistently; for example, if a linearised polarisation equation is used then the equations of motion used in calculating the Vlasov equation should not contain a ponderomotive term.
. The equations are derived via a variational approach, so have associated momentum and energy conservation laws, as long as the simplifications are made consistently; for example, if a linearised polarisation equation is used then the equations of motion used in calculating the Vlasov equation should not contain a ponderomotive term.
The overall method is very closely related to a maximal version of kinetic MHD that captures the full guiding-centre kinetics of each species, but also the full-kinetic parallel Ohms’ law. A kinetic-MHD-type scheme would explicitly evolve fluid equations for each species, unlike a direct kinetic scheme, but of course with a kinetic closure this should be equivalent. As a result, it may practically be easier to extend kinetic MHD frameworks to capture the additional physics required rather than a gyrokinetic code. This model has been presented in a somewhat symbolic and general form, and it might practically be useful to make various approximations; where these are made in the system Lagrangian before variation (e.g. not keeping the full-$f$![]() polarisation term and fixing the magnetic field variation in that term) the scheme will still be conservative. As usual, without any further approximations, and with appropriate boundary conditions, the system conserves the total system energy, as well as the particle canonical momentum (electromagnetic field momentum is zero in the Darwin limit).
polarisation term and fixing the magnetic field variation in that term) the scheme will still be conservative. As usual, without any further approximations, and with appropriate boundary conditions, the system conserves the total system energy, as well as the particle canonical momentum (electromagnetic field momentum is zero in the Darwin limit).
The appearance of $\boldsymbol {E}_{\perp }$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() as dynamical quantities (equivalent to five scalar fields), unlike in conventional gyrokinetics, where all of the fields may be found from the instantaneous distribution function, is related to some extra degrees of freedom of the system, as well as certain constraints on the distribution function and fields:
as dynamical quantities (equivalent to five scalar fields), unlike in conventional gyrokinetics, where all of the fields may be found from the instantaneous distribution function, is related to some extra degrees of freedom of the system, as well as certain constraints on the distribution function and fields:
(i) The fast magnetoacoustic mode is included: this requires two additional degrees of freedom.
(ii) The distribution functions must satisfy quasi-neutrality.
(iii) Field $\boldsymbol {B}$
 must be divergence-free.
must be divergence-free.(iv) The parallel component of Ampère's law (which is not a dynamical equation) must always be satisfied.
The last three of these statements are constraints which hold automatically for the time-evolved state if they are initially satisfied; it may be desirable to impose them explicitly via a divergence-cleaning type of approach or an appropriate projection. In other words, some of the quantities that appear in dynamical variables are in fact not additional degrees of freedom of the system. This is familiar from, for example, standard theory of particles interacting with electromagnetic fields, where a field $\boldsymbol {B}$![]() that solves Maxwell's equations remains divergence-free if it is initialised correctly.
that solves Maxwell's equations remains divergence-free if it is initialised correctly.
The inclusion of fast wave dynamics is appropriate for this system-scale MHD-ordered theory, unlike in local gyrokinetics. Ion-Larmor-radius-scale fast modes oscillate at or above the gyrofrequency (for $\beta \lesssim 1$![]() ) which is $O(1/\epsilon _E)$
) which is $O(1/\epsilon _E)$![]() times faster than frequencies of drift waves, so it is sufficient to order fast modes out of local gyrokinetic theory by treating magnetic compression as being in a quasi-static equilibrium. But system-scale fast modes have frequencies of order $v_{A}/a$
times faster than frequencies of drift waves, so it is sufficient to order fast modes out of local gyrokinetic theory by treating magnetic compression as being in a quasi-static equilibrium. But system-scale fast modes have frequencies of order $v_{A}/a$![]() , which is comparable to drift frequencies if $\beta$
, which is comparable to drift frequencies if $\beta$![]() is of order unity (for numerical purposes some semi-implicit timestepping would probably be desirable to also efficiently handle gyroradius-scale modes).
is of order unity (for numerical purposes some semi-implicit timestepping would probably be desirable to also efficiently handle gyroradius-scale modes).
As in related electrostatic formalisms (Dimits Reference Dimits2010; Sharma & McMillan Reference Sharma and McMillan2015), the electric field appears as a dynamical variable in the gyrokinetic theory even though it is not a dynamical variable in a low-frequency Darwin–Maxwell–Vlasov system, where the displacement current has been neglected, if fast waves have also been ignored. In this electromagnetic system, the appearance of the time derivative of the electric field seems more natural. One way to formally motivate the solution method and formalism is to consider the $\epsilon _0 \rightarrow 0$![]() limit. In the full Maxwell–Vlasov system $\boldsymbol {E}$
limit. In the full Maxwell–Vlasov system $\boldsymbol {E}$![]() is naturally a dynamical variable, and as one takes $\epsilon _0 \rightarrow 0$
is naturally a dynamical variable, and as one takes $\epsilon _0 \rightarrow 0$![]() the light waves increase in frequency; the dynamics of interest do not, so one is interested in retaining only the low-frequency dynamics and even though one solves for these additional degrees of freedom in our system, they may treated in the quasi-static limit.
the light waves increase in frequency; the dynamics of interest do not, so one is interested in retaining only the low-frequency dynamics and even though one solves for these additional degrees of freedom in our system, they may treated in the quasi-static limit.
An advantage of a formulation in terms of $\boldsymbol {E}$![]() and $\boldsymbol {B}$
and $\boldsymbol {B}$![]() rather than vector and scalar potentials is that it allows direct separation of the parallel component of the electric field, which is formally small compared with the perpendicular component. In a potential-based formulation $\partial A_{\|}/\partial t$
rather than vector and scalar potentials is that it allows direct separation of the parallel component of the electric field, which is formally small compared with the perpendicular component. In a potential-based formulation $\partial A_{\|}/\partial t$![]() and $\boldsymbol {\nabla } \phi$
and $\boldsymbol {\nabla } \phi$![]() are required to almost cancel to represent MHD-like motion (Hatzky et al. Reference Hatzky, Kleiber, Könies, Mishchenko, Borchardt, Bottino and Sonnendrücker2019), which is difficult to ensure exactly in a discretised form (this is an additional and more strict requirement on cancellation on top of the usual ‘cancellation problem’ (Reynders Reference Reynders1992) and exists even in symplectic formulations).
are required to almost cancel to represent MHD-like motion (Hatzky et al. Reference Hatzky, Kleiber, Könies, Mishchenko, Borchardt, Bottino and Sonnendrücker2019), which is difficult to ensure exactly in a discretised form (this is an additional and more strict requirement on cancellation on top of the usual ‘cancellation problem’ (Reynders Reference Reynders1992) and exists even in symplectic formulations).
6. Solving the field equations in a periodic 2-D system
To explore the use of drift kinetics to study plasma dynamics, I implement a simple drift-kinetic solver in a 2-D periodic geometry. The aim is mostly to illustrate as a proof-of-principle that the above field equations may be directly solved, and to act as a simple testbed for eventual complete testing and comparison of drift-kinetic/gyrokinetic models.
To demonstrate this in the simplest possible setting, a 2-D periodic slab domain is chosen, of size $(L_x, L_y)$![]() in the $(x,y)$
in the $(x,y)$![]() plane. An initially MHD-equilibrium configuration is perturbed by adding a bulk plasma velocity. Because of the simplicity of the Cartesian geometry, direct numerical evaluation is very straightforward, without the complexity of curvilinear coordinates or boundaries. Moderately complicated MHD equilibria, however, still exist in this simple setting, with curvature and field strength varying along field lines. For equilibrium, the large-aspect-ratio limit of the Grad–Shafranov equation gives
plane. An initially MHD-equilibrium configuration is perturbed by adding a bulk plasma velocity. Because of the simplicity of the Cartesian geometry, direct numerical evaluation is very straightforward, without the complexity of curvilinear coordinates or boundaries. Moderately complicated MHD equilibria, however, still exist in this simple setting, with curvature and field strength varying along field lines. For equilibrium, the large-aspect-ratio limit of the Grad–Shafranov equation gives
and
Linearising these equations is possible if $p + B^2 = c + d \psi + e \psi ^2$![]() , and the solutions are plane waves $\psi = \psi _0 \sin (\boldsymbol {k} \boldsymbol {\cdot } \boldsymbol {R})$
, and the solutions are plane waves $\psi = \psi _0 \sin (\boldsymbol {k} \boldsymbol {\cdot } \boldsymbol {R})$![]() , with $\boldsymbol {k}$
, with $\boldsymbol {k}$![]() quantised due the boundary conditions. Complex configurations are possible by superimposing several plane wave solutions in periodic configurations where multiple waves with the same $|k|$
quantised due the boundary conditions. Complex configurations are possible by superimposing several plane wave solutions in periodic configurations where multiple waves with the same $|k|$![]() exist, e.g. $L_x=L_y$
exist, e.g. $L_x=L_y$![]() ; I select ${L_x = L_y / \sqrt {3}}$
; I select ${L_x = L_y / \sqrt {3}}$![]() which allows waves in three different directions.
which allows waves in three different directions.
I take mass, charge, density and temperature reference values $m_R$![]() , $q_r$
, $q_r$![]() , $n_R$
, $n_R$![]() and $T_r$
and $T_r$![]() respectively. The velocity unit is $v_{R} = (T_{R}/m_{R})^{1/2}$
respectively. The velocity unit is $v_{R} = (T_{R}/m_{R})^{1/2}$![]() . The field reference value is $B_R^2 = \mu _0 n_{R} m_{R} v_{R}^2$
. The field reference value is $B_R^2 = \mu _0 n_{R} m_{R} v_{R}^2$![]() . The length reference is $\rho _{R} = m_{R} v_{R} / q_{R} B_{R}$
. The length reference is $\rho _{R} = m_{R} v_{R} / q_{R} B_{R}$![]() .
.
For this case, ion mass and charge are $m_i = m_{R}, q_i = q_{R}$![]() and electron mass and charge $m_e = m_R/4000$
and electron mass and charge $m_e = m_R/4000$![]() , $q_e = -q_{R}$
, $q_e = -q_{R}$![]() . A uniform initial plasma density is chosen as $n = n_{R}$
. A uniform initial plasma density is chosen as $n = n_{R}$![]() . The box size is $(L_x, L_y) = (100, 100 \times 3^{1/2}) \rho _R$
. The box size is $(L_x, L_y) = (100, 100 \times 3^{1/2}) \rho _R$![]() . I choose
. I choose

and $(B_z/B_{R})^2 = 10 + (4 {\rm \pi}/L_y)^2 \psi ^2 /2$![]() . With $p/(n_{R} T_{R}) = 1.0 + (4 {\rm \pi}/L_y)^2 \psi ^2 / 4$
. With $p/(n_{R} T_{R}) = 1.0 + (4 {\rm \pi}/L_y)^2 \psi ^2 / 4$![]() , this satisfies the slab Grad–Shafranov equation. Ions are chosen to be cold with $T_i =0$
, this satisfies the slab Grad–Shafranov equation. Ions are chosen to be cold with $T_i =0$![]() , and the electron temperature is set so that $n T_e = p$
, and the electron temperature is set so that $n T_e = p$![]() . Flux $\psi$
. Flux $\psi$![]() is plotted in figure 3(a).
is plotted in figure 3(a).

Figure 3. (a) Magnetic flux $\psi$![]() and (b) $\partial v_{\|} /\partial t$
and (b) $\partial v_{\|} /\partial t$![]() in the $(x, y)$
in the $(x, y)$![]() plane for the 2-D periodic model drift-kinetic problem.
plane for the 2-D periodic model drift-kinetic problem.
The initial perpendicular electric field is chosen as
giving rise to an initial bulk plasma velocity largely in the $y$![]() direction.
direction.
This configuration is used to evaluate the resulting parallel electric field in this configuration, and the time derivatives of the magnetic field and perpendicular electric field (the Vlasov equations were not solved). The outline is essentially equivalent to solving a kinetically modified MHD equation. First, the equation for the time derivative (5.4) is solved using the Boussinesq-type polarisation to find the perpendicular acceleration of the plasma. Then the parallel current is evaluated using (5.6): we have approximated the non-electric parallel force $F_{\|} = 0$![]() , as the configuration is initially in equilibrium, aside from the electric field. For this configuration, the rate of change of electron parallel velocity is plotted in figure 3(b). The parallel electric field is then evaluated using (5.6). We also have the rate of change of the magnetic field, from the induction equation. Together, this would be sufficient information to evaluate the drift-kinetic equations of motion.
, as the configuration is initially in equilibrium, aside from the electric field. For this configuration, the rate of change of electron parallel velocity is plotted in figure 3(b). The parallel electric field is then evaluated using (5.6). We also have the rate of change of the magnetic field, from the induction equation. Together, this would be sufficient information to evaluate the drift-kinetic equations of motion.
7. Conclusions
The links between various plasma models can appear somewhat mysterious. Unlike in a neutral fluid model, plasma kinetic momentum is normally re-expressed in terms of perpendicular electric field at low frequency, and there are various ways to rewrite perpendicular plasma force balance. For example, vorticity equations and vector force balance relations look superficially very different, but have a simple relationship to each other. We sometimes see the (somewhat surprising) appearance of the time derivative of the electric field in certain gyrokinetic theories, even in the Darwin (quasi-neutral) limit, where it is absent from Maxwell's equations; we argue that a conceptually simple way to approach this is to retain the full Mawxwell's equations, derive the resulting gyrokinetic equations of motion and field equations and then to formally consider the limit where $\epsilon _0 \rightarrow 0$![]() . This also yields the usual perpendicular pressure balance relation (at short wavelength) or allows retaining full magnetosonic motion at long wavelength.
. This also yields the usual perpendicular pressure balance relation (at short wavelength) or allows retaining full magnetosonic motion at long wavelength.
The motivation here is to allow consistent direct gyrokinetic computation of system-scale modes, particularly MHD-related modes, in conjunction with gyroscale dynamics. As certain gyrokinetic theories directly reduce to drift-kinetic theory at long wavelength (McMillan & Sharma Reference McMillan and Sharma2016), we can begin to approach this by studying the solution of drift-kinetic equations. Although drift-kinetic theory has long been known to be compatible with standard fluid formulations like MHD in appropriate limits, it is seldom used by itself in a Vlasov–Maxwell solution, and some care is needed to define appropriate equilibrium distribution functions, and in evaluating the parallel currents from drift kinetics. These questions were systematically approached by using a variational formalism. The drift-kinetic model is most easily solved by direct time evolution in a manner very much analogous to hybrid/kinetic MHD systems, with certain modifications that correspond to additional kinetic physics content.
It is important to be able to rapidly test what kinds of theory models are implementable as computational tools. The simple periodic problem presented here should allow various aspects of generalised gyrokinetic theory to be tested in non-trivial geometry, including equilibrium and wave physics. We have also defined a simple gyrokinetic equilibrium distribution function with currents that is consistent with the underlying MHD equilibrium; this may be useful for gyrokinetic simulation of large-scale current-driven modes.
Acknowledgements
Editor Paolo Ricci thanks the referees for their advice in evaluating this article.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200 – EUROfusion). Views and opinions expressed are however those of the author only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. We acknowledge funding from the UK EPSRC via grant EP/R034737/1.
Declaration of interests
The author reports no conflict of interest.
Appendix A. Perpendicular momentum equation
The perpendicular part of Ampère's law (which may be regarded as a perpendicular momentum equation) is
and the left-hand side may be evaluated directly as
and

so that overall
and we have additional terms that ensure that $E_{\perp }$![]() remains perpendicular to the changing magnetic field direction and that account for the change in polarisation with time due to field strength evolution. The density evolution term can, as with the parallel current evolution term, be evaluated via the Vlasov equation, which does not depend on $\partial \boldsymbol {E}/\partial t$
remains perpendicular to the changing magnetic field direction and that account for the change in polarisation with time due to field strength evolution. The density evolution term can, as with the parallel current evolution term, be evaluated via the Vlasov equation, which does not depend on $\partial \boldsymbol {E}/\partial t$![]() directly, and the density moment is insensitive to the dependence on $E_{\|}$
directly, and the density moment is insensitive to the dependence on $E_{\|}$![]() .
.