No CrossRef data available.
Article contents
COUNTABLE LENGTH EVERYWHERE CLUB UNIFORMIZATION
Published online by Cambridge University Press: 21 November 2022
Abstract
Assume 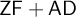 $\mathsf {ZF} + \mathsf {AD}$ and all sets of reals are Suslin. Let
$\mathsf {ZF} + \mathsf {AD}$ and all sets of reals are Suslin. Let 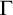 $\Gamma $ be a pointclass closed under
$\Gamma $ be a pointclass closed under 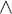 $\wedge $,
$\wedge $, 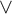 $\vee $,
$\vee $, 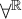 $\forall ^{\mathbb {R}}$, continuous substitution, and has the scale property. Let
$\forall ^{\mathbb {R}}$, continuous substitution, and has the scale property. Let 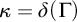 $\kappa = \delta (\Gamma )$ be the supremum of the length of prewellorderings on
$\kappa = \delta (\Gamma )$ be the supremum of the length of prewellorderings on 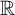 $\mathbb {R}$ which belong to
$\mathbb {R}$ which belong to 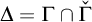 $\Delta = \Gamma \cap \check \Gamma $. Let
$\Delta = \Gamma \cap \check \Gamma $. Let 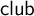 $\mathsf {club}$ denote the collection of club subsets of
$\mathsf {club}$ denote the collection of club subsets of 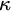 $\kappa $. Then the countable length everywhere club uniformization holds for
$\kappa $. Then the countable length everywhere club uniformization holds for 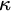 $\kappa $: For every relation
$\kappa $: For every relation 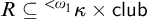 $R \subseteq {}^{<{\omega _1}}\kappa \times \mathsf {club}$ with the property that for all
$R \subseteq {}^{<{\omega _1}}\kappa \times \mathsf {club}$ with the property that for all 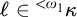 $\ell \in {}^{<{\omega _1}}\kappa $ and clubs
$\ell \in {}^{<{\omega _1}}\kappa $ and clubs 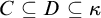 $C \subseteq D \subseteq \kappa $,
$C \subseteq D \subseteq \kappa $, 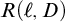 $R(\ell ,D)$ implies
$R(\ell ,D)$ implies 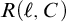 $R(\ell ,C)$, there is a uniformization function
$R(\ell ,C)$, there is a uniformization function 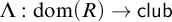 $\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$ with the property that for all
$\Lambda : \mathrm {dom}(R) \rightarrow \mathsf {club}$ with the property that for all 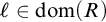 $\ell \in \mathrm {dom}(R)$,
$\ell \in \mathrm {dom}(R)$, 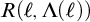 $R(\ell ,\Lambda (\ell ))$. In particular, under these assumptions, for all
$R(\ell ,\Lambda (\ell ))$. In particular, under these assumptions, for all 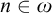 $n \in \omega $,
$n \in \omega $, 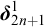 $\boldsymbol {\delta }^1_{2n + 1}$ satisfies the countable length everywhere club uniformization.
$\boldsymbol {\delta }^1_{2n + 1}$ satisfies the countable length everywhere club uniformization.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic





