No CrossRef data available.
Article contents
Generalized reduction theorems for model-theoretic analogs of the class of coanalytic sets
Published online by Cambridge University Press: 12 March 2014
Abstract
Let 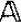 be an admissible set. A sentence of the form
be an admissible set. A sentence of the form 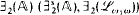 is a
is a 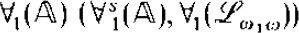 sentence if φ ∈
sentence if φ ∈ 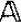 (φ is ∨ Φ where Φ is an
(φ is ∨ Φ where Φ is an 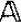 -r.e. set of sentences from
-r.e. set of sentences from 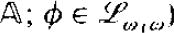 ). A sentence of the form
). A sentence of the form 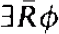 is an
is an 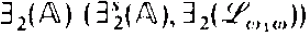 , sentence if φ is a
, sentence if φ is a 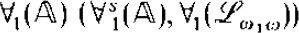 sentence. A class of structures is, for example, a ∀1
sentence. A class of structures is, for example, a ∀1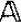 class if it is the class of models of a ∀1(
class if it is the class of models of a ∀1(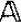 ) sentence. Thus ∀1(
) sentence. Thus ∀1(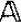 ) is a class of classes of structures, and so forth.
) is a class of classes of structures, and so forth.
Let 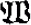 i, be the structure 〈i, <〉, for i > 0. Let Γ be a class of classes of structures. We say that a sequence J1, …, Ji,…, i < ω, of classes of structures is a Γ sequence if Ji ∈ Γ, i < ω, and there is I ∈ Γ such that
i, be the structure 〈i, <〉, for i > 0. Let Γ be a class of classes of structures. We say that a sequence J1, …, Ji,…, i < ω, of classes of structures is a Γ sequence if Ji ∈ Γ, i < ω, and there is I ∈ Γ such that 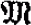 ∈ Ji, if and only if [
∈ Ji, if and only if [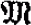 ],
],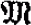 i, where [,] is the disjoint sum. A class Γ of classes of structures has the easy uniformization property if for every Γ sequence J1,…, Ji,…, i < ω, there is a Γ sequence J′t, …, J′i, …, i < ω, such that J′i ⊆ Ji, i < ω, ⋃J′i = ⋃Ji, and the J′i are pairwise disjoint. The easy uniformization property is an effective version of Kuratowski's generalized reduction property that is closely related to Moschovakis's (topological) easy uniformization property.
i, where [,] is the disjoint sum. A class Γ of classes of structures has the easy uniformization property if for every Γ sequence J1,…, Ji,…, i < ω, there is a Γ sequence J′t, …, J′i, …, i < ω, such that J′i ⊆ Ji, i < ω, ⋃J′i = ⋃Ji, and the J′i are pairwise disjoint. The easy uniformization property is an effective version of Kuratowski's generalized reduction property that is closely related to Moschovakis's (topological) easy uniformization property.
We show over countable structures that ∀1(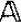 ) and ∃2(
) and ∃2(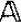 ) have the easy uniformization property if
) have the easy uniformization property if 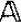 is a countable admissible set with an infinite member, that
is a countable admissible set with an infinite member, that 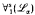 and
and 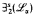 have the easy uniformization property if α is countable, admissible, and not weakly stable, and that
have the easy uniformization property if α is countable, admissible, and not weakly stable, and that 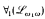 and
and 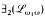 have the easy uniformization properly. The results proved are more general. The result for
have the easy uniformization properly. The results proved are more general. The result for 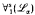 answers a question of Vaught(1980).
answers a question of Vaught(1980).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1993




