Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-06-09T20:20:29.358Z Has data issue: false hasContentIssue false
  • English
  • Français

A hierarchy of families of recursively enumerable degrees12

Published online by Cambridge University Press:  12 March 2014

Lawrence V. Welch
Lawrence V. Welch*
Affiliation:
Western Illinois University, Macomb, Illinois 61455
Get access Rights & Permissions [Opens in a new window]

Extract

Certain investigations have been made concerning the nature of classes of recursively enumerable sets, and the relation of such classes to the recursively enumerable indices of their sets. For instance, a theorem of Rice [3, Theorem XIV(a), p. 324] states that if A is the complete set of indices for a class of recursively enumerable sets (that is, if there is a class 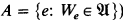of recursively enumerable sets such that 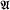and if A is recursive, then either A = ⌀ or A = ω. A relate theorem by Rice and Shapiro [3, Theorem XIV(b), p. 324] can be stated as follows:

Let 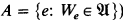be a class of recursively enumerable sets, and let A be the complete set of indices for 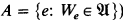. Then A is r.e. if and only if there is an r.e. set D of canonical indices of finite sets Du, u ∈ D, such that

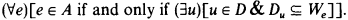
A somewhat similar theorem of Yates is the following: Let 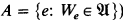be a class of recursively enumerable sets which contains all finite sets. Let A be the complete set of indices for 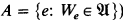. Then there is a uniform recursive enumeration of the sets in 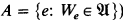if and only if A is recursively enumerable in 0(2)—that is, if and only if A is Σ3. A corollary of this is that if C is any r.e. set such that C(2)≡T⌀(2), there is a uniform recursive enumeration of all sets We such that We ≤TC [9, Theorem 9, p. 265].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 4 , December 1984 , pp. 1160 - 1170
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

The results in this paper are taken from the author's Ph.D. thesis, which was written at the University of Illinois at Urbana-Champaign under the guidance of Professor Carl G. Jockusch. The paper was written at Western Illinois University.

2

I would like to thank the referee for several valuable suggestions.

References

REFERENCES

[1]Lachlan, A. H., The priority method for the construction of recursively enumerable sets, Cambridge summer school in mathematical logic (Cambridge, England, 1971), Lecture Notes in Mathematics, vol. 337, Springer-Verlag, Berlin and New York, 1973, pp. 299–310.CrossRefGoogle Scholar
[2]Robinson, Robert W., Interpolation and embedding in the recursively enumerable degrees, Annals of Mathematics, ser. 2, vol. 93 (1971), pp. 285–314.CrossRefGoogle Scholar
[3]Rogers, Hartley Jr., Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[4]Sacks, Gerald E., Degrees of unsolvability, 2nd ed., Annals of Mathematics Studies, no. 55, Princeton University Press, Princeton, New Jersey, 1966.Google Scholar
[5]Shoenfield, Joseph R., Degrees of unsolvability, North-Holland, Amsterdam, 1971.Google Scholar
[6]Soare, Robert I., The infinite injury priority method, this Journal, vol. 41 (1976), pp. 513–530.Google Scholar
[7]Welch, Lawrence V., A hierarchy of families of recursively enumerable degrees and a theorem on bounding minimal pairs, Ph.D. thesis, University of Illinois, Urbana-Champaign, Illinois, 1981, chaps. 2, 3.Google Scholar
[8]Yates, C. E. M., On the degrees of index sets, Transactions of the American Mathematical Society, vol. 121 (1966), pp. 309–328.CrossRefGoogle Scholar
[9]Yates, C. E. M., On the degrees of index sets. II, Transactions of the American Mathematical Society, vol. 135 (1969), pp 249–266.CrossRefGoogle Scholar