Hostname: page-component-848d4c4894-p2v8j Total loading time: 0.001 Render date: 2024-06-01T04:06:09.824Z Has data issue: false hasContentIssue false
  • English
  • Français

HYBRID PARTIAL TYPE THEORY

Part of: General logic

Published online by Cambridge University Press:  29 May 2023

MARÍA MANZANO ,
ANTONIA HUERTAS Open the ORCID record for ANTONIA HUERTAS [Opens in a new window] ,
PATRICK BLACKBURN Open the ORCID record for PATRICK BLACKBURN [Opens in a new window] ,
MANUEL MARTINS Open the ORCID record for MANUEL MARTINS [Opens in a new window]  and
VÍCTOR ARANDA Open the ORCID record for VÍCTOR ARANDA [Opens in a new window]
MARÍA MANZANO
Affiliation:
DEPARTMENT OF PHILOSOPHY, LOGIC AND AESTHETICS UNIVERSITY OF SALAMANCA EDIFICIO FES. CAMPUS MIGUEL DE UNAMUNO AVDA. FRANCISCO TOMÁS Y VALIENTE, S/N 37007 SALAMANCA, SPAIN E-mail: mara@usal.es
ANTONIA HUERTAS
Affiliation:
FACULTY OF COMPUTER SCIENCE, MULTIMEDIA AND TELECOMMUNICATIONS UNIVERSITAT OBERTA DE CATALUNYA (UOC) RAMBLA POBLENOU, 156 08018 BARCELONA, SPAIN E-mail: mhuertass@uoc.edu
PATRICK BLACKBURN*
Affiliation:
SECTION FOR PHILOSOPHY AND SCIENCE STUDIES ROSKILDE UNIVERSITY (RUC), UNIVERSITETSVEJ 1 4000-DK ROSKILDE DENMARK
MANUEL MARTINS
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF AVEIRO, CAMPUS UNIVERSITÁRIO DE SANTIAGO 3810 193 AVEIRO, PORTUGAL E-mail: martins@ua.pt
VÍCTOR ARANDA
Affiliation:
DEPARTMENT OF LOGIC AND THEORETICAL PHILOSOPHY COMPLUTENSE UNIVERSITY OF MADRID, CIUDAD UNIVERSITARIA CALLE DEL PROF. ARANGUREN, 1 28040 MADRID, SPAIN E-mail: vicarand@ucm.es
*
E-mail: patrick.rowan.blackburn@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we define a logical system called Hybrid Partial Type Theory (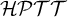$\mathcal {HPTT}$). The system is obtained by combining William Farmer’s partial type theory with a strong form of hybrid logic. William Farmer’s system is a version of Church’s theory of types which allows terms to be non-denoting; hybrid logic is a version of modal logic in which it is possible to name worlds and evaluate expressions with respect to particular worlds. We motivate this combination of ideas in the introduction, and devote the rest of the article to defining, axiomatising, and proving a completeness result for $\mathcal {HPTT}$.

Keywords

type theorypartial logichybrid logichigher-order modal logicrigidityexistencedenotationHenkin proofs

MSC classification

Secondary: 03B45: Modal logic (including the logic of norms)
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 43
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aranda, V., Huertas, A., Manzano, M., and Martins, M., On the philosophy and mathematics of hybrid partial type theory, forthcoming; Springer’s “Outstanding Contributions to Logic” series, volume in honor of Walter Carnelli.Google Scholar
Areces, C., Blackburn, P., Huertas, A., and Manzano, M., Completeness in hybrid type theory . Journal of Philosophical Logic , vol. 43 (2014), pp. 209–238.CrossRefGoogle Scholar
Areces, C., Blackburn, P., Manzano, M., and Huertas, A., Hybrid type theory: A quartet in four movements . Principia: An International Journal of Epistemology , vol. 15 (2011), no. 2, pp. 225–247.Google Scholar
Areces, C. and ten Cate, B., Hybrid logic , Handbook of Modal Logic (Blackburn, P., van Benthem, J., and Wolter, F., editors), Elsevier, Amsterdam, 2007, pp. 821–868.CrossRefGoogle Scholar
Blackburn, P., Representation, reasoning, and relational structures: A hybrid logic manifesto . Logic Journal of the IGPL , vol. 8 (2000), no. 3, pp. 339–365.CrossRefGoogle Scholar
Blackburn, P., Huertas, A., Manzano, M., and Jørgensen, K. F., Henkin and hybrid logic , The Life and Work of Leon Henkin (Manzano, M., Sain, I., and Alonso, E., editors), Springer, Cham, 2014.Google Scholar
Blackburn, P., Martins, M., Manzano, M., and Huertas, A., Exorcising the phantom zone . Information and Computation , vol. 287 (2022), p. 104754.CrossRefGoogle Scholar
Blackburn, P. and ten Cate, B., Pure extensions, proof rules, and hybrid axiomatics . Studia Logica , vol. 84 (2006), pp. 277–322.CrossRefGoogle Scholar
Church, A., A formulation of the simple theory of types, this Journal, vol. 5 (1940), no. 2, pp. 56–68.Google Scholar
Farmer, W. M., A partial functions version of Church’s simple theory of types, this Journal, vol. 55 (1990), no. 3, pp. 1269–1291.Google Scholar
Farmer, W. M., Andrews’ type system with undefinedness , Reasoning in Simple Type Theory: Festschrift in Honor of Peter B: Andrews on his 70th Birthday (Benzmueller, C., Brown, C. E., and Siekmann, J., editors), Studies in Logic, College Publications, London, 2008, pp. 223–242.Google Scholar
Farmer, W. M., Andrews’ type theory with undefinedness, preprint, 2014, arXiv:1406.7492.Google Scholar
Fitting, M., Types, Tableaus, and Gödel’s God , Kluwer Academic, Dordrecht, 2002.CrossRefGoogle Scholar
Fitting, M. and Mendelsohn, R., First-Order Modal Logic , Springer, Dordrecht, 1998.CrossRefGoogle Scholar
Gallin, D., Intensional and Higher-Order Modal Logic , North-Holland, Amsterdam, 1975.Google Scholar
Henkin, L., Completeness in the theory of types, this Journal, vol. 15 (1950), no. 2, pp. 81–91.Google Scholar
Henkin, L., A theory of propositional types . Fundamenta Mathematicae , vol. 52 (1963), pp. 323–334.CrossRefGoogle Scholar
Indrzejczak, A., Modal hybrid logic . Logic and Logical Philosophy , vol. 16 (2007), nos. 2–3, pp. 147–257.CrossRefGoogle Scholar
Manzano, M., Martins, M., and Huertas, A., Completeness in equational hybrid propositional type theory . Studia Logica , vol. 107 (2019), pp. 1159–1198.CrossRefGoogle Scholar