In this note we investigate an extension of Peano arithmetic which arises from adjoining generalized quantifiers to first-order logic. Markwald [2] first studied the definability properties of L1, the language of first-order arithmetic, L, with the additional quantifer Ux which denotes “there are infinitely many x such that…. Note that Ux is the same thing as the Keisler quantifier Qx in the ℵ0 interpretation.

We consider L2, which is L together with the ℵ0 interpretation of the Magidor-Malitz quantifier Q2xy which denotes “there is an infinite set X such that for distinct x, y ∈ X …”. In [1] Magidor and Malitz presented an axiom system for languages which arise from adding Q2 to a first-order language. They proved that the axioms are valid in every regular interpretation, and, assuming ◊ω1, that the axioms are complete in the ℵ1 interpretation.

If we let 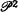denote Peano arithmetic in L2 with induction for L2 formulas and the Magidor-Malitz axioms as logical axioms, we show that in 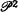we can give a truth definition for first-order Peano arithmetic, 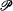. Consequently we can prove in 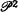that 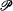is Πn sound for every n, thus in 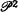we can prove the Paris-Harrington combinatorial principle and the higher-order analogues due to Schlipf.