Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-02T08:41:19.447Z Has data issue: false hasContentIssue false
  • English
  • Français

Provably total functions of intuitionistic bounded arithmetic

Published online by Cambridge University Press:  12 March 2014

Victor Harnik
Victor Harnik*
Affiliation:
Department of Mathematics, University of Haifa, 31999 Haifa, Israel, E-mail: rmsa302@haifauvm.bitnet
Get access Rights & Permissions [Opens in a new window]

Extract

This note deals with a proof-theoretic characterisation of certain complexity classes of functions in fragments of intuitionistic bounded arithmetic. In this Introduction we survey the background and state our main result.

We follow Buss [B1] and consider a language for arithmetic whose nonlogical symbols are 0, S (the successor operation Sx = x + 1), +, ·, ∣ ∣ (∣x∣ being the number of digits in the binary notation for x), 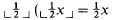rounded down to the nearest integer), # (x#y = 2∣x∣∣y∣) and ≤. We define 1 = S0, 2 = S1, s0x = 2x and s1x = 2x + 1. In Buss's approach the functions s0 and s1 play a special role. Notice that six is the number obtained from x by suffixing the digit i to its binary representation, and thus the natural numbers are generated from 0 by repeated applications of the operations s0 and s1. This means that they satisfy the induction scheme

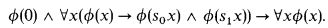
Using the fact that 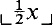is x with its last binary digit deleted, this can be stated more compactly in the following form, called by Buss the polynomial induction or PIND schema:

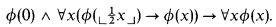
Buss defined a theory S2 consisting of a finite set BASIC of open axioms and the PIND-schema restricted to bounded formulas ϕ. The topic of bounded arithmetic is concerned with S2 and its fragments.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 2 , June 1992 , pp. 466 - 477
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B1]Buss, S. R., Bounded arithmetic, Bibliopolis, Napoli, 1986.Google Scholar
[B2]Buss, S. R., The polynomial hierarchy and intuitionistic bounded arithmetic, Structure in complexity theory, Lecture Notes in Computer Science, vol. 223, Springer-Verlag, Berlin, 1986, pp. 77–103.CrossRefGoogle Scholar
[CT]Clote, P. and Takeuti, G., Exponential time and bounded arithmetic, Structure in complexity theory, Lecture Notes in Computer Science, vol. 223, Springer-Verlag, Berlin, 1986, pp. 125–143.CrossRefGoogle Scholar
[C]Cook, S. A., Feasibly constructive proofs and the propositional calculus, Proceedings of the 7th ACM symposium on the theory of computation, 1975, pp. 83–97.Google Scholar
[CU]Cook, S. and Urquhart, A., Functional interpretations of feasibly constructive arithmetic, Annals of Pure and Applied Logic (to appear).Google Scholar
[G]Gödel, K., Uber eine bisher noch nicht benützte Erweiterung des finiten Standpunktes, Dialectica, vol. 12 (1958), pp. 280–287; English translation, Journal of Philosophical Logic, vol. 9 (1980), pp. 133–142.CrossRefGoogle Scholar
[KPT]Krajíček, J., Pudlák, P. and Takeuti, G., Bounded arithmetic and the polynomial hierarchy, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 143Ά#x2013;153.CrossRefGoogle Scholar