Hostname: page-component-848d4c4894-wg55d Total loading time: 0 Render date: 2024-06-13T04:54:36.900Z Has data issue: false hasContentIssue false
  • English
  • Français

HAUSDORFF DIMENSION FOR THE SET OF POINTS CONNECTED WITH THE GENERALIZED JARNÍK–BESICOVITCH SET

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Classical measure theory Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  07 December 2020

AYREENA BAKHTAWAR
AYREENA BAKHTAWAR*
Affiliation:
Department of Mathematics and Statistics, La Trobe University, PO Box 199, Bendigo, Victoria 3552, Australia e-mail: a.bakhtawar@latrobe.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we aim to investigate the Hausdorff dimension of the set of points 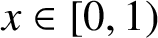$x \in [0,1)$ such that for any 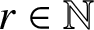$r\in \mathbb {N}$ ,

$$ \begin{align*} a_{n+1}(x)a_{n+2}(x)\cdots a_{n+r}(x)\geq e^{\tau(x)(h(x)+\cdots+h(T^{n-1}(x)))} \end{align*} $$
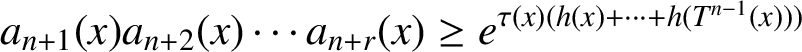
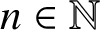holds for infinitely many $n\in \mathbb {N}$ , where h and 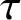$\tau $ are positive continuous functions, T is the Gauss map and 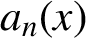$a_{n}(x)$ denotes the nth partial quotient of x in its continued fraction expansion. By appropriate choices of 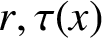$r,\tau (x)$ and 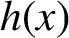$h(x)$ we obtain various classical results including the famous Jarník–Besicovitch theorem.

Keywords

continued fractionsHausdorff dimensionJarník–Besicovitch theorem

MSC classification

Primary: 11K50: Metric theory of continued fractions
Secondary: 11J70: Continued fractions and generalizations 11J83: Metric theory 28A78: Hausdorff and packing measures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 1 , February 2022 , pp. 1 - 29
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Dzmitry Badziahin

This research was supported by a La Trobe University Postgraduate Research Award.

References

Bakhtawar, A., Bos, P. and Hussain, M., ‘The sets of Dirichlet non-improvable numbers versus well-approximable numbers’, Ergod. Th. & Dynam. Sys. 40(12) (2020), 3217–3235.Google Scholar
Bakhtawar, A., Bos, P. and Hussain, M., ‘Hausdorff dimension of an exceptional set in the theory of continued fractions’, Nonlinearity 33(6) (2020), 2615–2640.CrossRefGoogle Scholar
Barral, J. and Seuret, S., ‘A localized Jarník–Besicovitch theorem’, Adv. Math. 226(4) (2011), 3191–3215.CrossRefGoogle Scholar
Besicovitch, A. S., ‘Sets of fractional dimensions (IV): on rational approximation to real numbers’, J. Lond. Math. Soc. 9(2) (1934), 126–131.CrossRefGoogle Scholar
Falconer, K., Fractal Geometry: Mathematical Foundations and Applications, 3rd edn (John Wiley, Chichester, 2014).Google Scholar
Hanus, P., Mauldin, R. D. and Urbański, M., ‘Thermodynamic formalism and multifractal analysis of conformal infinite iterated function systems’, Acta Math. Hungar. 96(1–2) (2002), 27–98.CrossRefGoogle Scholar
Huang, L., Wu, J. and Xu, J., ‘Metric properties of the product of consecutive partial quotients in continued fractions’, Israel J. Math. 238 (2020), 901–943.CrossRefGoogle Scholar
Hussain, M., Kleinbock, D., Wadleigh, N. and Wang, B.-W., ‘Hausdorff measure of sets of Dirichlet non-improvable numbers’, Mathematika 64(2) (2018), 502–518.CrossRefGoogle Scholar
Jarník, V., ‘Über die simultanen diophantischen Approximationen’, Math. Z. 33 (1931), 505–543.CrossRefGoogle Scholar
Khintchine, A. Y., Continued Fractions (Noordhoff, Groningen, 1963), translated by P. Wynn.Google Scholar
Kim, T. and Kim, W., ‘Hausdorff measure of sets of Dirichlet non-improvable affine forms’, Preprint, 2020, arXiv:2006.05727v2 [math.DS].Google Scholar
Kleinbock, D. and Wadleigh, N., ‘A zero–one law for improvements to Dirichlet’s theorem’, Proc. Amer. Math. Soc. 146(5) (2018), 1833–1844.CrossRefGoogle Scholar
Kleinbock, D. and Wadleigh, N., ‘An inhomogeneous Dirichlet theorem via shrinking targets’, Compos. Math. 155(7) (2019), 1402–1423.CrossRefGoogle Scholar
Kristensen, S., ‘Metric Diophantine approximation–from continued fractions to fractals’, in: Diophantine Analysis: Course Notes from a Summer School (ed. Steuding, J.) (Birkhäuser, Cham, 2016), Ch. 2, 61–127.CrossRefGoogle Scholar
Li, B., Wang, B.-W., Wu, J. and Xu, J., ‘The shrinking target problem in the dynamical system of continued fractions’, Proc. Lond. Math. Soc. (3) 108(1) (2014), 159–186.CrossRefGoogle Scholar
Mauldin, R. D. and Urbański, M., ‘Dimensions and measures in infinite iterated function systems’, Proc. Lond. Math. Soc. (3) 73(1) (1996), 105–154.CrossRefGoogle Scholar
Mauldin, R. D. and Urbański, M., ‘Conformal iterated function systems with applications to the geometry of continued fractions’, Trans. Amer. Math. Soc. 351(12) (1999), 4995–5025.CrossRefGoogle Scholar
Mauldin, R. D. and Urbański, M., Graph Directed Markov Systems: Geometry and Dynamics of Limit Sets, Cambridge Tracts in Mathematics, 148 (Cambridge University Press, Cambridge, UK, 2003).CrossRefGoogle Scholar
Walters, P., An Introduction to Ergodic Theory, Graduate Texts in Mathematics, 79 (Springer, New York, 1982).CrossRefGoogle Scholar
Wang, B.-W. and Wu, J., ‘Hausdorff dimension of certain sets arising in continued fraction expansions’, Adv. Math. 218(5) (2008), 1319–1339.CrossRefGoogle Scholar
Wang, B.-W., Wu, J. and Xu, J., ‘A generalization of the Jarník–Besicovitch theorem by continued fractions’, Ergod. Th. & Dynam. Sys. 36(4) (2016), 1278–1306.CrossRefGoogle Scholar