Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-06-10T10:40:53.563Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical Range of the Derivation of an Induced Operator

Part of: Basic linear algebra

Published online by Cambridge University Press:  09 April 2009

Randall R. Holmes ,
Chi-Kwong Li  and
Tin-Yau Tam
Randall R. Holmes
Affiliation:
Department of Mathematics and Statistics, Auburn University, Auburn, Alabama 36849-5310, USAholmerr@auburn.edu, tamtiny@auburn.edu
Chi-Kwong Li
Affiliation:
Department of Mathematics, College of William and Mary, PO Box 8795, Williamsburg, Virginia 23187-8795, USAckli@math.wm.edu
Tin-Yau Tam
Affiliation:
Department of Mathematics and Statistics, Auburn University, Auburn, Alabama 36849-5310, USAholmerr@auburn.edu, tamtiny@auburn.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let V be an n–dimensional inner product space over 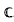, let H be a subgroup of the symmetric group on {l,…, m}, and let x: H → 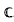be an irreducible character. Denote by 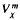(H) the symmetry class of tensors over V associated with H and x. Let K (T) ∈ End(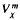(H)) be the operator induced by T ∈ End(V), and let DK(T) be the derivation operator of T. The decomposable numerical range W*(DK(T)) of DK(T) is a subset of the classical numerical range W(DK(T)) of DK(T). It is shown that there is a closed star-shaped subset 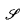of complex numbers such that

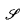⊆ W*(DK(T)) ⊆ W(DK(T)) = con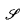

where conv 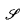denotes the convex hull of 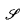. In many cases, the set 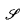is convex, and thus the set inclusions are actually equalities. Some consequences of the results and related topics are discussed.

Keywords

symmetry class of tensorsnumerical rangeinduced operatorderivationconvexity

MSC classification

Secondary: 15A69: Multilinear algebra, tensor products 15A42: Inequalities involving eigenvalues and eigenvectors
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 82 , Issue 3 , June 2007 , pp. 325 - 344
Copyright
Copyright © Australian Mathematical Society 2007

References

[1] Au-Yeung, Y. H. and Tsing, N. K., ‘Some theorems on the numerical range’, Linear Multilinear Algebra 15 (1984), 3–11.CrossRefGoogle Scholar
[2] Bebiano, N., Li, C. K. and Providencia, J. da, ‘Some results on the numerical range of a derivation’, SIAM J. Matrix Anal. Appl. 14 (1993), 1084–1095.CrossRefGoogle Scholar
[3] Bebiano, N., Li, C. K. and Providencia, J. da, ‘Generalized numerical ranges of permanental compounds arising from quantum systems of bosons’, Electron. J. Linear Algebra 7 (2000), 73–91.CrossRefGoogle Scholar
[4] Bhatia, R., Matrix Analysis (Springer, New York, 1997).CrossRefGoogle Scholar
[5] Djokovic, D. Z. and Tam, T. Y., ‘Some questions about semisimple Lie groups originating in matrix theory’, Canad. J. Math. 46 (2003), 332–343.CrossRefGoogle Scholar
[6] Goldberg, M. and Straus, E. G., ‘Elementary inclusion relations for generalized numerical ranges’, Linear Algebra and Appl. 18(1977), 1–24.CrossRefGoogle Scholar
[7] Halmos, P. R., A Hilbert Space Problem Book (Springer-Verlag, New York, 1978).Google Scholar
[8] Holmes, R. R., ‘Orthogonal bases of symmetrized tensor spaces’, Linear Multilinear Algebra 39 (1995), 241–243.CrossRefGoogle Scholar
[9] Holmes, R. R. and Tam, T. Y., ‘Symmetry classes of tensors associated with certain groups’, Linear Multilinear Algebra 32 (1992), 21–31.CrossRefGoogle Scholar
[10] Isaacs, I. M., Character Theory of Finite Croups (Academic Press, New York, 1976).Google Scholar
[11] James, G. and Kerber, A., The Representation Theory of the Symmetric Group, Encyclopedia of Mathematics and Its Applications, Volume 16 (Addison-Wesley Publishing Company, 1981).Google Scholar
[12] James, G. and Liebeck, M., Representations and Characters of Groups, Cambridge Mathematical Textbooks (Cambridge University Press, Cambridge, 1993).Google Scholar
[13] Li, C. K. and Tam, T. Y., ‘Operator properties of T and K(T)’, Linear Algebra and Appl. 401 (2005), 173–191.CrossRefGoogle Scholar
[14] Li, C. K. and Tsing, N. K., ‘The numerical range of derivations’, Linear Algebra and Appl. 119 (1989), 97–119.CrossRefGoogle Scholar
[15] Li, C. K. and Zaharia, A., ‘Decomposable numerical range on orthonormal decomposable tensors’, Linear Algebra and Appl. 308 (2000), 139–152.CrossRefGoogle Scholar
[16] Marcus, M., Finite Dimensional Multilinear Algebra, Part I (Marcel Dekker, New York, 1973).Google Scholar
[17] Marcus, M., Finite Dimensional Multilinear Algebra, Part II (Marcel Dekker, New York, 1975).Google Scholar
[18] Marcus, M., ‘Some combinatorial aspects of numerical range’, Second International Conference on Combinatorial Mathematis (New York) Ann. New York Acad. Sci. 319 (1979), 368–376.Google Scholar
[19] Marcus, M., ‘Ranges of derivations’, manuscript. 1989.Google Scholar
[20] Merris, R., Multilinear Algebra (Gordon and Breach Science Publishers, Amsterdam. 1997).CrossRefGoogle Scholar
[21] Poon, Y. T., ‘Another proof of a result of Westwick’, Linear Multilinear Algebra 9 (1980), 35–37.CrossRefGoogle Scholar
[22] Rockafellar, R. T., Convex Analysis (Princeton University Press, Princeton, 1970).CrossRefGoogle Scholar
[23] Tam, T. Y., ‘Convexity of generalized numerical range associated with a compact Lie group’, J. Austral. Math. Soc. 71 (2001), 1–10.Google Scholar
[24] Tsing, N. K., ‘On the shape of the generalized numerical ranges’, Linear Multilinear Algebra 10 (1981), 173–182.CrossRefGoogle Scholar
[25] Wang, B. Y., Foundation of Multilinear Algebra, (in Chinese) (Beijing Normal University Press, 1985).Google Scholar
[26] Wang, B. Y. and Gong, M. P., ‘A high symmetry class of tensors with an orthogonal basis of decomposable symmetrized tensors’, Linear Multilinear Algebra 30 (1991), 61–64.CrossRefGoogle Scholar
[27] Westwick, R., ‘A theorem on numerical range’, Linear Multilinear Algebra 2 (1975), 311–315.CrossRefGoogle Scholar